基于磁检测电阻抗成像技术的接地网成像重建研究*

黄明祥 卞宏志 林奕夫

（国网福建经济技术研究院 福州 350012）

1 引言

接地网是保证电力操作人员和运维人员安全至关重要的保障设施。当电网中存在雷电流和故障电流时，接地网可以提供放电通道［1］。因此，接地网的导电能力非常重要。随着运行时间的增加，由于腐蚀或分支断裂，接地网中会出现故障［2］，因此需要提高和完善测量接地网的拓扑和断点的技术。接地网通常由铜或铁导体制成，埋在地下约0.3m～2m 处。这导致通过常规方法直接测量断点或接地网拓扑很困难［3］。文献［4］将高频大电流的方波电流注入电网，通过对表面感应磁场强度的测量来研究接地网的完整性。文献［5］向下引线注入100A 直流电并测量表面磁场，基于电磁理论并借助测量结果来诊断接地网的断点。文献［6］向下引线注入300Hz的电流并测量表面磁场强度，并基于测量结果发出完整的接地网腐蚀或断点诊断检测系统。文献［7］采用电磁法诊断变电站接地网中的分支故障断裂。上述所有方法的思路都是通过直接测量磁场以检测接地网的拓扑或断点。但是，这些方法存在的共同问题是需要测量大量数据且计算工作复杂。磁检测电阻抗断层摄影（MDEIT）是用于重建对象电阻率分布的成像技术，最初用于重建人体的横截面电导率分布［8～9］。MDEIT 在技术上基于在对象内部生成电流分布并测量对象外部的磁场分布以重建成像对象的电阻率分布［10］。文献［11］从被检测物体的表面注入电流并测量物体周围的磁场，以重建内部电阻率分布。在该方法中，当前注入的点和测量点位于物体的表面中，这将限制注入点的数量和测量模式。因此，本文提出了一种基于MDEIT 的电阻率重建方法来确定接地网的拓扑和断点。本文描述了基于MDEIT 的接地网成像的正反问题。最后通过数值和实验例证实了该方法的可行性。

2 MDEIT中接地网的前向推导问题

2.1 前向推导问题的计算模型

本文的分析基于以下基本假设［12］：

1）当前场满足准静态条件。

2）成像对象内没有电流源。

3）成像对象的电阻率是各向同性的。

基于上述假设和麦克斯韦方程［13］，MDEIT中的前向问题可以简化如下：

其中式（1）满足：

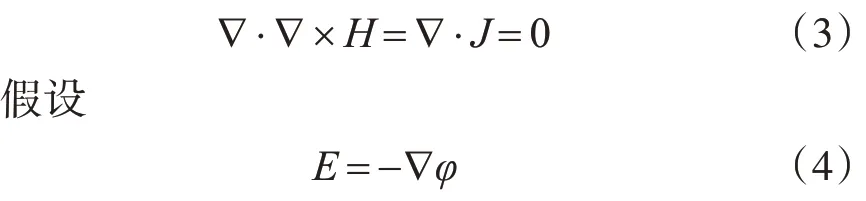
则式（3）可以改写为

其中σ是电导率。流入和流出边界面的条件如下：

其中n 是法向量，Jn是边界面的流入电流密度。假设边界面的电流密度是均匀的，Jn可以描述如下其中A+是当前电流流入面积，A-是当前电流流出面积。则式（6）可改写为

根据式（5）和（6），使用有限元方法（FEM）［14］来计算φ，则电流密度可以通过下式计算：

基于 Biot-Savart 定律［15］，磁通强度 B 可描述如下：

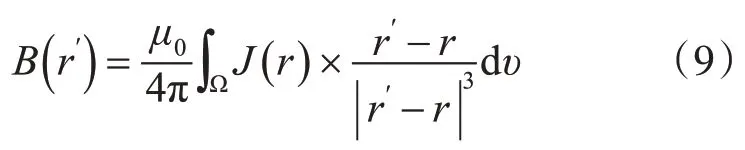
因此，MDEIT 的前向推导问题是在知道当前J和电导率σ时求解B。

2.2 计算方法

为了解决MDEIT 的前向问题，可以使用有限元方法求解式（5）和（8），并使用式（9）来分析MDEIT前向推导问题。式（5）用有限元方法可表述为

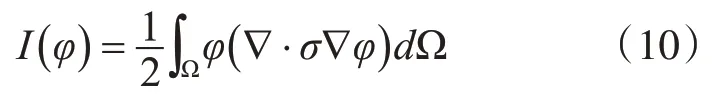
根据格林函数理论，式（10）可以改写为

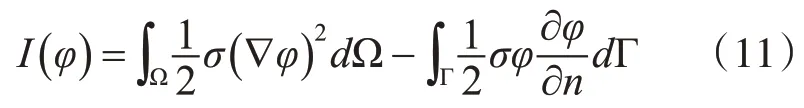
考虑到边界条件，上式改写为

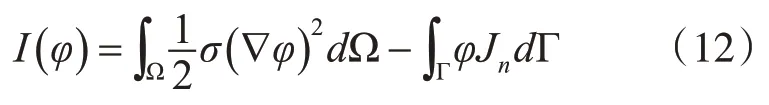
式（12）的最小化问题可表述为

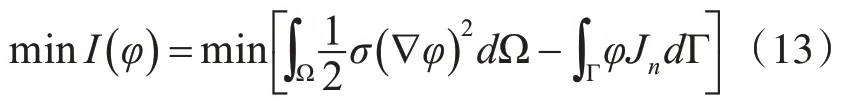
如果k是有限元中的单元数量，那么

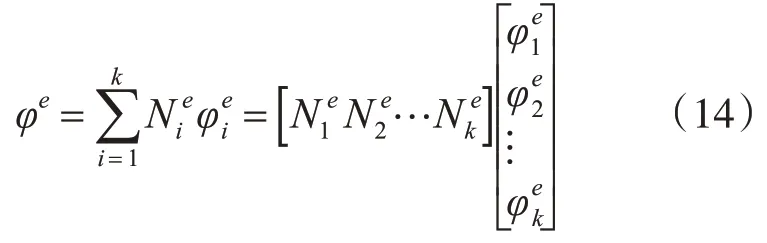
式（13）和（14）可改写为

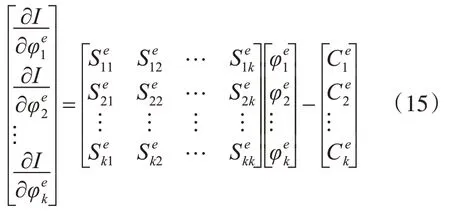
根据式（16），φ可以计算得出，然后J和B也可以分别用式（8）和（9）计算得出。

2.3 仿真算例

仿真案例研究了典型的方形接地网，接地网大小约为2m×2m，网格大小为1m×1m，如图1 所示。注入电流为10A，测量平面与接地网之间的垂直距离为h=0.8m。

基于有限元分析，接地网的网格模型如图2 所示。根据式（8），测量平面上的磁通密度如图3 所示。

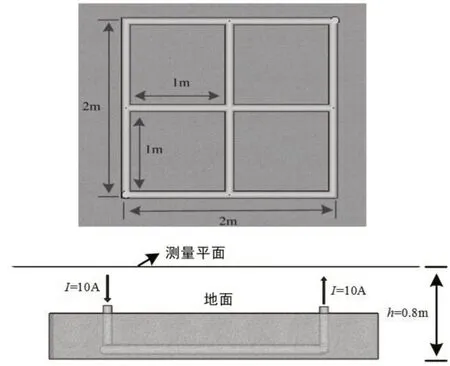
图1 简化的接地网格模型

图2 接地网的网格模型

从图3 中可以看出，当电流流过导体时，电流将在测量平面上产生磁通密度。

图3 测量平面上的磁通密度

3 MDEIT中接地网的后向推导问题

3.1 后向推导问题的计算模型

磁通密度和电阻率分布之间的关系如式（17）。 MDEIT 的反向问题是在知道B 时找到σ并重建电导率分布：

其中B 和σ是测量平面上的磁通密度和成像区域的电导率。为了求解式（16）中的σ，根据最小二乘法，可以得到目标函数如下：

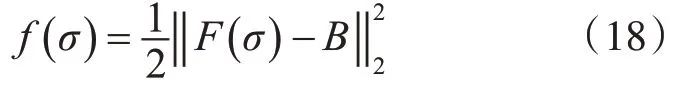
对式（17）求导：

式（19）中A 是雅可比矩阵。式（18）的泰勒级数 展 开 为其 中是海森矩阵，并且 ΔσK=σK+1-σK，

根据式（8）和（9），外部磁通密度B 和电导率σ分布矩阵之间的关系可以写成如下：

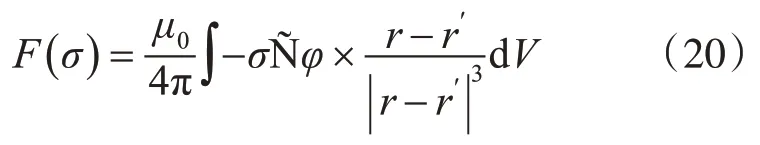
在重建过程中，电导率σ可以通过迭代方法计算，迭代方程如下：

电阻率δ可根据下式计算：

式（22）中δ和σ是分别电阻率和电导率。

3.2 仿真算例

基于图1 所示的模型，接地网的电阻率分布如图4 所示。红色区域和蓝色区域分别代表接地网的土壤和钢制接地体。

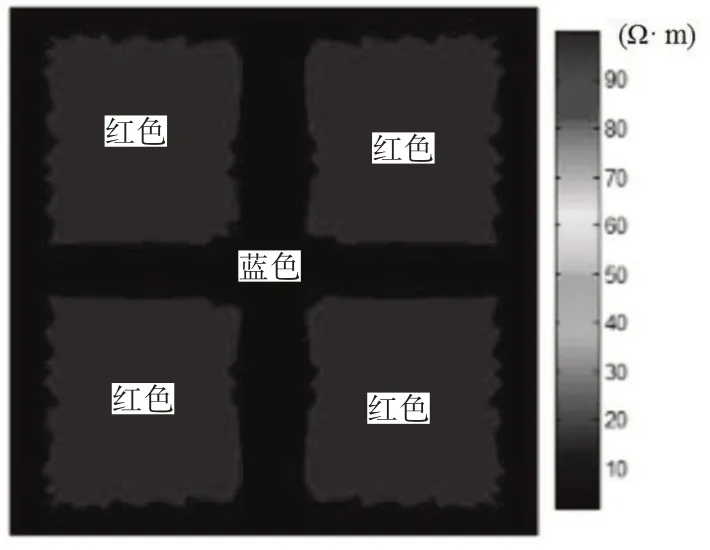
图4 接地网模型的电阻率分布

假设流入的电流为10A，则测量平面上的磁通密度B 可以被测量。基于所提出的方法，可以重建电阻率分布，如图5所示。

图5 表明，高电阻率区域主要集中在接地网的中心，此处主要是土壤，并具有与图4 类似的电阻率分布。该电阻率的重建结果表明该方法可用于测量接地网拓扑，以及测定地网中可能存在的断点。

图5 电阻率分布的重建结果

4 实验验证

如图6所示，实验所搭建的小型的接地网由2×2 方形网格组成，接地网的导体采用Ø3.5mm 铜软线。 为了重建接地网的电阻成像，霍尔效应探头和三维数控电机平台用于测量测量平面上的磁通密度。测量点的总数为100，点间距为1cm。测量探头在每个点的稳定时间是2s。实验平台如图7所示。

图6 实验所用接地网

图7 实验平台

根据本文提出的方法所重建的电阻率分布如图8所示。

可以看出，存在四个具有高电阻率的红色区域，这与预定义的实验条件一致此外，在存在断点情况下的电阻率分布如图9 所示，其中红色和蓝色区域分别代表土壤和接地网的导体。

图8 电阻率分布的重建结果

图9 接地网模型的电阻率分布

相应的电阻率重建结果如图10 所示。可以看出，有三个具有高电阻率的红色区域，这与图9 中的预定电阻率分布相匹配。可以得出结论，所提出的方法可用于测量通过重建接地网的成像来确定接地网的拓扑结构和断点。

图10 电阻率分布的重建结果

5 结语

本文提出了一种基于MDEIT 的接地网电阻率重建方法。首先分析了基于MDEIT 的接地网成像的正反向推导问题。然后，通过数值和实验例验证了所提方法的可行性。实验结果表明电阻率重建方法可用于测量接地网的拓扑和断点。