基于面板数据灰色关联分析的城市创新能力评估——以长三角城市群为例

席崇俊 刘志辉 杨 岩

（中国科学技术信息研究所，北京 100038）

0 引言

创新能力的概念是由Burns和Stalker于1961年首次提出，主要用来反映企业利用新技术生产新产品的能力，随着后续研究的不断深入，创新能力的范围也逐渐延伸至城市和国家层面上[1]。城市创新能力是指一个城市将知识、技术等各种创新要素转化成为新产品、新工艺和新服务的能力，综合反映了该城市的知识、技术、文化、制度等发展状况[2]，是城市核心竞争力的重要体现[3]。对城市的创新能力进行综合评价，可以很好地了解该城市的创新状况，洞悉城市创新中的优势与劣势，从而为建设创新型城市与实施区域协调发展战略提供帮助[4]。

（1）城市创新能力评估体系的研究现状。关于创新能力评价指标体系的研究最早开始于国外。2000年，欧洲理事会首次制定了欧盟创新记分牌，该记分牌由投入、产出、活动等3 个一级指标，8 个二级指标和24 个三级指标构成，用于评价各国的创新绩效[5]。随后，Charles Landry[6]提出了包括创新资源和创新活力两个方面的较为完善的城市创新能力评价指标体系。Porter等[7]提出了从科研人才比重、创新政策、创新环境、产业集群等方面构建城市的创新指数评价指标体系。Richard Florida[8]提出了由才能（Talent）、技术（Technology）和容忍度（Tolerance）组成的3T创新指数。Augusto López-Claros等[9]提出了由制度环境、人力资本、监管框架、研发、信息利用等构建了国家创新能力指数。美国波士顿企业咨询管理公司（BCG）联合美国NAM构建了包含5 个创新投入指标和2 个创新产出指标的全球创新指数[10]。针对中国国情，国内学者也构建了相应的创新能力评价指标体系，大致可以分为三类:一是从城市创新对象的技术、制度、政策以及环境等层面构建相应的评价指标体系；二是根据城市创新系统中投入与产出的过程建立评价指标体系；三是对前两类的综合，以城市创新对象中的创新过程来构建评价指标体系[11]。黄继等[12]从城市创新系统中的搜寻能力、探索能力、选择能力出发，根据创新投入、转化、产出的过程构建了城市创新系统评价指标体系。杨华峰等[13]结合国内外研究成果从知识、技术、服务、文化、制度等方面选取了16 项指标构建评价体系。王仁祥等[14]和杨志兵等[15]从投入、过程、环境和产出4 个因素出发选取了29 项指标来反映城市的创新能力。周纳[16]则在此基础之上加入了创新资源、创新机制和创新绩效等指标。谢攀[17]认为，创新环境是创新能力的保障，因此将创新环境的支撑能力纳入指标体系。余正娟[18]认为，随着互联网时代的来临，城市的网络发展程度和运行能力受到高度重视。

（2）城市创新能力评估方法的研究现状。对于城市创新能力评估方法的研究，不同学者从不同角度提出了不同的方法。段利忠等[2]从知识、技术、制度、服务等方面的创新能力出发，用灰色聚类分析法对我国东部具有代表性的12 个城市创新能力进行了聚类分析。王保乾等[19]运用超效率DEA-CCR模型和双重差分法测算了创新城市的创新绩效，分析了城市创新绩效的影响因素，并评价了创新型城市建设对于城市创新绩效的实际效果。郭华巍[20]从城市的创新投入、创新环境和创新产出3 个方面利用结构方程模型对城市的创新能力进行了分析。侯仁勇等[21]运用主成分分析法对国内5 个城市的创新能力进行了六维指标评价分析。郭华巍[22]从城市创新的主体、对象、过程出发，建立了SOP模型，并据此构建一个城市创新能力的基本评价指标体系。曹杨等[23]根据耗散结构理论，设计了城市创新系统评价指标体系，并采用网络层次分析法（ANP）计算各评价指标的权重。秦广虎等[24]从城市创新投入水平、创新产出水平、创新支撑能力与反馈能力出发，利用级数突变理论构建城市综合创新力评价指标体系，并对国内6 个省会城市的创新能力进行了实证分析。杜娟等[25]利用数据包络分析模型，从共享投入和分阶段产出两阶段出发，对国内52 个重点城市的创新能力进行了总体和单阶段评估。李斌等[26]采用熵值法、基尼系数、探索性空间统计分析等方法从时间、空间两个维度对2007—2016年我国35 个大中城市创新能力的评价、时空格局与演化规律进行了可视化分析。

综上所述，从国内外创新能力评估的相关研究现状中可以看出，国外研究侧重于对创新能力评估指标的研究，而国内则侧重于对方法的探讨，本文也主要从方法层面上对城市创新能力进行评估。目前对于城市创新能力评估的方法主要有多元统计分析、数据包络分析和指数分析等方法。这些方法大多都是基于时间序列和截面数据进行研究的，难以从动态视角全面考察城市的创新能力。在城市创新能力评估中，样本数据刻画的是某个时间节点内的信息，常常是一个“净增量”，单独考察每个数据的特征或者用折线将数据点简单相连，或多或少都会影响评估的准确性。此外，城市的创新活动中存在时间滞后性，创新投入后并不会立刻得到创新产出，某些指标不仅受到同期因素的影响，而且受到历史因素的影响。

而灰色关联分析不受样本数量以及样本规律是否明显的影响，因此被广泛采用。本文将选择面板数据对城市创新能力进行灰色关联分析。在构建城市创新能力评价指标体系的基础上，对城市创新能力面板数据进行累加生成，并将生成后的面板数据映射成空间中的网状曲面，再利用灰色关联分析对曲面间的相似程度和接近程度进行研究，以此表征城市之间的创新发展速度与创新能力水平，从而对城市的创新能力进行综合评估。

1 基于面板数据的灰色关联分析方法

灰色关联分析方法是由邓聚龙教授在1985年首次提出的，弥补了数理统计方法分析时所导致的缺憾。灰色关联度分析对一个系统发展变化态势提供了量化的度量，适合动态历程分析。因此，无论是样本量多少还是样本有无明细规律，灰色关联度分析方法都可对数据的发展趋势进行分析，而且计算量不大，方便快捷[27]。相比于时间序列数据和横截面数据而言，面板数据提供了个体的动态行为信息，可以解决单个时间序列数据和截面数据所不能解决的问题。

1.1 累加生成算子与灰色信息挖掘

累加生成是使数据由灰变白的一种方法，通过累加可以挖掘数据积累过程的演变趋势，从而发现原始数据中所蕴含的某些特性或规律[27]。比如创新投入水平，若按单个年份看，可能没有什么规律，若将每年的投入进行累加，则规律非常显著。对非负样本数据进行累加生成后，都会减少随机性，呈现出近似指数增长的规律，样本数据越光滑，生成后的指数规律也就越明显。

1.2 面板数据的矩阵表示与几何特征

面板数据是将横截面数据和时间序列数据相结合起来的一种数据类型，它同时包含对象维、指标维、时间维3 个维度。时间序列数据可以用一组向量表示，横截面数据可以用一个矩阵表示，因此面板数据可以在横截面数据的基础上用多个矩阵表示。构成面板数据的矩阵可以按对象维、指标维、时间维分成对象行为矩阵、指标行为矩阵、时间行为矩阵。本文将以对象行为矩阵进行研究。

定义1 设有N座城市、M项创新指标、T个观测时刻，记第i座城市（i=1,2,…,N）第s项创新指标（s=1,2,…,M）在t时刻（t=1,2,…,T）的观测值为xi(s,t)，则城市i的行为矩阵是

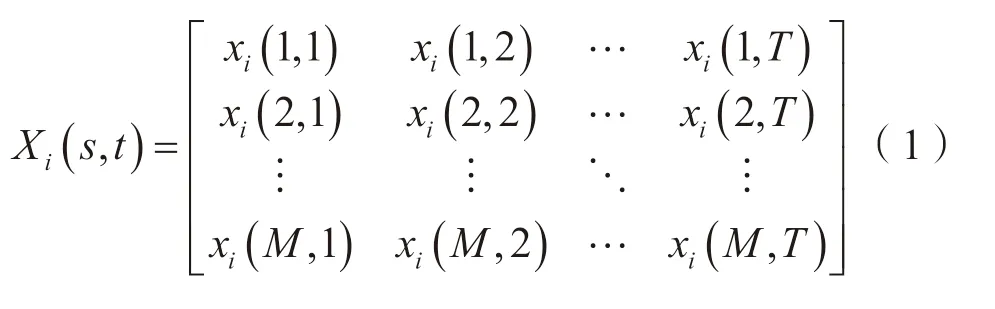
城市创新面板数据可以表示为

对于经累加算子作用后的城市创新面板数据，将其映射成三维空间中的若干个离散点，并将这些离散数据点看作网状结构的节点，分别对指标维和时间维的序列节点进行数据拟合，从而得到若干条相互交织的拟合曲线，城市创新面板数据便可投射为三维空间中的若干张曲面网格。因此，可以通过研究曲面网格之间的几何特征对城市的创新能力进行评估。

2 城市创新能力评估模型构建及评估方法

2.1 城市创新发展速度模型构建

一个城市的创新发展速度可以表现为对应曲面网格的形状，因此可以通过对曲面网格形状上的相似性研究评估城市之间的创新发展速度。而曲面网格的相似性又可以转化为分析若干条拟合曲线的相似性，计算对应拟合曲线的相似关联系数，再取算术平均值作为曲面网格的灰色相似关联度。本文仅考虑非负平衡创新面板数据，数据序列均为1-时序且等长，并假设拟合曲线的拐点仅出现在节点处。首先将几何中刻画曲线段平均弯曲程度的平均曲率应用到数据序列的拟合曲线段中，得到相应的平均曲率公式。为准确度量拟合曲线段的形状，降低曲线凹凸性的影响，按时序将一个拟合曲线段分成若干条小曲线段进行研究，并假设每条小曲线段的凹凸性不变。

定义2 设城市i在某一指标下时间序列为

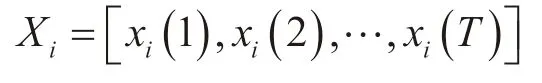
该时间序列的拟合曲线为fi(x),x∈[1,T]，则fi(x)被区间[k,k+1]分成了若干条小曲线段，其中k=1,2,…,T-1，则小曲线段fi(k,k+1)的平均曲率是

通过对应小曲线段之间的平均曲率大小关系，可以分析这些小曲线段之间的相似程度。在此采用灰色T型关联度公式计算相似关联系数，并规定当两个小曲线段的凹凸性一致时，关联系数为正，否则为负。取小曲线段相似系数的算术平均值来代表整个曲线段之间的相似程度。对于城市创新面板数据来说，这些曲线段分布在指标维和时间维，要分维度单独计算曲线段的相似关联度，并取两个维度相似关联度的算术平均值作为城市创新发展速度的相似关联度。

2.2 城市创新能力水平模型构建

城市创新评估除了要考察城市创新的发展速度，还要分析城市的创新能力水平，而城市创新能力的大小可以表现为对应的曲面网格所处的高低。通过对曲面网格在距离上的接近程度，可以考察城市创新能力水平的相似性。在对数据拟合的基础上，通过不同曲线段与坐标轴围成的面积差来刻画曲线段之间的接近程度，面积差越小则越接近。由于曲线段的凹凸性不会对其接近程度造成影响，因此可以对整个曲线段进行分析。

定义3 设城市i在某一指标下时间序列为

该时间序列的拟合曲线为

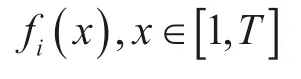
曲线段fi(x)与坐标轴所夹面积为

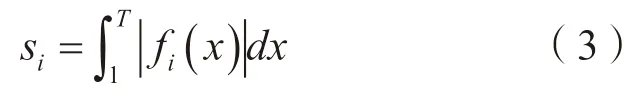
通过对应曲线段之间面积差的大小关系，可以分析这些曲线段之间的接近程度，这里采用灰色绝对关联度公式计算接近关联度。同样地，对于城市创新面板数据来说，接近关联度也分为指标维和时间维，取这两个维度接近关联度的算术平均值作为城市创新能力水平的接近关联度。

2.3 城市创新能力评估方法

根据城市创新发展速度的相似关联度和城市创新能力水平的接近关联度，取二者的算术平均值作为城市创新综合能力关联度，并进行城市创新能力的评估。城市创新能力评估有以下步骤。

步骤1:选取城市创新能力评估指标，构建城市创新面板数据，并选取每个指标下的最优值构建理想城市矩阵数据。

步骤2:对城市创新面板数据和理想城市矩阵数据进行累加生成，并对累加生成后的数据进行曲线拟合。

步骤3:分别计算各城市与理想城市之间的创新发展速度相似关联度、创新能力水平接近关联度和创新综合能力关联度。

步骤4:根据各城市之间的关联度大小进行城市创新能力评估。

3 实例分析

长三角城市群是我国经济发展最活跃、开放程度最高、创新能力最强的区域之一，在国家现代化建设大局和全方位开放格局中具有举足轻重的战略地位[28]。支撑和引领国家创新发展是长三角城市群的重要功能。作为我国创新发展高地，长三角城市群肩负着带领全国实现创新发展的重要使命。因此，本文选择长三角城市群进行分析评估城市创新能力。

3.1 指标构建及数据来源

本文参照相关文献对长三角城市群中27 座城市构建创新指标体系（表1）。由于部分指标的近几年数据难以获取，为了保证各指标数据的连续性与统一性，本文选取2011—2015年各城市相关指标数据，构建长三角城市创新能力面板数据。由于数据较多，此处不作展示，数据来源于2011—2015年各省市统计年鉴。

表1 长三角城市群创新指标体系

3.2 结果分析

多项式函数计算简单、易于分析、平整性强，对数据的拟合效果较好，因此本文基于多项式函数对数据序列进行曲线拟合。首先选取每个指标在各个观测时间下的最优值，构造理想城市矩阵数据，再分别将27 个待研究城市矩阵逐一与理想矩阵进行关联度计算。从表2可以看出，城市创新面板数据经累加操作前后的综合关联度计算结果有着明显不同，尤其是对城市创新投入与创新产出能力来说，经累加操作后的综合关联度的结果要低于不经累加操作的结果，说明对创新面板数据进行累加操作，确实可以放大数据的变化趋势，降低创新因时间滞后性带来的影响。

根据表3，分别从创新投入、创新环境、创新产出3 个方面具体分析长三角各城市的创新发展速度、创新能力水平和综合创新能力。

（1）创新投入能力评估。在长三角城市群中，上海市的创新投入水平和发展速度均较为突出，关联度值均为1，说明创新投入指标的最优值均选取于上海市。苏州市的创新投入能力综合关联度值为0.714，紧跟上海市之后，南京、杭州、宁波、无锡等城市的创新投入综合能力属于同一层次，但在创新投入水平和创新投入发展速度上仍有差距，其中无锡市创新投入的相似关联度和接近关联度分别为0.68 和0.618，表现稍弱。南通、合肥、常州等城市的相似关联度均在0.67左右，接近关联度在0.57 上下，说明这些城市正在不断增加创新投入，以提高其创新能力。铜陵、滁州、池州等城市的创新投入综合能力与除上海市外的其他城市差距不大，但是创新投入的水平则在长三角城市群中属于相对较弱的城市。

（2）创新环境能力评估。上海市创新环境能力的综合关联度为0.918，依然在长三角城市中较为突出，但并不是所有指标都是最优的。相比于各城市在创新投入能力上的表现，长三角城市的创新环境能力整体都比较高，各城市之间的差距较小，接近关联度最大值与最小值的差仅为0.198。南京市、杭州市、宁波市的创新环境综合能力属于同一层次，但杭州市的创新环境水平则表现稍佳，接近关联度为0.81。宣城、池州、滁州等城市的创新环境能力虽然在长三角城市中排名靠后，但是差距并不大。池州市的创新环境能力接近关联度，与除上海市、苏州市外的其他城市的最大差值也仅为0.057。

（3）创新产出能力评估。由于上海市的创新投入能力较为突出，因而其创新产出能力也较为突出，综合关联度值也达到了1，创新产出指标的最优值也均选取于上海。宁波、南通、常州等城市的创新产出相似关联度均在0.67 左右，说明它们的创新产出发展速度比较接近，均处于快速发展阶段，其中南通市的创新产出接近关联度为0.574，创新产出水平稍低于其他几个城市，但是创新产出的相似关联度为0.674，创新产出速度稍高于它们。安庆、宣城、池州等城市的创新产出速度与除上海市、苏州市外的其他城市差距不大，最大差值仅为0.024，创新产出的接近关联度在0.5 上下，创新产出水平在区域内相对较弱。

（4）综合创新能力评估。长三角城市群中，上海市的综合创新能力处于一枝独秀的地位，综合关联度为0.966，比第二名的苏州市高了近0.2。南京、杭州、宁波等城市的综合创新能力属于同一层次，综合关联度值在0.7 以上。滁州、池州、安庆、宣城等城市的创新能力综合关联度值在0.62 左右，相对较弱。各城市之间存在着明显的创新层次，但是综合创新能力整体上差距并不大，除上海市外的其他城市创新能力的综合关联度最大差值也仅为0.14。

表2 累加前后主要城市与理想矩阵的综合关联度

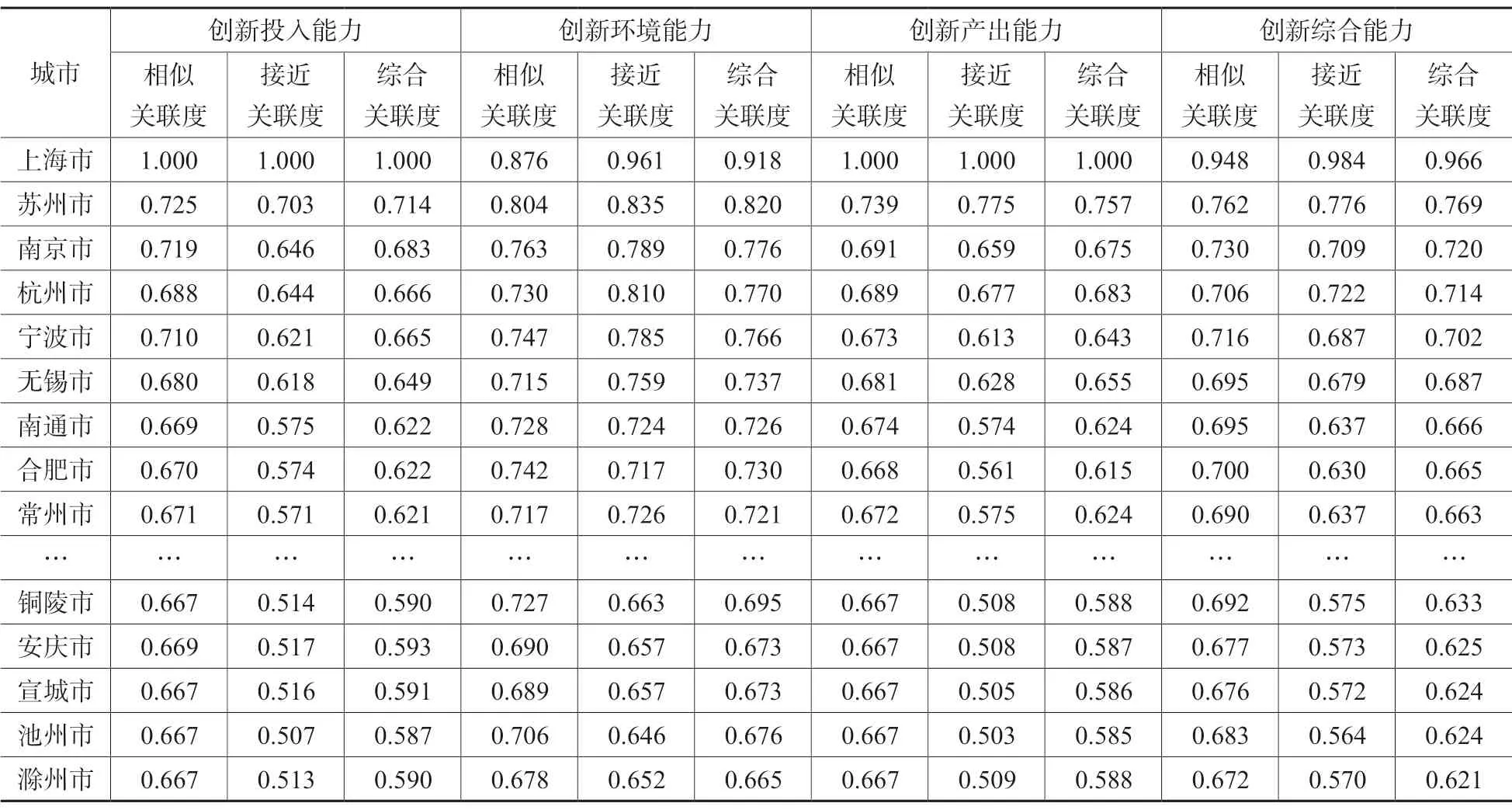
表3 累加后主要城市与理想矩阵的关联度

以累加后的结果为例，分别计算各指标下城市间相似关联度、接近关联度和综合关联度的均值、标准差、极差统计量（表4）。从表4可以看出，长三角城市创新能力的综合关联度均值为0.669、标准差为0.068，说明各城市的创新发展比较均衡，且处于一个较高水平，尤其是创新环境能力整体较优，均值达到了0.723，标准差和极差都非常小。综合创新能力的相似关联度均值为0.701、极差为0.276，说明长三角城市群的综合创新发展速度较快，且彼此间差距较小。此外，从创新投入和创新产出能力来看，接近关联度在这两个指标下的极差分别为0.493 和0.497，标准差也相对较高，说明各城市的创新投入和产出水平仍有差距，但是从相似关联度来看，均值分别为0.687 和0.685，说明各城市的创新投入与产出的发展速度齐头并进，相对稳定。

4 结语

本文首先基于面板数据利用灰色关联分析对城市创新能力进行评估，对现有灰色关联分析方法进行了优化，利用城市创新面板数据序列进行累加生成方法，放大数据的变化趋势。然后利用曲线对累加生成的序列进行拟合，通过计算拟合曲线的平均曲率以及与坐标轴所围的面积，从城市创新发展速度和创新能力水平角度，全面地分析城市的创新能力。最后将构建的城市创新能力评估模型应用于长三角城市的创新能力评估中，得出以下结论。

（1）长三角各城市的创新能力存在关联现象，创新能力较高和创新能力较低的城市在空间中都趋于集聚。创新能力较强的城市主要集中在上海市周边，而创新能力相对较弱的城市主要位于安徽省的西北部，远离沿海发展区域。综合创新能力整体上由沿海地区向内陆地区递减，但随着南京市、合肥市等内陆中心城市创新能力的提高，存在着空间溢出效应，创新能力呈现出向内陆城市扩散的趋势。

（2）长三角城市群中存在一些创新梯度，上海市是我国最大的经济中心，具有优越的创新基础，其创新能力较领先于其他城市，是长三角创新网络中的关键节点。苏州、南京、杭州等城市的综合创新能力在长三角城市群中属于领先地位。在综合创新能力排名前十的城市中，江苏省占了一半，涌现出一批以南京市、苏州市为代表的创新能力位于前列的城市，省内创新整体水平较高。就浙江省而言，各城市间综合创新能力存在着一定的差距，其中杭州市是引领浙江省创新驱动发展战略的主要引擎，也是长三角地区最具创新潜力的城市之一。在安徽省，仅有合肥市处于前列，省内其他城市的创新能力相对较弱。

（3）长三角各城市的综合创新能力差距不大，区域内城市创新环境整体水平较高，但在创新投入与创新产出能力方面则体现出分异性。区域内经济发展水平较高的城市，其创新投入和创新产出能力也相对较高，这类城市有着良好的创新环境与创新政策，往往更容易吸引人才、资金、企业等创新要素的集聚。而在创新投入与创新产出能力属于同一层次的城市里，各城市的发展速度和发展水平存在一定的差异性。

本文首先通过构建创新能力面板数据，从个体的动态发展视角全面考察城市的创新能力，弥补了单个时间序列数据和横截面数据难以解决的问题。然后通过对原始数据进行累加生成，可以减少创新活动中的时间滞后效应而产生的影响，并利用灰色关联模型从累加数据的发展趋势进行研究，降低了因样本量少和数据缺失而造成的误差。最后结合长三角城市群的创新指标数据进行实证分析，研究结果对长三角城市群的创新发展具有一定的借鉴意义。

表4 累加后的各指标关联度统计结果