不同海拔对车用散热器性能的影响分析

景 琦，骆清国，桂 勇，刘红彬

(陆军装甲兵学院车辆工程系，北京 100072)

全世界有许多高海拔公路和在高海拔作业的车辆，尤其在中国西部地区，高原、山地分布广阔。据统计，在中国海拔1 km以上的地区约占国土总面积的58%，海拔2 km以上的地区约占国土总面积的1/3，海拔3 km以上的高原地区约占全国总面积的26%，尤其是青藏高原地区，海拔高度普遍超过 3 km，超过600万辆机动车在这些地区行驶[1]。

在高原地区，海拔由0 m上升到5 000 m时，空气密度将下降41.7%，大气压力下降48.6%。恶劣的高原环境影响着机动车的动力性、经济性、起动性和排放性，同时也对车辆的冷却传热产生了诸多不利的影响。散热器作为车辆冷却传热的重要部件之一，受高原空气物性参数变化的影响较大，随着海拔的升高，散热器散热能力显著降低，导致发动机在高原工作时热负荷增大，而传统的散热器大多都是按照平原条件进行设计，忽略了海拔高度对散热器的影响。因此，开展不同海拔下散热器性能影响研究，对散热器设计及变海拔条件下的车辆热管理研究具有重要意义。

目前，对平原条件下散热器的性能规律研究较多，而高原环境下散热器相关研究较少。在已有的研究中，李毅等[2]通过数值计算的方法建立了不同翅片散热器的换热系数方程，并通过试验验证计算方法的可靠性；许翔等[3]采用热网络法，结合FlowMaster仿真软件，模拟出海拔高度、迎面风速及冷却液流量对散热器传热性能的影响；蔡惠坤等[4]利用MATLAB编写了管带式散热器计算程序，比较了多海拔下不同翅片的散热特性和风阻特性。

从上述文献可知，针对高原环境下散热器性能的三维仿真研究并不多见。因此，现利用Fluent软件对散热器在高原环境下的传热性能进行仿真，由于散热器翅片较多且结构复杂，直接划分网格所需计算量过大，将散热器翅片部分视作多孔介质，其参数通过对散热器单元进行计算流体力学(computational fluid dynamics，CFD)仿真得到，研究海拔高度、风速以及冷却水流量对散热器换热能力的影响规律，以期为散热器的高原传热计算和优化匹配提供技术参考。

1 高原空气热力学参数

在高原环境下，空气的密度、压力、温度和运动黏度等热力学参数受影响较大，相比之下，比热容、动力黏度、热导率等参数受环境变化影响较小[5]。温度随海拔高度的升高而下降，其对应关系为

TH=T0-0.006 5H

(1)

式(1)中：TH为海拔高度H处的温度；T0为平原空气温度；H为海拔高度。

大气压力与海拔高度的换算公式[6]为

pH=p0(1-0.022 57H)5.255 9

(2)

式(2)中：pH为海拔高度H处的大气压力；p0为标准大气压力。

根据式(1)、式(2)计算出不同海拔下空气的温度与压力，如表1所示。

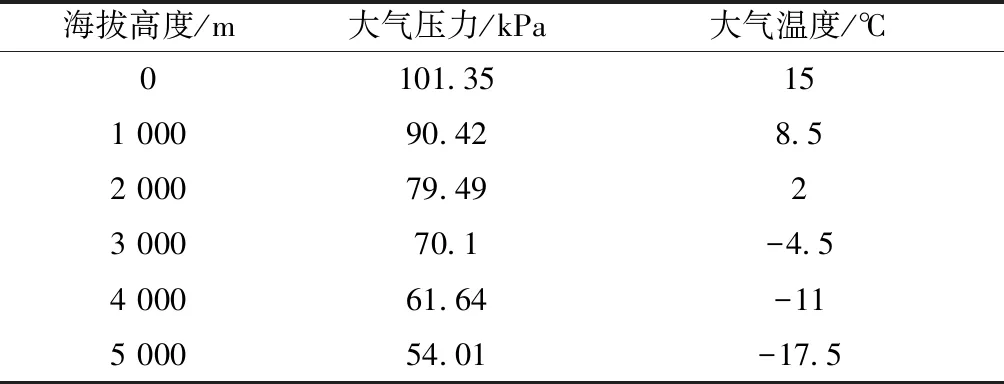
表1 高原空气热力学参数Table 1 Thermodynamic parameters of plateau air

2 散热器传热计算方法

工程车辆上常配备的散热器有管带式散热器和板翅式散热器，以某型装甲车辆的高温循环管带式散热器为研究对象，空气侧采用波纹型翅片，芯体结构和散热器实物如图1所示。

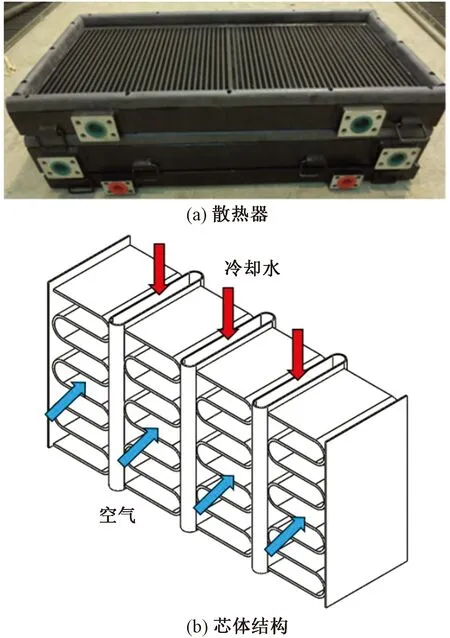
图1 散热器及芯体示意图Fig.1 Radiator and sketch of radiator core

散热器换热量利用热平衡方程式表示为

Q=h0AΔt

(3)

式(3)中：Q为传热量；h0为平均换热系数；A为传热表面积；Δt为对数平均温差。

散热器传热量同时可以通过冷热流体质量流量和温度变化进行计算[7]，表示为

Q=mccp,c(t″c-t′c)

(4)

Q=mhcp,h(t′h-t″h)

(5)

式中：m为流体质量流量；cp为流体的比热容；t′为流体进口温度;t″为流体出口温度；下标c和h分别代表冷流体空气和热流体冷却水。

在散热器工作过程中，热量首先通过冷却水与管壁之间进行对流传热，再由管壁向翅片进行导热，最终由空气与翅片之间的对流传热带走热量，将式(5)代入式(3)，可得

(6)

式(6)中：hc为冷却空气与翅片之间的对流传热系数；hh为冷却水与管壁之间的对流传热系数；k为散热器的导热系数；δ为水管厚度；Ac为空气侧翅片的传热面积；Ah为冷却水侧传热面积；η为翅片的肋效率。

在这三种传热过程当中，只有空气与翅片的对流传热会受海拔高度变化影响，将式(6)后两项当作常数C1来处理，即

(7)

翅片的传热面积和肋效率都为其物理特性，同样不受海拔高度变化影响[8]。因此，主要针对翅片与空气对流传热系数hc进行研究，即

(8)

式(8)中：Re为雷诺数；Pr为普朗特数；j为传热因子；de为当量直径。

波纹形翅片传热因子j通过经验公式[9]表示为

在挖掘堤坝地基时首先应严格按照设计要求对地基进行勘测，做好路线划定工作；其次，采用机械式开挖，以取代传统人工开挖，这样一来，开挖深度可以达到工程要求，同时还能充分保证施工质量、降低施工难度，确保按期完成工程进度；第三，开挖之后的地基应进行碾压处理，避免建设好的工程出现坍塌问题，造成裂缝渗水问题的出现，确保水利工程的安全性。

(9)

式(9)中：Fp为散热带节距；FH为散热带高度；2H为波高；LD为散热带宽度；L为波距。

雷诺数Re表示为

(10)

式(10)中：ρ为空气密度；v为空气流速；μ为动力黏度。

3 散热器单元CFD仿真

为确定多孔介质的孔隙率、黏性阻力系数和惯性阻力系数，利用Fluent对散热器单元在平原环境下的不同工况进行仿真。

空气侧和水侧入口设置为速度入口，出口设置为压力出口，冷却水入口温度设置为370 K，空气入口温度为300 K，在风速为5 m/s下散热器单元翅片的温度变化如图2所示，压力变化如图3所示。

为计算多孔介质的黏性阻力系数和惯性阻力系数，对不同风速下的散热器单元仿真得到空气进出口压力差，仿真结果如表2所示。

图2 风速5 m/s下散热器单元翅片温度Fig.2 Fin temperature of radiator unit at 5 m/s air speed

图3 风速5 m/s下散热器单元翅片压力Fig.3 Fin pressure of radiator unit at 5 m/s air speed

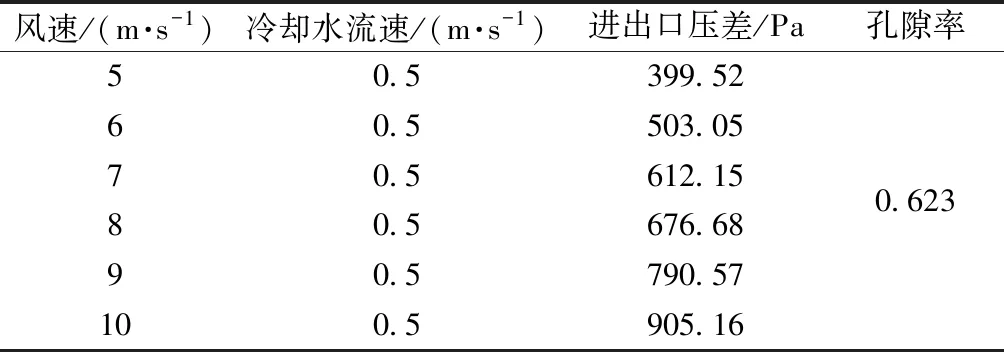
表2 散热器单元仿真结果Table 2 Simulation results of radiator unit

将仿真结果中的进出口压力差值和气侧风速进行二次多项式拟合，拟合公式为

(11)

式(11)中：Δp为气侧进出口压力差；v为气侧风速；a、b为待拟合参数。

多孔介质的模拟方程是通过在标准流体流动方程中加入动量源项来构建的，动量源项由两部分组成，一部分是黏性损失项，另一部分是惯性损失项。其表达式为

(12)

式(12)中：Si为坐标轴i方向上动量方程中的源项；α-1为黏性阻力系数；μ为动力黏度；vi为坐标轴i方向上的速度；C2为惯性阻力系数；ρ为流体密度。

关联压力降与动量源项方程为

Δp=-SiΔn

(13)

式(13)中：Δn为多孔介质区域厚度。

联合式(11)～式(13)得

(14)

(15)

代入数值计算得到黏性阻力系数α-1=1.964×107，惯性阻力系数C2=25.212。

4 散热器整体CFD仿真

管带式散热器为单流程结构，尺寸为973 mm×731 mm×178 mm，具有420个冷却水通道，整体主要由进水口、水室总成、芯体、出水口构成，利用Solidworks建立几何模型，模型如图4所示。冷却水由进水口流入，通过水室总成流至散热器芯体，经气侧带走热量后，由出水口流出。

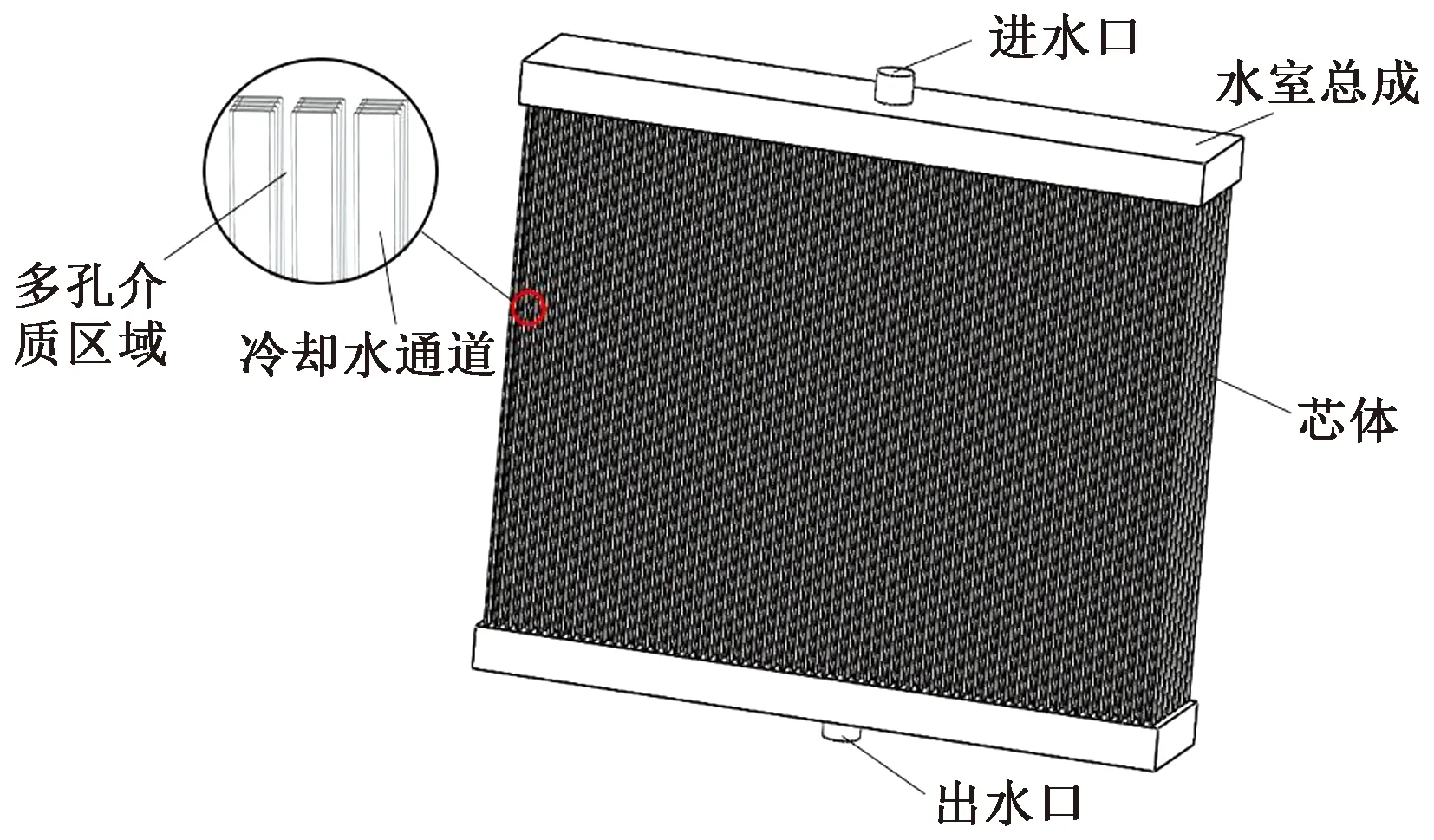
图4 散热器几何模型Fig.4 Radiator geometry model

图5 散热器整体网络Fig.5 Mesh of whole radiator

使用有限元前处理软件Mesh对散热器整体进行非结构性网格划分，在温度、流速等梯度值较大的区域，进行网格加密来保证计算精度，划分后的散热器模型如图5所示，总单元数为320万，节点数为106万。

空气侧入口边界设置为速度入口，出口边界设置为压力出口，水侧入口边界设置为流量入口，出口边界设置为压力出口。

海拔高度为0 m，气侧温度为308 K，水侧入口流量为120 L/min，温度为377 K，对不同进口风速下散热器散热情况进行仿真，其中温度场仿真结果如图6所示。

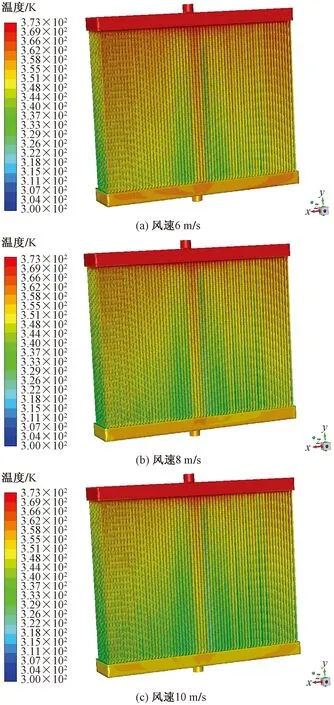
图6 散热器温度场Fig.6 Radiator temperature field

由温度仿真云图比较可知，随着风速的增加，散热器表面温度降低。当风速由6 m/s上升到10 m/s，散热器出水温度由356.7 K下降到353.4 K。散热器芯体两侧的冷却水通道相比中间通道温度下降较慢，是因为冷却水从进水口进入，在水室总成内分流入各通道，位于两侧的通道冷却水压力较低，水流速度相对较慢，产生了芯体两侧比中间温度高的仿真结果。

为验证模型准确性，在风洞实验室针对上述工况点开展了散热器单体风洞试验，实验结果与仿真结果对比如图7所示。

图7 散热器散热量试验值与仿真值对比Fig.7 Comparison between experimental value and simulation value of radiator heat dissipation

从试验结果可知，实验结果符合预期的仿真趋势，随着风速的升高，散热器的整体散热量随之上升。图7绘制了5%的误差棒，比较实验值与仿真值可知，散热量的仿真值落在试验值的误差棒范围内，可以认为该散热器计算模型较为准确。误差的原因是由于传感器精度误差和环境因素的影响造成。

5 散热器变海拔性能分析

5.1 海拔高度对散热器传热性能的影响

图8、图9为气侧温度为308 K、冷却水流量120 L/min、进水口温度为373 K的条件下，不同海拔高度和不同风速对散热器表面换热系数和散热量的影响。

随着海拔高度的升高，空气密度逐渐降低，由雷诺数计算公式[式(10)]可知，风速、空气密度与雷诺数呈正比关系，因此，随风速和空气密度的减少，雷诺数也相应降低，流体流动状态发生改变。由于雷诺数与换热系数呈正比关系，导致散热器换热系数随雷诺数的减小逐渐降低，使得散热器在高原散热能力显著下降[10]。当海拔高度由0 m升高到5 000 m时，散热量由166.5 kW下降到111.8 kW，下降幅度为32.9%，换热系数由212.95 W/(m2·K)下降到162.73 W/(m2·K)，下降幅度为23.6%，海拔每升高1 000 m，换热系数下降约4.72%，散热量下降约6.58%。

图8 散热器散热量随海拔高度变化规律Fig.8 The law of radiator heat dissipation varying with altitude

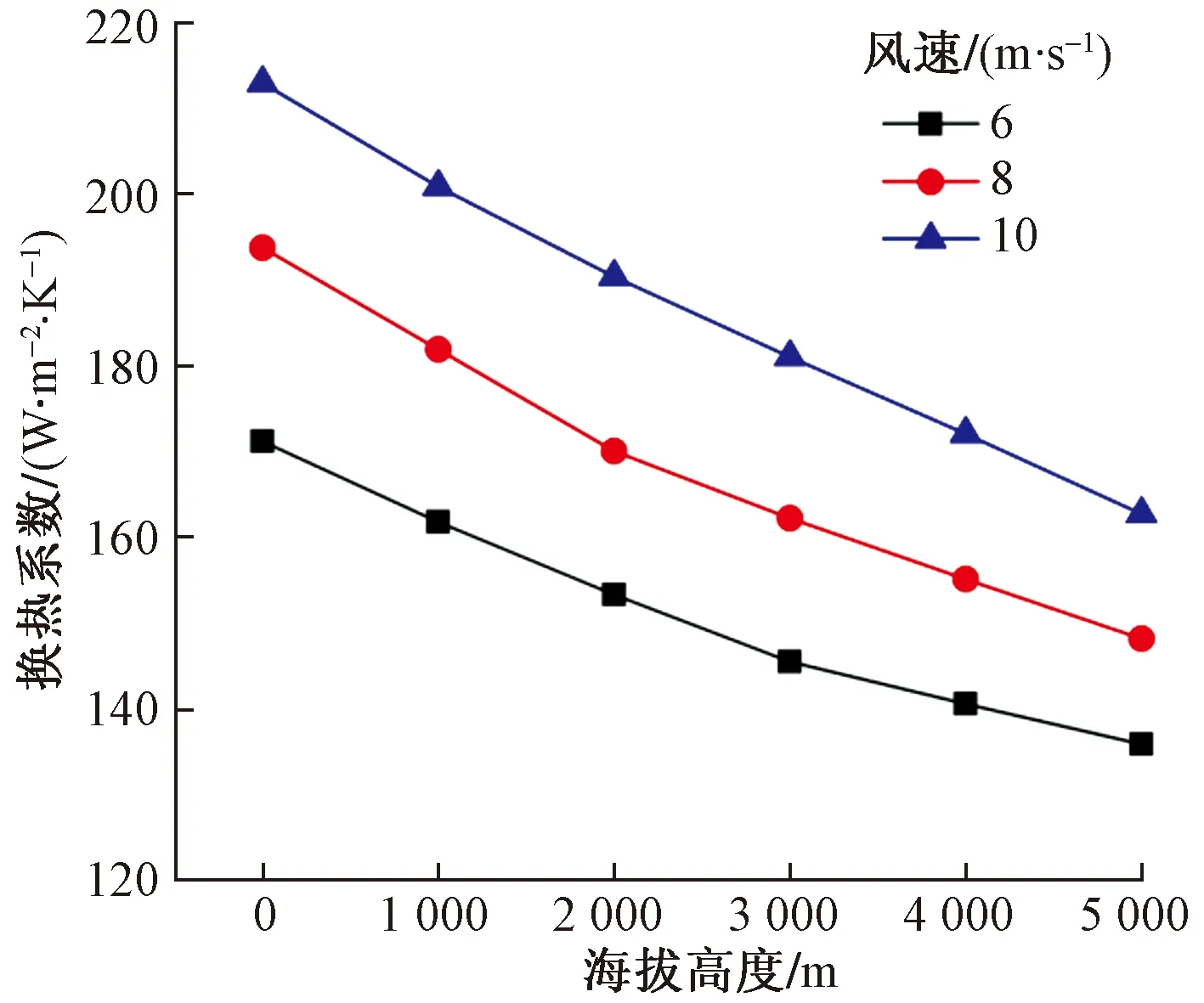
图9 散热器换热系数随海拔高度变化规律Fig.9 The law of radiator heat transfer coefficients varying with altitude

5.2 环境温度对散热器传热性能的影响

图10、图11为不同环境温度下，海拔为0 m和4 500 m时散热器的散热量与换热系数变化趋势。环境温度对散热能力的影响主要表现在环境温度越高，其与冷却液的温度差越小，导致二者之间的换热系数降低，相同流速的冷却空气条件下，散热能力减弱[11]。

计算过程中，流经散热器芯体的冷却空气流速为10 m/s，冷却水流量为120 L/min，冷却水温度为373 K。在平原环境下，当环境温度由273 K上升到323 K时，散热器散热量由203.09 kW下降到109.54 kW，下降幅度为46.1%，换热系数由217.56 W/(m2·K)降低到207.12 W/(m2·K)，下降幅度为4.8%，这是因为环境温度的升高导致气侧与水侧的温差降低，同时空气随着温度的升高，气体密度减小，雷诺数降低，导致换热系数略有下降，二者共同作用直接影响散热器散热量。当海拔高度升高到4 500 m时，气压的降低同温度一样会导致空气密度的下降，影响气体雷诺数，使得散热器换热系数和散热量与平原相比呈现降低趋势。

图10 散热器散热量随温度变化规律Fig.10 The law of radiator heat dissipation varying with temperature

图11 散热器换热系数随温度变化规律Fig.11 The law of radiator heat transfer coefficients varying with temperature

6 结论

(1)对于散热器结构复杂、翅片部分尺寸过小、CFD仿真不易划分网格的问题，采用多孔介质模型替代散热器翅片部分，可在保证一定仿真精度的同时极大减少模型计算量。

(2)散热器的散热量和换热系数受环境因素影响较大，气压降低和环境温度升高都将导致散热量和换热系数的降低，究其原因是因为二者都将导致气体密度的降低，影响气侧雷诺数的变化。海拔每升高1 000 m，散热器散热量和换热系数分别下降6.58%和4.72%。

(3)在对车用散热器进行设计和优化匹配时，必须考虑其在高原环境下的性能变化规律，进而对散热器的传热模型参数进行必要修正，才能使得计算结果更贴近实际情况。