基于系统动力学的高铁客运需求预测

牟振华，李克鹏，陈艳艳，闫康礼，李 想，申栋夫

(1.山东建筑大学交通工程学院，济南 250101；2.北京工业大学城市交通学院，北京 100022)

改革开放四十多年来，中国的长距离客运事业取得了长足的进步，人们长距离出行的质量也逐步提高。截止到2019年底，中国的高铁运营里程已经超过3.5万km[1]，高居世界第一，成为中国交通强国战略的重要组成部分。高铁作为新兴的运输工具，以运速快运量大的优点吸引了大量的中长途客流[2]，也引起了中国长途客运结构的变革，以公路运输为主的局面逐渐向以轨道运输为主转变。按照中国的中长期铁路网规划，高铁是传统普通铁路的升级替代品，高速铁路的建设方兴未艾。高铁的运输需求预测是高铁规划和建设的重要基础，预测结果的准确性和可行性对中国高铁产业的发展有着巨大的影响。

交通需求预测是一个具有较长历史的研究方向，也是交通运输学科的一个重要研究分支，在学科发展过程中，产生了如时间序列[3]、灰色模型[4-8]、模糊预测[9]、神经网络[10-12]、重力模型[13]等一批被广泛应用且取得较好成果的研究方法。随着相关学科的发展，也由于基础数据的获取来源变得多样化，也逐渐产生了一些新的方法，例如适用于多维度大数据的支持向量机(support vector machine,SVM)模型[14]，适合周期性波动的需求预测的整合移动平均自回归模型(Autoregressive Integrated Moving Average model,ARIMA)[15-16]，另外还有多种模型的组合使用，如奇异谱分析模型[17]，Markov链+灰度模型[18]等，以上这些模型方法都在各自适合的领域的需求预测方面发挥了重要的作用。然而，高铁运输系统是个复杂的巨系统，受到政策、经济、人口、环境等内部和外部因素的广泛影响，同时高铁也在很大程度上影响着沿线城市的经济发展[19-21]，以上模型从某个单一层面对其需求进行预测分析都显得不够全面，且无法对变量的敏感性进行分析。系统动力学(system dynamic，SD)模型则可以有效地规避以上缺点，从系统、全面的角度分析各种相关因素对高铁客运需求的影响，还可以考虑历史周期数据的变动因素对预测的影响，能够设定不同要素组合的多模式情景对高铁需求进行预测和变量的敏感性分析[22]，是进行复杂系统需求预测的适用方法。系统动力学模型已经在污染物排放[23-24]、能源电力和工业产品[25]需求预测等方面有了较多应用，在交通运输方面已经有了其在铁路运输需求[26]、航空客运需求[27-29]、城市公交及投资需求[24,30-31]、城市低碳出行需求[23]等方面的研究成果。现拟在已有研究的基础上，区分高铁与铺贴客运需求差异，深入分析高铁运输需求与居民收入水平、人口数量、行业投资的相关关系，建立相应的系统动力学预测模型，并预测多情景下的高铁需求变化。

1 模型原理与影响因子分析

系统动力学是由Jay W.Forrester教授创立并用于企业管理优化的系统仿真方法，经过几十年的发展与演化，已经成为系统科学与管理科学的重要分支和研究工具。系统动力学认为系统组成部分之间存在着信息的传递和回馈，强调从系统高度认识各个组成部分之间的关系，反对割裂成独立系统，适合处理高阶、多回路和非线性的反馈结构[22]。系统动力学的工作流程一般分为4个主要阶段，如图1所示。

图1 系统动力学的工作流程Fig.1 Workflow of system dynamics

高铁客运需求是社会经济发展过程中派生出的高等级出行需求，是国家经济和社会活动发展的晴雨表，受到经济、社会等因素的影响较大，其中良好的经济活动造就了大量出行需求，同时出行需求又促进了经济发展，增进了进一步进行交通设施投资增加交通供给的可能性，提高二三产业国内生产总值(gross domestic product,GDP)比重，三者互为正反馈。社会因素方面，人口数量及居民的社会经济特征是主要影响因素，由于高铁运输的服务质量高于普通铁路与公路运输，单位运价也相对较高，因此高铁出行者的职业、收入、人均出行次数、出行距离等社会经济特征也影响着出行需求。同时高铁运输与其他交通运输方式形成竞争，研究发现，在中长距离(400～1 000 km)出行领域，高铁对航空运输形成巨大冲击，“袭夺”了民航的部分中短途客源，同时高铁作为普通铁路的升级产品，对铁路客源也形成一定的冲击。其他方面例如运力供给、行业投资等因素也对高铁的运输需求产生影响。以上为系统动力学的建模边界，接下来将对模型中的影响因子进行分析。

1.1 产业构成因素

国民经济中的二三产业是引发交通运输需求的重要来源，二三产业比重越大，相关产也越发达，带来的客货运交通需求就会越大，因此，二三产业值及比重与高铁运输需求有较强的相关性。通过十余年的二三产业GDP值与高铁客运量进行了相关性分析，发现两者相关系数达到0.94，有较强的关联性,如图2(a)所示。因此将二三产业比重因素作为系统建模变量。

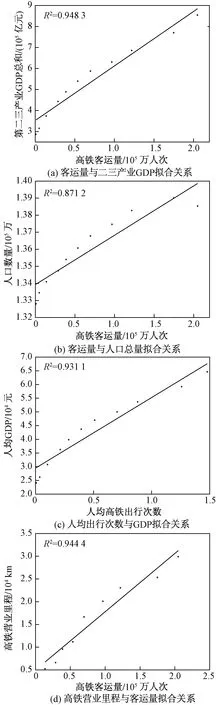
图2 主要因素间的相关性Fig.2 The correlation between the major factors

1.2 人口因素

人口是进行经济和社会活动的第一主体，随着经济发展，越来越多的人开始有了长距离出行需求，人口越多，对应的主体的客运需求就会越大，因此人口因素是需求预测研究中不可或缺的主体，通过分析人口与高铁客运量数据关系，发现两者相关性较高，如图2(b)所示,因此将人口总量因素作为系统变量。

1.3 人均GDP因素

人均GDP是个人消费能力的基础，一般而言，人均GDP与个人可支配收入成正比，人均GDP的提高必然带来生活水平的提高，居民的商务、旅游等出行次数也会有一定的增加，而且消费升级背景下，高铁、航空等作为快速、舒适的出行方式代表，会吸引更多的出行人群。分析了人均GDP与人均高铁出行次数之间的关系发现，两者的相关性较高，如图2(c)所示。人均GDP既与人口总量相关，也与GDP总量相关，因此将人均高铁出行次数也作为系统建模变量。

1.4 高铁建设因素

高铁的供给是高铁客运需求的重要供给侧因素，里程越长，覆盖率和通达水平越高，吸引更多的出行者采用高铁出行，目前中国高铁里程已经达到3.5万km，根据相关规划，高铁营业里程将继续增长。分析过去十年的运量与营业里程数据相关性发现，两者密切相关，如图2(d)所示。

1.5 其他方式竞争因素

从客运量数据上看，高铁的运量占比已达65%，且呈现逐年上升的趋势。从近几年的二者客运量和周转量来看，普通铁路的周转量和客运量都呈现下降趋势，高铁则大幅增加。因此研究认为普通铁路对高铁的竞争性影响极小，高铁“袭夺”了普通铁路的客源，高铁是普通铁路的升级替代产品。历史年度的高铁出行距离与出行次数如图3所示。

图3 历史年度的高铁出行距离与出行次数Fig.3 Historical annual travel distance and travel times of high-speed railway

其他方面，从高铁出行的距离因素来看，自2010年来的高铁单次平均出行距离稳定在340～400 km，呈现由低到高再降低的趋势，分析原因是高铁里程迅速增长，高铁可达性增强，带来人均出行距离增长。2014年以后，高铁里程和高铁运输周转量仍在逐步增加，但是总的高铁可达性大幅增加，旅客出行的直达性提高，又使得单程的平均出行距离又开始回归，为1～1.2 h的高铁车程，考虑到民航在长距离(1 000 km以上)运输方面的绝对优势，预测未来高铁的平均运距将继续保持在现有区间规模上，且未来民航对高铁持续形成竞争格局。虽然目前部分城市提出“空铁联运”的合作模式，但是联运运量仅占航空运量的2%，对高铁的影响微乎其微，因此暂不考虑民航的“合作”影响。

人均出行距离会随着收入增加而逐渐增加。从高铁和其他竞争出行方式的平均运距数据来看，民航方式由于运速优势其平均出行距离逐年上升。因此在高铁保持现有运送速度的模式下，由于收入增加而引发的出行距离增长的部分将会转移到民航方式，因此将民航作为高铁的竞争因素。

2 因果关系分析

高铁出行需求的系统动力学模型及其相关的因果关系图如图4所示，以测量不同影响因素对高铁需求因时间累积而产生的正(负)效应，图中箭头的正负号代表对变量之间的正负相关性。系统中各因素间的关系复杂，需要建立因果反馈环以定性表达系统中各要素之间的相关关系，是系统动力学建模的关键步骤。通过梳理因果关系图，可以观测到该模型的主要反馈环有如下几个。

环1：二三产业GDP→+人均二三产GDP→+人均出行次数→+出行需求→+高铁出行量→+行业利润→+二三产业GDP。

此环为正反馈。根据已有研究，国民经济的发展居民出行需求增加的决定性因素，出行需求增加又推动了运输行业发展，运输行业发展又会促进国民经济的增长，反映了出行需求与二三产业经济活动的互动关系。

环2：交通系统投资→+长距离出行设施供给→+运送速度→+服务水平→+运价→+行业利润→+交通系统投资。

这个环也是正反馈环。交通系统投资提高了运输系统的服务水平，进而可以诱增更多的出行需求，创造更多的行业利润反哺投资，是系统的正作用。

环3：高铁运输需求→+运力不足→+运价→-人均出行次数→+高铁运输需求。

这个反馈环为负。出行需求的增加会使高铁运输供给短缺，从而提高市场供给的价格，票价提高又会影响出行需求，这个反馈环反映了运力供给与出行需求之间的关系。

环4：交通设施投资→+二三产业GDP→+居民可支配收入→+出行距离→+长距离出行需求→+民航竞争→-高铁出行量→+行业利润→+行业利润→+交通设施投资。

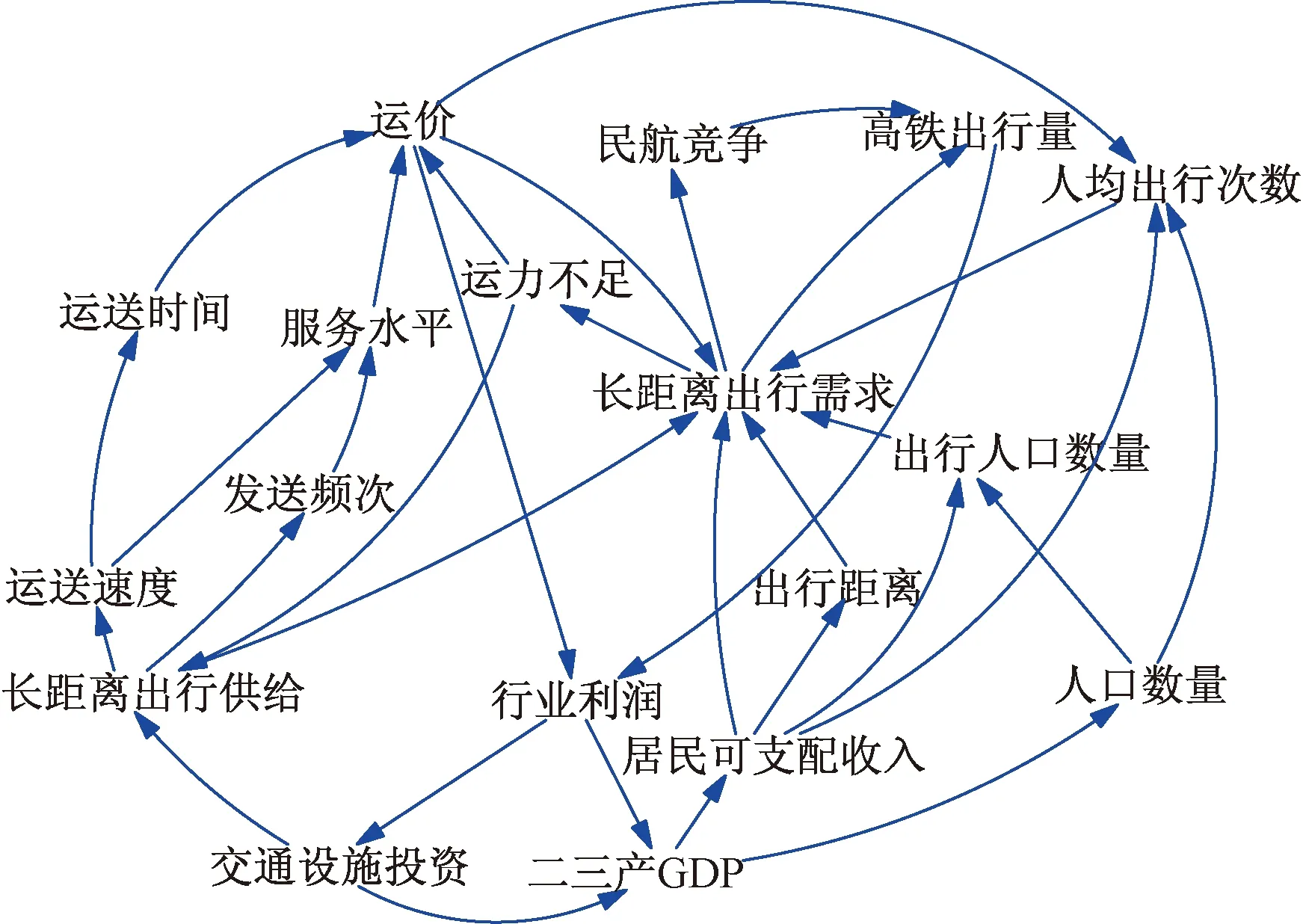
图4 因果关系图Fig.4 Causal loop diagrams

此环为负环。反映了交通设施供给与交通需求增加及民航对高铁需求的竞争关系。

3 模型建立与检验

通过因果循环图可以定性地表述系统内各变量间的逻辑关系，而系统流图(图5)则可以利用水平变量、速率变量和辅助变量定量地描述系统内各因素的相关关系，可以利用VENSIM软件进行构建。

人口、经济、设施、民航竞争等各个子模型的DYNAMO方程为

yr=zrgcr

(1)

sr(t)=sr(t-dt)+(rc-rs)dt

(2)

zr=sr-rs+rc

(3)

rc=srrcr/1 000

(4)

rs=srrsr/1 000

(5)

rcr=rcrlookup(T)

(6)

rsr=rsrlookup(T)

(7)

gcr=cg/sr

(8)

yj=zrGDPzrg

(9)

GDP(t)=GDP(t-dt)+zGDPdt

(10)

zGDP=GDPzGDPr/100

(11)

zGDPr=zGDPrlookup(T)

(12)

zrGDP=zGDP/sr

(13)

zrg=3.88×10-5zrGDP-1.144 4

(14)

ys=βzgy1

(15)

zgy2=zgy1lookup(T)

(16)

β=7.806

(17)

rgl=rgllookup(T)

(18)

ymj=mjlookup(T)

(19)

xgk(t)=xgk(t-dt)+xkzdt

(20)

xkz=yj+yr+ys-ymj

(21)

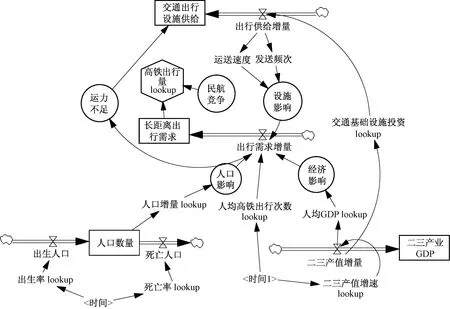
图5 系统流图Fig.5 System flow diagram

式中：yr为人口影响；zr为人口增量；gcr为人均高铁出行次数；sr为人口数量；rc为出生人口；rs为死亡人口；rcr为出生率；rsr为死亡率；cg为高铁出行量；yj为经济影响；zrGDP为人均二三产GDP增量；zrg为人均高铁出行次数增量；GDP(t)为二三产GDP；zGDP为二三产GDP增量；zGDPr为二三产GDP增长率；ys为设施影响；β为诱增因子；zgy1为高铁运营里程增量；zgy2为高铁营业里程增量；rgl为平均高铁出行距离；ymj为民航竞争影响；mj为民航竞争；xgk为高铁客运需求；xkz为高铁客运需求增量；t为变量的时间态，如二三产GDP(t)表示在年份t的二三产业GDP数量；dt为仿真步长，在本模型中取步长值为1年；T是系统设定的时间函数，用于调取仿真周期内的仿真时间。lookup( )函数为系统设置的表函数，可以读取预先设置在系统中有映射关系的多维变量数据，如死亡率lookup(T)是对时间变量(T)进行查找的表死亡率函数。在本研究建立的SD模型中，设定以 2010 年作为仿真起始点，设定9年模拟时周期，模拟时间步长为1年。研究抓取了2010—2018年的实际历史数据进行模型精度验证，计算了高铁出行量与客运周转量的仿真结果与真实数据的绝对误差和相对误差。

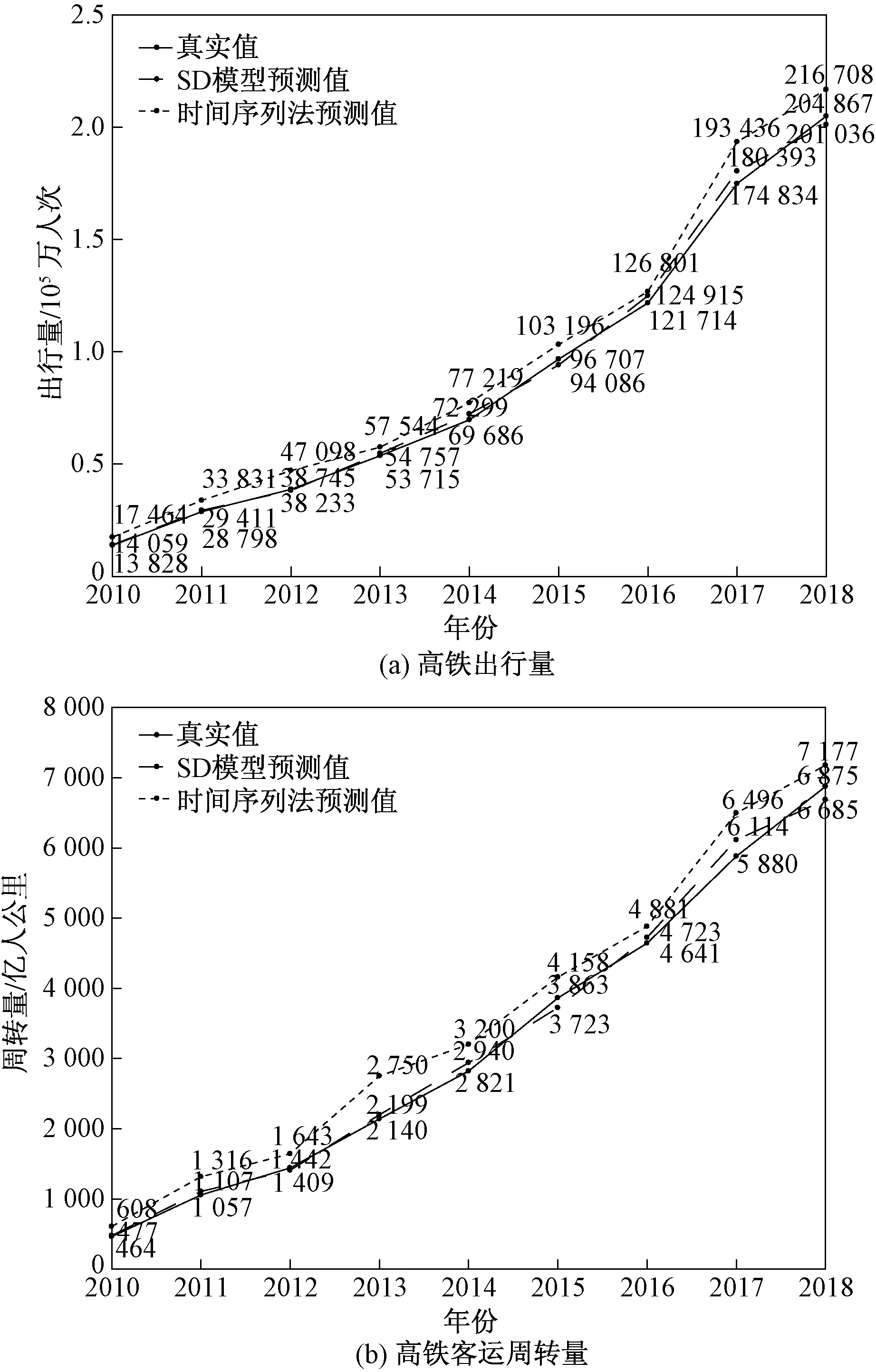
图6 模型误差分析Fig.6 Model error analysis

系统动力模型对模型的预测精度进行检验再进行仿真，一般以历史真实数据作为对照组。选取高铁出行量和周转量作为校核变量，依据国家统计年鉴、行业数据等数据源公布的数据对变量进行仿真拟合，与相对应的历史真实数据进行比较，校核显示两个检验指标的相对误差均在±5%之内，如图6所示，这个误差满足在95%信度水平下，检验指标误差±5%之内的系统动力学模型误差检验要求，且与传统的时间序列预测法相比较，显示精测精度有了较大幅度提高。满足精度要求的模型同时验证了其有效性，接下来利用该模型分析不同情境下对既定变量的影响。

4 多情景预测分析

4.1 情景参数值确定

根据中国现行的经济产业及人口政策，预判国家的发展趋势，确定系统动力学预测模型的相关参数值，依据公布数据可以进行经济、人口增长率以及人均出行次数的确定。

在经济增长率方面，中国的经济增长由高速增长逐渐进入中等稳定增长阶段，经济结构更加健康，经济发展更加具有可持续性，表现在数据上则是总体GDP增长率和二三产业GDP增长率增速的下降。从中国整体经济形势看，未来二三产业的增长将会继续拉动整体经济的发展，但考虑新型冠状病毒的近期和长期影响，其体现在增长率上的数字可能会被缩小，因此预计2020—2035年的二三产业GDP增长率为3%～6%。

在人口增长方面，《国家人口发展规划(2016—2030年)》指出，近年来中国人口生育率一直处于较低水平，因此国家微调了计划生育政策，可以使短期内的生育率提高，但是长期仍难以达到合理的更替水平。统计数据显示，近两年出生率相比全面二孩政策放开初期有所下降，为9‰～10‰。从长期来看，中国的生育观念正在发生较大变化，而医疗技术水平又在不断提高，因此人口总数量同时又会受人口老龄化等因素影响，预测出生率将稳定在较低水平上，同时死亡率持续小幅下降，人口总量长期稳定在较低的增长水平上。基于历史统计数据，预计2020—2035年的出生率为10‰～15‰，死亡率为7‰～8‰，人口自然增长率为2‰～7‰。

在人均高铁出行次数和出行距离方面，随着中国交通基础设施的进一步完善，城际运送速度和服务水平越来越高，城际出行时耗降低将会大大刺激中国的长距离出行需求。根据目前铁路部门发布的统计公报，截止到2019年，中国高铁人均出行次数约为1.64次,近五年年均增长率约为27.2%。基于目前中国的人均高铁出行次数水平和增长趋势，预计2020—2035年的人均高铁出行次数为1.8～3.0次。中国高铁运速目前已经相对领先，一段时期内将保持在这一优势水平上，因此预计高铁的单次平均出行距离将继续维持在1～1.2 h运距上，在此取350～400 km。

以上三个因素看似相互独立，但其实也有内在的关联性，已有研究表明，经济因素是影响人口因素和出行次数因素的主要变量[27]，经济繁荣则带来更多的人口生育和出行，反之则反之。因此未来情景模式主要依据经济因素的变化进行设定，根据经济增长情况设定为高增速、中增速和低增速三种状态，人口与出行水平依据经济增速进行参数确定如表1所示。

表1 情景参数设定Table 1 Scenario parameter setting

4.2 多情景预测

图7 2020—2035年高铁出行需求的多情景需求预测Fig.7 Forecast of multi scenario demand in 2020—2035

在设定的三种情景模式下，利用SD系统对2020—2035年的高铁运输需求进行进一步预测，得到三种模式下的高铁运量和高铁的运输周转量如图7所示。预测结果显示，未来中国高铁客运需求总量将保持先急后缓的上涨趋势，最晚于 2026年左右达到30亿人次，到2030年达到34亿人次，2035年达到37亿人次；从周转量来看，增长趋势与出行量基本一致，但是在高增长模式下增速明显加快，预测最晚于2024年达到1万亿人公里，2035年达到1.3万亿人公里。

5 结论与建议

从高铁客运需求产生的内在与外在系统机理出发，分析了与高铁出行需求相关的人口、经济、设施水平、民航竞争等因素的因果关系及定性及定量影响，构建了基于系统动力学的预测模型。验证了SD模型在高铁客运需求预测中的适用性和有效性，模型对高铁出行需求的预测相对误差在±5%以内，表现出了比时间序列法预测结果更高的精度。并根据人口、经济等要素设定不同的未来发展情景与参数，确定未来居民的人均高铁出行次数持续增长，人均高铁出行距离保持稳定的趋势，预测出中国未来不同情境发展下的高铁客运需求将持续上升，高铁客运周转量2035年达到1.3万亿km，高铁出行量2035年突破37亿人次，整体保持持续增长，但后期增速放缓。

基于以上结论，建议中国的高铁规划建设在2025年以后适度放缓增速，与需求增速放缓的趋势相适应。从民航竞争与合作的角度来看，高铁需要建立与时空需求相匹配的票价动态调整机制，同时不断提升服务质量，在中长距离出行服务市场与民航形成相互促进的良性竞争格局。