不同模量石墨简支梁的弹塑性分析及试验研究
赵建华, 顾文胤, 姚文娟*
(1.江西省高速公路投资集团有限责任公司上饶管理中心, 上饶 330025; 2.上海大学力学与工程科学学院, 上海 200444)
大量研究表明[1-2],许多材料都具有拉压不同模量性质。工程上广泛应用的材料,如土木工程中的混凝土,航空及机械工程中的金属、石墨、塑料等,都具有明显的拉压不同模量特性。21世纪初,人们发现强度最大的石墨烯材料是一种拉压不同模量的材料[1]。随着科学技术的发展,对准确描述材料的各种性能提出了更高的要求,研究材料的不同模量力学特性正在成为一种新的研究趋向。石墨广泛应用于各种工业领域中,比如电弧炼钢用电极、机械密封石墨环等。同时由于石墨材料具有良好的高温力学性能,再加上它本身的耐辐照性能,其在国防核工业中得到广泛的应用[2-4]。
21世纪以来,中外许多学者对不同模量材料制备的结构及力学特性进行研究[5-8],Insausti[9]通过虚拟试验研究了纤维增强复合材料的拉压不同模量。Yao等[10]利用理论推导并结合数值模拟方法,研究了双模量温克勒基础梁在温度沿梁高非线性分布下的力学特性。Li[11]推导了双模量功能梯度弯曲梁的解析解,确定了最大弯曲应力发生的位置。乔赫廷等[12]推导了有限元求解模型中切线刚度矩阵的列式,建立了基于拉压不同模量问题的数值求解算法。杨洋等[13]推导了拉压不同模量材料的剪切弹性模量表达式, 建立了不同模量铁木辛柯梁及欧拉-伯努利梁的振动微分方程,计算了不同模量铁木辛柯简支梁的自由振动频率。潘勤学等[14]建立了拉压不同模量的沥青路面结构数值计算方法。
以往的报道对石墨不同模量性能的研究缺乏,鉴于此,现通过单轴拉压试验,得到石墨的拉压模量比。并通过纯弯梁试验,得到石墨梁随荷载增加中性轴的偏移规律以及外荷载-应变关系。同时,采用不同模量理论对简支梁进行弹塑性全过程分析,将不同模量理论的弹塑性分析方法与石墨材料简支梁弯曲试验的实验值进行比较,以证明此方法的正确性。
1 单轴拉压试验
试验选取MSL82型号的石墨材料,分别制成4组截面直径Φ=10 mm,长L=50 mm的圆柱形试件和4组截面直径Φ=10 mm,长L=200 mm圆柱形试件。分别采用CMT5306电子万能试验机和WDW-E100电子万能试验机对其进行单轴抗拉试验和单轴抗压试验,测试内容包括:极限抗拉强度、极限抗压强度、拉伸弹性模量、压缩弹性模量以及计算拉压弹性模量比E+/E-。试验结果数据如表1所示。
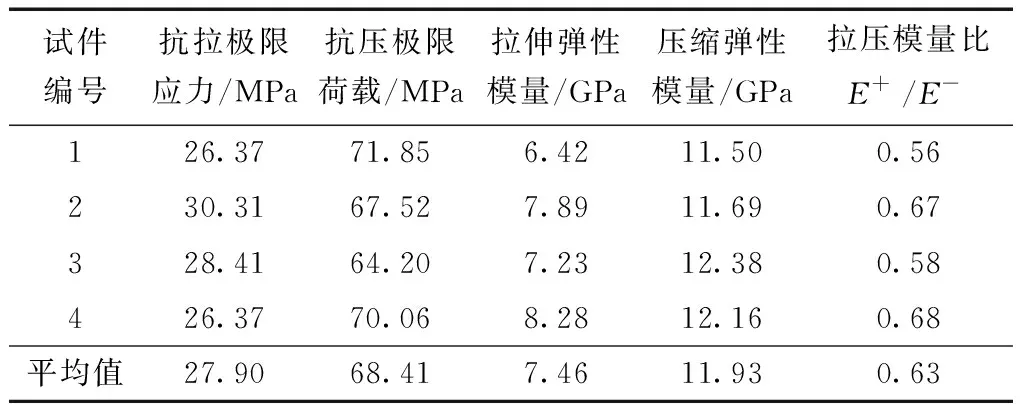
表1 MSL82型号石墨材料力学性能试验结果Table 1 Test results of mechanical properties of MSL82 graphite
通过对石墨材料的单轴拉压试验可知:石墨材料具有明显的不同模量特性,其拉压模量比E+/E-为0.63。
2 受弯梁试验及其结果
2.1 受弯梁试验
MSL82型号的石墨材料压杆稳定试验采用的是上海大学力学实验室的WDW-E100电子万能试验机(如图1所示),加载示意图如图2所示。

图1 试验装置与加载模式Fig.1 Test device and loading mode

F为外载荷
两个试件尺寸相同,均为矩形截面,杆件尺寸为长×宽×高=300 mm×45 mm×22 mm,如图3所示。每一试件中截面布置8片应变片如图4、图5所示。

图3 试件尺寸Fig.3 Specimen size

图4 MSL82型号石墨杆件Fig.4 MSL82 type graphite rod
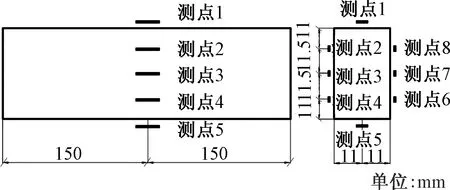
图5 应变片布置Fig.5 Strain gauge arrangement
2.2 试验结果
2.2.1 中性轴随荷载的变化
分别将测点2和测点8、测点3和测点7、测点4和测点6取平均值,然后利用测点1、测点5和上述三平均值拟合直线,通过几何关系(如图6所示),可求出随荷载增加时中性轴相对位置偏移量δ=Δ/h(如图7所示)。
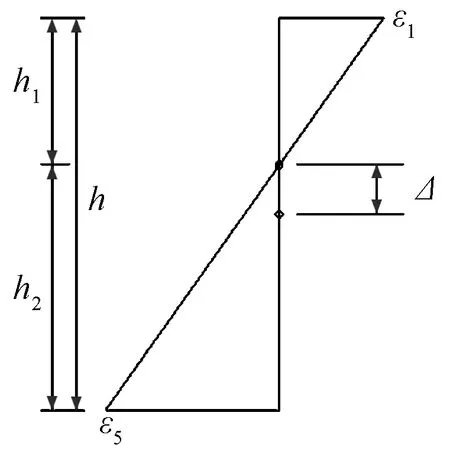
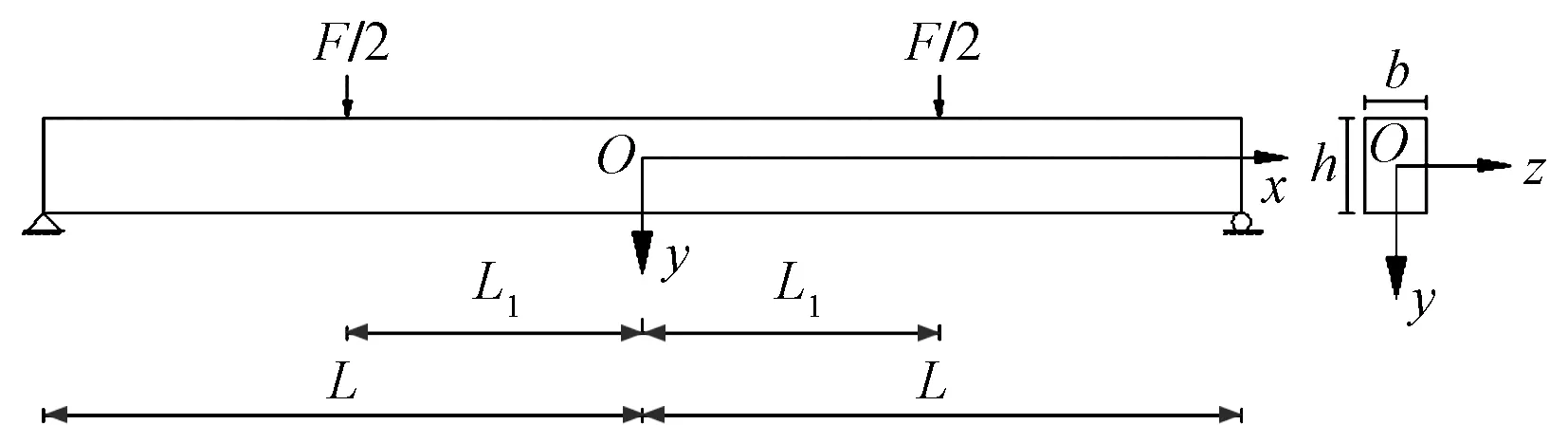
ε1为试件中截面上边缘处的应变量;ε5为试件中截面下边缘处的应变量;h1和h2分别为中性轴距上边缘和下边缘的距离;h为试件截面高度;Δ为中性轴变化后距截面中心的距离
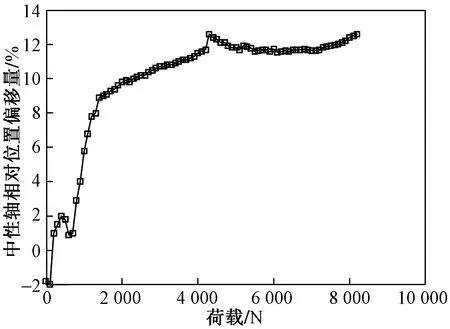
图7 中性轴相对位置偏移量Fig.7 Relative position deviation of neutral axis
由图7可知,梁的中性轴随外荷载变化的规律。在刚加载阶段,由于试验误差,中性轴的位置有点波动;当外荷载增加到了某一值时,中性轴的位置几乎维持在某一个水平;等到进入塑性阶段后,中性轴位置才会随着外荷载的增加而继续上升。
2.2.2 外载荷应变关系
将测点2与测点8取平均值作为新的测点2,将测点4与测点6取平均值作为新的测点4,然后分别绘出测点1~5的应力-应变(F-ε)关系曲线如图8所示。
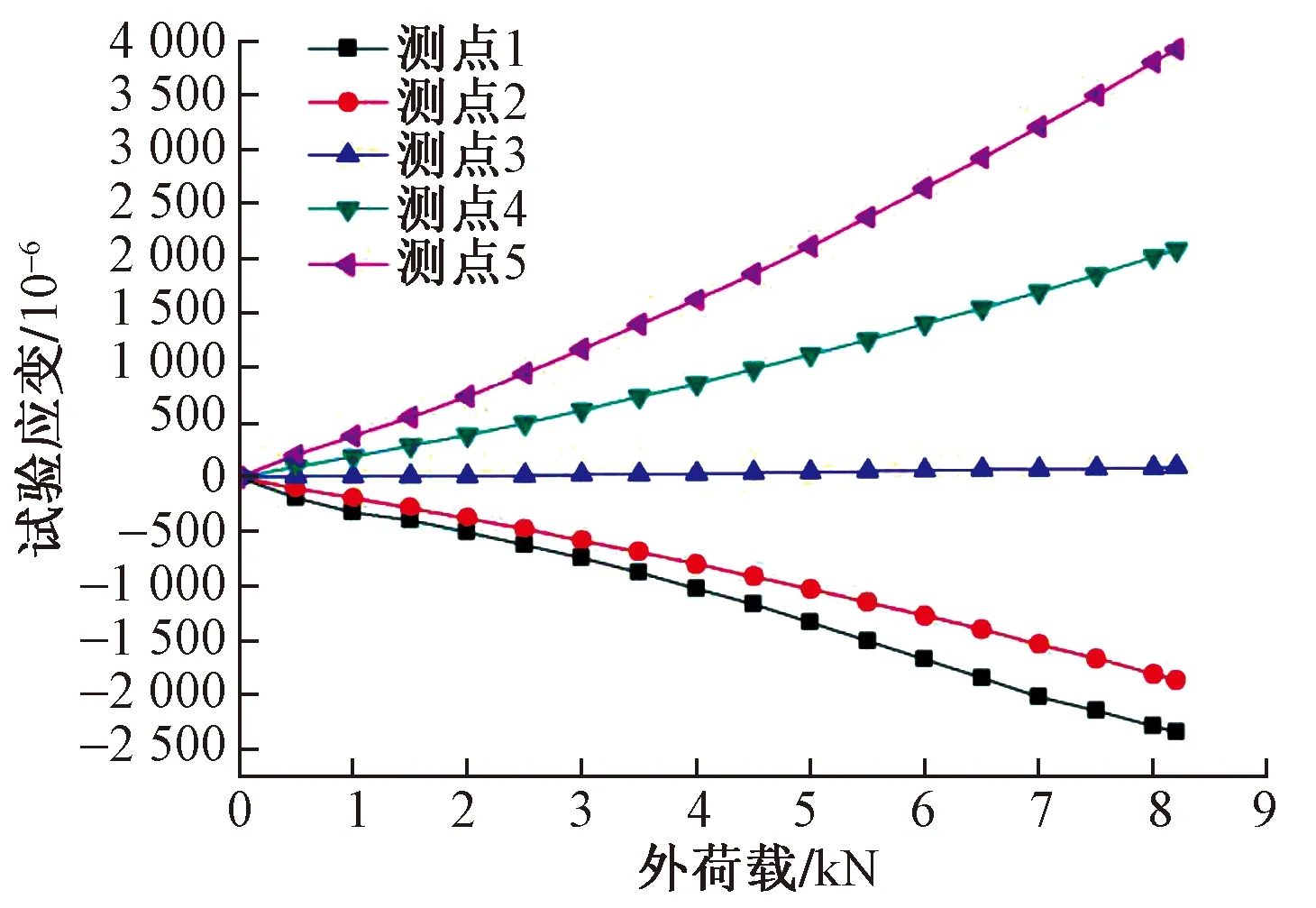
图8 应力应变关系曲线Fig.8 Stress-strain relationship curve
3 不同模量简支梁弹塑性过程分析
3.1 结构模型
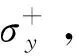
b梁为截面宽度;h为高度;2L为梁总长度;P=F/2为距梁端L1=L/2处作用的外荷载
3.2 应力应变公式推导
不同模量简支梁的弹塑性发展主要分为四个阶段:完全弹性阶段、弹塑性第一阶段、弹塑性第二阶段、完全塑性阶段。每一个阶段的应力应变的计算方法各不相同。
3.2.1 完全弹性阶段
对于完全弹性的矩形简支梁,前人已经做过研究,也有了相应应力应变解析式以及中性轴计算公式[8]。图10为弹性阶段截面的应力分布图。
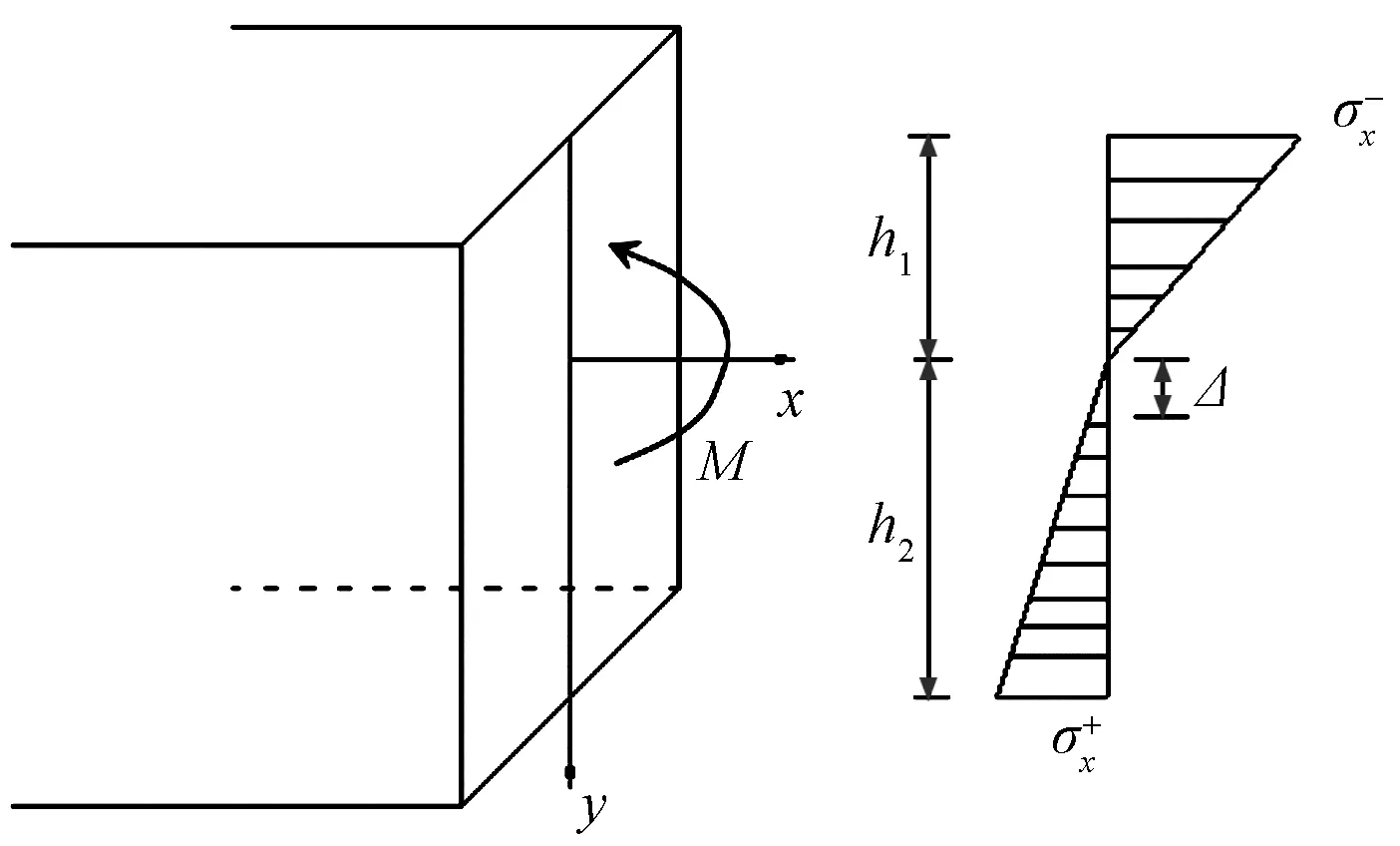
图10 截面应力分布图Fig.10 Section stress distribution diagram
引入拉压模量比a=E+/E-,应力应变公式变为
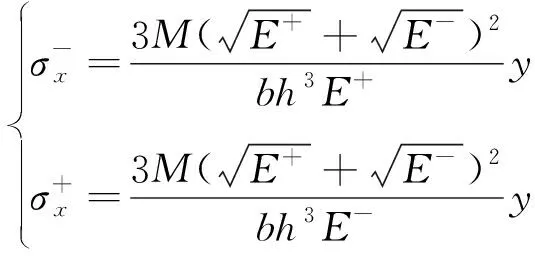
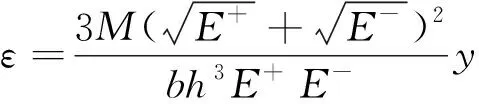
式中:M为截面处产生的弯矩;y为纵坐标值。
3.2.2 弹塑性第一阶段
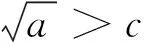
记梁中性层曲面的曲率为ρ,弹塑性第一阶段的截面应力分布图如图11所示。
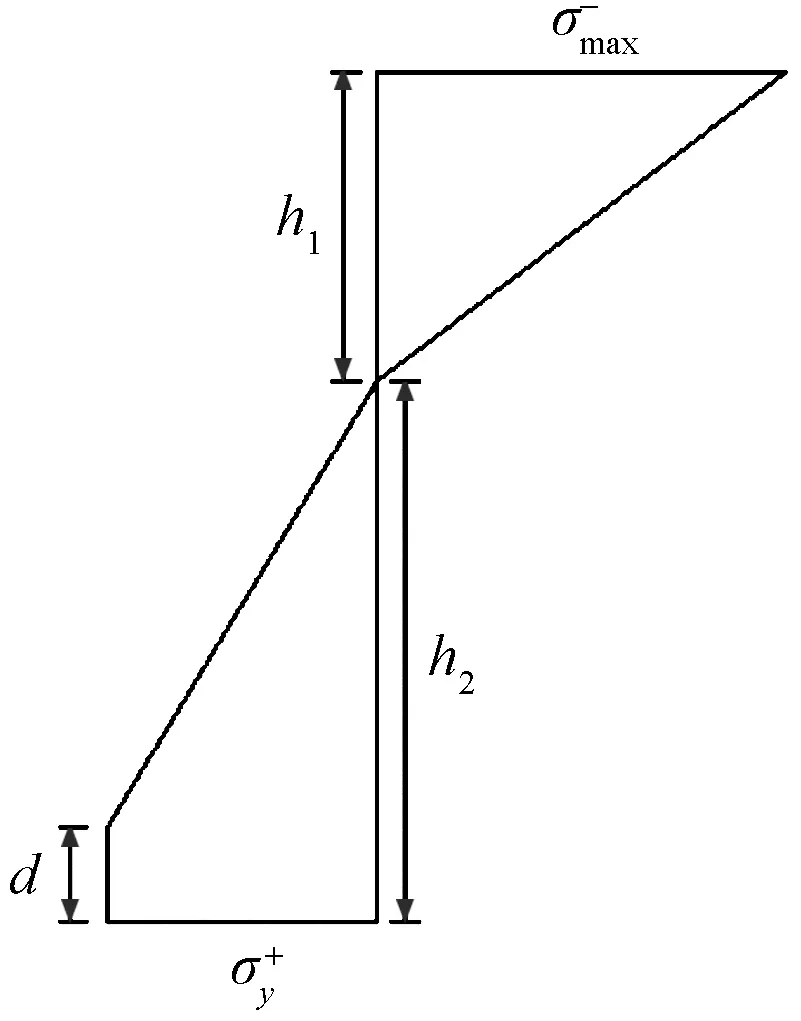
h1为梁的受压区高度;h2为受拉区高度;为受压侧弹性区的最大正应力;为受拉侧塑性区的最大正应力;d为受拉侧塑性区的截面高度
可以列出方程为
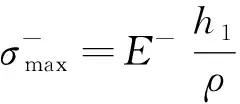

h1+h2=h(5)
根据平衡条件,可以得到水平方向力的平衡方程和弯矩平衡方程为
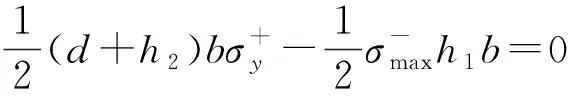

根据式(3)~式(7),可以整理得到式(8)、式(9)。
(1-a)h22-2hh2+h2+ad2=0 (8)
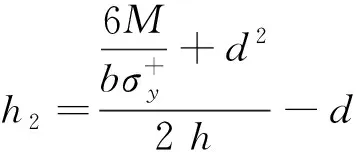
将式(9)代入式(8),得到关于d的一元四次方程式(10)为
h2+ad2=0 (10)
式(10)反映了外荷载F与塑性区高度d的非线性函数关系,左边可以用函数f(F,d)来表示。编制C程序,对于某个确定的外荷载F,以d值为自变量,d值的初始值为0.001 mm,步长为0.001 mm,终值为45.000 mm,对于每一个d值,验证是否满足关系f(F,d)-0.1<0,逐渐增大d值,直到满足关系式f(F,d)-0.1<0,跳出循环,从而求得对应于该外荷载F的d值。再根据式(9)求得受拉区高度h2,从而解得对应于该外荷载F的应力与应变。
受压区应力公式为

式(11)中:Mi为循环i次外荷载作用产生的弯矩值;di为第i次循环的d值。
受拉区应力公式为
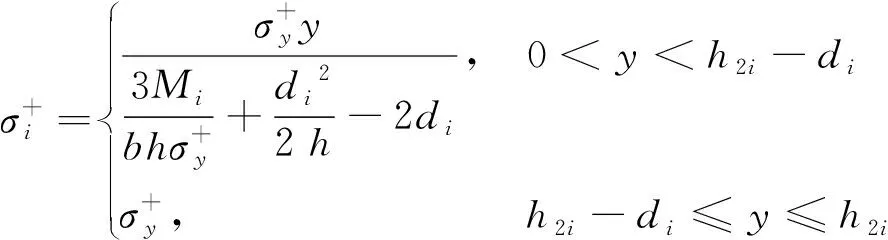
式(12)中:h2i为第i次循环的受拉区高度。
应变值为
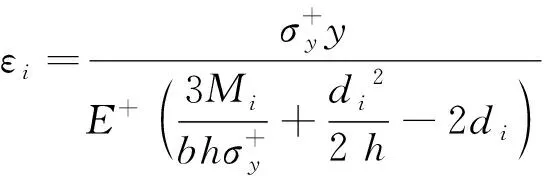
当i取值足够大时,应力和应变值都能连成光滑曲线,并用函数来拟合。
3.2.3 弹塑性第二阶段
当外荷载F增大到F2时,截面上部受压区边缘也发生屈服。图12为弹塑性第二阶段截面应力分布图。
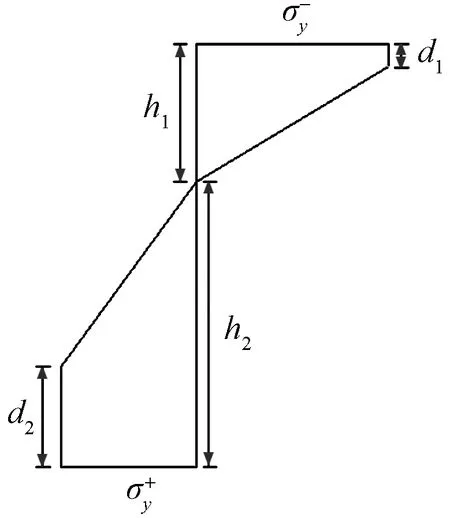
为受压侧塑性区的最大正应力;d1为塑性区高度;为受拉侧塑性区的最大正应力;d2为塑性区高度
根据图12,可以列出方程
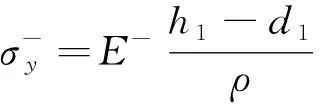
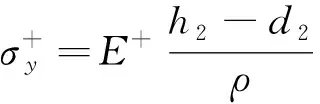
根据平衡条件,可以得到水平方向力的平衡方程和弯矩平衡方程为
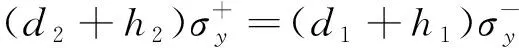
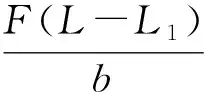
拉压模量比为a,拉压屈服极限比为c,根据式(5)、式(14)~式(16),可得
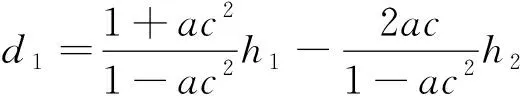
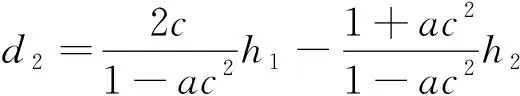
将式(18)、式(19)代入式(17)中,并联立式(5),得到关于h2的一元二次方程为
Ah22-Bhh2+λF-Ch2=0 (20)
式(20)中:A,B,C,λ均为常数,其表达式为
A=1+5c+(4+6a)c2+(6a+4a2)c3+
5a2c4+a2c5(21)
B=2c+8c2+12ac3+8a2c4+2a2c5(22)
C=3c-4c2-6ac3-a2c5(23)
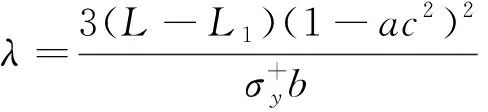
式(20)的解为
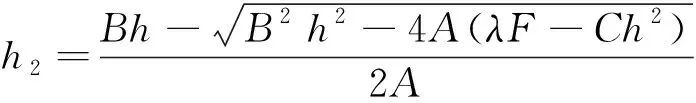
根据式(25),以及式(18)、式(19)可以得到h1、d1、d2的解,进一步得到应力应变公式。
受压区应力公式为
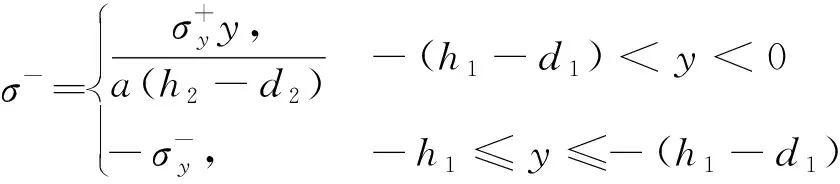
受拉区应力公式为
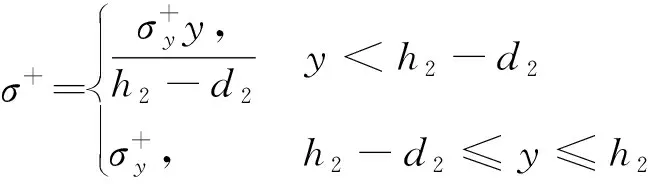
应变公式为
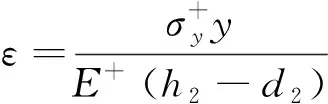
3.2.4 完全弹性阶段
假设材料为理想塑性的材料,那么,当荷载增加到某一值时,塑性可以达到饱满,从而形成塑性铰。塑性饱满时,d1=h1,d2=h2。图13为完全塑性阶段截面应力分布图。
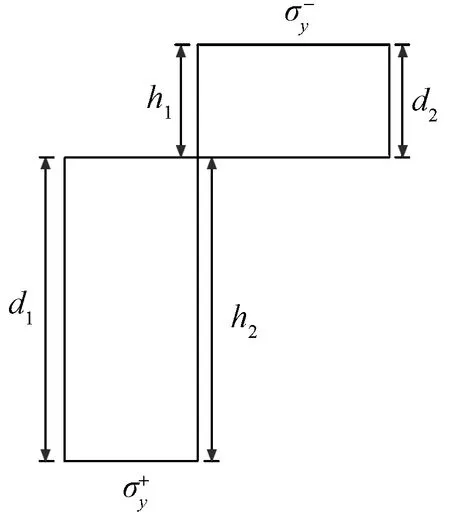
图13 完全塑性阶段应力分布图Fig.13 Stress distribution in complete plastic stage
此时的应力即为屈服应力

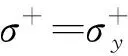
4 实例分析
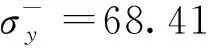
4.1 弹性阶段加载-应变关系的验证
不同模量弯曲梁的应变计算公式如式(2)所示,根据式(2)计算出各测点处应变的解析解,并与试验解进行对比,对比结果如图14所示。
从图14可以看出,不同模量弯曲梁的解析解计算结果与石墨受弯梁试验数据吻合,验证本文模型的正确性。
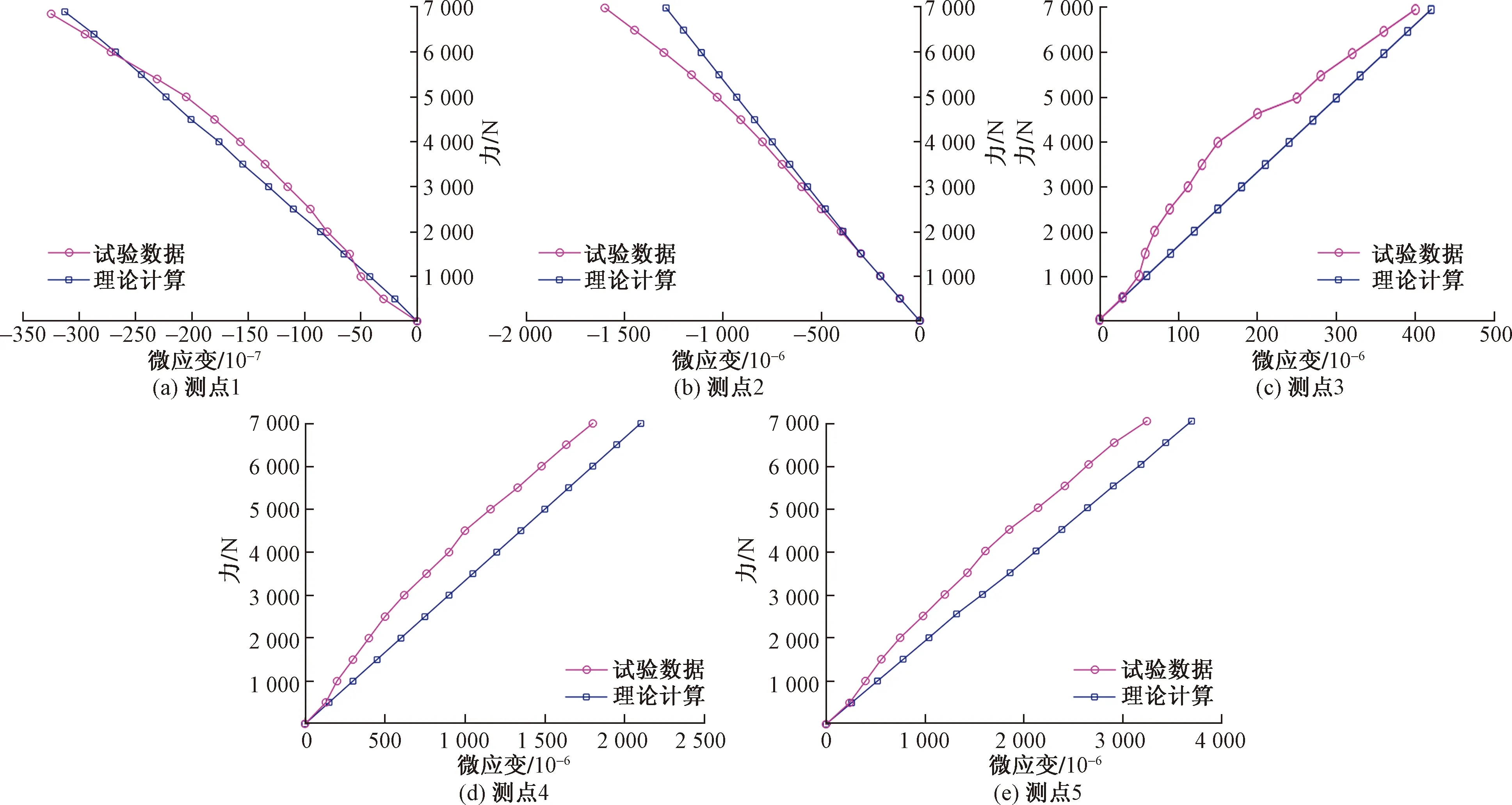
图14 弹性阶段的荷载-应变关系Fig.14 Load-strain relationship in elastic stage
4.2 弹塑性阶段加载-应变关系的验证
将试验中受弯梁的尺寸大小及受力特性等代入上述弹塑性分析方法的式(13)及式(28)式计算应变,理论计算结果与实验数据的对比如图15所示。
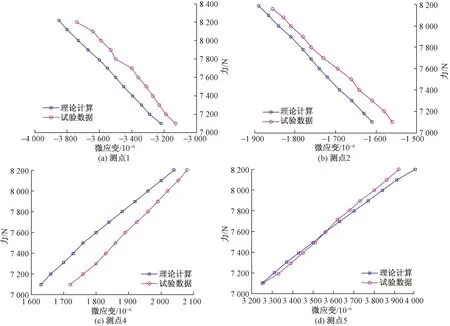
图15 弹塑性阶段的荷载-应变关系Fig.15 Load-strain relationship in elastoplastic stage
通过与石墨弯曲梁试验结果对比,可知所提出的弹塑性过程分析能够准确的描述不同模量简支梁受力进入弹塑性的全过程。由此,验证了本文模型的正确性。
5 结论
(1)石墨材料具有明显的不同模量特性,其拉压模量比E+/E-为0.63。
(2)通过与石墨纯弯梁试验结果对比,验证了建立的不同模量横力弯曲梁弹性解析解是准确有效的。
(3)从石墨材料受弯梁各测点的载荷-应变关系图可知,梁受拉侧应变明显大于受压侧,说明中性轴向受压(下)侧偏移。
(4)不同模量简支梁存在如下塑性力学特性规律。
①在弹性阶段,随外荷载增加,中性轴的位置保持不变;进入塑性阶段后,随着外荷载的增加,中性层的位置上升;中性轴最终的位置是由拉压屈服极限的比值决定的。
②在拉压屈服应力不变的情况下,随着拉压模量比的增大,弹塑性第一阶段的区间随之增大,而弹性阶段区间和弹塑性第二阶段区间都在减小。
③在弹性阶段,拉压模量比的大小对截面的应力分布有很大影响,减小拉压模量比,可以减小最大拉应力;而增大拉压模量比,则可以减小最大压应力;进入弹塑性阶段后,随着截面的塑性发展,拉压模量比对截面应力分布的影响越来越小。
④随着截面的塑性发展,拉压模量比对截面应变分布的影响比较大,因此,可通过改变拉压模量比来控制截面的最大拉压应变。当拉压模量比大于0.5时,进入弹塑性阶段后,拉压模量比越大,最大拉压应变均越大。

