考虑子系统恢复时间的停电电网分区策略

吴琛， 梁晟杰， 刘旭斐， 郁琛， 谢云云， 苏明昕， 苏波

(1. 云南电网有限责任公司电力调度控制中心,云南 昆明650011;2. 南京理工大学自动化学院,江苏 南京210094; 3. 南瑞集团(国网电力科学研究院)有限公司,江苏 南京211106;4. 智能电网保护和运行控制国家重点实验室,江苏 南京211106;5. 国网宁夏电力有限公司电力调度控制中心,宁夏自治区 银川750001)

0 引言

经济的增长和社会的发展使得现代社会愈加依赖电力行业的可靠运行。而即使电力系统规模愈加合理，结构愈加坚固，仍不可避免大规模停电事故的发生，且一旦发生就会造成巨大的经济损失和社会影响。如2003年的北美大停电，2006年的欧洲大停电及2009年的巴西电网大停电[1—4]都充分证明了这一点。因此，为了保证大停电后电力系统能够有序、快速恢复，减少社会损失，须预先制定电力系统恢复方案。

电力系统恢复主要分为3个阶段[5—8]：准备阶段[9]，系统恢复阶段[10]和负荷恢复阶段[11]。受系统运行复杂度影响，电力系统恢复所需时间较长。为了加快电力系统恢复进程，在电力系统恢复的准备阶段，通常根据电力系统中具有自启动能力的机组个数，将系统划分为多个子系统并行恢复，之后通过并网实现整个系统的恢复，提高电力系统恢复效率。

现有的黑启动分区研究中，一类研究主要基于电力系统网络拓扑特性，综合考虑黑启动电源约束、发电机-负荷平衡约束[12]、过电压和无功约束等，针对不同的目标函数如模块度[13]、负荷恢复量最大等，运用与图论[14]相关的方法进行求解，即GN算法[13]、谱聚类算法[11，15]、切割矩阵等[16]。而对于大规模电力系统，文献[17]运用基于有序二元决策图的决策方法降低了计算的复杂度。另一类则是提出了电力系统分区优化模型，文献[18]和文献[19]分别考虑了关键负荷的冷负荷特性、最小功率流对分区的影响。

上述研究均忽略了电网分区结果对电网恢复过程的影响，子系统大小不一的分区结果，导致恢复时间短的分区需要等待恢复时间长的分区恢复完成后再进行并网，系统总恢复时间长，黑启动效率低，停电时间长，社会损失大[20]。因此后续过程中系统的恢复用时对于黑启动分区策略具有显著影响，为了提高恢复效率，需要在分区过程中考虑分区结果对后续恢复的影响。

由此，文中在谱聚类分区的基础上，提出了基于粗糙集理论的分区修正算法。初步分区后，根据结果确定所有机组的决策属性和条件属性的取值，建立了带有不确定因子的决策表，筛选出待调整机组后，逐个调整机组，并不断更新决策表直至优化结束。该方法能够快速筛选待调整机组，一方面保证了分区的平衡，另一方面大大缩短了求解考虑恢复时间的电力系统分区优化模型的时间。

1 电力系统分区优化模型

文中介绍了现有基于谱聚类的分区方法和子系统恢复模型，分析了考虑子系统恢复的分区优化问题的难点，建立了考虑子系统分区恢复的优化模型。

1.1 基于谱聚类的黑启动子系统划分算法

根据电力系统的网络拓扑特性，将其抽象为有权无向连通图G，其邻接矩阵W定义为：当节点i和节点j相连时，则W中对应的元素为ωij，若节点i和节点j不相连，则对应元素ωij=0，因为G为无向图，所以ωij=ωji。其Laplacian矩阵L可以被定义为L=D-W，其中D为具有非零元素di的对角矩阵，W为图G的加权邻接矩阵，具有n个节点的图G的Laplacian矩阵L如下：

(1)

利用谱聚类算法的特性，将聚类问题转化为图的分割问题，使得子图内部相似度最大，子图相互之间的相似度最小。在Laplacian矩阵的基础上，将网络拓扑图映射到由其第二小特征值和第三小特征值所构造的二维空间内，再通过聚类方法k-means算法进行聚类，得到子系统划分结果。

对于某停电电网，划分其子系统的具体步骤如下：

(1) 根据电网的拓扑特性，将整个停电电网抽象成简单的网络拓扑图，停电系统的待恢复机组即为网络拓扑图的节点，线路即为网络拓扑图的边。

(2) 统计停电系统各个元件的信息，计算线路权值，构建对角矩阵D和度矩阵W，最后得到Laplacian矩阵。

(3) 根据谱聚类算法原理，计算Laplacian矩阵的特征值，并将其按从小到大排列，即λ1=0<λ2<λ3<…<λn。

(4) 取λ2和λ3分别作二维空间的横轴和纵轴，将网络拓扑图的节点映射到此二维空间内。

(5) 确定分区个数，运用k-means算法对聚类样本进行聚类，得到分区结果。

1.2 电网的分区优化模型

电力系统分区优化模型由目标函数和约束条件组成，具体如下：

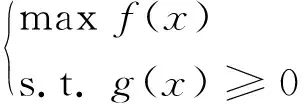
(2)

1.2.1 目标函数

大停电后电网恢复的根本目标是尽快恢复负荷供电，减少损失，所以用户希望停电时间越短越好。但因为最初分区结果只考虑网络的拓扑结构，所以容易造成分区大小不一，恢复时间相差悬殊，恢复时间短的分区需要等恢复时间长的分区恢复完成后才能进行并网，拖延了整个电网的恢复，所以以最小化电网恢复时间为目标，取子系统恢复时间中的最长恢复时间为整个电网所需恢复时间，其表达式为：

f=max{T1,T2,…,Tk}

(3)

式中：Tk为分区k的恢复时间。优化目标为通过调整分区内机组的位置，使得f尽可能小。

1.2.2 约束条件

对于大停电后系统来说，其约束条件主要包括等式约束和不等式约束。

(1) 机组启动功率约束。待恢复机组所需的启动功率应该小于分区内所有已启动机组在当前时刻所能提供的启动功率之和，待恢复机组i的启动功率约束定义为：

(4)

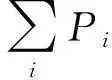
(2) 无功功率和自励磁约束。停电电网开始恢复时，会投入大量的空载高压线路向待恢复机组传送启动功率，因此线路上会产生大量的无功功率，如果其超出发电机的吸收能力，就会造成系统无功不平衡，所以线路上的无功功率要在发电机能够吸收的范围内，其表达式为：

(5)

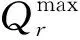
同理，大量的空载高压线路也会产生大量的容性无功功率，当容性无功负荷较大时，发电机定子电感与线路的容抗参数配合时会产生参数谐振，系统会产生自励磁问题。故线路上高抗补偿后剩余的充电功率要小于机组的额定容量与短路比之积，其表达式为：

(6)

式中：KCBi为机组i的短路比；SBi为机组i的额定容量。

为便于计算，可以将无功功率约束和自励磁约束合并为系统无功功率约束，其表达式为：

(7)

1.2.3 潮流和节点电压约束

潮流和节点电压约束为：

(8)

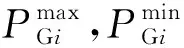
1.3 考虑子系统恢复时间的分区优化模型

由1.1节可以知道，谱聚类分区方法完全基于电力网络固有的网络拓扑特性进行分区，而电力网络的拓扑特性不会随着分区结果而变化。但1.2节中以子系统恢复时间最短为目标的电网优化模型，各个子系统恢复时间会随着不同的分区结果而变化，因此两者很难放在同一个模型中，故在基于谱聚类算法进行初步分区的基础上，再进行分区结果的优化。

文中建立了考虑子系统恢复时间的分区优化模型，不再仅以子系统恢复时间最短为目标，还考虑多个子系统恢复时间差距最小，即各个子系统大小更加均衡。分区优化模型的目标函数如下：

tij=|Ti-Tj|

(9)

f=min{tij}i≠j

(10)

式中：tij为各个分区之间的恢复时间差，i=1,2,…,n,j=1,2,…,n；目标函数f是子系统恢复最小的时间差，文中优化目标是使f尽量小。模型的约束条件与式(4)—式(8)一致。

2 基于粗糙集的分区优化模型的求解

由于子系统恢复是一个非常复杂的非线性优化过程，建立包含子系统恢复的分区优化模型较为困难。文中选择在基于网络特性进行分区的基础上，对分区结果进行修正。子系统修正为原始分区内发电机重新分类的问题，而粗糙集是现有研究中常采用的一种决策方法，已被广泛应用于故障判断[21—22]、图像处理[23]、大量信息处理[24—25]、智能控制系统[26]的研究中，如文献[21]就利用粗糙集的方法在黑启动分区前，对具有多个属性的网络进行信息处理。

2.1 基于粗糙集的带有不确定度的决策系统

粗糙集主要研究的问题之一是近似的集合，另一个是数据的分析和推理，所以基于粗糙集，有限的对象集合可以用有限的属性集合来表示[27]。在文中，考虑电力系统的表示方案，其中有限的待恢复机组集合可以用1组有限的属性集合来表示，即可以用信息系统S来表示整个电力系统：

S={U,R,V,μ,imp}R=C∪D

(11)

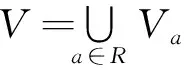
Vaij=ωi,j

(12)

(13)

文中将不需要调整位置的机组集合视为目标集合X，根据电力系统中的机组位置及属性，所有待恢复机组可以分到3个不相交的集合，即POS(X),BND(X),NEG(X)。若机组x∈POS(X)，则机组x一定属于目标集合X。若机组x∈BND(X)，则机组x一定不属于目标集合X。若机组x∈NEG(X)，则无法判断机组x是否属于目标集合X。

根据误差计算公式p(X)和n(Y)计算X划入POS,B(D)和NEG,B(D)的误差，其定义为[28]：

(14)

X划入正区的误差和Y划入负区的误差水平分别为δp和δN，即：

(15)

式中：δp，δN由电力系统初始分区结果决定。

2.2 考虑恢复时间的电力系统分区优化算法

电网分区优化模型的优化目标主要通过调整机组的所属分区来满足，为了使得分区大小均衡，将最大规模分区内的机组调整到最小规模分区中，从而均衡这2个分区的大小，缩短其恢复时间的差距，达到优化目标。算法具体步骤如下：

(1) 初始分区结束后，纪录每个待恢复机组所属的分区标签，分区标签大小即为该待恢复机组关于决策属性D的权值，最后组成VD集合。

(2) 根据分区情况，分别计算每个待恢复机组到k个分区黑启动机组的路径长度，路径长度即为该带恢复机组关于条件属性αk的权值，最后组成Vαk集合。

(3) 统计所有数据，确定μ和imp的值，组成带有不确定度的决策表。

(4) 根据决策表，计算各个待恢复机组划入POS,B(D)和NEG,B(D)的误差，并根据初始分区结果，确定要调整的机组个数，从而确定δp和δN的大小。

(5) 筛选出要调整的机组，并对这些机组进行调整。

(6) 每调整一个机组，计算各个分区的恢复时间，与上一次调整进行比较，如果时间有所缩短，就更新分区结果，并回到步骤(2)，重新构造决策表，调整下一个机组，直至待调整机组调整完毕。

3 算例分析

为了证明考虑恢复时间的电网分区优化算法的有效性，以IEEE 39和IEEE 118标准测试系统为例，说明文中优化算法的有效性，并与遗传算法求解的结果做比较。

3.1 IEEE 39标准测试系统

3.1.1 仿真场景

IEEE 39标准测试系统包含10台发电机机组，分别为30～39节点，其余29个均为母线节点，并含有12台变压器，34条线路。

假设黑启动初期电网全停，发电机30、32、37作为电力系统大停电后具有自启动能力的黑启动电源，其装机容量分别为250 MW，650 MW，540 MW。各机组的启动特性如表1所示，其中BS为黑启动机组，NBS为非黑启动机组，输电线路和变压器支路的启动时间均为5 min。

3.1.2 有效性分析

文中采用3种不同的方法对IEEE 39标准测试系统进行分区并进行对比，具体如图1和表2所示。

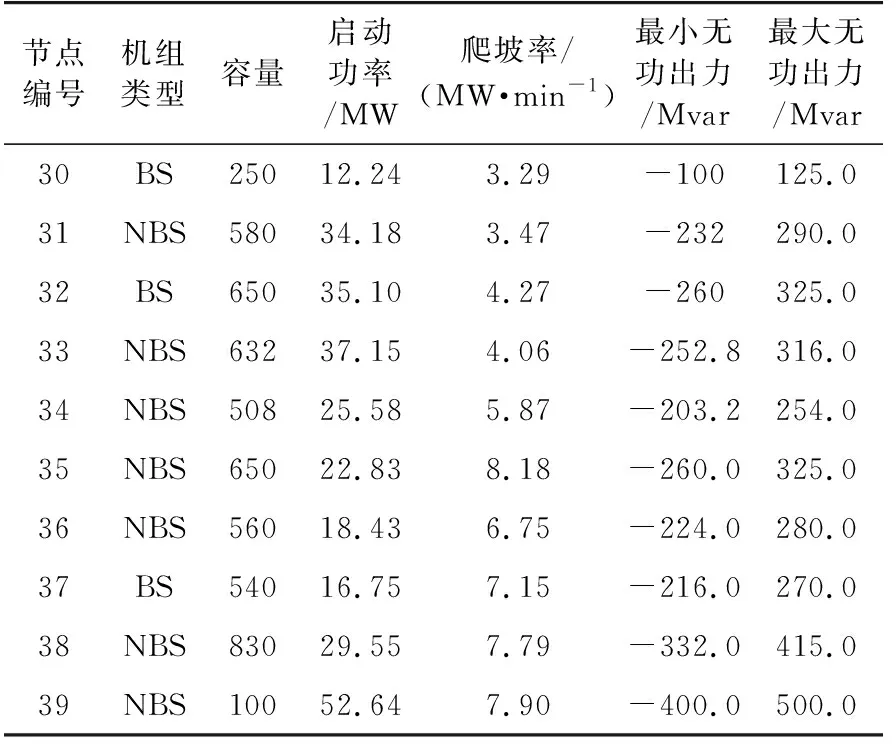
表1 IEEE 39标准测试系统电源启动特性Table 1 The startup characteristics of generators in IEEE 39-bus system

图1 IEEE 39标准测试系统分区结果对比Fig.1 Sectionalizantion results of IEEE 39-bus system for different methods

(1) 基于谱聚类方法，将IEEE 39标准测试系统网络抽象成简单的网络拓扑图，并建造Laplacian矩阵，完全根据电力系统的拓扑特性运用k-means聚类方法对其进行聚类，得到了表2中优化前的分区结果。

(2) 运用遗传算法对IEEE 39标准测试系统进行求解，首先，将所有机组所属分区编号作为编码，并生成20个初始种群，然后运用Dijkstra算法对每个初始种群搜索恢复路径并根据适应度函数计算其适应度值。若初始种群所代表的分区结果使得最后整个系统的恢复时间越短，则这个初始种群的适应度值越高。筛选得到适应度最高的初始种群作为第一代最佳种群，而其余种群通过交叉变异其中几个机组的所属分区编号得到不同的20个种群，不断迭代重复上述过程，直至得到最后的最佳种群即最优分区方案。文中设置迭代次数为100次。

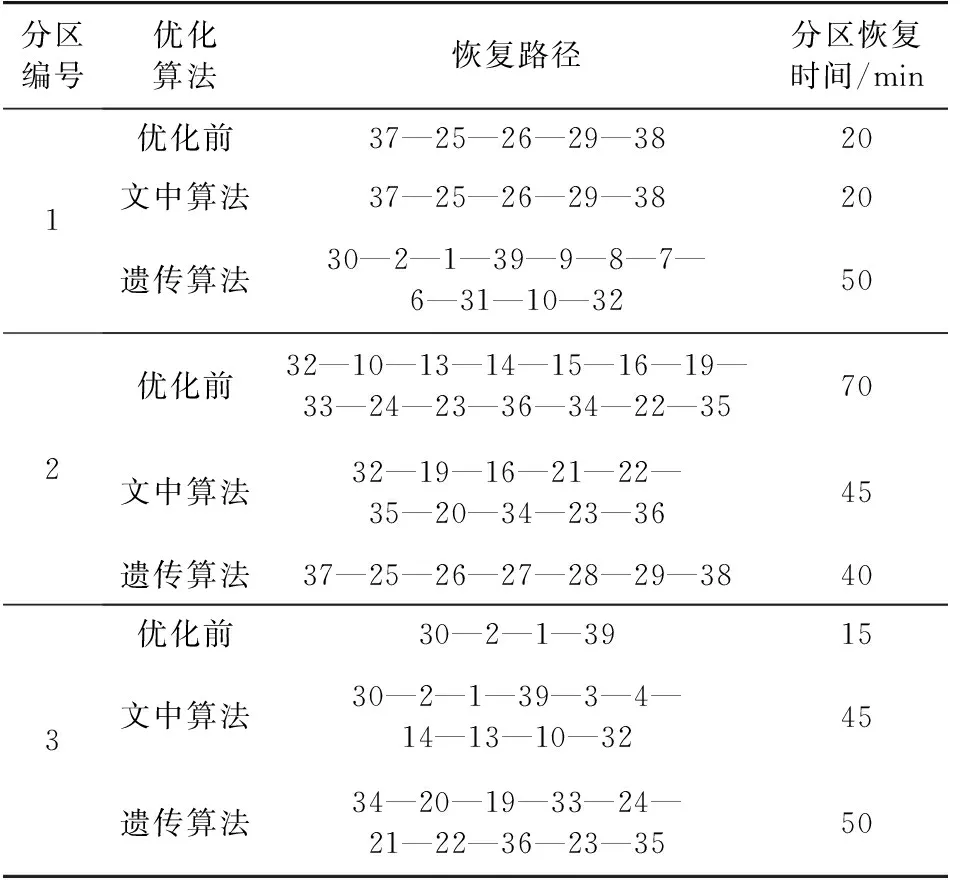
表2 IEEE 39标准测试系统分区恢复优化结果对比Table 2 Restoration results of different subsections withdifferent partition methods of IEEE 39-bus system

(3) 文中方法，以运用谱聚类得到的优化前分区结果为基础进行优化。首先运用粗糙集的理论方法，按照式(13)确定不确定度μ，并根据初始分区结果确定重要度imp和误差δP和δN，建立带有不确定因子的决策表，如表3所示。并根据初始分区结果，确定误差为δp=0.5和δN=0.5，所以需要尝试调整的机组集合为{33,34,35,36}。因为测试系统较小，所以确定最终调整机组个数为1，并对筛选出的机组集合内的机组进行遍历调整，选择最优的调整方案。

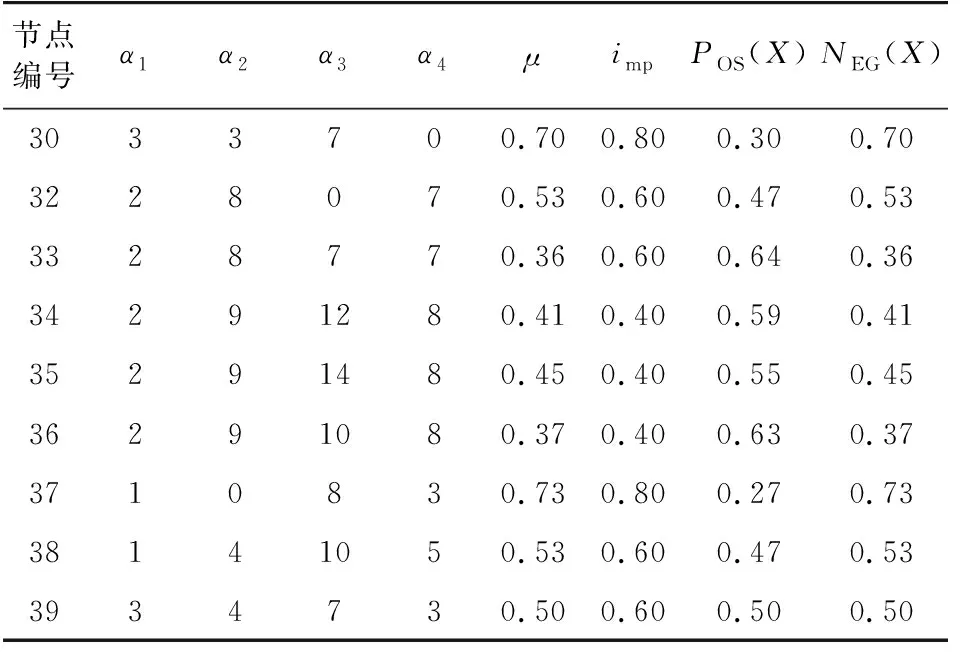
表3 IEEE 39标准测试系统决策表Table 3 Decision table of IEEE 39-bus system

由图1可见，实线代表的基于谱聚类方法的初始分区结果中3个分区的大小不均衡，红色分区明显小于黄色分区。虚线代表的优化后的分区结果中，黄色分区中的一部分线路和机组被调整到了红色分区中，从而3个分区的大小更加均衡。3个分区所需的恢复时间可更加直观列于表2，可知运用谱聚类方法得到的分区结果及恢复时间为20 min，70 min，15 min，遗传算法所得结果为50 min，40 min，50 min，最后文中算法所得分区恢复时间为20 min，45 min，45 min。从优化前的结果可见，仅仅依赖系统拓扑特性得到的分区大小差异较大，率先恢复完成的分区需要等待55 min，待所有分区均恢复完成后才能进行并网，系统恢复效率低，因此仅仅依靠谱聚类方法得到的分区结果需要进行优化。而经过文中算法优化后，分区间仅仅需要等待25 min，分区的大小相比优化前更加均衡，而且系统所需要的总恢复时间也大大缩短，可见文中优化有效。

而遗传算法的结果与文中算法结果相比，显然遗传算法得到的分区大小更加均衡，分区之间恢复时间差为10 min，而文中算法所得结果的恢复时间差为25 min。但是系统的总恢复时间较长，而且遗传算法所用计算时间为2 050.758 s，远大于文中算法所用时间18.9 s。导致这个结果的原因首先是遗传算法在生成初始种群时的随机性，并未考虑网络的拓扑特性，故同一个分区中的待恢复机组可能相距较远，需要较长的恢复时间。虽然通过增加迭代次数，遗传算法得到了较文中算法更加优化的分区结果，但是计算时间更长，同样会拖慢电力系统的恢复进程。与其相比，文中算法大大降低计算复杂度，缩短了计算时间。

4 结语

电力系统分区策略不可忽略系统后续恢复过程中的诸多因素对其分区结果的影响。文中在运用谱聚类算法实现初步分区的基础上，以系统最短恢复时间为目标建立了分区优化模型，并运用基于粗糙集的带有不确定度的决策表对需要调整的机组进行筛选，提高了分区优化速度，得到优化后的分区结果和系统恢复时间。IEEE 39算例证明了文中优化算法的有效性，且该算法具有较高的求解效率。

后续研究将着力于研究优化后得到的最优分区结果和最短系统恢复时间，使其能够考虑到文中方法在筛选时有可能忽略的最优分区结果。

本文得到云南电网公司科技项目“在自然灾害下电网风险评估与预防控制技术研究二期工程”，宁夏电网公司科技项目“电网一体化安全管控体系平台技术支撑系统”及智能电网保护和运行控制国家重点实验室开放课题研究项目资助，谨此致谢！