基于PSO-Newton法的电-气综合能源系统能流计算

闵庆久， 马兆兴， 马英姿

(青岛理工大学信息与控制工程学院，山东 青岛 266520)

0 引言

能源是社会经济发展的重要支撑。近几年随着煤炭、石油等传统能源的日益枯竭以及人们对发展绿色经济的要求，探索清洁无污染的能源与提高能源的综合利用效率成为了当今社会研究的热点[1—3]，于是综合能源系统(integrated energy sys-tem,IES)的概念应运而生。

IES加强了以往各自独立的电力系统、天然气系统和供热系统之间的耦合，并对各种能源的生产、运输和消费等环节进行了集成与优化，大大提高了能源的利用效率[4—7],是未来能源发展的主要方向。天然气与其他化石燃料相比，具有储量丰富、低碳环保等特点，并且随着电解制取天然气(power to gas,P2G)技术的发展与燃气机组的并入电网[8]，电-气2个系统之间的耦合成为了IES研究的一个重要方面。

能流计算作为电-气IES研究的基础与核心，国内外相关学者对其进行了大量的研究。文献[9]在分析天然气系统中压缩机不同控制模式的基础上，提出实用化的改进方法，并建立IES的能流计算模型；文献[10]考虑了电-气IES中的不确定因素，提出IES概率能流的概念；文献[11—15]研究了电-气系统的一体化问题，为能使IES运行在最优的状态下，将天然气系统中的暂态气流与电力系统中的稳态潮流相结合，提出最优能流计算方法,得到电-气一体化系统的最优动态能流；文献[16]介绍了电-气-热3个系统之间的耦合单元以及各个系统间物理特性的不同，并基于此给出了2种新型交替迭代的能流计算方法；文献[17]基于天然气系统的暂态模型，对电-气IES进行多时段的能流仿真；文献[18]考虑了温度对整个电-气系统能流计算结果的影响；文献[19—20]通过研究不同的能源设备及能源供应条件，提出4种不同模式下的IES能流计算方法。目前关于牛顿(Newton)法中对天然气系统节点压力初值选取问题的研究尚浅，文献[21]利用工程经验来确定压力初值，但这样误差较大；文献[22]在求解时考虑将未知的节点压力设为0，但在求解过程中可能会出现雅可比矩阵奇异的情况。

文中利用粒子群(partical swarm optimization,PSO)算法的全局搜索能力解决了天然气系统Newton法压力初值选取困难的问题，并采用顺序求解法在IEEE 14节点配电系统和14节点的天然气系统中分2种耦合模式验证了所提方法的可行性。

1 电-气IES数学模型

1.1 电力系统数学模型

电力系统中节点电压的表达方式分为直角坐标和极坐标2种[23—24]，文中采用的是极坐标方式，其表达式为：

(1)

节点的功率表达式为：

(2)

(3)

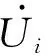
1.2 天然气系统数学模型

在天然气系统中，2个节点间的管道流量可以表示成与节点压力有关的函数，其具体形式为：

(4)

式中：fij为管道ij间的天然气流量；pi，pj分别为节点i，j的压力；kij为与天然气管道的直径、摩擦系数、长度、温度等因素有关的常数；sij为天然气管道中的天然气流动方向，如式(5)所示：

(5)

由于摩擦阻力的存在，天然气在管道运输的过程中必然会有一定的压力损失，所以需要利用压缩机来提升管道中的压力以弥补这些损失。压缩机分燃气驱动和电驱动2种方式，文中采用燃气驱动的压缩机，其简易模型如图1所示。

图1 简易压缩机模型Fig.1 Simple compressor model

燃气压缩机消耗的等效功率与出入口侧的压力比、流过压缩机的天然气流量的关系可以表示为：

(6)

式中：Pc为压缩机的功率；Bc，Zc为压缩机参数；r为气体绝热指数，取1.3[25—26]；fc为流过压缩机的天然气流量。

压缩机消耗的天然气流量与功率间的关系为：

(7)

式中：fτ为压缩机消耗的天然气流量；α，β，λ为能量转换效率常数，文中取α=λ=0，β=0.2×10-3。

天然气系统中的节点满足流量平衡，即任一节点流入的天然气流量等于流出该节点的流量，用方程表示为：

(8)

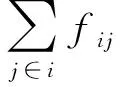
1.3 电-气互转数学模型

气转电指的是燃气轮发电机以天然气作为燃料进行发电，其消耗的天然气量与发电功率的关系为：

(9)

式中：PG2P为燃气轮机的发电功率；fG2P为燃气轮机消耗的天然气量；Φ，φ，μ为天然气驱动燃气轮机的能量转换系数；fGHV为天然气高热值。

电转气指的是电解制取天然气，制取天然气的过程可以分为2个步骤。首先是电解水产生氢气，然后通过Sabatier反应将氢气与二氧化碳转化为甲烷，即天然气的主要成分[27]，电解制取天然气消耗的电能与输出天然气量关系为：

fP2G=ηP2GPe

(10)

式中：fP2G为电转天然气设备输出的天然气量；ηP2G为电转天然气设备的效率；Pe为电转天然气设备功率。

2 电-气能流计算模型

2.1 Newton法

Newton法是一种给定初值，然后通过一步步迭代寻找最优值的方法。其中电力系统的迭代方程为：

(11)

(12)

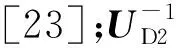
根据式(4)得到天然气系统中的管道流量可以表示成与节点压力有关的函数，因此天然气系统的迭代方程为：

(13)

Δf=-JgΔp

(14)

其中：

(15)

式中：Jg为天然气系统的雅可比矩阵，如式(16)所示。

(16)

2.2 PSO算法

PSO算法是在受到鸟群觅食的启发后发展起来的一种智能优化算法，粒子群中的每个粒子通过跟踪比较目前自己找到的最优值和整个种群找到的最优值来更新自己。每个粒子的位置与速度更新方程为：

(17)

式中：vid，xid分别为粒子的速度与位置；w为惯性因子，取0.6；c1，c2为学习因子，取2；ξid为第i个粒子本身找到的最佳位置；r1，r2为[0,1]间的随机数；ξgd为整个种群找到的最佳位置。

2.3 电-气能流计算流程

文中在气转电和电转气技术的基础上提出“以气定电”和“以电定气”2种耦合模式以验证所提方法，2种模式下的计算流程分别如图2和图3所示，其中模式一为“以气定电”模式，模式二为“以电定气”模式。

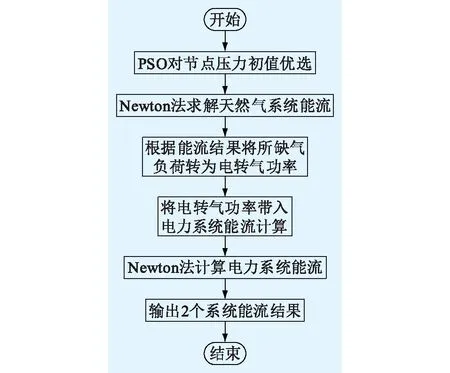
图2 模式一能流计算流程Fig.2 Energy flow calculation process of model 1

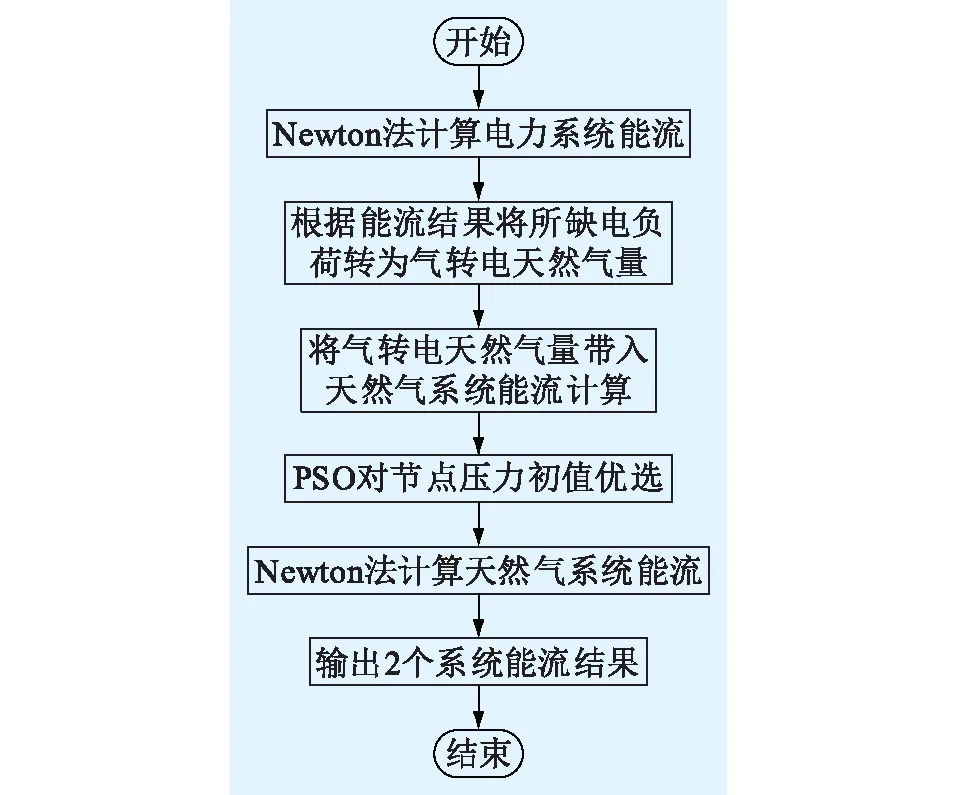
图3 模式二能流计算流程Fig.3 Energy flow calculation process of model 2

3 算例分析

文中所提方法利用Matlab在IEEE 14节点配电系统和14节点天然气系统上进行了验证，使用的计算机CPU配置为Intel(R) Core(TM) i5-5200U,主频为2.2 GHz，其中所使用到的天然气系统气负荷见表1，其余具体参数可以参考文献[10]。配电系统与天然气系统的结构示意分别见图4和图5。

表1 天然气系统气负荷Table 1 Gas loads of natural gas system

图4 IEEE 14节点配电系统Fig.4 IEEE 14-bus power distribution system

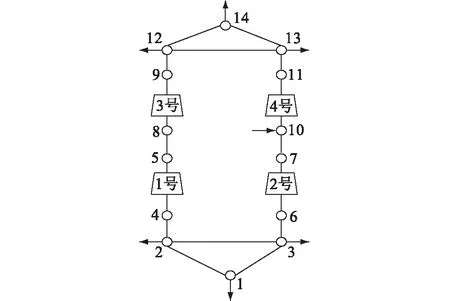
图5 14节点天然气系统Fig.5 14-node natural gas system

关于天然气系统中压缩机的控制方式有定升压比、定出口压力、定入口压力3种，在文中所使用的4台压缩机中，使用定升压比控制的压缩机为1号和2号，3号与4号压缩机控制方式分别为定入口压力和定出口压力，其详细数据见文献[10]。鉴于天然气系统中压力初值难以选取的问题，首先将节点流量的不平衡量转化为一个最值问题，即：

(18)

式中：ψ(p)为所有节点天然气流量不平衡量的均值。将ψ(p)作为目标函数带入到PSO迭代程序中求得最小值，此时的节点压力即为Newton法中的初值。文中分别研究迭代次数和种群规模2个方面对最终目标函数值的影响，首先种群规模定为50，迭代次数分别为50，100，500，1 000，ψ(p)的数值与迭代次数的关系如图6所示。

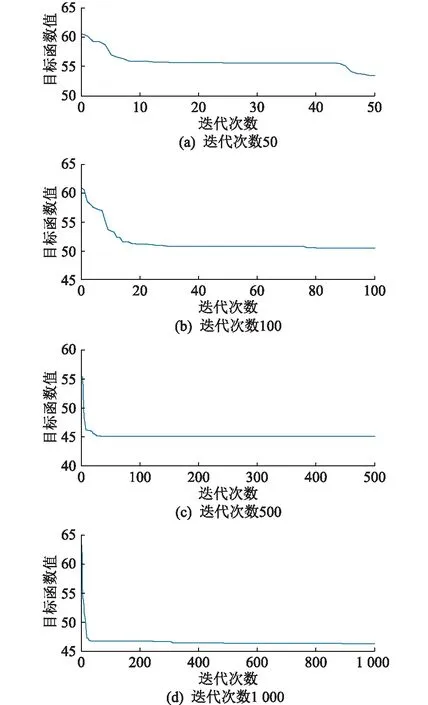
图6 目标函数值与迭代次数Fig.6 Objective function and iteration times

PSO算法作为一种随机最优算法，在迭代伊始每个粒子的速度与位置都是随机的，并且每个粒子都具有记忆特性，所以每次迭代的结果不一定完全相同，这与图6中的结果相吻合。由图6可以看出，在迭代的初始阶段，目标函数值随着迭代次数的增加而迅速减少，但在经过一定的迭代次数后目标函数值的取值趋于平缓，500次的迭代结果与1 000次的迭代结果相差很小，因此文中迭代次数定为500次，在此基础上更改粒子群的种群规模，分别为20，100，ψ(p)的数值与种群规模的关系如图7所示。

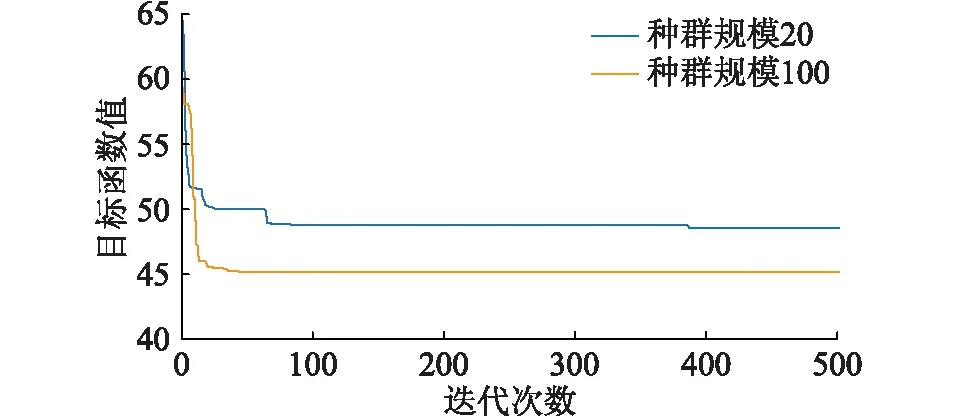
图7 目标函数值与种群规模Fig.7 Objective function and population size

由图7可见，与迭代次数相比，种群规模的大小对最终目标函数值的影响并不大。根据图6与图7可知，天然气系统流量的不平衡量经过PSO程序明显减少，此时得到的节点压力更接近Newton法需要的初值。因此文中采用PSO程序中迭代次数为500，种群规模为50的结果作为Newton法迭代中的初值。

“以气定电”模式是利用P2G设备补足天然气系统所缺天然气负荷，“以电定气”模式是利用燃气轮机补足配电系统所缺电力负荷。“以气定电”模式中P2G设备位于天然气系统的13号节点与电力系统的12节点，“以电定气”模式中燃气轮机位于配电系统的14号节点与天然气系统的3号节点，其耦合示意如图8所示。

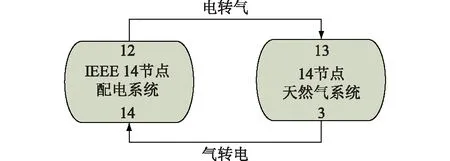
图8 电-气耦合示意Fig.8 Schematic diagram of power-gas coupling

在IEEE 14节点配电系统中，1号节点为平衡节点，2，3，6，8号节点为PV节点，其余节点为PQ节点，除耦合节点外2个系统的其他节点负荷均不作改变。2种模式下的电力系统节点电压、天然气系统节点压力与管道流量分别见图9、图10和表2。

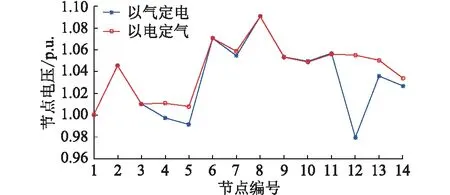
图9 电力系统节点电压Fig.9 Power system nodes voltage

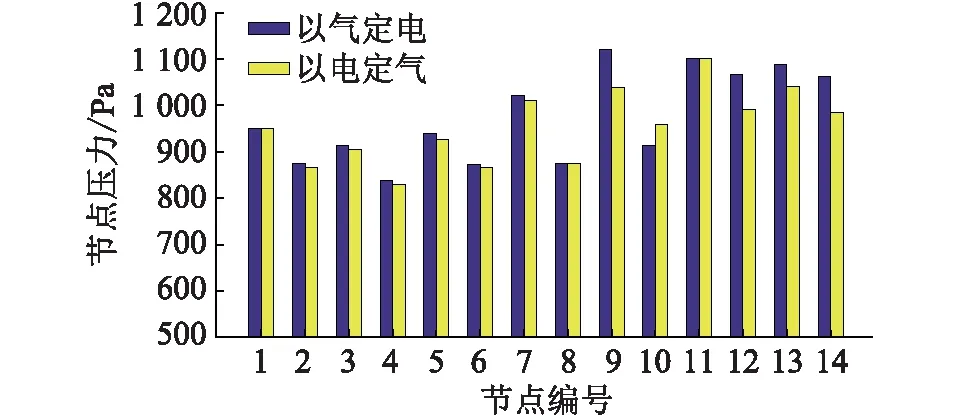
图10 天然气系统节点压力Fig.10 Gas system nodes pressure

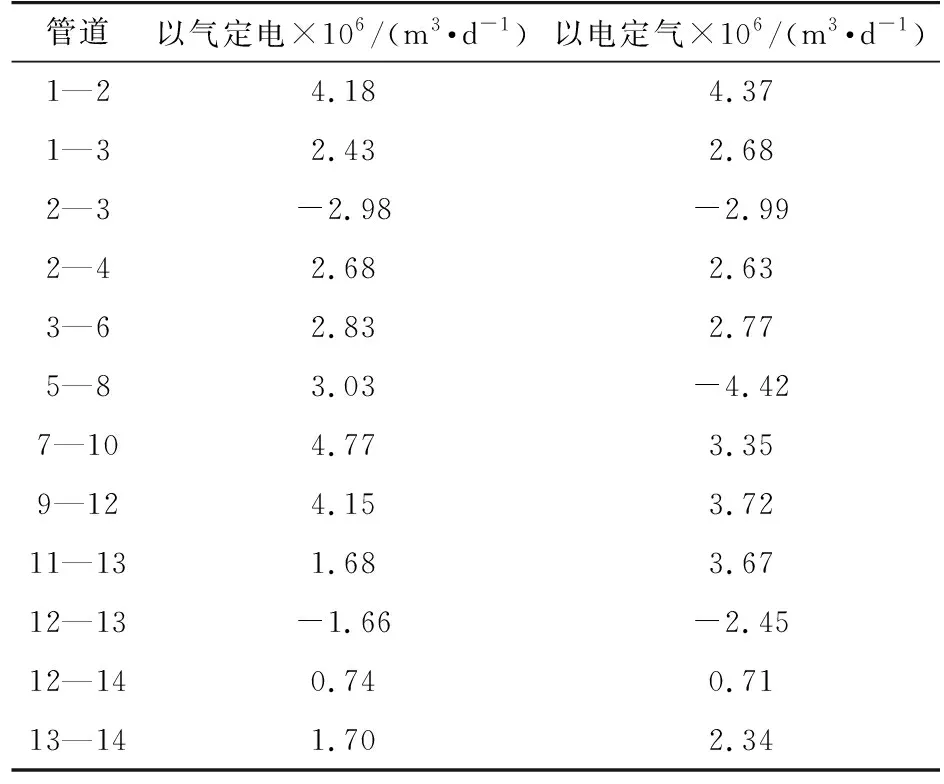
表2 天然气管道流量Table 2 Natural gas flows at pipelines

文中Newton法中的收敛精度为10-4，在“以气定电”模式下，将在PSO中得到的压力初值代入Newton法中计算经过8次迭代达到了收敛要求，所用时间为2.942 s；“以电定气”模式下的迭代次数为6次，所用时间为2.399 s。由图9可知，在“以气定电”模式下的部分节点电压要低于“以电定气”模式下的电压，特别是在耦合节点处下降的尤为明显，这是因为“以气定电”模式下为了满足天然系统的用气需求增加了配电系统的负荷，所以导致了部分节点的电压有所下降。在图10中，“以电定气”模式下的天然气系统节点压力普遍略低于“以气定电”模式下的压力，这与配电系统中节点电压的情况类似，“以电定气”模式下为了满足配电系统中的电力需求增加了天然气系统的气负荷，天然气消耗量增大，从而导致节点压力下降。

分析图9和图10的能流结果可知，这2种模式所适用的场合并不相同，须因地制宜。“以气定电”模式适用于电力资源较丰富的地区或时段，例如，风能作为一种非常理想的可再生能源，发展前景十分广阔，但受风力的影响较大，在某一段时间内风力充足时[28—29]，弃风现象严重，若这段时间内风力发电所产生的富余电能加上天然气储气装置就能够很好地实现配电系统的“削峰填谷”；“以电定气”模式适用于天然气资源较为丰富的地区，天然气作为一种清洁能源，能够有效缓解煤炭资源紧张及环境污染问题。

4 结论

文中以电-气IES能流计算Newton法中天然气系统的初值难以选取为切入点，提出先利用PSO法对天然气系统初值进行优选，然后结合Newton法进行能流计算，可以得到以下2个结论：

(1) 文中基于电转气和气转电技术分“以气定电”和“以电定气”2种模式提出PSO-Newton法，根据算例结果验证了所提方法在小规模天然气系统中的有效性，计算速度较快，并且具有良好的收敛特性。

(2) 这2种耦合模式可以根据所在地区与时段不同视情况选取，具有很强的灵活性，若2个系统间配有一定的储能设备则可以有效提高不同能源之间的利用效率，减少传统化石能源对环境的破坏。

然而在大规模气网中有的管道流向复杂，在能流计算前难以确定，今后将研究该方法对更大规模、管道流向未知时天然气网络的适用性。