超胞声子晶体板的轻量化设计与研究

郭兆枫，陈传敏，乔钏熙，倪 园

(1.华北电力大学环境科学与工程系，河北省燃煤电站烟气多污染物协同控制重点实验室，保定 071003；2.华北电力大学，区域能源系统优化教育部重点实验室，北京 102206；3.中国电力科学研究院有限公司，武汉 430074；4.中国电力科学研究院有限公司,电网环境保护国家重点实验室,武汉 430074)

0 引 言

随着社会发展，社会用电量逐年递增，相应的变电站建设随之增多。由此带来的噪声污染已经对变电站附近居民产生了极大影响，同时，也会对电网的建设产生一定的影响。变电站的噪声由于其频谱具有低频且峰值稳定的特性，导致常规材料对其噪声进行控制时，或特别笨重或无法对其有效降噪。例如现有应用于变电站降噪的技术手段基本上采用BOX-IN的方法，其基体充斥着很厚的钢板，导致安装十分繁琐费力，且对低频噪声的隔声效果一般。另一种针对变电站降噪的常用结构为微穿孔板，虽然重量较轻，但需要很厚的空腔才能发挥其性能，因此也需要占用大量空间。而声子晶体不仅可以根据所需调控其带隙，并且可通过局域共振使带隙突破质量定则。因此，使用声子晶体这种新型人工超材料对变电站噪声进行控制具有很强的针对性及适用性。

声子晶体是作为光子晶体这一概念的类比而提出的。1992年，Sigalas和Economou[1]首次在理论上证实了将球形材料埋入某一基体材料后形成的周期性点阵结构具有带隙特性，并在金、铅球与铝或者硅基体所形成的复合材料结构中同样证实了带隙的存在。1993年，Kushwaha等[2]通过采用平面波方法对镍柱在铝合金基体中形成的复合结构进行计算，获得了声波带隙，进一步明确提出了“声子晶体”的概念——它是由两种或两种以上的弹性介质材料周期性排列成的能够展示出声学带隙或禁带的人工复合型结构。

声子晶体带隙产生的机理源于布拉格散射机理和局域共振机理[3-6]。在基于布拉格散射的声子晶体结构中，声波被周期性排列的散射体所散射，使得在某段特定入射频率的声波经散射后产生相位相消，最终导致该频率范围内的声波或弹性波无法透过该声子晶体，这个范围就叫做带隙[7]。而在局域共振型结构中，带隙可以出现于波长远大于晶格常数的频率区域，由于相比布拉格散射型具有明显的低频隔声优势，因此常选择局域共振型声子晶体应用于低频噪声控制工程[8-11]。

Wu等[12]应用有限元方法(FEM)分析双基局部共振声子晶体(LRPC)的带隙特性时，考虑了晶胞数量、基板的曲率和边界约束等应用的关键因素。结果表明，具有小曲率和边界约束的非无限双基LRPC结构仍然可以产生预期的带隙。并且使整个晶体的振动水平急剧降低了15 dB，内部噪音也降低了9 dB。Zuo等[13]研究了具有双基板的LRPC。结果表明，上下板之间的结构不对称有利于降低导通频率，有效增大带隙。秦浩星等[14]通过建立声子晶体负泊松比蜂窝基座的等效动力学模型,研究该基座局域共振减振机理。研究结果表明，当声子晶体固有频率与基座固有频率接近时，能有效降低基座发生结构共振时的响应幅值。最终建立了声子晶体蜂窝基座的优化设计模型，该模型能够有效抑制结构的低频共振现象。舒海生[15]等提出了一种局域共振型角式声子晶体梁，采用传递矩阵法进行了理论分析和数值求解,并进一步在有限元软件中做了仿真验证，结果表明该角梁能够通过纵波与横波的转换，使得三个自由度上的振动均能在同一频带内得到有效衰减，一方面满足了工程上的多维减振需求，另一方面也拓展了声子晶体减振应用场合。综上所述，常规局域共振型声子晶体板由于基于能带理论和局域共振理论，在带隙频率降低的过程中，散射体的尺寸也相应增大，使常规声子晶体隔声板在控制变电站等低频噪声时，没有体现出应有的质量更轻、隔声效率更高等优势，给其工程应用及发展带来诸多限制与困扰。

为了解决这个问题，本文提出一种局域共振型声子晶体板的轻量化设计方法，根据变电站噪声频谱特性，对声子晶体板进行超胞复合。本文设计的轻量化超胞声子晶体板不仅在带隙上匹配变电站噪声频谱特性，而且在重量及尺寸上相比其他局域共振型声子晶体大大降低。为今后变电站的噪声控制提供了一种轻质的降噪超材料，同时对局域共振型声子晶体的轻量化设计提供了新思路与方法。

1 声子晶体的轻量化设计方法

首先，在确定材料组成后建立能带计算模型与声传输损失(STL)仿真模型。使波矢K在倒格矢空间上扫略过不可约布里渊区的高对称点(Γ-X-M-Γ)，便可计算得到能带图。其中，能带计算模型及其不可约布里渊区如图1所示。

图1 能带计算模型及其不可约布里渊区

之后选取隔声仿真模型包含的元胞数。本文对1个元胞、2×2个元胞、3×3个元胞、4×4个元胞及5×5个元胞构成的模型进行隔声频谱与能带对应验证，如图2所示。发现1个元胞及2×2个元胞的对应关系不够匹配，而3×3个元胞已达到十分匹配的结果，再增加单元数对结果影响不大且会增大计算量，降低计算效率。同时，周期性边界条件下的隔声仿真也显示出与3×3个元胞一致的结果。由于实际工程中不存在无限周期性结构，为了指导下一步的工程应用，因此选择3×3个元胞作为隔声仿真研究对象。

在能带计算模型中，通过类改性方法，计算该结构下局域共振性能最大的包覆层半径与散射体半径之比。定义元胞尺寸a=66.67 mm，板厚h=10 mm，包覆层外半径R1=30 mm。散射体的半径R2为变量，以0.1 mm为步长，令R2从28 mm到2 mm进行参数化计算其能带。得到当R2=14.1 mm时，该结构的第一完全带隙起点达到最低40.695 Hz，即此时局域共振性能达到最大，如图3所示。计算其包覆层半径与散射体半径之比为R2/R1=0.47。并做R2=14.1 mm时声子晶体板的能带图，如图4所示。图中共计算了10阶能带，包含了两个X-M方向的方向带隙与一个完全带隙。由于完全带隙具有更优秀的声学性能，因此对完全带隙进行分析。发现完全带隙的上下边界分别由第3阶和第6阶能带构成，频率范围为40.695～47.233 Hz，带宽约7 Hz。在带隙中存在两阶平直带，即第4阶和第5阶，由于平直带体现的是声子晶体板的共振特性，因此对完全带隙不存在切分的影响。

图2 不同元胞数下能带与隔声对应关系

图3 带隙起点频率随R2变化曲线

在隔声量仿真模型中，定义元胞尺寸a=66.67 mm，板厚h=10 mm，包覆层外半径R1=30 mm。散射体的半径R2为变量，以0.1 mm为步长，令R2从28 mm到2 mm进行参数化计算隔声量。发现其隔声峰值对应的频率值随着散射体半径的减小以及包覆层厚度的增加，呈现出先减小再增大的趋势。与能带显示出同样的规律，验证了本文方法的正确性。

作隔声峰值频率与隔声量随R2变化曲线，如图5所示，发现轻量化声子晶体的隔声频率为该元胞尺寸下的最低频(33 Hz)，且隔声量效果大于70 dB。为同系列声子晶体中质量最轻，兼有良好降噪效果的声子晶体隔声板，说明轻量化设计后声子晶体板的局域共振性能得到最大释放。

2 超胞声子晶体板的结构

对变压器类设备进行声压级测量，并通过傅里叶变换得到其频谱图，如图6所示。确定需要设计的声子晶体隔声频率值。通过频谱图可看到峰值主要集中在50 Hz、100 Hz、200 Hz和400 Hz，由于频率越低波长越长，其衰减更小、危害更大，因此选择50 Hz和100 Hz作为超胞声子晶体板的设计频率。

图4 R2=14.1 mm时能带图

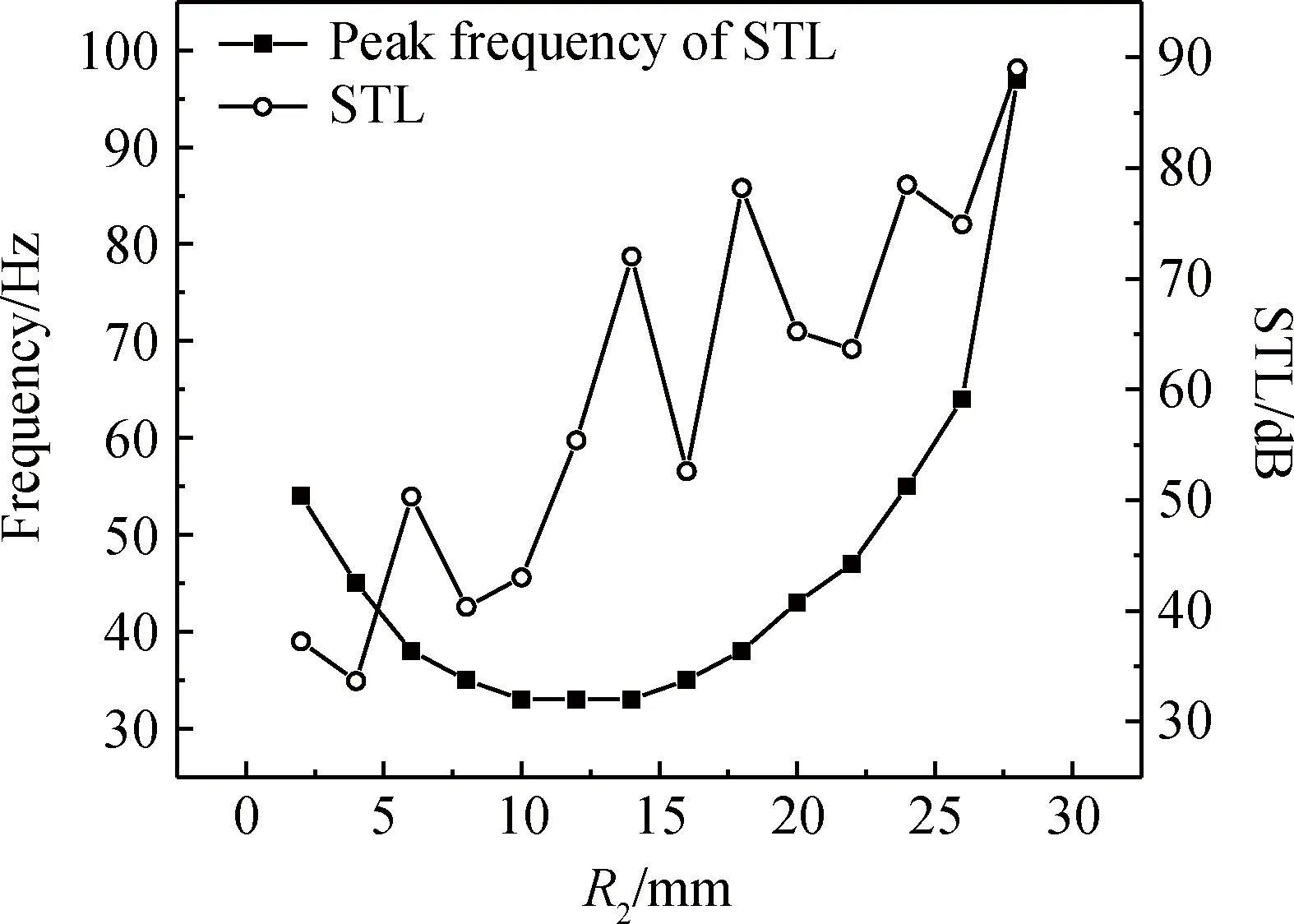
图5 声传输损失峰值频率与声传输损失随R2变化曲线

图6 变压器声压级频谱图

本文设计的超胞声子晶体板的基质由环氧树脂制成，包覆层为硅橡胶，散射体为金属钨。材料参数如表1所示。为了使声子晶体板更加轻薄，定义元胞尺寸a=66.67 mm，板厚h=5 mm，包覆层外半径R1=30 mm。通过能带理论及轻量化声子晶体数值仿真方法，使波矢K扫略过元胞的不可约布里渊区后得到当R2=15.9 mm时，该结构的第一带隙起点达到最低，即此时局域共振性能达到最大。计算其包覆层半径与散射体半径之比R2/R1=0.53。

表1 材料参数

为了确定隔声峰为50 Hz时的几何参数，在保持元胞尺寸a，板厚h不变的基础上，对50 Hz模块的包覆层外半径r1和散射体半径r2进行参数化计算。保持r2/r1=0.53，以0.01 mm为步长，令r1从30 mm到2 mm进行参数化计算其隔声量。得到当r1=15.60 mm，r2=8.268 mm时，在50 Hz出现隔声峰。为了确定隔声峰为100 Hz时的几何参数，保持元胞尺寸a，板厚h不变，对100 Hz模块的包覆层外半径r3和散射体半径r4进行参数化计算。保持r4/r3=0.53，以0.01 mm为步长，令r3从30 mm到2 mm进行参数化计算其隔声量。得到当r3=7.72 mm，r4=4.092 mm时，在100 Hz出现隔声峰。最后将50 Hz与100 Hz的几何参数进行复合。通过数值仿真方法，设计了一种共价八元环结构。由于结构的复合会产生模态的变化，因此需要对几何参数进行微调。最终得到当50 Hz模块与100 Hz模块间距l=33 mm，r1=15.6 mm、r2=8.268 mm、r3=7.85 mm、r4=4.16 mm时，轻量化超胞声子晶体板同时在50 Hz及100 Hz具有明显的隔声峰。超胞有限结构如图7所示。

图7 超胞有限结构

3 声传输损失

STL仿真模型如图8所示。从上到下分别是完美匹配的层(PML)、入射区、材料区、出射区和PML。可以通过公式(1)获得STL。

(1)

其中，P1是入射区的声压，P2是出射区的声压。

通过图9可知，本文设计的轻量化超胞声子晶体板排在前二的声传输损失峰分别出现在50 Hz和100 Hz，其中50 Hz处的声传输损失为67 dB，100 Hz处的声传输损失为48 dB。同时，在92 Hz处也出现了一个声传输损失为43 dB的峰值。判断原因为复合后造成固有模态增多，使其在声波激励作用下的模态振型更加丰富，进而出现了92 Hz的隔声峰与94 Hz的隔声谷。

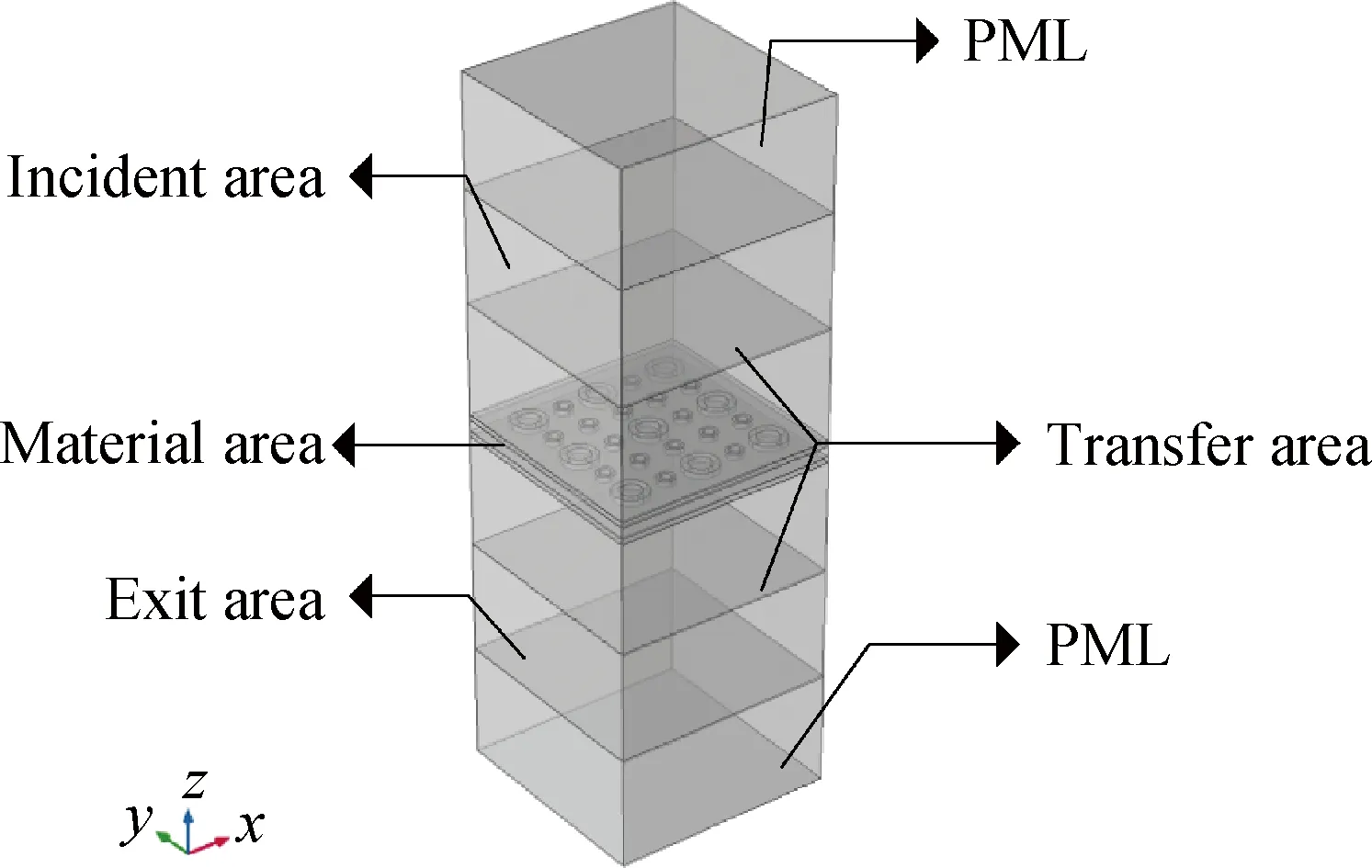
图8 声传输损失仿真模型

图9 声传输损失

4 机理分析

为了研究超胞声子晶体的隔声机理，分别提取50 Hz和100 Hz处的位移变形和声压级复合声强流线如图10所示。(a)、(b)图中的箭头(浅白色)表示固体位移，(c)、(d)图中的箭头(深黑色)表示声强流线。图10(a)是在50 Hz的声波激励下超胞声子晶体的固体表面位移，显示出50 Hz的散射体为最大振幅，同时100 Hz的散射体有轻微的反相位位移。在两种模块的共同作用下，基体板保持不动，使声波无法传播。从图10(c)中可以看到，声波大部分的能量都被反射回去，验证了上述机理。图10(b)是在100 Hz的声波激励下超胞声子晶体的固体表面位移，显示出100 Hz的散射体为最大振幅，同时50 Hz的散射体有轻微的反相位位移，此时的位移相比图10(a)的反相位位移更加微弱。分析原因是由于50 Hz模块的散射体质量更大，所以当其作为主模态共振时，作为副模态的100 Hz模块的散射体更容易被激发并表现出来。当100 Hz模块作为主模态共振时，作为副模态的50 Hz模态的散射体并不容易被激发并表现出来。也可以说，作为副模态的50 Hz模态的散射体只需要非常轻微的反相位振动就可以平衡100 Hz模块的共振，在两种模块的共同作用下，使基体板保持不动，阻止声波的传播。从图10(d)中可以看到，声波大部分的能量耗散在超胞声子晶体板中，验证了上述机理。

通过上述分析，可以发现超胞声子晶体的隔声机理都是由于在某一频率的声波激励下产生了一种主模态共振，这种主模态共振会进一步激发副模态的反相位共振，基体板会在主副模态的一正一反的共同作用下保持不动，从而阻止了声波的传播。

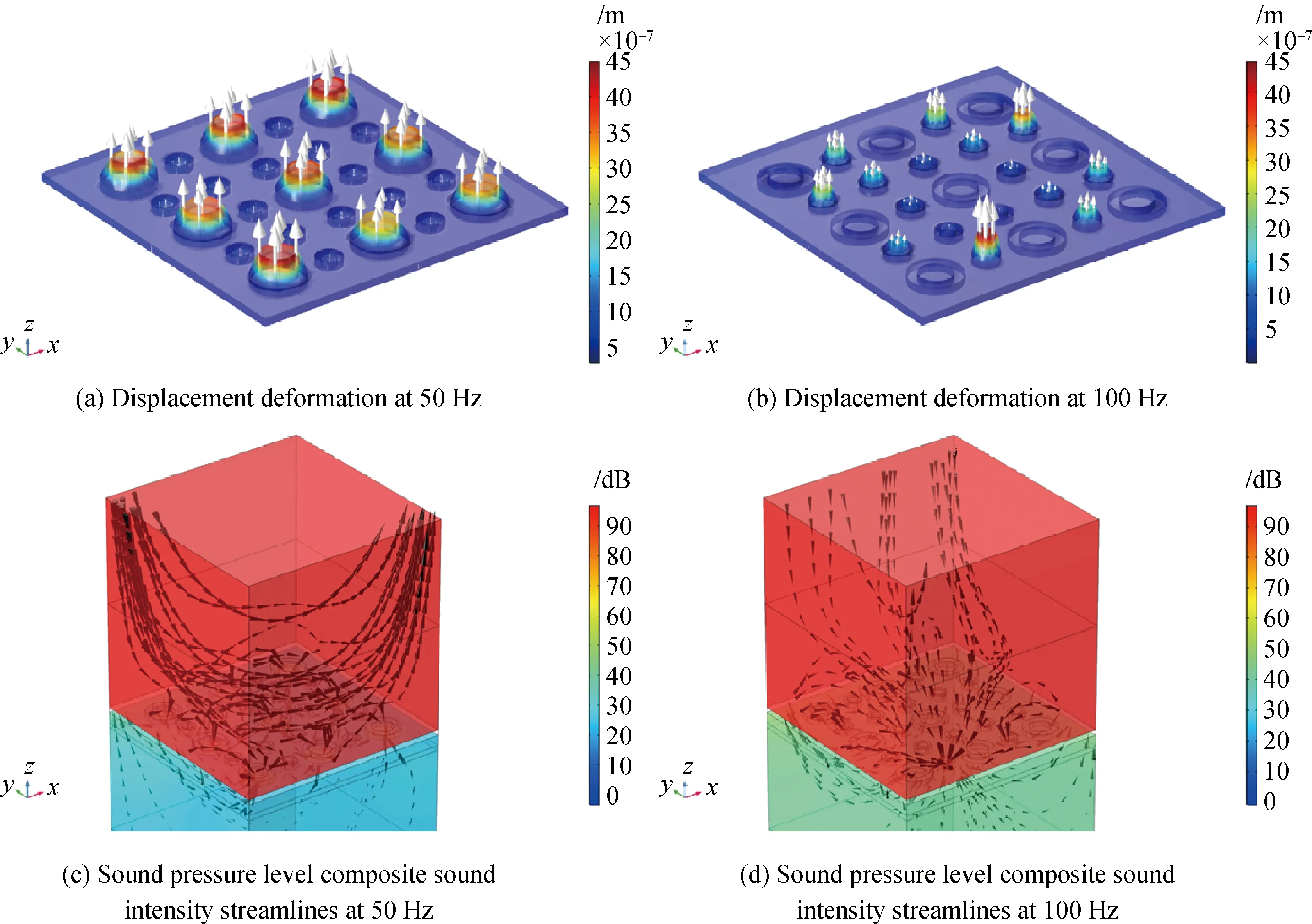
图10 50 Hz和100 Hz处的位移变形和声压级复合声强流线

5 结 论

为了促进声子晶体的工程应用，本文以变电站低频噪声为应用背景，提出一种局域共振型声子晶体板轻量化设计方法。并基于此方法，设计出一种针对变电站噪声频谱特性的轻量化超胞声子晶体板。研究发现，此声子晶体板在50 Hz和100 Hz同时具有明显的声传输损失峰，隔声量分别为67 dB和48 dB。并且由于超胞复合导致声子晶体板的模态增多，使其在声波激励作用下的模态振型更加丰富，从而在92 Hz处也出现了一个声传输损失为43 dB的峰值。并通过振型位移及声压级复合声强流线图对其隔声机理进行了分析研究。发现超胞声子晶体的隔声机理都是由于在某一频率的声波激励下产生了一种主模态共振，这种主模态共振会进一步激发副模态的反相位共振，基体板会在主副模态的一正一反的共同作用下保持不动，从而阻止了声波的传播。

由于变电站噪声的低频特性，一般降噪材料难以达到降噪效果和实际应用效果，而超胞声子晶体板的轻量化设计对于50 Hz和100 Hz同时具有明显的声传输损失峰，具有优良的降噪效果；并且超胞声子晶体板的基质由环氧树脂制成，包覆层为硅橡胶，散射体为金属钨，其材料简单易得。本研究对今后声子晶体板的工程应用和变电站噪声控制都有一定的指导意义。