改进熵权-TOPSIS法的铁路事故定级模糊评价
张正坤,朱昌锋
(兰州交通大学 交通运输学院,兰州 730070)
事故定级作为事故处理过程中的必要环节,对事故整改及预防类似事件再次发生具有现实的指导意义和警示作用[1].目前,有关事故定级的研究主要集中于医疗事故[2]和船舶溢油事故[3]等方面,但对铁路事故定级的研究却相对较少.既有的铁路事故定级方法是以文献[4]中的评价指标和事故等级为依据,根据事故的不同评价指标,确定各指标对应的事故等级,并将最严重的等级作为事故的定级结果.这种定级方法虽然简单且容易执行,但不足之处在于:第一,事故定级过程只将最严重的指标作为评价依据,定级结果不能综合反映事故的严重性;第二,对于指标值在事故等级临界点附近的事故定级过于绝对化,定级结果缺乏合理性;第三,不同事故的严重程度往往有所不同,该方法得到的定级结果可比性较差,不利于事故的量化分析.
铁路事故定级本质上属于多属性决策问题[5].对大部分多属性决策问题而言,指标的属性值虽然是一组精确值,但是属性值与不同方案间的隶属关系通常难以被量化,因此,合理量化二者间的隶属关系是确保决策结果合理性和综合性的关键[6].熵权-TOPSIS法是解决多属性决策问题的一种常用方法.范露华[7]将该方法用于建筑材料供应商的评价问题,蒋丽等[8]将模糊理论与熵权-TOPSIS法相结合,研究了应急物资代储企业的选择问题.指标赋权和方案择优是熵权-TOPSIS法解决多属性决策问题的两个重要环节.其中,熵权法的赋权原理是根据指标的变异程度赋以指标相应的权重[9],其优点在于赋权结果具有较好的客观性,但熵权法在赋权过程中忽略了指标在不同方案上的重要性,因而赋权结果的综合性不强.为此,田俊峰等[10]从指标组合的角度提出了基于条件熵的赋权方法,但该方法并不适合于铁路事故评价,因为铁路事故的评价指标不具有序贯性;南钰等[11]从权重信息和熵值水平一致性的角度对熵权法做了改进,但仍然存在不足.TOPSIS法是根据方案与理想解之间的贴近度而进行排序择优的一种评价方法.盖宇仙等[12]在评价综合运输体系的研究中指出TOPSIS法能够综合多个指标的评价信息,使得评价结果具有较高的可信度;闫欣欣等[13]则认为基于绝对贴近度的TOPSIS法可以消除由理想解变化而引起的逆序现象.
本文利用模糊数学及熵权-TOPSIS法等理论对铁路事故定级问题展开研究.为合理量化指标与不同事故等级间的隶属关系,针对不同的指标界定形式,设计相应的隶属度函数以确保二者间的隶属关系具有良好的模糊性.通过分析熵权法在指标赋权过程中存在极化指标重要性的缺陷,利用灰靶理论中的指标贡献系数对熵权法加以改进,使得指标的赋权结果更具有客观性和综合性.最后,采用基于绝对贴近度的TOPSIS法对铁路事故展开定级评价和分析.
1 事故指标选取及模糊处理
1.1 事故指标选取
铁路事故的评价指标相对较多,考虑到不同的运输性质、运输环境以及指标间的通用性和可量化性等因素,将死亡人数、重伤人数、直接经济损失、机车车辆脱轨数、机车车辆破损数及中断行车小时等作为铁路事故的评价指标,分别用j=1,2,3…,n表示.根据铁路事故的严重程度,将事故由低到高划分成不同的等级,分别用i=1,2,3,…,m表示.
1.2 指标值的模糊处理
根据文献[4]中给定的指标界定形式,将选取的铁路事故评价指标分为(0,a)、[a,b)和[b,+∞)等三种类型.针对不同的指标界定类型,利用模糊数学理论,设计对应的隶属度函数以量化指标在不同事故等级上的隶属关系.
定义1[14]设U为论域,称映射
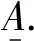
结合定义1,为契合不同的指标界定形式,选取岭形分布函数作为基本隶属度函数以实现指标与事故等级间隶属关系的模糊性[15].据此,对于界定形式为(0,a)类型的指标,设计指标j与事故等级i间的隶属度函数如式(1)所示.
ri,j=
(1)

(2)
式中:λj为指标j在事故定级评价中的跨距,如式(3)所示.
(3)
对于[a,b)类型的指标,设计指标j与事故等级i间的隶属度函数如式(4)所示.
ri,j=
(4)

(5)
对于[b,+∞)类型的指标,设计指标j与事故等级i间的隶属度函数如式(6)所示.
ri,j=
(6)


2 改进熵权法的铁路事故指标赋权
2.1 基于熵权法的指标赋权过程
熵权法是根据指标变异程度赋以指标相应权重以体现其重要性的一种赋权方法[9].相比于其它赋权方法,如层次分析法[16],熵权法因在指标赋权过程中排除了决策者的主观因素,使得赋权结果具有较强的客观性[17].根据指标与事故等级间的隶属度矩阵R=(ri,j)m×n,基于熵权法的指标赋权过程如下:
第一步:隶属度矩阵的规范化处理
根据隶属度矩阵R=(ri,j)m×n,利用式(7)做规范化处理,得到规范化的隶属度矩阵P=(pi,j)m×n.
(7)
第二步:计算指标的信息熵
根据规范化的隶属度矩阵P=(pi,j)m×n,利用式(8)求得指标j的信息熵Hj.
(8)
式中:K=1/lnn;当pi,j=0时,pi,j·lnpi,j=0.
第三步:确定指标的权重值
根据指标j的信息熵Hj,利用式(9)便可得到指标j的权重值wj.
(9)
熵权法的关键在于利用公式(8)计算指标的信息熵来反映指标在不同事故等级上的变异程度,进而体现指标的重要性.但从上述计算过程可以看出,指标的信息熵明显忽略了不同指标对同一事故等级的影响,致使指标的赋权结果具有一定的片面性.例如:给定已规范化的隶属度矩阵P′为
利用熵权法便可求得指标的权重W为
W=[0.007 4 0.193 5 0.799 1].

2.2 基于指标贡献系数的熵权法改进
2.2.1 基于灰靶理论的指标贡献系数计算
灰靶理论是灰色系统理论中的重要内容,其核心是靶心度分析和贡献度分析[18].其中,贡献度分析是通过序列的灰靶变换获取各评价对象在不同模式上的贡献因子,进而根据贡献因子的灰关联差异信息确定二者间的贡献系数,并据此展开影响分析.
鉴于灰靶理论中的贡献度对分析贫信息多属性决策问题具有很好的优势[19],根据式(7)求得的规范化的隶属度矩阵P=(pi,j)m×n,利用贡献系数量化指标对不同事故等级产生的影响或贡献.
第一步:构造序列集合
给定ω(j)={ω1(j),ω2(j),…,ωm(j)}为指标模式序列.对于∀ωi(j)∈ω(j),当1≤i≤m且1≤j≤n时,ωi(j)为规范化隶属度矩阵P=(pi,j)m×n中的元素pi,j,即ωi(j)=pi,j.特别地,令ω(0)={ω1(0),ω2(0),…,ωm(0)}为具有极大极性值的贡献参考序列(又称为靶心),且对于∀ωi(0)∈ω(0),均有
(10)
第二步:序列灰靶变换
为使各指标模式序列与贡献参考序列之间具有一致性和可比性,对构造序列进行灰靶变换.令T为序列的灰靶变换,其变换过程如式(11)所示.
T(ω(j))=x(j)={x1(j),x2(j),…,xm(j)},∀j=0,1,2…,n.
(11)
式中:xi(j)为构造序列经灰靶变换后指标j在模式i上的贡献因子,且
(12)
显然,对于任意∀ωi(0)∈ω(0),ωi(0)对应的贡献因子xi(0)∈x(0),均有xi(0)=1.
第三步:建立灰关联差异信息空间
给定ΔGR={Δ,Δmax,Δmin}为贡献因子集对应的灰关联差异信息空间,其中,Δ表示指标模式序列与贡献参考序列的灰关联差异信息(绝对差),如式(13)所示;Δmax表示二者间灰关联差异信息的最大绝对差,如式(14)所示;Δmin表示二者间灰关联差异信息的最小绝对差,如式(15)所示.
Δi(0,j)=|xi(0)-xi(j)|,∀i=1,2,…,m,∀j=1,2,…,n.
(13)
(14)
(15)
第四步:计算指标贡献系数
根据指标模式序列与贡献参考序列建立的灰关联差异信息空间,便可求得指标j在模式i上的贡献系数qi,j,如式(16)所示.
(16)
式中:α和β为灰关联系数,本文取α=1、β=0.5.
2.2.2 基于指标贡献系数的熵权法改进及其合理性分析
根据指标j在事故等级i上的贡献系数qi,j,针对熵权法在指标赋权过程中存在极化指标重要性的缺陷,利用式(17)和式(18)分别取代式(8)和式(9)以改进熵权法的赋权内涵.
(17)

(18)

为分析改进熵权法的合理性,现对公式(17)做如下推导.
(19)
式中:Hj为传统熵权法求得的指标信息熵,如式(8)所示;ΔHj表示考虑指标贡献系数的信息熵修正值,如式(20)所示.
(20)

3 基于TOPSIS法的铁路事故定级评价


A=(ai,j)m×n.
其中:ai,j为加权隶属度,由式(21)确定.
(21)

第二步:根据加权决策矩阵A,确定正理想解R+和负理想解R-,分别如式(22)和式(23)所示.
(22)
(23)

(24)
(25)
(26)
第五步:根据事故等级i的贴近度Vi,确定其绝对贴近度Ei,如式(27)所示.
(27)
最后,根据事故等级i与正、负理想解间的绝对贴近度Ei,便可对铁路事故进行定级评价.显然,Ei的值越大,事故与等级i越接近,反之则越远.本文将绝对贴近度Ei=1的等级作为事故的综合定级结果.
4 实例应用
4.1 实例介绍
选取六个铁路事故案例作为评价对象.各案例的评价指标及指标值如表1所列,繁忙干线铁路事故等级及指标界定值如表2所列.
4.2 定级结果及合理性分析
结合案例中的具体数据,利用评价指标与事故等级间的隶属度函数和改进熵权-TOPSIS评价方法,通过Python编程并在PyCharm平台上运行,得到不同事故的定级结果如表3所列.另外,为了定级结果的比较分析,表3中同时列出了传统熵权-TOPSIS法和文献[4]得出的定级结果.
表3可以看出,传统熵权-TOPSIS法的定级结果相对比较保守,而文献[4]的定级结果具有一定的片面性.相比之下,改进熵权-TOPSIS法的定级结果较为中肯,更能够综合体现事故的严重性.为进一步分析不同评价方法对事故定级结果所产生的影响,给出不同评价方法得出的绝对贴近度如表4所列.
表4中,改进熵权-TOPSIS法求得的绝对贴近度值比传统熵权-TOPSIS求得的绝对贴近度值更具有离散性,说明改进熵权-TOPSIS法更有利于量化分析事故的严重性.总体而言,改进熵权-TOPSIS法得出的事故定级结果略有偏重,但该结论不具绝对性,因为传统熵权-TOPSIS法将事故5定级为重大事故,而改进熵权-TOPSIS将其定级为较大事故,且求得的绝对贴近度也明显不同.结合传统熵权法和改进熵权法的赋权原理可以推断,这主要是由于事故5的指标变异程度及其对不同事故等级的影响不同而导致的.鉴于事故5的特殊性,根据事故5的指标值,给出指标值在不同事故等级上的隶属度如表5所列.

表1 案例中的评价指标及指标值

表2 繁忙干线铁路事故等级及指标界定值

表3 不同事故的定级结果

表4 不同评价方法得出的绝对贴近度

表5 事故5中指标值在不同事故等级上的隶属度
根据表5中的指标值在不同事故等级上的隶属度,利用改进熵权法和传统熵权法得到事故5的评价指标权重值如图1所示.

图1 事故5的评价指标权重值Fig.1 Weight values of evaluation indexes in accident 5
结合表5和图1可以看出,由于直接经济损失(指标5)的变异程度最大,传统熵权法赋以该指标较大的权重,约为0.618 6,这是导致传统熵权-TOPSIS将事故5定级为重大事故的主要原因.但是,由于直接经济损失对其它事故等级产生的综合影响较小,改进熵权法将其赋权为0.141 3,从而避免了该指标权重的极化现象.改进熵权-TOPSIS将事故5定级为较大事故,且与重大事故的贴近度约为0.715 3,从表5中的隶属度可以看出,该定级结果具有一定的合理性.因此,改进熵权-TOPSIS更适合于事故定级评价.
公式(16)中,灰关联系数α和β的取值对改进熵权法的赋权结果具有很大的影响.以事故5中的直接经济损失指标为例,将传统熵权法与改进熵权法得到的权重差值作为因变量,得到不同关联系数α和β取值下的权重差值如图2所示.
可以看出,相对于关联系数β,权重差值对关联系数α的敏感性更强,且呈负相关性,说明灰靶理论中灰关联差异信息的最小绝对差Δmin对改进熵权法的影响较大.当α∈[0.6,1]且β∈[0.3,0.7]时,改进熵权法与传统熵权法的赋权结果差异趋于平稳,说明改进熵权法的效果较优.

图2 不同关联系数α和β取值下的权重差值Fig.2 Weight deviation under different values of correlation coefficient α and β
5 结论
从模糊数学角度,利用改进熵权-TOPSIS法对铁路事故定级问题做了研究.通过案例对比分析,得到以下结论:
1) 事故定级是事故指标综合评价的结果,通过设计评价指标与不同事故等级间的隶属度函数,利用二者间隶属关系的模糊性,可以综合判断事故的严重程度,有利于量化对比分析.
2) 传统熵权法是根据指标值的变异程度而赋以指标客观权重,该方法虽然具有一定的合理性,但会出现极化指标重要性的现象,为此,可以从指标贡献系数的角度对熵权法进行改进.
3) 通过事故定级结果比对分析,改进熵权-TOPSIS法比传统熵权-TOPSIS 法得出的评价结果更具合理性.改进熵权-TOPSIS法也可用于评价其它多属性决策问题,具有一定的普适性.
在铁路事故定级评价过程中,本文仅选取共性较强且容易量化的指标作为事故的评价依据,因而存在一定的不足,如何更合理地选取评价指标并设计对应的隶属度函数,将是下一步研究的重点.

