风荷组合场景下计及调峰效益的电锅炉和储热系统容量优化配置

于娜，李宏伟，葛延峰，黄大为

（1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林省吉林市 132012；2.国网辽宁省电力有限公司，辽宁省沈阳市 110006）

0 引言

深挖电源侧调峰潜力，全面提升电力系统调节能力，是解决中国东北、华北、西北（三北）地区清洁能源消纳的有效途径之一。针对热电厂的灵活性改造项目得到了国家政策的大力支持[1-3]，东北地区也出台了支持热电厂进行灵活性改造的相关政策，发电企业通过配置储热设备提升热电联产(combined heat and power，CHP)机组的调节能力[4-5]。尽管现有的电力调峰补偿机制对电源侧配置灵活性调峰设备有一定的促进作用，并取得了一定成效，但由于我国的辅助服务市场机制尚不完善，灵活性资源优化配置仍然以管制下的政策性引导为主，有必要从整个电热联合系统的角度出发，对电源侧电储热容量优化配置问题进行深入研究，进而为电热联合系统的运行规划提供必要的技术支持。

针对电储热容量规划的问题，国内外学者已经开展了大量研究工作。文献[6]以供电、供热化石能源消耗总量最小为目标，将规划问题和运行问题相结合，建立电储热容量最优规划模型；文献[7]以规划水平年总运行成本最小为目标，构建了储热系统的最优化规划模型；文献[8]建立了可含热泵的风电供热项目通用数学模型，确定风电供热项目最佳储热容量配置方案；文献[9-10]建立了以全寿命周期成本最小为目标的储热容量优化规划方法。上述文献均将规划问题与运行问题相结合，建立了储热容量最优规划模型；文献[11]则在此基础上，将储热的分布也考虑在内，以经济效益为优化目标，构建了满足一定比例热负荷的电加热器和蓄热装置的最佳容量和分布的数学模型；为响应国家清洁能源消纳行动计划，推进辅助服务补偿（市场）机制建设；文献[12]从整个电热联合系统的角度出发，以综合效益最大化为目标，建立一种储热系统辅助电网调峰的优化配置模型；文献[13-15]给出了配置储热参与调峰市场的基本数学模型。

上述文献从不同角度研究了电储热系统容量优化配置的模型和方法，取得了一定的研究成果。但上述研究较少从系统整体角度考虑调峰效益与系统风电接纳的平衡关系，对于反映可再生能源发电功率等不确定性因素的场景分析问题，仍需进一步深入研究，以期在电锅炉和储热系统容量配置中计及电热联合系统运行中的不确定因素。

为解决上述问题，本文将建立计及调峰效益的电锅炉和储热系统容量配置的双层优化模型，以在实现弃风和运行成本最小的前提下获得最优的调峰效益。

1 基于HMM 的风-荷组合场景构建

考虑到风电功率受风速影响而具有间歇特性和不确定性，为了确保电热综合能源系统运行的安全可靠性，必须在规划和运行阶段考虑风电功率的随机性。目前对于风速不确定性的处理大多认为风速服从Weibull 分布，根据采样数据来近似获得风速序列，然而这种方法忽略了序列的时间尺度，可用于系统的可靠性评估等场景，而不适用于计算系统含时间尺度的指标，如日、年运行成本等[16]。

本文构建的是规划与运行相结合的电热综合能源系统电锅炉与储热优化配置模型，根据典型日风电出力曲线以及负荷需求曲线计算系统年化总成本。所研究的优化问题的输入参数，即风电出力和电/热/需求，由于其昼夜，季节和年度变化而与不确定性相关联。为了处理这些不确定性，应该考虑合理数量的情景，因为一组完整的历史情景会导致计算难以处理[17]。在本文中，采用基于HMM 方法[18-19]模拟风电以及电/热负荷的不确定性矩阵，该矩阵由减少数量的场景组成，其特征与历史场景的随机性程度相似。本文只考虑风电出力以及电热负荷的不确定的组合场景问题，没有考虑调峰市场调峰价格的不确定，我国目前还没有完善的调峰市场，调峰价格受人为和社会因素影响较大，本文采用调峰价格因子 α1和 α2来等效描述调峰价格的不确定。HMM 方法采用矩阵和三次变换分别捕获历史场景中的相关性和随机矩[20]。前4 个随机矩，即期望，标准偏差，偏度和峰度，通常被认为足以保留历史情景的随机特征[18]。该过程描述如下：

1）首先，计算历史小时风电出力和电热负荷需求的目标矩和含风电出力以及电热负荷需求的目标相关矩阵R，并根据式(1)对R 进行归一化处理[18]，其中和分别为第i 列向量的第l个归一化矩和第l 个目标矩。l=1，2，3，4 分别表示期望值，标准偏差，偏度和峰度。

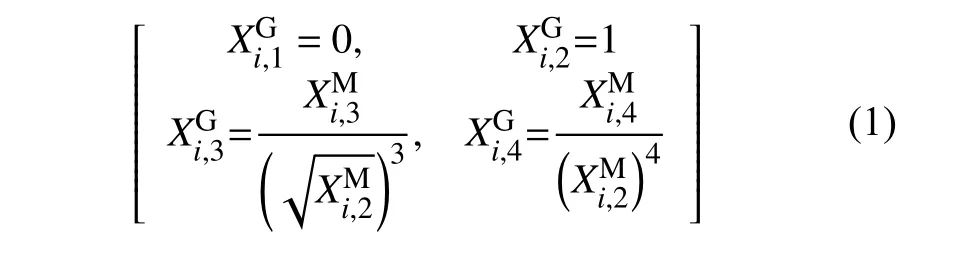
式中：i=1，2，3 分别表示风电出力、电负荷和热负荷。

2）随机生成含Nu个不确定因子的Nh个场景，即风电出力（X1）、电负荷（X2）以及热负荷（X3），以获得随机矩阵 XNu×Nh[18]。

3）根据式(2)进行矩阵变换[18]，将随机矩阵XNu×Nh变换为矩阵 YNu×Nh以满足矩阵R，其中L 是通过Cholesky 分解确定的R 的下三角矩阵。

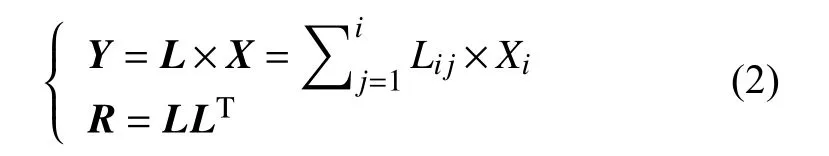
4）根据式(3)进行立方变换[18]，将 YNu×Nh转换为标准化场景矩阵ZNu×Nh以满足。假设目标场景(Xi,l(Zi))等 于，根据公式(4)，可以计算式(3)中的参数d1,i、d2,i、d3,i、d4,i。

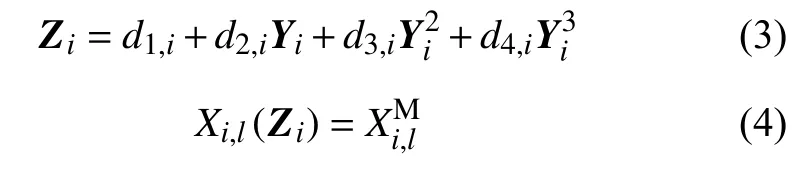
5）当分别在式(5)和式(6)中给出的矩误差( ζm) 和相关误差( ζc)小于预定阈值时，可以得到收敛解，即。其中，式(5)中的是第i 个生成列向量 Zi的 第l 个矩。式(6)中和分别是生成场景和目标场景的相关矩阵。

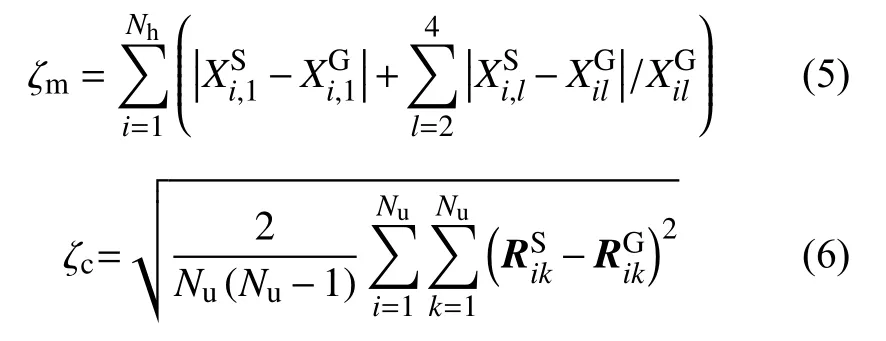
6）最后，将矩阵 ZNu×Nh进行变换以满足，并根据式(7)获得不确定矩阵包含风电出力（），电负荷（）以及热负荷（）场景。

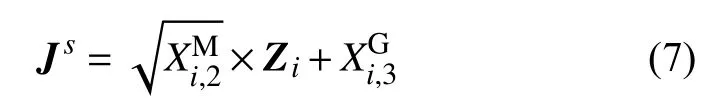
最后得到不确定矩阵 Js，其中包含风电功率场景以及电热负荷需求场景。由 Js矩阵中的元素组成风-荷组合场景集合S。

2 基于双层优化的电锅炉和储热系统容量优化模型

2.1 上层优化模型

根据文献[21]中关于东北地区调峰辅助服务市场的调峰交易规则，建立以所有待规划的热电厂年化调峰净收益最大为目标的上层优化模型。如文献[19]所述，由于Nh个情景的发生概率是一致的，因此使用权重因子(ω =Ny/Nh)将式（9）中给出的运营年度调峰净收入从Nh个情景扩展到Ny=8760 h。

2.1.1 目标函数

上层优化模型的目标函数为：

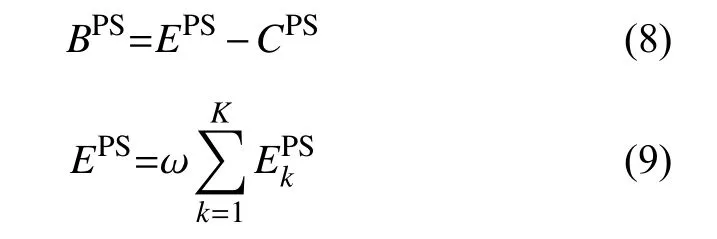
式中： BPS为所有待规划热电厂的年化调峰净收益；EPS为 所有待规划热电厂的年冬季调峰收益；CPS为所有热电厂冬季参与调峰年成本；K 为所有待规划热电厂的数量；为待规划的热电厂k 的年化调峰净收益；表示热电厂k 的年冬季调峰收益；表示热电厂k 冬季参与调峰年成本； ϑk为待规划CHP 机组的集合；T 为供暖季总调度时长；为组合场景S 下t 时段的相应机组的调峰服务结算价格；为调峰功率；表示为热电厂k 配置的电锅炉在t 时刻的耗电功率；表示为CHP 机组最大电出力值；分 别为调峰市场第一档和第二档出清价格上限； α1和 α2分别为调峰价格因子， α1,α2∈(0,1]，分别用于表征调峰市场第一、二档调峰价格的年平均水平。本文假设可以根据历史交易数据对两个档位出清价格的平均水平进行估算，以 α1和 α2两个因子来体现相应档位的出清价格平均水平；表示热电厂k 配置的电锅炉单位容量成本； ρEBM表示热电厂配置的电锅炉单位容量维护成本；表示热电厂k 规划的电锅炉额定功率；表示为热电厂k 规划的储热设备单位容量成本； ρHSM表示为热电厂k 规划的储热设备单位容量维护成本；表示为热电厂k 规划的储热设备的容量。

本文构建的双层优化模型中的上层优化模型以所有待规划的热电厂年化调峰净收益 BPS最大为目标。主要包括调峰收益 EPS和 调峰年成本 CPS两部分。其中热电厂获得的调峰收益的调峰功率主要为将CHP 机组的部分发电功率通过电锅炉转化为热功率进行供热的部分功率再减去运行负荷率为50%以上的CHP 机组需要降至负荷率为50%的CHP 机组出力的部分功率，即式(12)所示。而调峰成本由配置电锅炉的投资和维护成本配置储热系统的投资和维护成本两部分组成。

2.1.2 约束条件

求解上层优化模型需要满足以下约束条件：1）电锅炉额定功率约束为

2）储热设备的容量约束为

2.2 下层优化模型

下层模型以组合场景S 下的有偿调峰条件下的总燃料成本消耗最小和弃风最小为目标，以电力平衡和热力平衡等作为约束条件。

2.2.1 目标函数

下层优化模型的目标函数为：

式中： Cs为 组合场景S 下系统运行总成本；分别为组合场景S 下调度周期内纯凝机组的煤耗成本，CHP 机组的煤耗成本和弃风惩罚费用； NG为纯凝机组的台数； Ps,i,t为组合场景S下纯凝机组i 在t 时段的输出功率； ai、 bi以 及ci为纯凝机组i 的成本系数；和 Hs,i,t分别表示系统组合场景S 下第i 台CHP 机组在t 时段的电功率和热功率； µi0、 µi1、 µi2、 µi3、 µi4和 µi5为CHP机组i 的成本系数； NW为 风电场个数；为组合场景S 下风电场i 在t 时段的发电功率；为组合场景S 下风电场i 在t 时段的计划功率； r为弃风惩罚因子。

2.2.2 约束条件

在组合场景S 下的下层优化模型需要满足以下约束条件：

1）纯凝机组出力约束为

2）纯凝机组的爬坡速率约束为

3）CHP 机组电热出力约束为

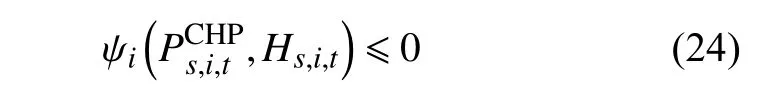
式中： ψi(·)为CHP 机组i 的电功率和热功率工况约束。

4）CHP 机组爬坡速率约束为[22]

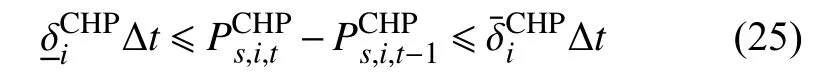
5）风电场运行约束为

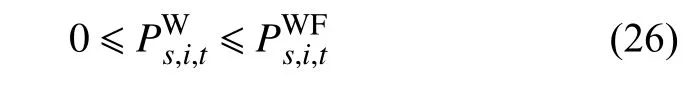
6）电锅炉运行约束为

7）供热平衡约束为

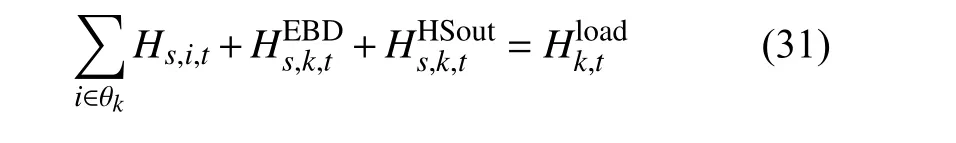
8）电功率平衡约束为

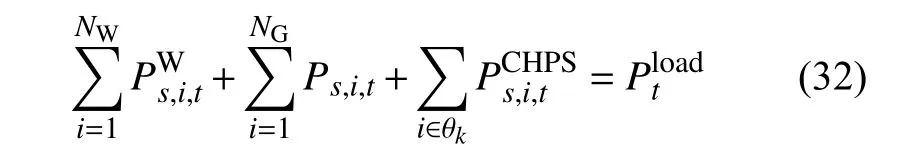
9）储热设备的运行约束为

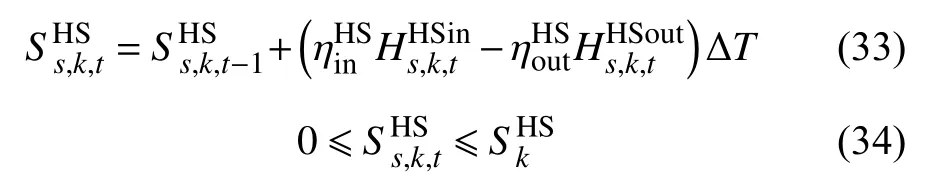
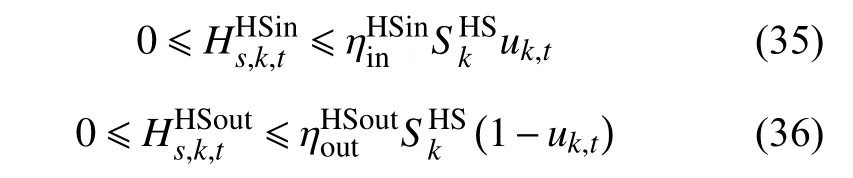
10）储热装置吸放热功率约束为式中： uk,t为0-1 变量。

11）同一时刻储放热约束为

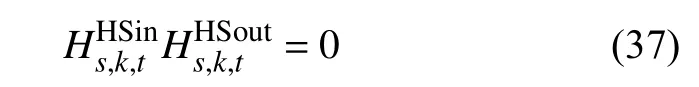
2.3 模型求解

本文针对电锅炉功率和储热系统容量优化配置建立了双层模型属于混合整数非线性双层规划问题，使用非数值优化算法求解难度大、使用CPLEX 单独进行求解耗时长，且难以满足CPLEX的收敛精度要求[23]。为提高收敛性和减少求解耗时，本文采用PSO 与GAMS 软件中CPLEX 求解器相结合的混合策略对本文提出的双层优化配置模型进行求解。

下层优化模型以组合场景S 下的有偿调峰条件下的总燃料成本消耗最小和弃风最小为目标，采用商业优化软件CPLEX12.6 进行优化求解；上层优化模型为以所有待规划的热电厂年化调峰净收益最大为目标，采用粒子群优化算法进行寻优求解。模型求解的流程图见附图A1。

3 算例分析

3.1 算例描述

3.1.1 算例相关参数和数值

本文所构建的算例系统，包含3 个热电厂以及1 个风电场，每个热电厂配置3 台CHP 机组以及一台纯凝机组。仿真实验数据采用的是东北某地区单个风电场2017 年全年风电出力数据，如附录A 附图A2 所示。风电场2017 年最大风电出力为400 MW，供暖季期间最大电/热负荷需求分别为1490 MW 和940 MW，供热面积约1900 万m2。纯凝机组参数如附录A 附表A1 所示。算例的相关参数和数值如附录A 附表A2 所示。

3.1.2 风电功率和电/热负荷的组合场景生成

由于本文采用的仿真实验数据过多，增加了计算上的复杂性，因此本文对选取的仿真实验数据进行场景生成得到典型场景进行仿真计算。根据本文选取的仿真实验数据采用HMM 方法确定历史数据的期望，标准偏差，偏度和峰度，然后生成风电出力以及电/热负荷典型数据；在兼顾计算速度和精度的基础上，根据式(5)的矩误差计算公式计算不同的场景数与目标场景数的随机特征值，附录A 附图A3 给出了不同的场景数与历史场景数的随机特征值（期望，标准偏差，偏度和峰度）的矩误差关系图，可以发现随着场景数的增加，选取的场景与历史场景的矩误差也逐渐减小，当生成的场景数为120 时，其矩误差精度可以满足本文研究的精度要求。选取得到的典型场景如附录A 附图A4、附图A5 和附图A6 所示。根据样本数据进行本节基于上述建立的电锅炉和储热系统的优化配置模型开展仿真分析，通过算例验证前述所建立的双层优化模型的合理性与有效性。

3.2 电锅炉和储热系统优化配置结果

本文针对东北某地区实测电热负荷数据以及风功率预测数据进行分析并对电锅炉和储热系统优化配置模型进行求解。实验所得结果如表1所示。

由表1 的实验结果可知，各个热电厂根据自身情况采用了不同的电锅炉和储热系统配置方案。所建模型中电热系统总共配置了365 MW 的电锅炉和466 MW·h 的储热系统，消纳弃风2091 MW·h，弃风消纳率达到了99.57%，达到了我国东北地区清洁能源消纳行动计划的目标[1]。其中热电厂3配置了最多的电锅炉和储热系统，得到了最高的调峰收益2.9002×106元，以及消纳弃风999 MW·h，占总弃风消纳的47.57%。

表1 电锅炉和储热系统优化配置结果Table 1 Optimal allocation results of electric boilers and heat storage systems

选取2017 年采暖季某日实测数据，基于电锅炉和储热系统的规划结果开展运行分析，以分析风机、纯凝机组、CHP 机组、电锅炉功率以及储热系统的运行状态。统计了相关实验结果如图1和2 所示。本文假设等效电负荷等效热负荷

由图1 的实验结果可知，热电厂配置电锅炉后，在时段2:00～6:00 以及时段18:00～24:00 时提高了低谷负荷水平，为风电提供了更多的上网空间，有效降低了弃风电量；由图2 的实验结果可知，热电厂配置储热系统后，在供热高峰时段，如时段4:00～8:00 以及时段20:00～24:00 时，在满足供热负荷的同时能够有效缓解热电厂CHP 机组供热的供热压力。合理的配置电锅炉和储热系统可以实现电热联合系统的“削热峰”以及“平电谷”。

3.3 配置电锅炉和储热系统后风电消纳情况分析

通过配置电锅炉和储热系统既可以提高热电机组的调节能力，又可以为风电提供足够的上网空间。本节旨在分析地区电网配置电锅炉和储热系统后对地区风电消纳情况的影响。以2017 年采暖季某日实测数据为例分析，结果如图3 所示。

由图3 的实验结果可以看出在配置电锅炉和储热系统后，可以很明显的提高地区电网的风电消纳能力。尤其是在0:00～9:00 以及19:00～24:00两个时间段，风电预测出力较高，在未配置电锅炉和储热系统前造成弃风功率较多，弃风率分别高达27.69%和15.02%。而在配置电锅炉和储热系统后，弃风率分别降到0.38%和0.13%。由此，配置电锅炉和储热系统后可以为风电提供足够的上网空间，促进风电消纳，可以有效的缓解我国东北地区弃风问题。

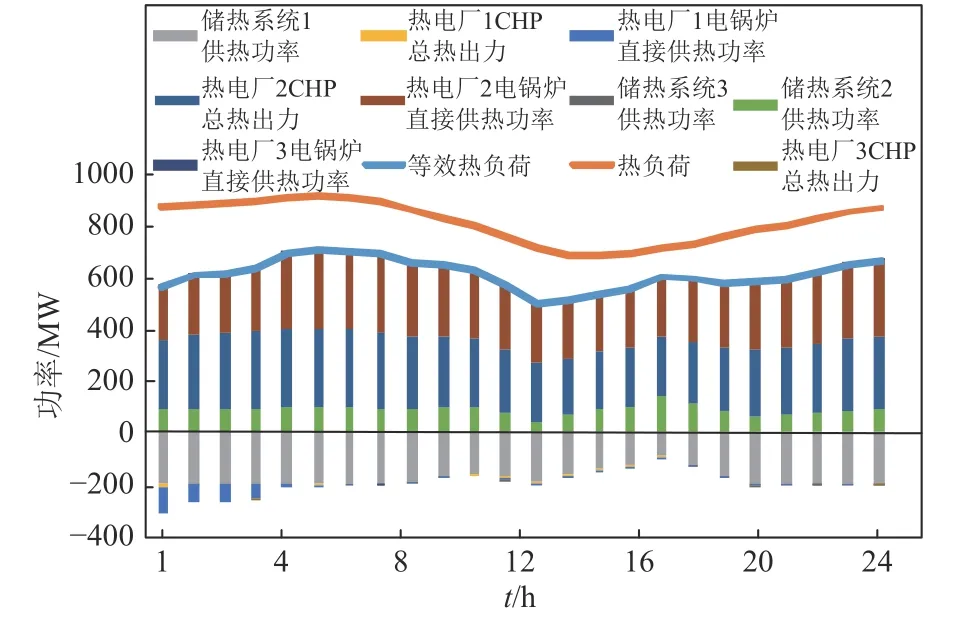
图2 2017 年采暖季某日内的热力系统的运行结果Fig.2 Operation results of thermodynamic system in a certain day during the heating season of 2017

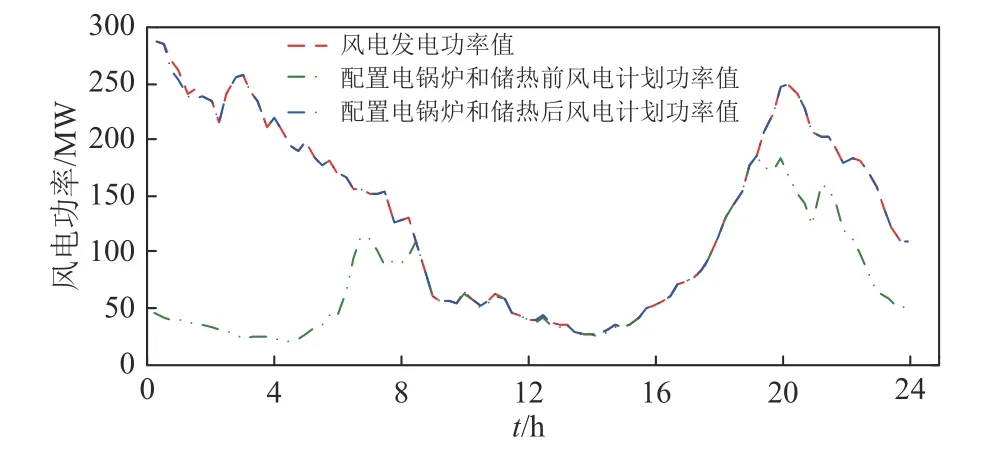
图3 风电发电功率及配置电锅炉和储热系统前后系统风电出力情况Fig.3 Wind power and system absorption of wind power before and after the allocation of electric boilers and heat storage systems

3.4 影响优化配置结果的因素分析

3.4.1 调峰价格

调峰市场的调峰价格对调峰市场的调峰功率交易有着直接影响，也会对热电厂配置的电锅炉和储热系统容量产生影响。本节旨在研究调峰市场调峰价格对于电锅炉和储热系统容量配置的影响，试探讨分析出满足最优的电锅炉和储热系统规划容量要求的价格区间。实验结果如图4 所示，统计了相关实验数据如表2 所示。

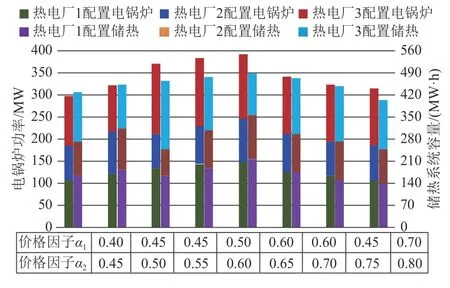
图4 改变调峰价格因子对优化配置结果影响对比Fig.4 Comparisons of the impact of changing peak shaving price factors on optimal allocation results

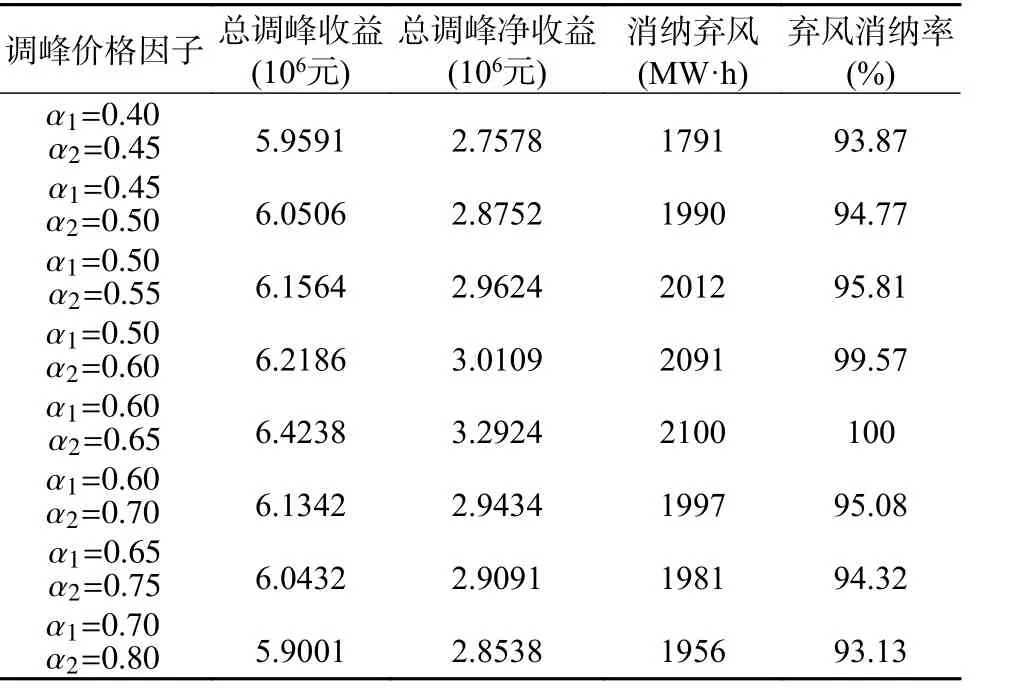
表2 改变调峰价格因子对优化结果的影响对比Table 2 Comparisons of the impact of changing peak shaving price factors on optimization results

根据图4 的实验结果可以看出，调峰辅助服务市场的价格对于电锅炉和储热系统容量的配置确有影响。随着调峰价格因子的增加，所有热电厂配置的电锅炉和储热系统的容量开始呈逐渐增长趋势，当调峰价格因子 α1达 到0.60， α2达到0.65 时热电厂总配置电锅炉和储热容量达到最大值，结合表2 统计的实验结果分析可以发现，此时的弃风消纳率可以达到100%，实现了弃风的完全消纳。随后热电厂配置的电锅炉和容量开始减少，这是由于当调峰市场调峰价格过高时，对于风电场而言，购买调峰资源所需成本可能会高于弃风惩罚所带来的成本，因此会降低对调峰资源的需求，导致热电厂会减少电锅炉和储热系统的配置容量。结合表2 的实验结果可知，当调峰价格因子 α1在 区间[0.50，0.65]， α2在区间[0.55，0.75]时，热电厂配置的电锅炉和储热系统的容量，可以得到较好的调峰收益以及弃风消纳效果。

3.4.2 电锅炉的投资成本

本节旨在分析考虑电锅炉的投资成本对电锅炉和储热的优化配置的影响。在不改变储热系统投资成本的前提下，通过改变电锅炉的投资成本，分析其对电锅炉和储热系统的优化配置影响。图5 给出了电锅炉成本变化下的电锅炉和储热系统的配置结果，其中CR1、CR2、CR3分别表示热电厂1、2、3 配置电锅炉的单位成本。统计相关实验数据如表3 所示。

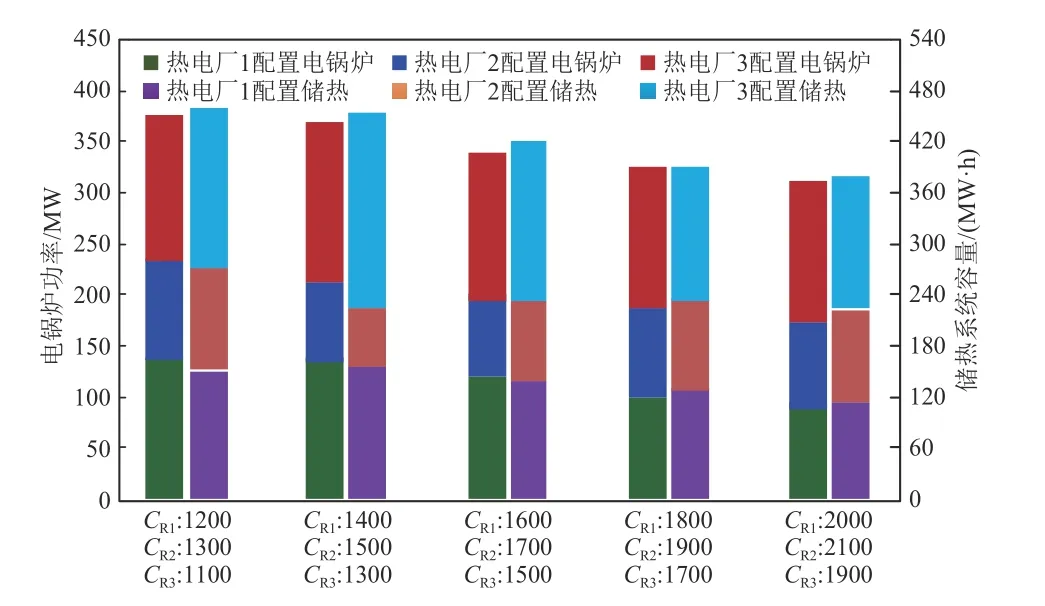
图5 改变电锅炉投资成本对优化配置结果影响对比Fig.5 Comparisons of the impact of changing the investment costs for electric boilers on optimal allocation results

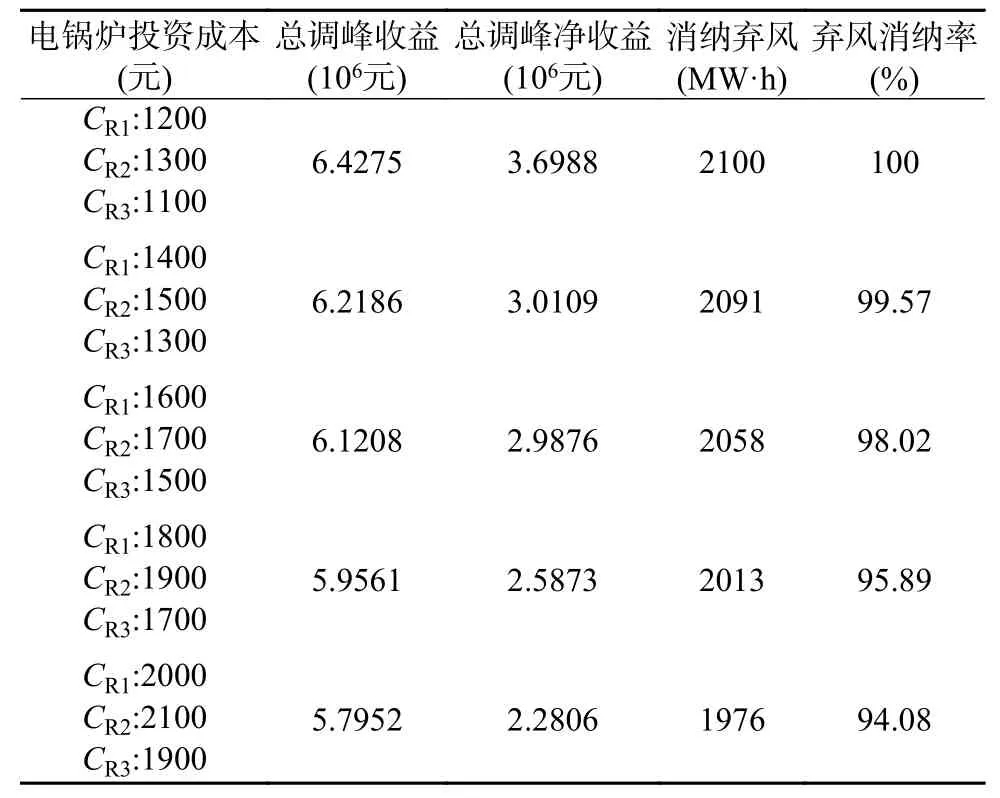
表3 改变电锅炉投资成本对优化结果的影响对比Table 3 Comparison of the influence of changing the investment costs of electric boilers on optimization results

由图5 的结果可以很明显的发现，电锅炉的投资成本的改变，影响了电锅炉和储热系统的配置方案。随着电锅炉投资成本的增加，电锅炉的规划功率在减少，储热系统的规划容量也有降低。这是由于电锅炉的规划功率降低将直接影响储热系统的储热容量的减少，在改变电锅炉投资成本时，会间接影响储热系统的配置方案。根据图5的实验结果，从规划的结果可以看出，虽然随着投资成本的增加，热电厂总体配置电锅炉和储热的容量有所降低，但是从单个热电厂角度出发，热电厂3 配置电锅炉的技术较为成熟，投资成本是三个热电厂中最少的，且热电厂的CHP 机组的装机容量也较高，煤耗成本低，使得热电厂3 配置的电锅炉在热电厂总规划容量的占比是最高的，可以提供更多的调峰资源以获得更多的收益。结合表3 的统计数据可知，合理的投资成本可以提高调峰收益以及改善风电弃风情况。

3.4.3 储热系统的投资成本

储热系统的投资成本也是影响电锅炉和储热的优化配置结果的关键因素。图6 给出了储热系统投资成本变化下的电锅炉和储热系统的配置结果，其中CH1、CH2、CH3分别表示热电厂1、2、3 配置储热系统的单位成本。统计相关实验数据如表4 所示。

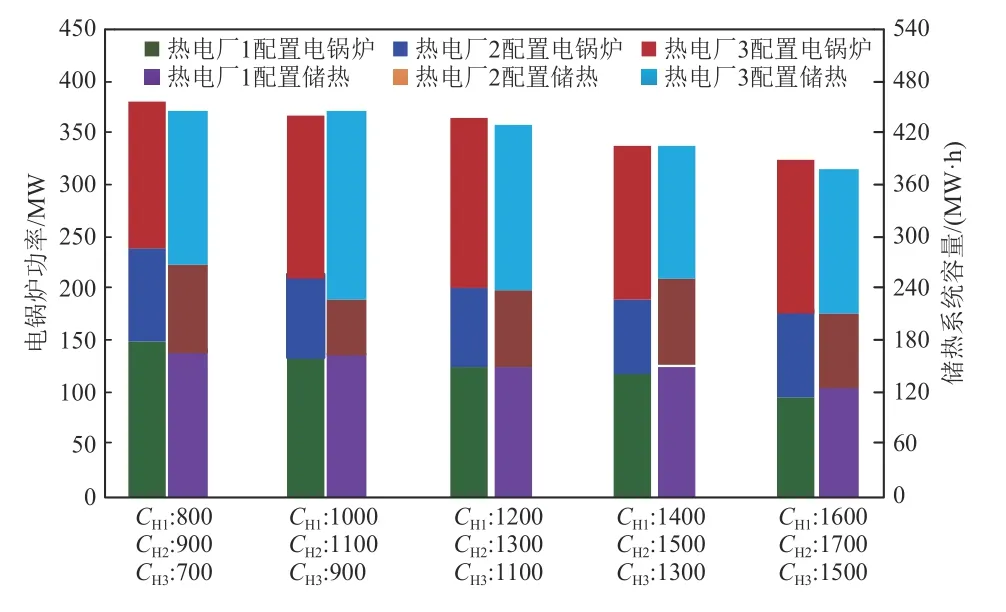
图6 改变储热系统投资成本对优化配置结果影响对比Fig.6 Comparison of the influence of changing the investment costs for thermal storage system on the optimal allocation results

由图6 的结果可以发现，储热系统投资成本的改变，影响了储热系统的配置方案。结合表4的实验结果可以看出，随着储热系统的投资成本的增加，储热系统的规划容量在减少，而对电锅炉的影响较小，且调峰收益逐渐降低，风电消纳功率也有下降。这是由于储热系统的容量对于电锅炉的规划功率没有直接影响，所以在改变储热系统投资成本时对储热系统容量改变不大，对于电锅炉规划方案影响较小。

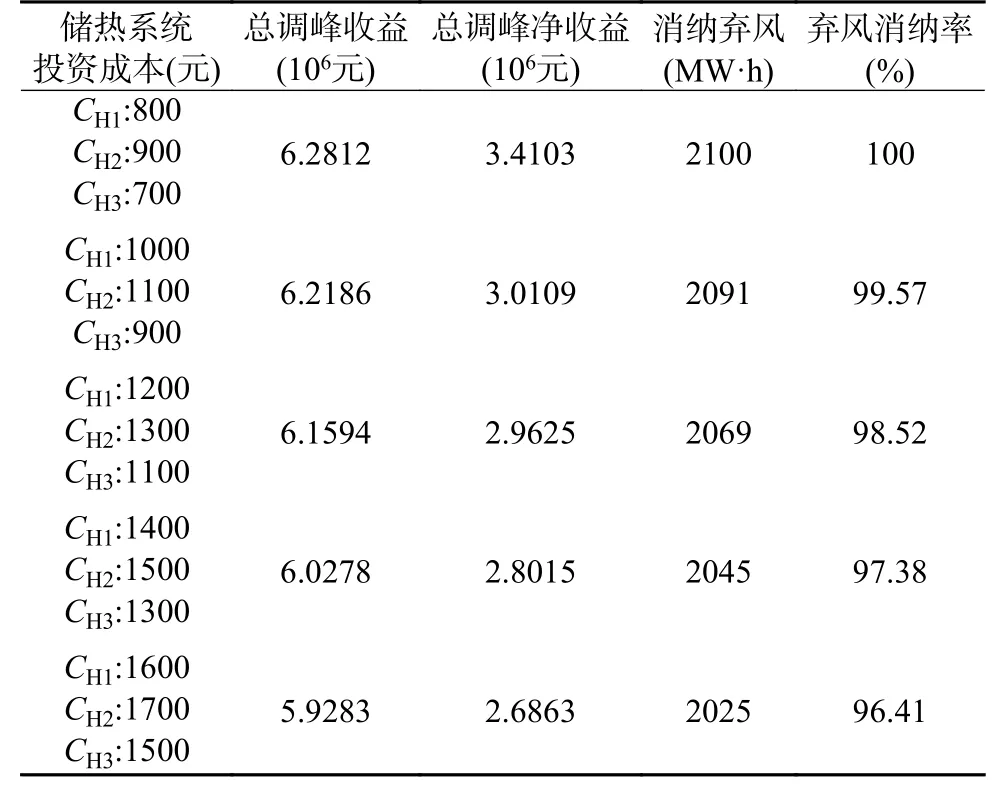
表4 改变储热系统投资成本对优化结果的影响对比Table 4 Comparison of the effects of changing the investment costs for thermal storage system on optimization results

4 结论

1）以调峰收益最大为目标对电锅炉和储热系统进行优化配置，促进了风电资源消纳，有效地缓解东北地区弃风问题。

2）通过调峰市场出清价格的改变可以直接影响电锅炉和储热系统的配置结果。合理的制定调峰价格可以得到较好的电锅炉和储热系统配置结果，且可以提高整体的社会效益以及改善弃风消纳效果。

3）电锅炉和储热系统的投资成本的改变均会对电锅炉和储热系统的优化配置方案造成影响。其中改变电锅炉的投资成本对其配置方案影响较大。

随着中国电力市场规则和调峰运行激励政策的不断完善，考虑基于网络约束的各热电厂主体的具体情况，通过不同的电锅炉和储热设备配置方案，共同参与电力调峰辅助服务市场获得收益，将是本文后续的研究内容。

附录A

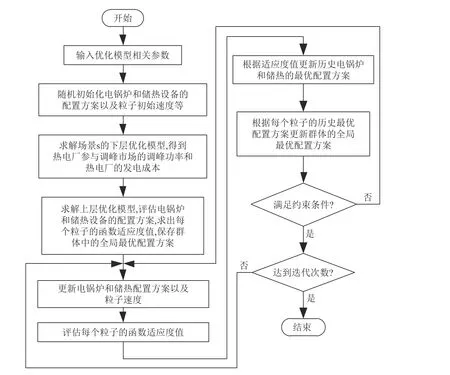
附图A1 模型求解流程图Fig.A1 Flow diagram of solving equation

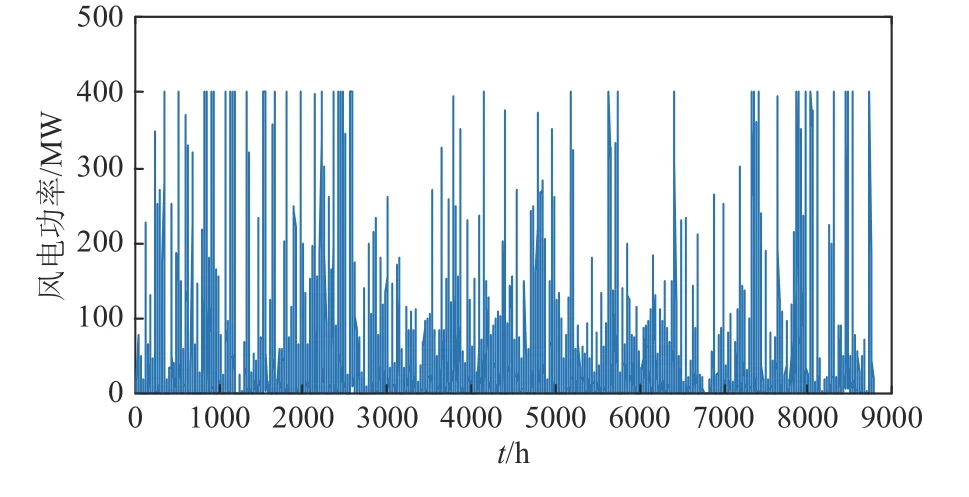
附图A2 东北某地区2017 年全年风电功率Fig.A2 Wind power in a northeast area in 2017

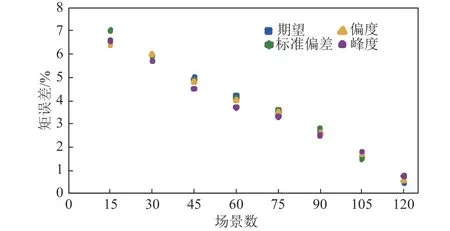
附图A3 生成场景和目标场景之间的矩误差百分比Fig.A3 Percentage of moment errors between generated scenarios and target scenarios

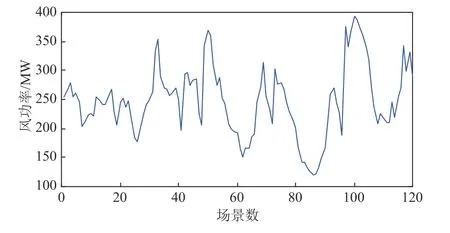
附图A4 风功率场景Fig.A4 The scenarios of wind power

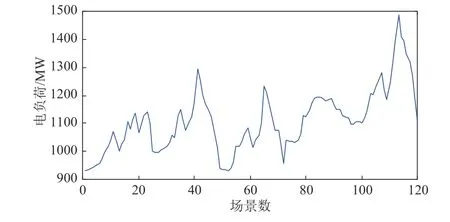
附图A5 电负荷场景Fig.A5 The scenarios of electric load

附图A6 热负荷场景Fig.A6 The scenarios of thermal load

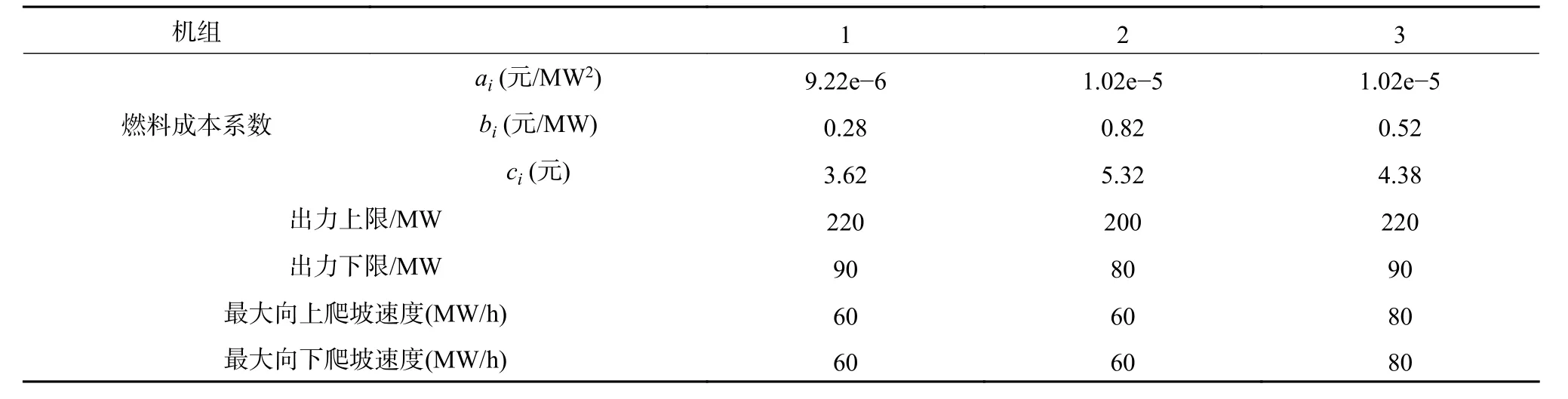
附表 A1 纯凝机组参数Table A1 Conventional unit parameters

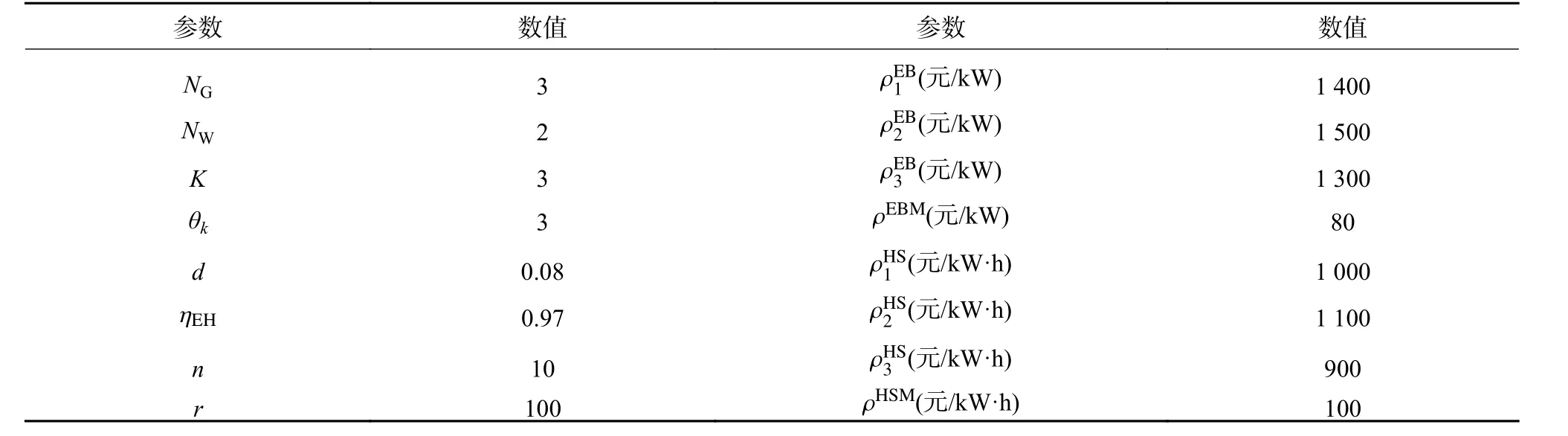
附表 A2 算例的相关参数和数值Table A2 Parameters and values in calculation example

（本刊附录请见网络版，印刷版略）