基于委托-代理理论的负荷率可选择电价最优合约设计

黄海涛，杨洋，况夫良，贺敏

（1.上海电力大学，上海杨浦区 200090；2.国网甘肃省电力公司，甘肃省兰州市 730030）

0 引言

电价机制改革是电力体制改革的重要内容。2015 年新一轮电改方案强调要放开售电侧。本轮改革的主要目的之一是赋予工商业电力用户自主选择不同种类电价的权利。用户作为电能的消费者，将不再只是价格的被动接受者，而是能够根据自身用电方式与要求来自愿选择不同类型的电能消费和支付方式[1]。它能够以一种友好、互动、自愿、平等的方式，提高供电服务质量，保障用户权益，实现社会福利的帕累托优化。

可选择电价这种看似简单的菜单式电价制度，实则包涵着深刻的经济激励机制理论[2]。在菜单式的套餐选项合同中如何通过设计恰当的激励来解决逆向选择问题是其技术难点与关键所在[3]。然而，目前可选择电价研究成果多为概念与体系架构、国外实践及我国政策实施建议[1-5]。定价理论与机制的研究正在摸索中，文献[4-5]分别构建了最优多部制和负荷率分档的电价模型，提出了等效的可选择两部制电价；上述方法缺乏可选择性的理论证明，为此文献[6]采用泰勒展开式进行数学证明，并给出了相应的可选择性条件；文献[7]则针对两部制峰谷电价，提出了一种基于用户选择预判的可选择套餐实用化模型。以上研究均是首先根据经验等提出一种可选择电价套餐，然后再证明它满足可选择性条件。这种研究方法只适用一个特定问题的研究，对于可选择电价研究不具通用性。此外，它也难以回答该电价套餐是不是最优价格、是否存在更优的价格机制等问题。因此，亟需应用经济学激励机制理论突破可选择电价的关键技术，提升其研究方法的科学范式。

因此，针对政府电力零售负荷率可选择定价制度的逆向选择问题，应用经济激励机制设计理论，分析定价部门和用户之间的委托-代理关系，并建立了相应的模型，给出了该问题的严格数学解析解。结果表明，在该方案下定价部门所让渡的信息租金为零，即本文所设计的负荷率可选择电价机制为最优机制，可以实现定价的公平性并解决菜单式套餐合约中的逆向选择问题。最后，算例验证了其有效性和科学性。

1 激励机制与委托-代理理论

1.1 委托-代理理论

对政策销售电价可选择合约制定中定价部门和用户的博弈关系进行分析，不难发现该博弈可以视为一种交易关系且在信息不对称的情况下进行，而这可用经济学中的委托-代理关系深入分析。在信息经济学中，委托-代理问题指任何一种涉及不对称信息的交易，通常将交易过程中拥有私人信息的一方称为代理人，另一方则称为委托人。在委托-代理关系中，出于自利行为，代理人选择行为时首先考虑的是如何使自己的收益最大化，一般不会真正自觉地关心委托人的收益问题。因此，委托-代理问题主要研究委托人如何根据现有的信息，在“理性人”的假设条件下，设计一个可行的机制以实现其期望效用最大化，从而达到双方共赢的最佳效果。

在自利行为的驱使下，各类交易市场中合约的选择情况可能与设计者的预期出现偏差，这也称为“隐藏知识（信息）”。由此便产生了选择性价格中的逆向选择问题。即代理人会凭借信息优势选择对于自身最有利的行动（“说假话”），这可能会导致委托人利益受损。而信息经济学中的激励,即委托人针对代理人的行动,目的是使代理人从自身效用最大化出发,自愿选择与委托人目标相一致的行动。因此，需针对逆向选择问题，设计相应的最优激励机制。

1.2 激励机制

经济激励机制设计所讨论的问题是，对于一个既定目标，在自由选择、自愿交换、信息不完全等分散化决策条件下，设计出一个经济激励机制，使得参与者的个人利益和设计者的既定目标一致。本文便是在上述条件下，对选择性电价中定价部门的配置效率（定价目标）和信息租金抽取上的权衡取舍进行讨论分析，并设计出最优激励机制。此处信息租金是指用户拥有比定价部门更多信息而获得的额外收益，它是为了让用户选择既定选项而让渡给用户的经济激励。

因此，需要设计一个最优激励机制，尽可能减免信息租金，从而解决“隐藏信息”带来的逆向选择问题。即应针对逆向选择问题设计相应的委托-代理激励机制模型。在委托-代理理论中，合约一般是在事中（代理人知道自身类型委托人不知）阶段签订[8]，本文亦在此基础上进行建模与求解。

2 负荷率可选择电价合约设计的基本框架

负荷率可选择电价合约的预期实现过程为：定价部门预先制定多种电价合约供用户自愿选择，用户根据自身负荷率及其他因素（考虑自利行为等）进行套餐合约的选择，拥有充分的选择权。不难看出，负荷率可选择电价合约设计过程在信息不对称情况下进行，该委托-代理问题涉及定价部门与电力用户2 类参与人。定价部门设计并提出交易合约，即在交易过程中拥有一定垄断权力，在委托-代理模型中为委托人；用户在交易中明确自己的负荷率类型而定价部门不知（即用户拥有私人信息），为代理人。

为解决负荷率可选择价格中的逆向选择问题，关键是要寻求一种激励机制。本文运用经济学激励机制设计理论，设计了负荷率可选择电价最优合约：首先确定定价目标（此次定价目标为成本回收和公平定价的基础上再为用户提供多种价格的选择权以保障更好的供电服务品质）；然后开展用户供电成本分析；在此基础上，根据经济学委托-代理理论[9]，针对负荷率可选择电价中的逆向选择问题，建立相应委托-代理模型；最后通过数学推演求解得到最优解（即最优合约），完成最优机制的设计。基本设计框架如图1 所示。

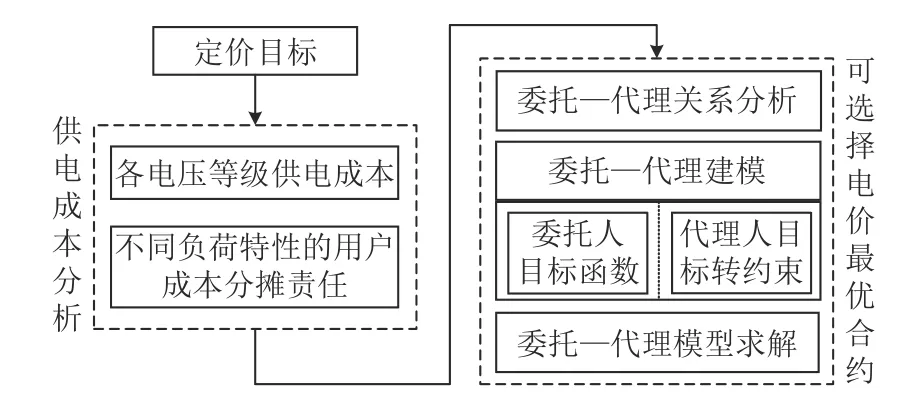
图1 负荷率可选择电价合约设计基本框架Fig.1 Basic framework for design of electricity price contract with selectable load rate

3 数学建模

3.1 考虑负荷特性的用户供电成本及其分摊

公平性和成本回收是我国定价部门制定销售电价的主要原则和目标，它以用户供电成本分析为基础。用户供电成本取决于用户的用电负荷特性，受电电压等级和负荷率是其主要决定因素，本文讨论不同电压等级情况。

3.1.1 各电压等级供电成本分析

供电成本主要包括发电成本、输配电成本和售电成本。售电成本所占比重很小，此处不做讨论。根据文献[10]，按分电压等级输配电成本，计算电压等级y 单位电量的平均供电成本 ACy：

其中，

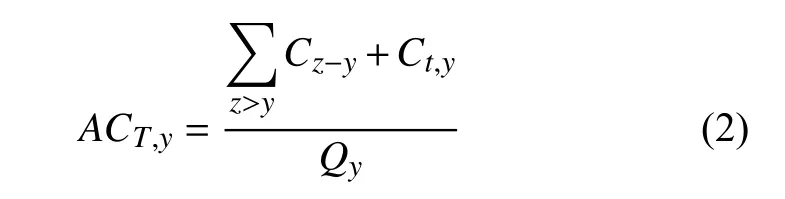
式中： ACT,y和 ACG分别为电压等级y 用户的平均输配电成本和单位电量平均发电成本； Cz−y为电压等级y 用户应分担的高电压等级z 的输配电成本，由高电压等级z 的输配电成本和电压等级y以上各电压等级逐级下送电量比例之乘积来确定；Ct,y为 电压等级y 的平均输配电容量成本； Qy为电压等级y 的用电量。

3.1.2 考虑负荷特性的用户供电成本分摊

引入负荷率作为消费者类型参数，记为θ，用以表征用户的用电负荷特性。则负荷率为 θ的用户通过两部制价格应分摊的供电成本简要说明详见附录1，计算式为：

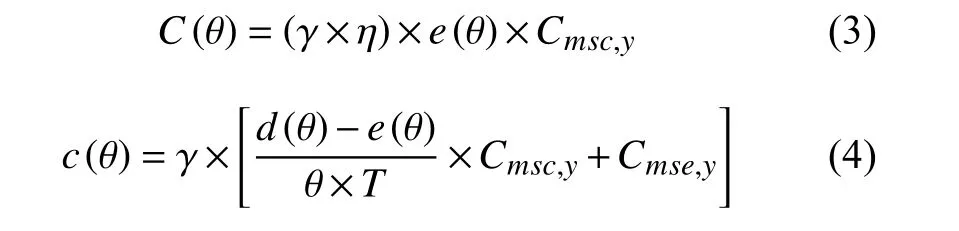
式中：C (θ)和 c (θ)分别为容量成本和电量成本部分，单位为元/月·kW、元/kWh，它反映了负荷率为θ的用户应分摊的供电成本（或者说真实的供电成本）； γ为财务平衡调整系数， η为财务平衡调整系数 γ的折算因子 η =1/(θT)；e 为容量成本由两部制电价中基本电价部分回收的分摊系数；T 为月小时数，一般取720。 Cmsc,y和 Cmse,y为电压等级y的系统边际容量成本和边际电量成本，为常数。

3.2 委托-代理数学模型

考虑到选择性电价中的逆向选择问题，在电价机制最优合约制定过程中，应满足参与约束和选择性约束。而此处我们默认只存在一家电力公司，因此无需考虑参与约束，需要考虑的约束条件即选择性约束，文中指用户选择与自身负荷率类型相符的套餐选项。这亦可从信息租金上进行解释，定价部门为了让用户真实选择而让渡的经济激励，等价于用户选择与自身负荷率不相符的套餐时所获的额外收益，显然我们希望信息租金尽可能减免。也就是说，用户选择与自身负荷率类型相符的套餐选项时预期收益高于选择与其他选项。选择性条件具体表示为：

将上式移项合并，整理可得：

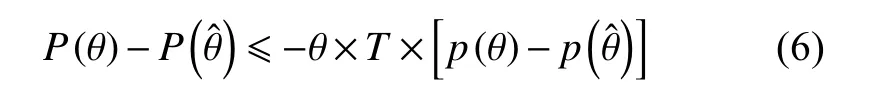
因 P(θ) 、 p(θ)中 θ 均 为连续变量，并假设的极限均存在，将不等式(6)两边同时除以且两端求极值，得到：

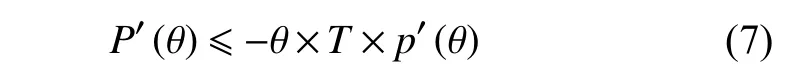
式(7)中负荷率 θ与月小时数T 均为正数，电度电价函数 p(θ)的导函数为负，将其移项后得到约束条件化简结果式(8)：

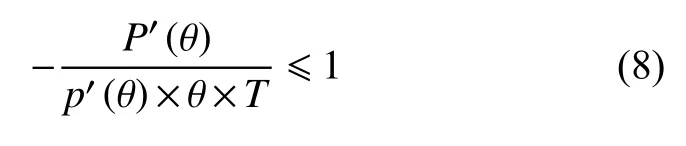
负荷率可选择电价机制设计的相应委托-代理关系见前文第2 节。考虑到本文政府定价部门定价目标为成本回收和公平定价的基础上再为用户提供多种价格的选择权，对任一类型 ∀θ ∈(0,1)用户，建立对应的委托-代理模型为下式(9)、(10)，从而求得的解对于所有类型用户的加总也为最优；对用户而言，其目标已通过选择性约束条件进行相应的转换。具体模型如下所示：

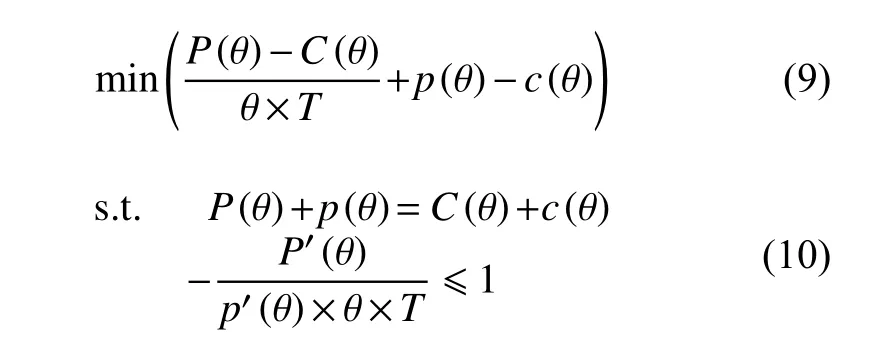
4 委托-代理模型求解

首先将成本函数C (θ)、 c (θ)进行化简以便于求解：

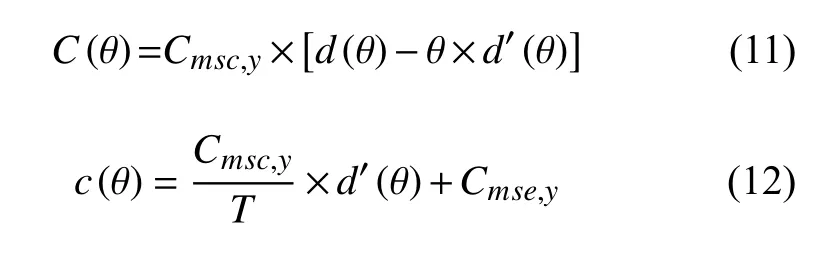
其中，

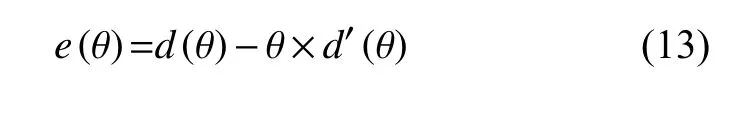
对于含有不等式约束的最优化问题，可以转化为在满足KKT 约束条件下应用拉格朗日乘子法求解。将成本函数代入委托-代理模型中并建立对应的拉格朗日函数进行严格的数学推演求解：

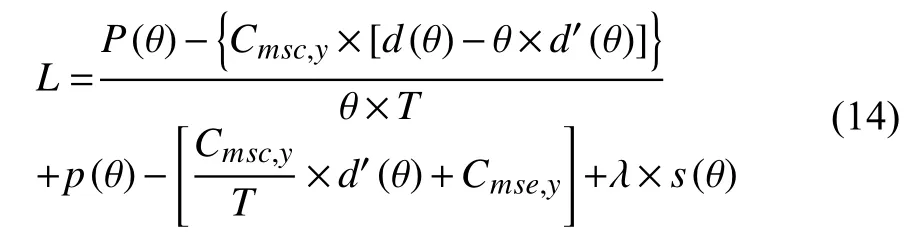
其中，

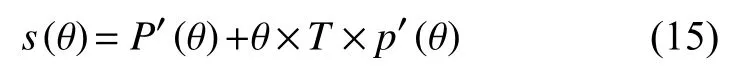
式中： λ为拉格朗日乘子。

该拉格朗日函数对应的KKT 条件如下：

对 λ分情况进行讨论：

1）当 λ =0时，该优化问题即转化为无约束优化问题，考虑到成本补偿，解即为：

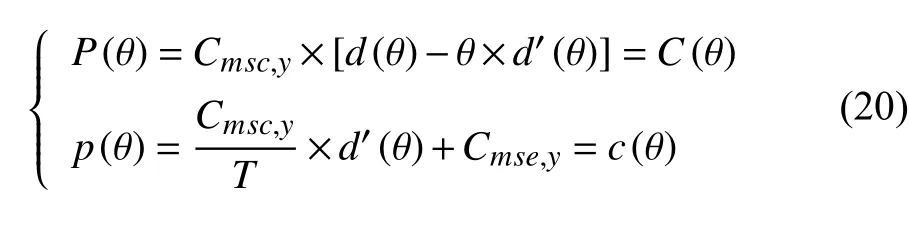
2）当 λ ≠0时，根据KKT 条件中式(19)可知λ ＞0， 随即通过式(17)可知 s(θ)=0，且验证满足式(18)， ∴s′(θ)=0 （ 假 设 P(θ) 、 p(θ)二 阶 导 均 存在）。将KKT 条件化简可得：

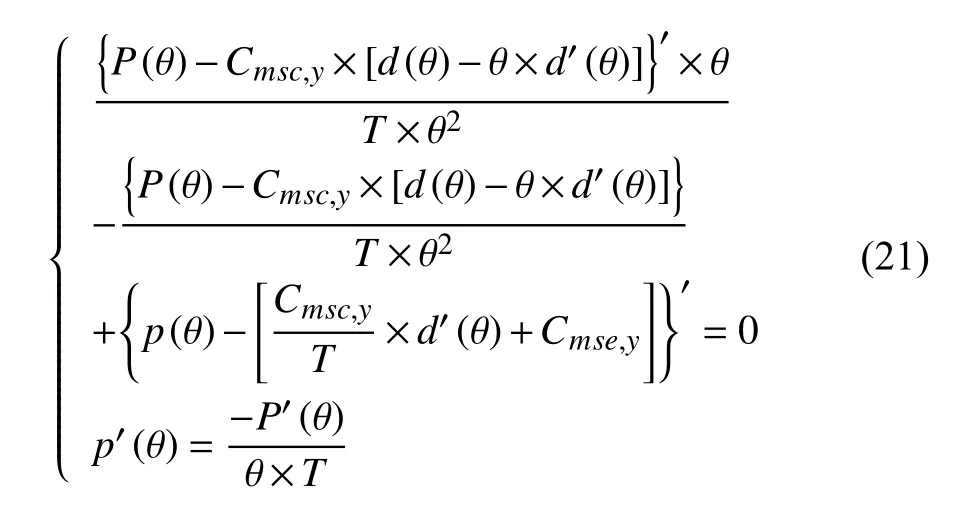
将上式进一步消元化简可得：

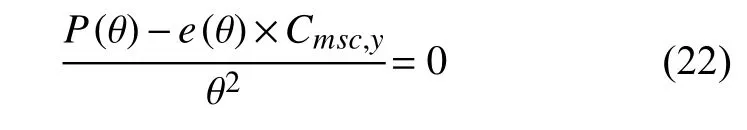
因用户负荷率为正数，上述等式分子部分为零，因此可得到基本电价部分：

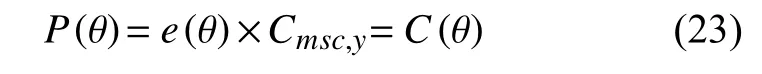
将其代入式(21)可得：

式中：k 为常数。考虑到成本补偿约束P(θ)+p(θ)=C(θ)+c(θ)， 因此k=0， p(θ)=c(θ)。

最终可得到负荷率选择性两部制电价最优定价函数，即最优机制为式(25)：

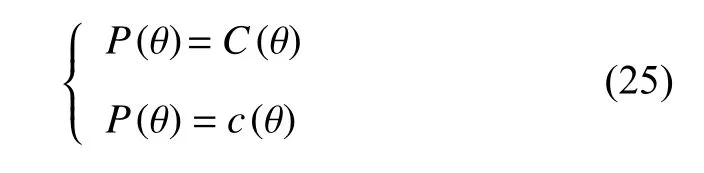
结果表明，在该定价方案下，政府定价部门可以达到既定的定价目标，即在成本回收的前提下实现定价的公平合理性。此外，根据3.2 节可知，信息租金等价为用户选择与自身负荷特性不符的套餐时所获的额外收益，而在该定价合约下，若用户选择其他选项反而需支付更多电费，这种选择显然不符合“理性人”假设。即可说明在该定价合约下，定价部门无需支付信息租金，用户也会自觉选择相应负荷率特性的套餐。所设计的负荷率可选择两部制电价合约为最优价格机制，可以解决菜单式套餐合约中的逆向选择问题。

5 算例

5.1 算例描述与基础数据

本文以某省不同电压等级用户为研究对象，设计负荷率可选择电价。算例以样本用户的用电负荷特性数据为基础，结合用户供电成本数据，制定完全非线性的负荷率两部制可选择电价；最后提出实用化的两部制电价选项套餐，并讨论套餐选项数目对定价效果的影响。

该省抽取的有效样本用户数目为4000 户，其中220 kV、110 kV、35 kV、10 kV 和不满1 kV样本用户分别为450 户、600 户、800 户、1000户和1150 户，用户负荷特性数据见附录二。各电压等级财务平衡调整前后的供电成本基本数据如表1 所示，财务平衡调整系数γ 为1.12。

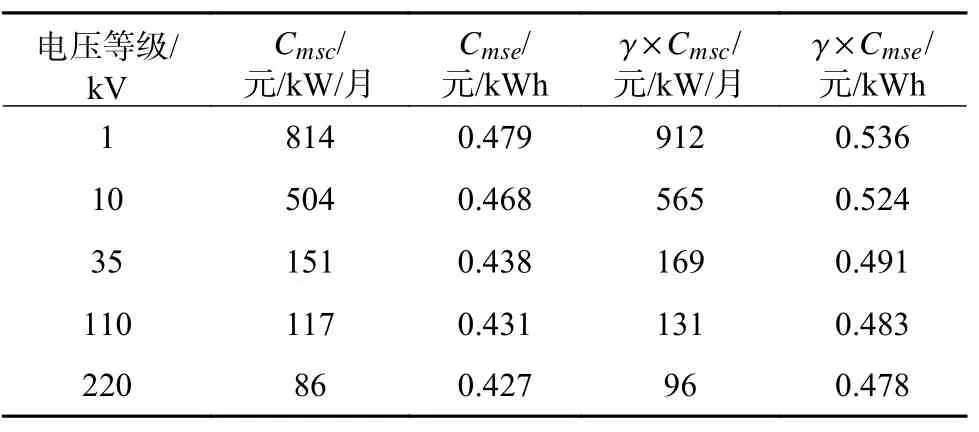
表1 各电压等级财务平衡调整前后的供电成本基本数据Table 1 Basic data of power supply costs before and after financial balance adjustment for different voltage grades

5.2 用户负荷特性分析及供电成本分析

用户的用电负荷特性分析和供电成本分析是可选择电价设计的基础。因各电压等级用户的负荷率—同时率曲线较为近似，此处以35 kV 为例。根据样本用户负荷特性数据，经统计和曲线拟合得到图2 所示的35 kV 用户负荷率—同时率曲线，它是一个二阶可微的单调递增凸函数。

根据3.1.2 节式(3)—(4)，计算得到不同负荷率用户应分摊的供电成本，它是负荷率 θ的函数。容量成本和电量成本部分，单位为元/kW/月、元/kWh，分别为：

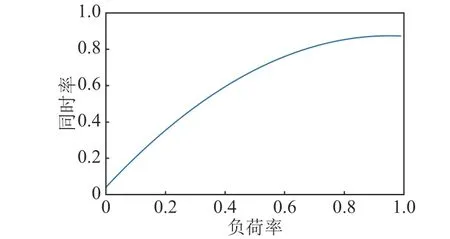
图2 35 kV 用户的负荷率—同时率曲线Fig.2 Load rate-simultaneous rate curve for 35 kV users

5.3 委托-代理模型求解

检验本文提出的负荷率可选择最优合约设计结论式(25)的正确性。以供电成本函数式(26)和(27)为基础数据，应用式(9)、(10)构建负荷率可选择电价的委托-代理模型:

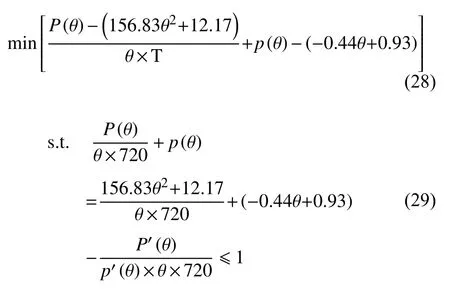
建立对应的拉格朗日函数式(30):

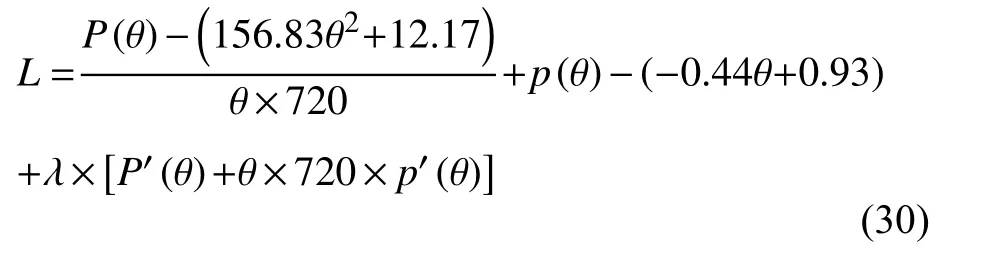
根据KKT 条件对该不等式优化问题进行求解，最终可得最优解（最优价格机制）为：

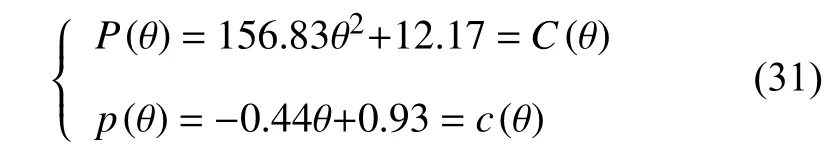
该结果表明，负荷率可选择销售电价最优合约设计即为各选项两部制电价等于不同负荷率用户对应的供电成本。这与前文式(25)一致，验证了本文负荷率可选择电价最优合约设计结论的正确性。在该定价机制下，即“理性人”用户的选择将与定价部门的预期相一致。此外，定价部门无需支付信息租金即可达到定价目标，换句话说无需担心给予用户选择权而造成的定价效益损失，此时用户的信息优势不起作用。同时，该定价机制能合理反映用户供电成本差异，体现定价的公平性，为最优机制。

5.4 负荷率两部制电价可选择套餐

考虑到完全非线性价格形式较为复杂、难以理解，实际中不易操作，故根据负荷率分布情况，对每一电压等级进行负荷率分档并制定负荷率两部制电价的实用化选项套餐，套餐共有3 至4 种两部制电价选项供用户自愿选择，预期负荷率分档如表2 所示。每一电压等级负荷率可选择电价套餐计算结果详见表3。

表2 各电压等级负荷率分档结果Table 2 Load rate grading results of various voltage grades

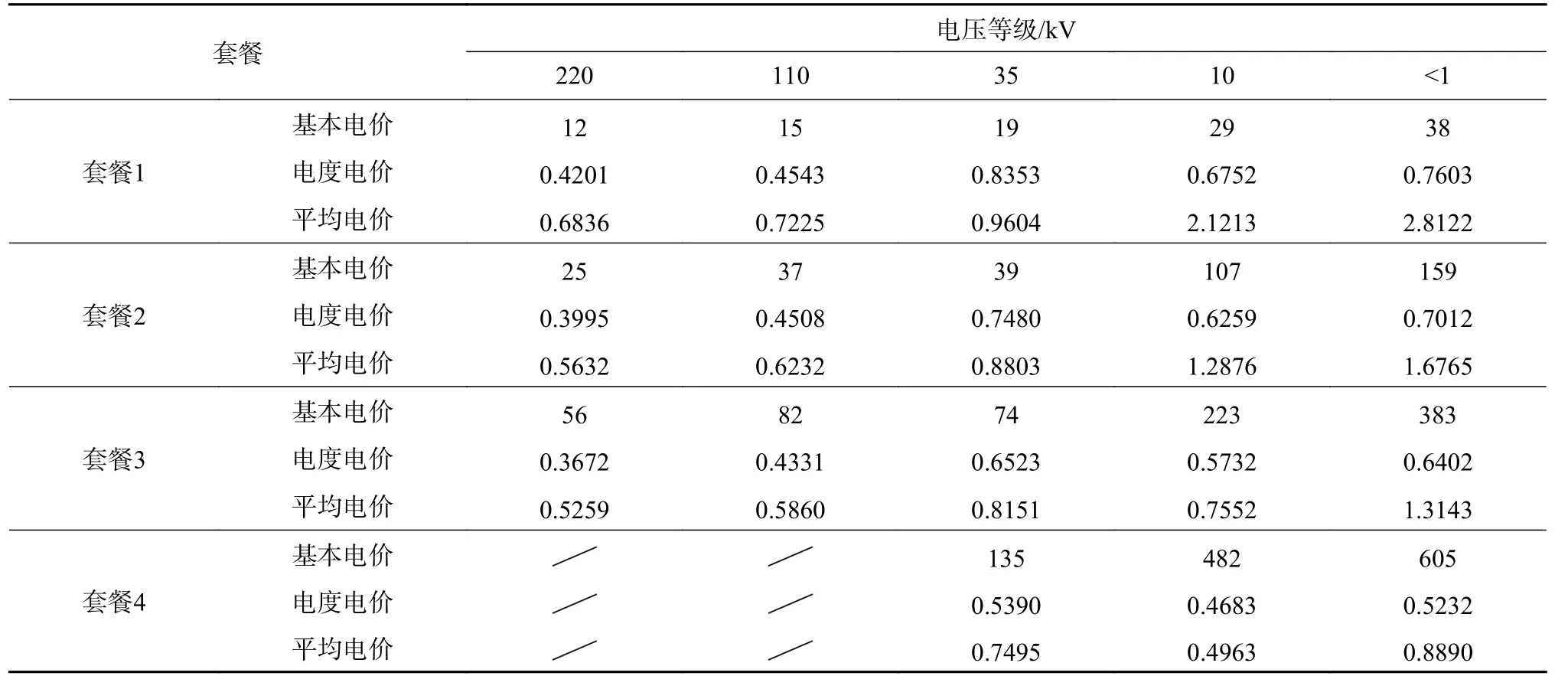
表3 不同电压等级的负荷率可选择电价套餐计算结果Table 3 Calculated results of electricity price packages with selectable load rates for various voltage grades

各负荷率用户选择不同套餐选项时的平均电价如图3 所示，以其中35 kV 电压等级为例进行分析，该图表明：1）用户选择套餐4 时该用户所需支付的平均电价随负荷率的变化关系为紫色曲线，当负荷率大于0.72 时该曲线处于其他3 个套餐选项的平均电价曲线的下方，这表明用户选择套餐4 时的平均电价低于其他3 个选项的情况；因此，定价部门制定了表2 和表3 所示的电价套餐供用户自愿选择这4 个套餐的任意1 个时，当负荷率大于0.72 时，用户会按支付的电价最低情况选择套餐4。2）同理，当负荷率在[0.48−0.72]、[0.3−0.48]、[0−0.3]之间时，用户选择套餐3、套餐2 和套餐1 的平均电价最低。其他电压等级分析与此类似。

前面分析已知信息租金是定价部门为使用户选择自身负荷率相应合约所让渡给用户的经济激励，是用户由于具有信息优势而取得的额外收益。算例分析可得，不同电压等级不同负荷率用户按各自收益最大化选择的结果与定价部门预期选项一致。这表明委托人收益最大化与代理人各自收益最大化相一致，该选择性价格达到了最优定价效果，激励用户说“真话”的信息租金为零。

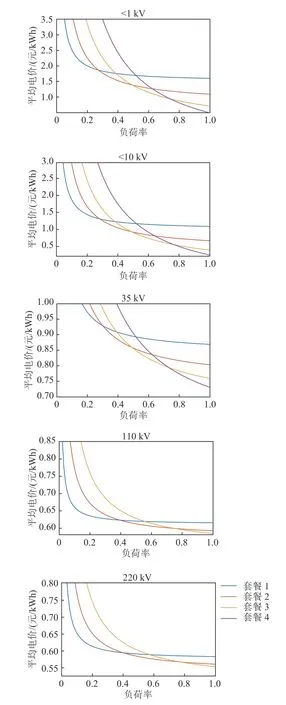
图3 各负荷率用户选择不同套餐选项时的平均电价Fig.3 Average electricity price of consumers adopting different load rate with different package options selected

此外，计算可得图4 不同电压等级完全非线性两部制电价比较图。由图4 分析可得，随着电压等级降低，平均电价升高；同一电压等级下，平均电价随负荷率升高而下降。这科学反映了不同电压等级、负荷率供电成本的差异，体现了定价的公平性。另一方面，负荷率越高平均电价越低，故它能有效引导用户合理用电以提高负荷率；众多用户负荷率提高效益相聚合，有益于减少系统最大负荷，从而降低电网和电源扩容容量和投资。

图4 不同电压等级完全非线性两部制电价Fig.4 Complete nonlinear two-part electricity prices under different voltage grades

5.5 套餐选项数目的讨论

制定可选择套餐时选取不同选项数目，比较计算各个电价套餐与完全非线性价格形式的定价效果，以35 kV 为例，结果如表4 所示，表中“定价效果损失”评估指标用个体用户可选择电价套餐预期选项价格偏离非线性定价价格的绝对值对全体用户的积分，再以总电费支出性标幺化来表征。该结果表明：随着套餐数目的增加，与完全非线性价格的定价效果的差距逐步缩小，当套餐选项数目达3 时其定价效率损失在10%以内，当选项数目达4−5 时其与完全非线性价格的定价效率损失在5%以下，在选择性电价的实践中具有可行性。故在负荷率两部制选择性电价套餐的实用化设计时，选项数目达到4−6 项即可。

表4 不同选项数目的电价套餐与完全非线性电价的定价效率比较Table 4 Pricing efficiency comparison of electricity price package with different option numbers and complete nonlinear electricity price

6 结论

1）本文应用委托-代理理论，建立了相应的负荷率可选择电价的委托-代理的数学模型；通过严格数学推演方法，得到可选择电价合约的优化解，以及相应电价机制设计的制度安排。该分析框架也可以应用于其他可选择电价的研究。

2）完全非线性价格形式的负荷率可选择电价最优合约的选项价格设计应当为不同负荷率用户对应的供电成本；也就是说，该“选项”的两部制价格取负荷率电价水平。该定价机制解决了逆向选择问题，存在使用户说“真话”的负荷率可选择电价的激励机制安排，且信息租金为零。

3）考虑到该可选择电价机制之制度安排在实际政府销售电价制定工作的实用性，在算例设计中讨论了可选择电价选项套餐及选项设计数目问题。结果表明选项套餐形式的负荷率可选择电价，也能够甄别不同负荷率类型的用户，使得不同负荷率用户自愿选择结果与定价部门预期一致，实现公平定价、引导用户合理用电的定价目标；选项数目一般取4−6 个，通常它可以接近与完全非线性负荷率可选择电价相似的定价效果。

本文应用委托-代理理论，对负荷率可选择两部制电价进行了研究，然电价管理实践中更为普遍的是峰谷电价及其与两部制的混合电价，其研究具有更广泛的应用。在数学建模与求解中引入了一些假设条件，如用户知道自身负荷率信息，参与者完全理性等，后续研究可进行改进。

附录A：供电成本分摊简要说明

将电压等级y 供电成本按负荷率和同时率特性分摊给居民用户。由于电力系统生产特性，系统供电成本是所有用户的共同成本，故通常按边际成本将之分摊至各类用户。用户边际供电成本是指系统为满足该用户新增单位用电而增加的成本，它包括长期边际容量成本和边际电量成本。结合我国电力市场和电价政策现状，根据文献[6]，负荷率为 θθ 的 用户边际容量成本 Cmc,y和边际电量成本Cme,y分别为：

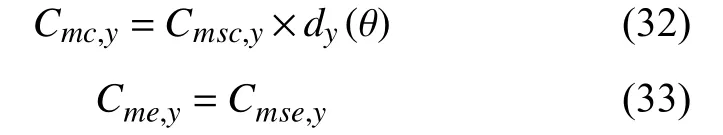
式中：Cmse,y和 Cmsc,y分别为电压等级y 的系统边际电量成本和系统边际容量成本，由系统供电成本分析得到； dy(θ)为 该电压等级负荷率为 θ的用户的同时率。

电力系统供电成本由固定成本和变动成本构成，由于二者成因不同应当通过两部制电价回收。理论上，固定成本应按边际容量成本分摊至各类用户，并通过基本电价回收；变动成本应按边际电量成本分摊至各类用户，并通过电度电价回收。但考虑到科学引导用户合理用电，改善系统峰谷负荷特性，固定成本部分通过基本电价回收，剩余部分通过电度电价回收。则负荷率为 θ的用户通过两部制价格应分摊的供电成本为：

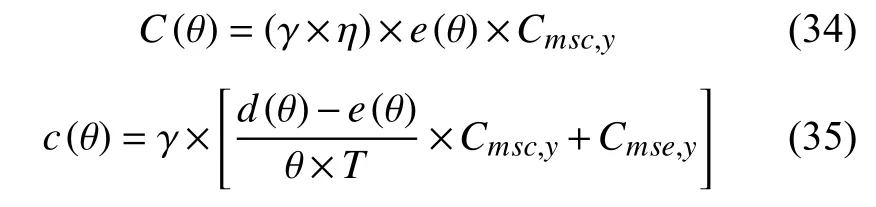
式中：C (θ)和 c (θ)分别为容量成本和电量成本部分，单位为元/月·kW、元/kWh，它反映了负荷率为θ的用户应分摊的供电成本（或者说真实的供电成本）； γ为财务平衡调整系数， η为财务平衡调整系数 γ的折算因子 η =1/(θT)；e 为容量成本由两部制电价中基本电价部分回收的分摊系数；T 为月小时数，一般取720。

附录B：用户负荷特性数据

本文算例部分抽取有效样本用户数目为4000 户，其中220 kV、110 kV、35 kV、10 kV 和不满1 kV 样本用户分别为450 户、600 户、800 户、1000 户和1150 户。考虑到数据完全展示篇幅较大，现通过附表A1 至附表A5 呈现各电压等级部分用户负荷特性数据。

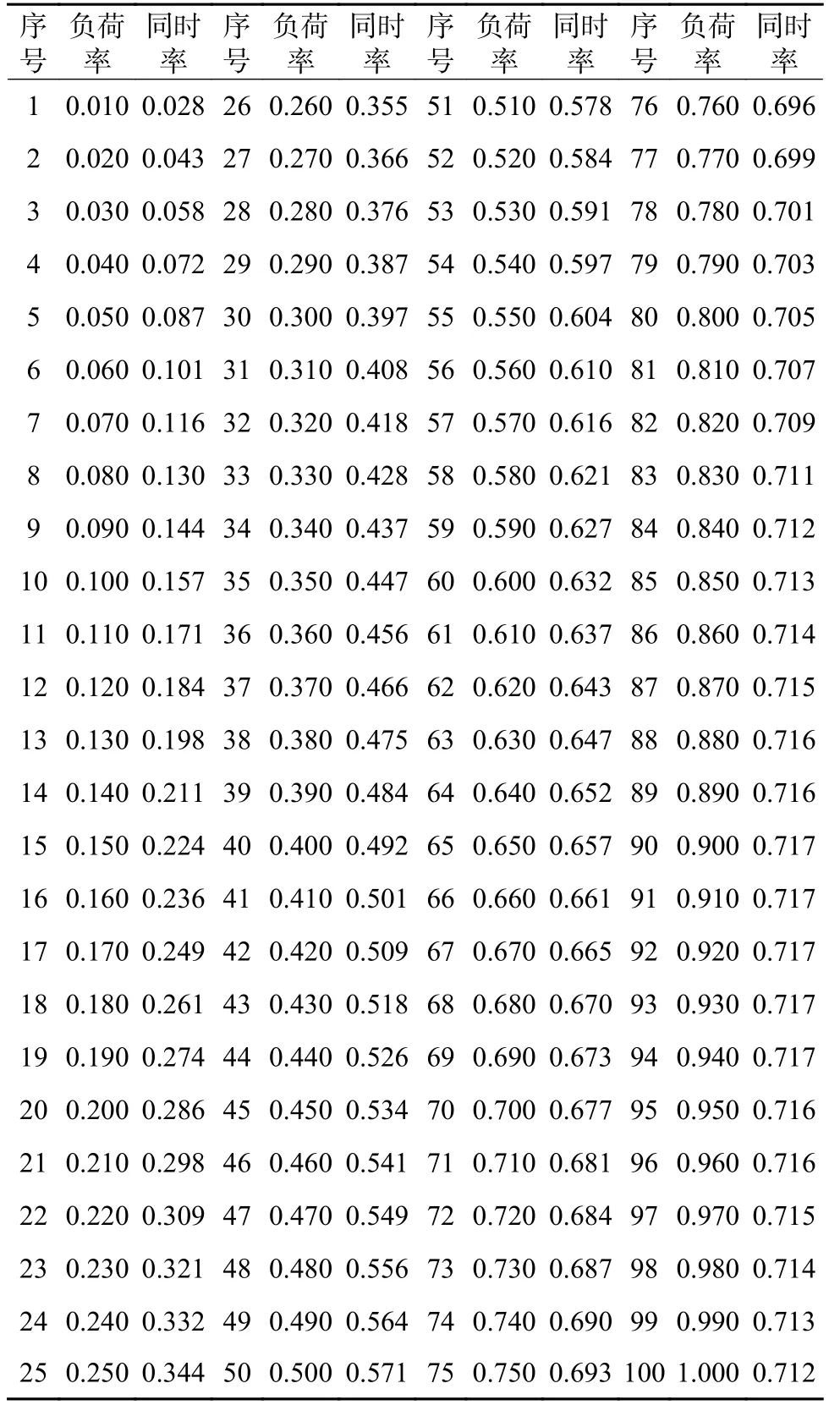
附表 A1 220 kV 用户负荷率—同时率部分数据

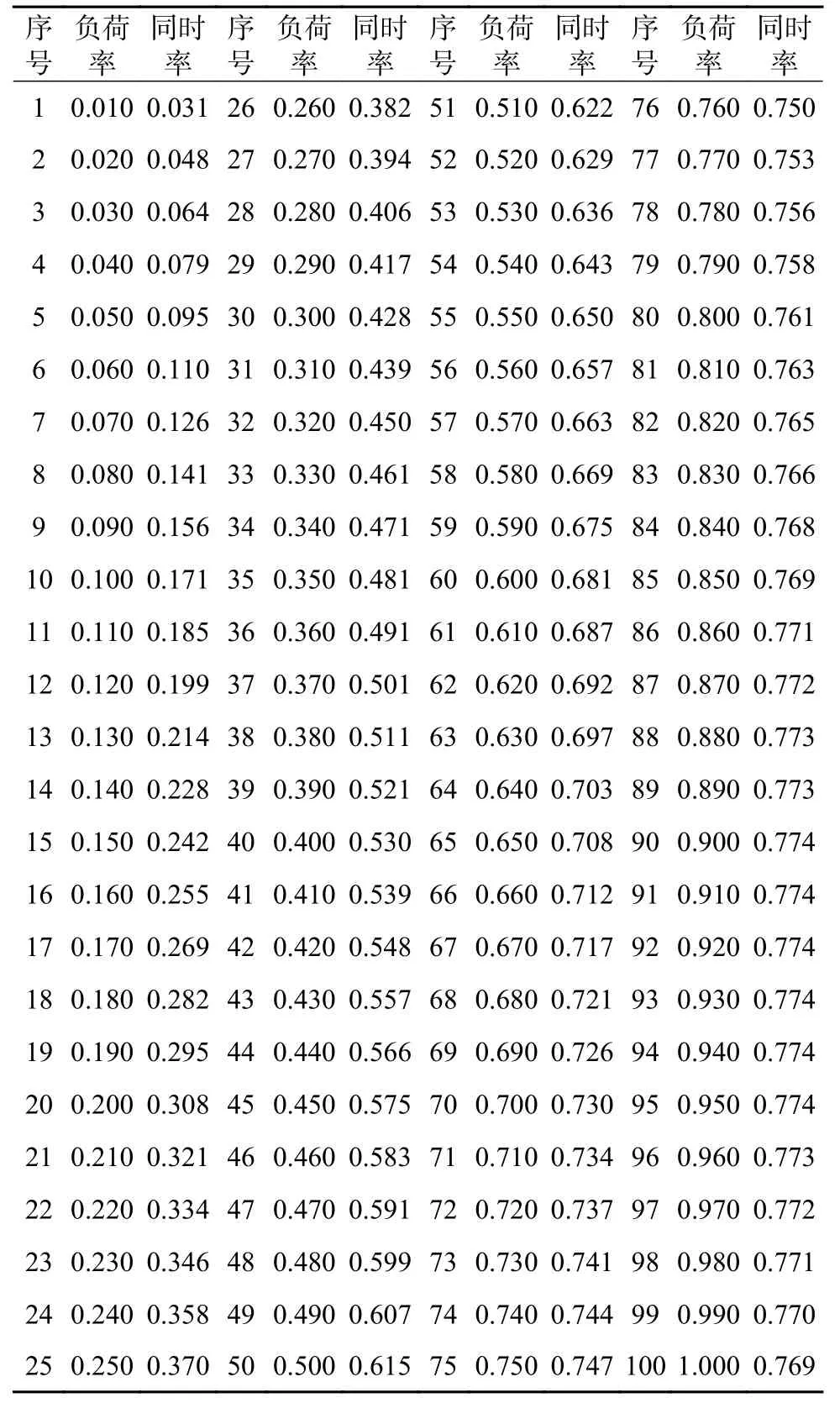
附表 A2 110 kV 用户负荷率—同时率部分数据

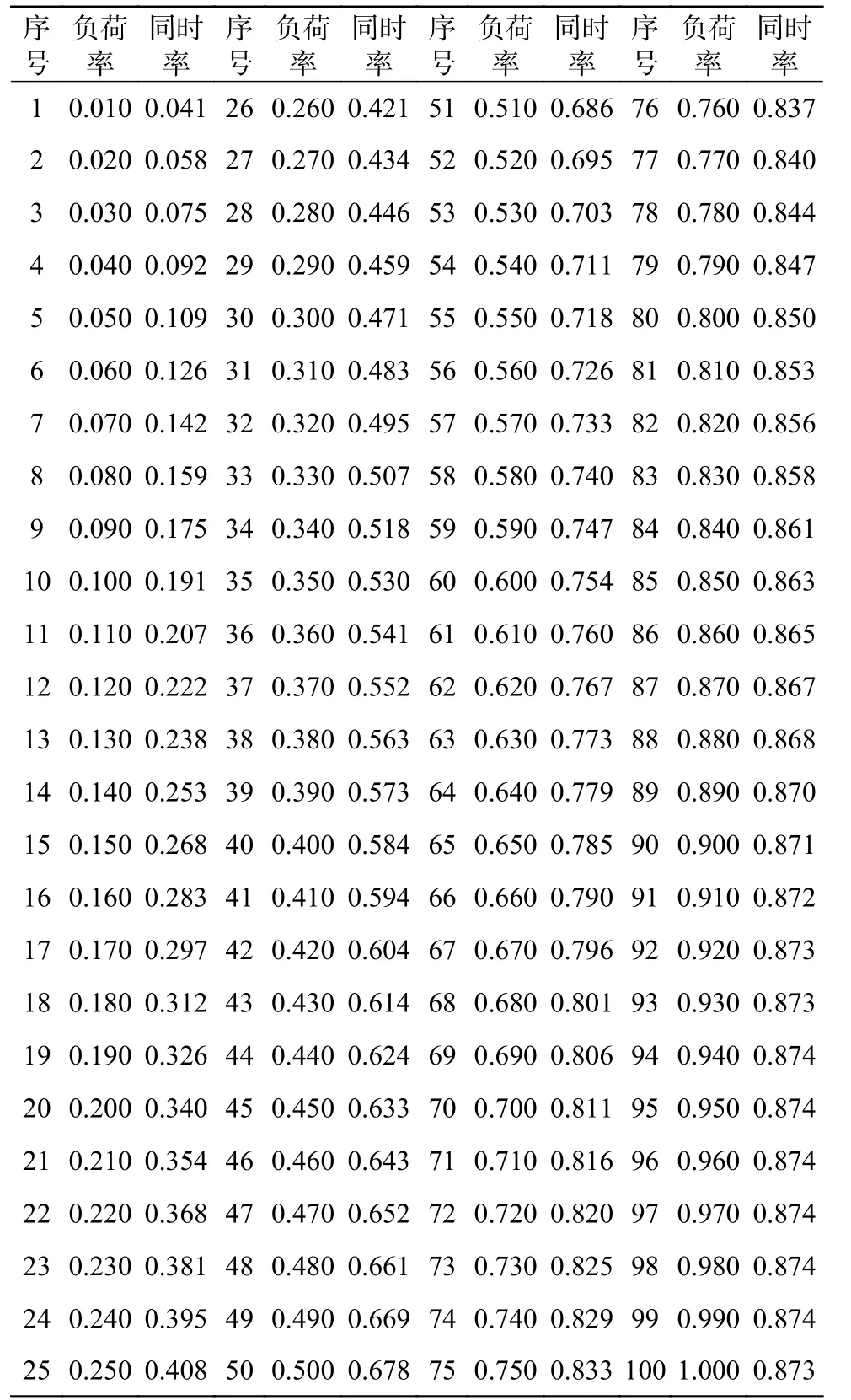
附表 A3 35 KV 用户负荷率—同时率部分数据

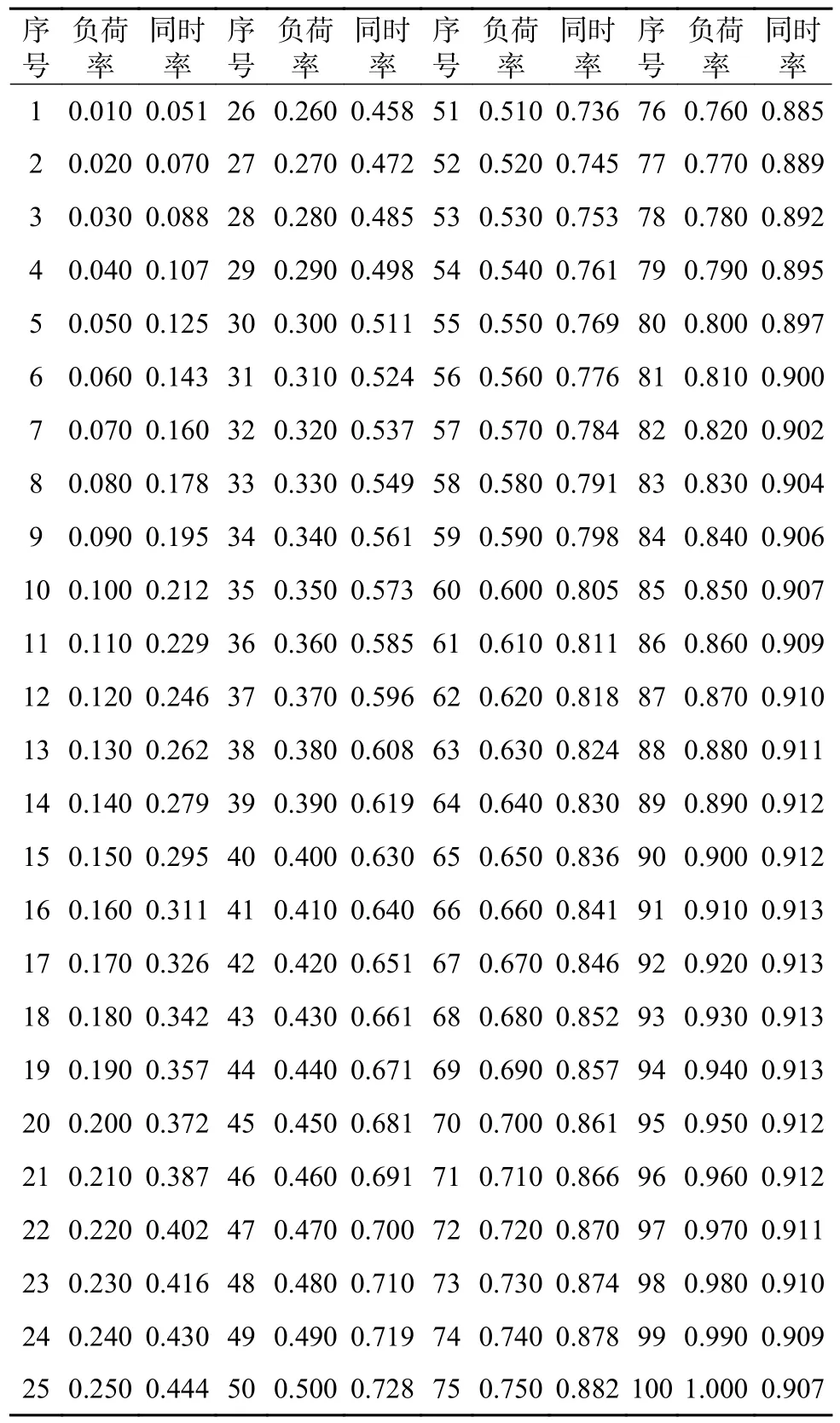
附表 A4 10 kV 用户负荷率—同时率部分数据

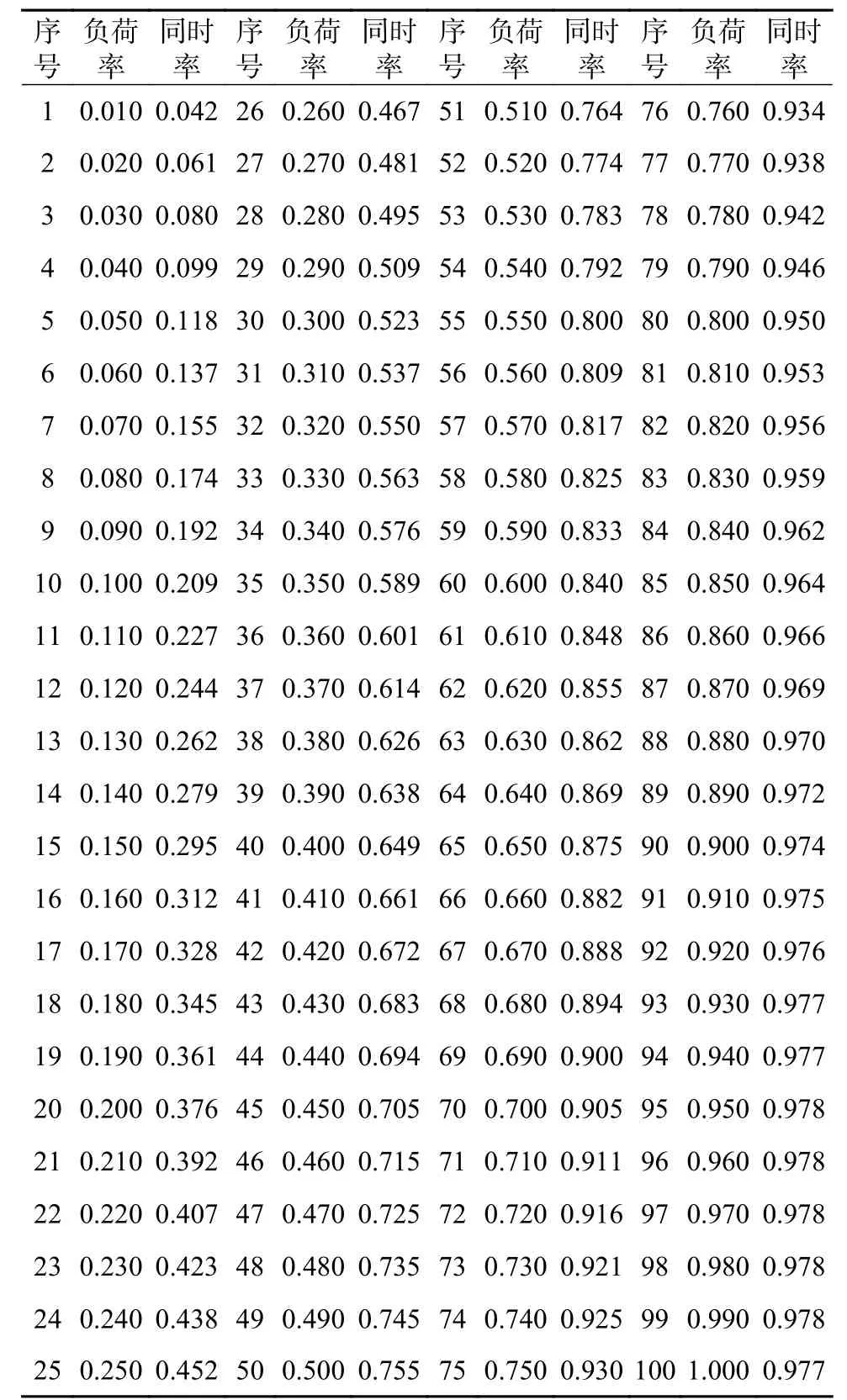
附表 A5 不满1 kV 用户负荷率—同时率部分数据

（本刊附录请见网络版，印刷版略）