断梗激励下葡萄果粒的振动脱落特性与试验

闫 德，汪建晓，罗陆锋，刘文涛，韦慧玲，王金海，刘宝立，卢清华

断梗激励下葡萄果粒的振动脱落特性与试验

闫 德，汪建晓，罗陆锋※，刘文涛，韦慧玲，王金海，刘宝立，卢清华

（佛山科学技术学院机电工程与自动化学院，佛山 528000）

针对夹剪式鲜食葡萄采摘中的断梗振动激励引起的果粒脱落问题，对断梗激励下鲜食葡萄的振动脱落特性与动态响应进行研究。首先建立葡萄果实-分梗动力学模型，推导果实脱落的理论角速度，分析果实-果梗摆动脱落的临界分离条件。然后利用ABAQUS软件分析单颗粒葡萄在断梗激振下的动态响应与摆动趋势，探索在无挤压状态下果实形变过程，从而预测串型葡萄在断梗激励下的实际振动响应。最后对串型葡萄的简化模型进行振动有限元分析，获得葡萄果实在脱落前瞬间相对于果梗结合处的位移、速度、加速度和应力应变等数据，从而确定葡萄的临界振动脱落参数组合。通过仿真试验和采摘振动试验验证模型的准确性。结果表明：在断梗激励下，葡萄果实出现不确定的各向异性扭转摆动；对整串葡萄进行0～25 Hz的扫频分析可知受振果实的临界脱落频率约为4 Hz；受振果实摆动幅度为49.88 mm，速度峰值0.92 mm/s，加速度峰值39.08 mm/s2时开始脱落；同一激励下，虽然各个果实位置不同，但它们振动特性变化趋势相同。该研究可为防脱落采摘机构参数设计提供理论依据。

振动；力学模型；脱落特性；有限元分析；葡萄；动态响应

0 引 言

近年来中国葡萄产业发展迅猛，自2004年以来鲜食葡萄种植面积已持续居于世界第一[1]。但是当前国内鲜食葡萄收获基本靠人工采摘，劳动强度大[2-3]。随着国内人口老龄化日趋严峻、劳动成本上升，如何实现果实低损高效采摘成为农业生产亟待解决的难题[4-5]，机器人采摘葡萄主要通过夹剪果梗来完成，然而，采摘过程中的剪切断梗振动激励易导致果粒脱落，因此研究果实在断梗激励下的振动脱落特性有重要意义。

夹剪式收获方式是目前果梗类植物果实的主要收获手段之一[6-9]。国内外针对葡萄采收机理的相关研究，主要集中在葡萄的目标识别[10-12]和收获机的试制[13-15]，Caprara等[16-17]通过对机器内部加速度和植物加速度的测量，研究了葡萄收获机械传递的压力对质量和损伤的影响。Corné等[18]设计了一系列试验来测量葡萄的材料特性，包括张力下的茎刚度和断裂强度、压缩下的浆果刚度以及浆果分离力。袁盼盼等[19-20]设计一种曲轴式振动脱粒收获装置，通过建立响应面数学模型优化，降低脱粒率同时增加了破损率，获取了影响作业效果的主要因素。Bu等[21]通过分析不同果实的采摘模式，揭示了张力参数是果梗分离的主导因素。Saowapa等[22]用图像分析评估分形维数差异的方法确定番石榴果实振动损伤脱落程度，为研究水果脱落提供了新的方法。Castro-Garcia等[23]通过调查了成熟果实和未成熟果实的频率响应差异性，发现选择机械收获的重要因素是水果的频率响应及更高的果实质量。罗陆锋等[24-25]为葡萄采摘机器人的防损采摘提供一种葡萄免碰撞包围体求解与自动定位方法，确定了夹持式收获的夹持点。李成松等[26-28]基于RSSR空间四杆机构及平面双摇杆机构分析了葡萄果实振动分离装置，得出了分离效果的主要影响因素是电机转速、振动位置和振动摇杆长度，且构建了果-蒂振动分离模型，通过搭建曲柄摇杆机构分离率测定装置，得到了葡萄果-蒂振动分离特性，为葡萄果-蒂分离研究提供基础。但研究多集中于水果响应与振动分离装置的研制，并没有进一步研究造成果实脱落的因素。耿效华等[29]研究了酿酒葡萄果实振动脱粒特性，通过正交试验得出了酿酒葡萄收获的最佳振动频率为4～4.5 Hz，当振动频率大于4 Hz时，由于果-蒂拉力对葡萄果粒的做功较小而脱落，为葡萄在采摘过程中的振动机械参数优化提供参考。

为研究断梗激励对果梗式植物采收影响，本文拟建立葡萄果实-果梗动力学模型，分析葡萄果实在此模型下的振动脱落特性。利用ABAQUS软件对建立的串型葡萄简化模型进行有限元分析，通过葡萄模态分析与仿真扫频分析，获取葡萄谐响应振动参数范围，从而确定断梗激励下果实颗粒临界脱落参数。并进行实验室断梗采摘试验，以期为夹剪式机构的设计与优化提供依据。

1 葡萄果实-果梗动力学模型

1.1 葡萄果实-分梗动力学模型的建立

由于夹剪断梗一体化采摘方式在断梗过程中会产生振动激励，促使串型葡萄果实相对于主分梗连接处相对移动，引起的振动可能导致果实的无规则脱落。葡萄生长环境较为复杂多样，果实果梗处连接极软，多生长于枝繁叶茂的遮挡处，且不同品种葡萄生长状态不同，垂直悬挂生长在葡萄藤枝干上的葡萄，在剪断主梗过程中受振动激励影响在平面内发生摆动，竖直平面内的葡萄移动可简化视为平面摆模型。根据实际生长情况，本文通过对果实-分梗平面摆模型进行理论分析，研究葡萄果实在断梗激励下振动脱落特性。

葡萄果实-果梗平面摆模型中的主分梗连接处（具有一定质量1）可以沿着位于葡萄果实运动平面内做水平直线运动。若忽略分梗和空气阻力对果实运动的影响，可将果实分梗视为刚性杆，果实视为球体，质心为，以果梗与主枝干连接处为原点，为水平方向，为垂直方向，建立平面摆模型，如图1所示。

势能为

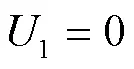
势能为

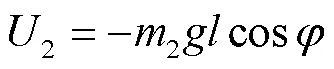
此时独立质点系动能为

势能为

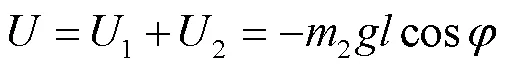
由上式中质点1和质点2动、势能可得拉格朗日函数为

即

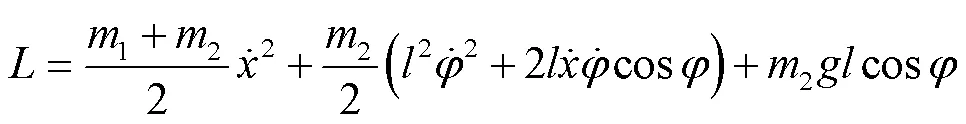
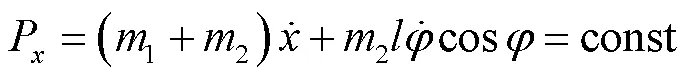
这表示系统质心在水平方向上静止，利用式（9）能量可写成

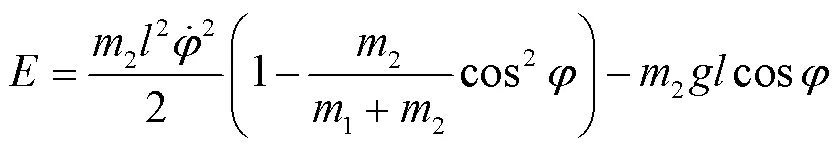
由此可得摆动时间

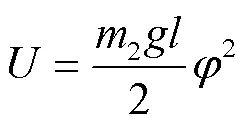
由此得频率

由此知：断梗激励下果实获得的振动频率与主梗分梗连接处质量、果实质量、分梗长度有关。

1.2 葡萄果实-果梗分离条件

由于果实硬度随着成熟度的变化呈各向异性，不同生长状态下的葡萄果实与分梗之间的结合力不同且呈非线性变化，结合力不仅与果实成熟度有关，还与整串葡萄的质量分布、光照面积、生物本体、内外轮廓有关。当断梗激励能量由断梗处经主梗-分梗-果实三级传递至各果实处，果实自身的惯性力与重力非线性叠加使得果实摆动。

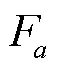
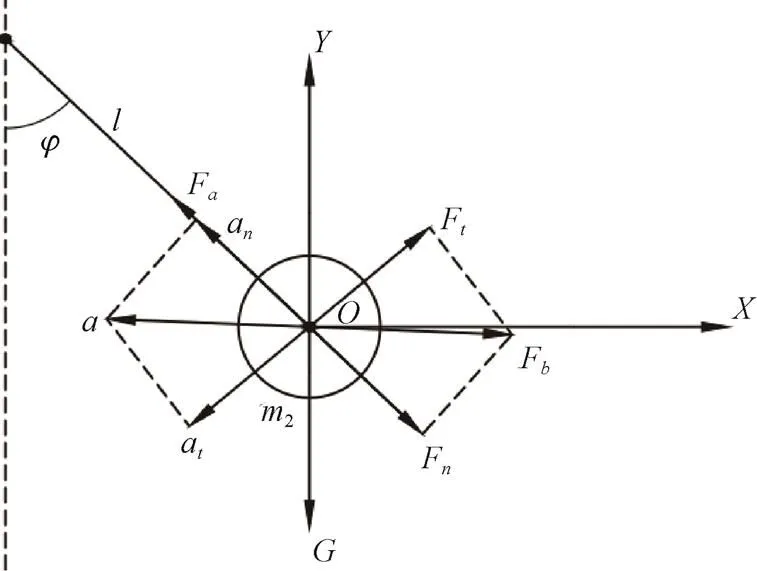
注：为单粒葡萄质量，kg；为果实与分梗连接力，N；为葡萄果实惯性力，N；为葡萄果实法向惯性力，N；为葡萄果实切向惯性力，N；为重力，N；为果梗长度，m；为葡萄粒加速度，m·s-2；为葡萄果实法向加速度，m·s-2；为葡萄果实切向加速度，m·s-2。

根据几何关系有

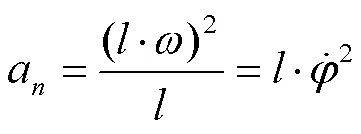
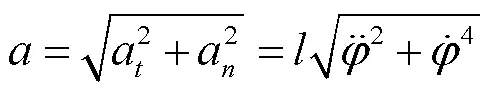
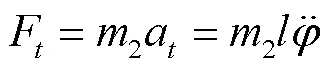
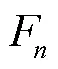
葡萄断梗式采摘中，颗粒自身产生的惯性力的法向分力促使果实脱落或有脱落趋势，葡萄果实质量很小，故忽略重力，简化为

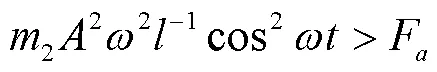
式中为强迫振幅，mm。

2 葡萄有限元建模及结果分析

2.1 葡萄振动试验材料与方法

为了验证理论分析的正确性，研究葡萄果实-分梗平面摆模型系统夹剪式收获过程中葡萄颗粒脱落特性，采摘作业时剪断果梗的激励可能使果实从植株果梗上脱落，为实现“减振低脱”的高效采摘就要防止果-蒂分离，因此需研究果梗振动激励传递及果实颗粒的动态响应特性。

2.1.1 试验仪器及设备

葡萄基本参数测量仪器：乐清市艾德堡仪器有限公司制造的GY-4型果实硬度计测量葡萄果实表面硬度，量程0.2～15 kg/cm2，示值误差±0.5%，测试行程70 mm；宁波得力集团生产的得力DL91200数显游标卡尺测量葡萄长度，测试范围0～20 mm，误差≤0.03 mm；希玛AR63A测量葡萄响应速度，测试范围0.1～199.9 mm/s；上海芈坤实业有限公司生产的高精度珠宝秤测量葡萄及果实质量，称质量范围0.01～1000 g，测量精度0.01 g；

数据分析软件：SolikWorks2020三维建模软件，ABAQUS6.14-4仿真软件，MATLAB 2016数据分析软件，

Origin 2021图像制作软件。

2.1.2 葡萄果实物理特性参数测定

于2021年8月11日成熟期随机选择在广东广州太和镇头陂村葡萄园刚采摘到的形状、质量、表皮颜色、颗粒饱满度、成熟度、颗粒硬度相近，且表面无损伤的类圆形夏黑葡萄颗粒。依次测量葡萄主要物理特性参数，所有数据测量后取平均值，葡萄主梗平均长为214.44 mm、直径为4.989 mm、分梗长为15.3 mm、直径为2.54 mm、果蒂直径为5.32 mm；葡萄颗粒平均纵向直径为28.99 mm、赤道直径26.45 mm；平均质量是20.01 g；选取的成熟葡萄平均硬度是9.44 kg/cm2；果梗质量是7.53 g。

2.1.3 试验方法

多颗粒鲜食葡萄摆动过程中存在非线性挤压与非规则约束性包围体碰撞，为研究果实受振后的响应状态先探索单颗粒果实再进一步研究串型葡萄。首先利用SolikWorks2020三维建模软件对已测绘的葡萄进行建模，使用ABAQUS6.14-4仿真软件对葡萄进行有限元分析，分析断梗激励下单颗果实响应状态并进一步获取串果模态分析，最后结合模态叠加下的扫频分析葡萄颗粒的脱落状态。

主梗-分梗-果实三级枝在实际振动传递中视为三级传递，自断梗处传递而下的能量呈衰减趋势，即离激振源越远振动幅度能量越小，而果-梗连接处欲获得“脱落角速度”需持续性激振能量。实际采摘作业中串型葡萄果实颗粒均受到不同程度的激振能量，且脱落效果与成熟度、振动传递距离、果梗连接处本体属性有密切关系，因此为贴近实际采摘作业需保证在断梗激励峰值下研究此三级激振传递频率变化。根据葡萄果梗-果实理论分析分离条件知断梗激励应满足：

1）为获得脱落颗粒的“脱落频率”，所施加的断梗激励需使得果-梗连接处获得脱落角速度，由于葡萄果梗生物体形态变化造成重复试验后直径的变化，故选取多串葡萄获取合适的断梗激励。

2）为保证果梗生物体形态完整性而施加合适的断梗激励，依据试验目的选取多种直径、多种环境下葡萄串样本进行试验。

2.2 单颗粒有限元分析

2.2.1 单颗粒建模

葡萄颗粒仿真建模时，果实果梗和果实果实之间在非结构环境下存在诸多非线性无规则挤压碰撞且有非线性蠕变，葡萄与葡萄颗粒之间、葡萄与分梗连接处存在多处干涉[30]。由于串型葡萄的分布形态（单串、重叠、贴靠和遮挡等）复杂，故将葡萄果实划分为多个相互独立且各向同性、均匀的线弹性圆球，圆球形态如图 3所示。

通过ABAQUS6.14软件对葡萄颗粒进行有限元分析，分析葡萄主梗在不附加任何约束下的振动激励状态，果梗果实形变结合模态云图仿真结果分析葡萄响应的一致性。

2.2.2 结果与分析

实际采摘过程中，由于剪断果梗引起的“断梗振动”经断梗处产生经夹持力处传递至果实，使果实在自由初状态下获得激振能量产生惯性力，从而使得果实发生相对移动，当果实惯性力大于果柄作用力时果实脱落，因此葡萄的采摘试验主要集中于果梗的断梗激励、模态频率以及受迫振动以后果实动态响应参数的获取。获取葡萄的摆动响应状态就可预测果实在此频段内的断梗激励振源作用下产生的实际振动响应。

通过分析葡萄主梗在不附加任何约束下的振动激励状态与果梗果实形变过程，验证了果梗模型的正确性。研究在断梗激励下葡萄果实不同振幅状态下的谐响应，在此基础上分析串型葡萄在断梗激励下的脱落规律，为实现最优剪切夹持参数、减振低脱、提高果实质量提供理论基础。

2.3 串果有限元分析

鲜食葡萄具有蠕变特性，不可能准确的用一组方程来描述非线性的葡萄变化全过程。因此首先建立串型葡萄的三维仿真模型将建模的多颗粒葡萄简化为14个颗粒，减少颗粒之间的非线性挤压从而提高模型精度，然后做有限元分析，进而找出葡萄颗粒在断梗三级激励振荡下的变化趋势与响应状态。

振源处激励使得果实获得超出本体与果实之间叠加的固有频率的响应频率从而发生相对移动。考虑到主梗剪切力提取与葡萄颗粒之间关系不大，所以用质量点来代替葡萄的质量。将几何模型导入ABAQUS软件，建立有限元模型。经查阅相关特性如表1所示。对果梗、果实等不同材料分别设置不同的材料属性，同时保证各个环节的网格彼此之间存在关联。

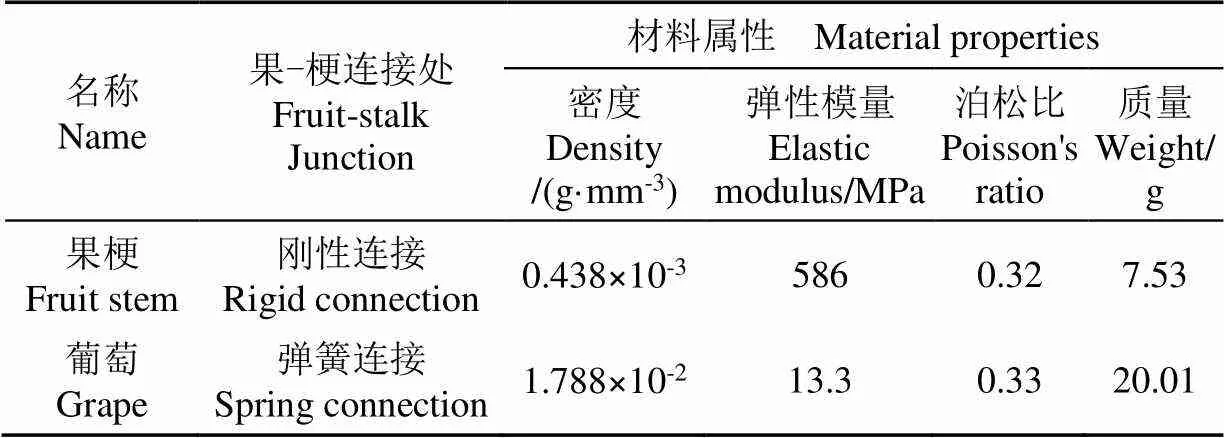
表1 模型各部分材料参数

材料本构赋予：果梗属于非金属非完全线弹性，确定最合适的材料属性。

工况施加：在果梗合适位置施加强制位移，同时约束最上方果梗以及夹持位置。

经试验测定葡萄主梗直径为5 mm左右。

2.3.1 剪切力及夹持力

图4a为在剪切断梗过程中，剪断果梗的横截面无数剪切力的集合力，图4b为断梗过程中位移与时间的曲线。从曲线中可看出随着时间增大剪切力呈递增趋势，在接近0.015 s时果梗被切断，即断梗剪切力为6.454 N，在此之后剪切力大小衰减至0，而在此过程中由于夹剪机构的工作引起果梗本体摆动产生的位移亦呈递增趋势，与实际较为符合。

为获取夹持参数，特固定葡萄梗方向的转动，考虑到主梗夹持处为类圆柱形和夹持两截面分力的采集，实际生产作业中为先夹持后剪切，因此施加使左右两侧分别向轴线方向压进的强制位移1 mm使其夹持住（有预紧力的效果），在仿真试验中为方便分析使两截面的力聚集于一处。

图5为剪切夹持过程中夹持力与时间的变化曲线，从曲线中可知：垂吊生长于藤蔓上的葡萄初始夹持力（预紧力效果）3.3 N。在断梗振动一级传递至夹持处过程中产生较大波动引起果梗无序摆动，从而促使夹持力呈无规则变化，最大的夹持力约为6.4 N。改变剪切角度或增大夹持力会影响断裂。

2.3.2 葡萄果实模态分析

为揭示变载荷作用下串型葡萄果实蠕变摆动的振动特征，建立了能反映串型葡萄的振动响应应变模型，对蠕变相对剪切位移、响应速度与响应加速度进行分析。考虑到固有频率的提取与葡萄质量、连接刚度、振型（特征向量）以及葡萄外形有极大关系，故将实体建模的葡萄简化为统一的球体，如图6所示。

断梗激励三级传递至各个受振果实点，激振力频率由0开始逐渐增大，达到各个果实固有频率时，初始果实颗粒统一静止状态被破坏，呈现出不同于以往稳定状态（静止）的差异性，同时考虑到质量、刚度、阻尼等因素，为精确求得断梗激励下葡萄18阶模态频率与振型。如图7所示。

葡萄前18阶固有频率的计算值如表2所示。分析知：在非平稳振动激励下，断梗振动激励三级传递过程中出现无规则随机振动，其中1～3阶，6～18阶均表现为葡萄颗粒不同程度的摆振，4～5阶表现为下部颗粒与果梗一同摆动。而从多阶频率看出10、11阶表现为单颗振动为主，同时伴随着多颗振动；14、17阶表现为多颗绕着主梗扭转振动；其他阶数表现为葡萄颗粒不同程度的摆振。通过葡萄模态分析，观测相应果实的位移状况及观测点的位移达到最大所对应的固有频率，找出果实摆动响应状态，就可以预测果实在此频段内的断梗激励振源作用下产生的实际振动响应。

结果表明：在断梗过程中果梗、葡萄摆动具有明显的非线性形变和位移加速蠕变趋势，果实实际的振动形态并不是一个规则的形状，而是各阶振型相叠加的结果。振动幅值变量在发生共振时最大，而在不同振动互相抵消时最小，同时随着时间的延续，振动幅度也逐渐增大。

2.3.3 葡萄果实模态叠加下的扫频分析

采摘系统的频率响应显示葡萄梗植株的某些属性，以频率形式输入的激励产生响应函数，能够形象反应在剪切力引起的振动下的脱落颗粒的频率变化状态与激励下非线性响应。每个颗粒在同一激励下有不同的振动形态，因而为了生成断梗激励下频率响应曲线，对模型进行模态叠加下的扫频分析；也就是对不同频率下多颗粒状态进行求解，获取频率响应曲线中与系统固有频率对应的不同峰值与振动形态。对简化模型施加6.454 N剪切力，扫频得到串果响应。第一颗脱落的葡萄颗粒如图8。

通过对葡萄振动模型进行谐响应分析，确定了串型葡萄在固定幅值的正弦位移作用下的稳定响应。根据夹剪式振动收获振幅特性，由模态分析仿真结果设定扫频频率范围为0～25 Hz，进行谐振动分析可得到葡萄在此激励源下位移、速度、加速度值变化曲线。

通过模态的谐响应分析，葡萄果实颗粒在频率为4 Hz时位移最大开始脱落，即在持续断梗激励下传递至葡萄果实开始脱落时的主频率即脱落频率为4 Hz。不同果实的脱落特性大致相同，如图9所示。

由图10可看出：颗粒呈无规则振荡，在分梗-果实接触处的激振频率约4 Hz时，发生速度约为0.92 mm/s、加速度约为39.08 mm/s2的突变，且在此之后逐渐归于平静，此时葡萄果实加速度产生的离心力近似等于成熟果实-分梗结合力，即此突变频率为该颗粒“脱落频率”。

0～4 Hz振动频率区间内，一二级传递中出现较大幅度的摆动，受振点处具有加速度峰值39.08 mm/s2，速度峰值0.92 mm/s，此时最大摆动幅度为49.88 mm；4～5 Hz振动频率区间内，主—分梗连接处存在较大阻值，此时谐响应呈衰减趋势，从一二级峰值衰减至加速度为5.38 mm/s2，速度为0.22 mm/s，此时摆动幅度为5.99 mm；超过5 Hz振动频率值时，三级传递至果-梗结合处激振能量逐渐消失系统趋于平稳，即采摘振荡后葡萄慢慢归为静止，此时加速度、速度、位移亦为0。整个采摘周期过程结束。

在三级传递中的复杂应力状态下果梗果实初始状态出现改变，对应力状态的分析（图11）知：

1）某颗粒在频率约14 Hz时应力应变达到最大，此时果实发生的形变也最大。

2）应力应变有多复合振动影响，既有自己本身固有频率影响，又有振动频率和其他颗粒振动频率的影响。由于果梗受激振频率影响，发生外曲线形状断裂等各种形变。果梗材料具有弹性变形性，在持续激励下超出固有频率达到临界频率时，果梗发生塑性变形直至破坏，由局部变形积累至断裂形变。

根据图10b与图12对比知：当振动激励传递至三级果梗果实处，均在4 Hz左右达到速度峰值为0.67 mm/s时脱落，葡萄颗粒与第三方碰撞呈振荡趋势。同一断梗激励下，不同位置果实的速度都是先随着激励时间增加而增大，虽然受位置影响速度大小略有不同，但振动特性曲线整体变化规律和趋势一致，即不同颗粒在断梗激励下脱落频率均约为4 Hz。

3 振动试验分析

3.1 葡萄夹剪式采摘试验

为获取振动临界脱落参数，优化夹剪机执行器，结合ABAQUS仿真实验结果，于2021年8月成熟期随机选择刚采摘的外观类似的串型葡萄在佛山科学技术学院农业机器人实验室进行采摘振动试验。利用葡萄夹剪式采摘试验平台对串型葡萄施加持续性的断梗激励，研究在激励下葡萄不同颗粒的振动时间与响应频率、速度等“振动脱落特性”参数的关系。选取无杂叶、无遮挡葡萄悬挂于平行于地面的圆柱形悬梁上，将自制夹剪机夹持器与测振仪安装于大族机械臂末端，夹剪机构与地面平行且垂直于主梗，如图13所示。

1.机械臂 2.测振仪 3.夹剪机

结果如表3知：在持续断梗激励下，葡萄果实相对于各自分梗结合处的最大摆动速度约为0.9 mm/s时脱落，与扫频结果大致相同。葡萄采摘断梗过程中振动是多级非线性动态传递，串型葡萄生长环境复杂性及颗粒分布的不均匀性会造成结果的差异性，故分析ABAQUS仿真试验结果并结合采摘前后葡萄颗粒数量变化，进一步分析脱落频率对颗粒的影响。

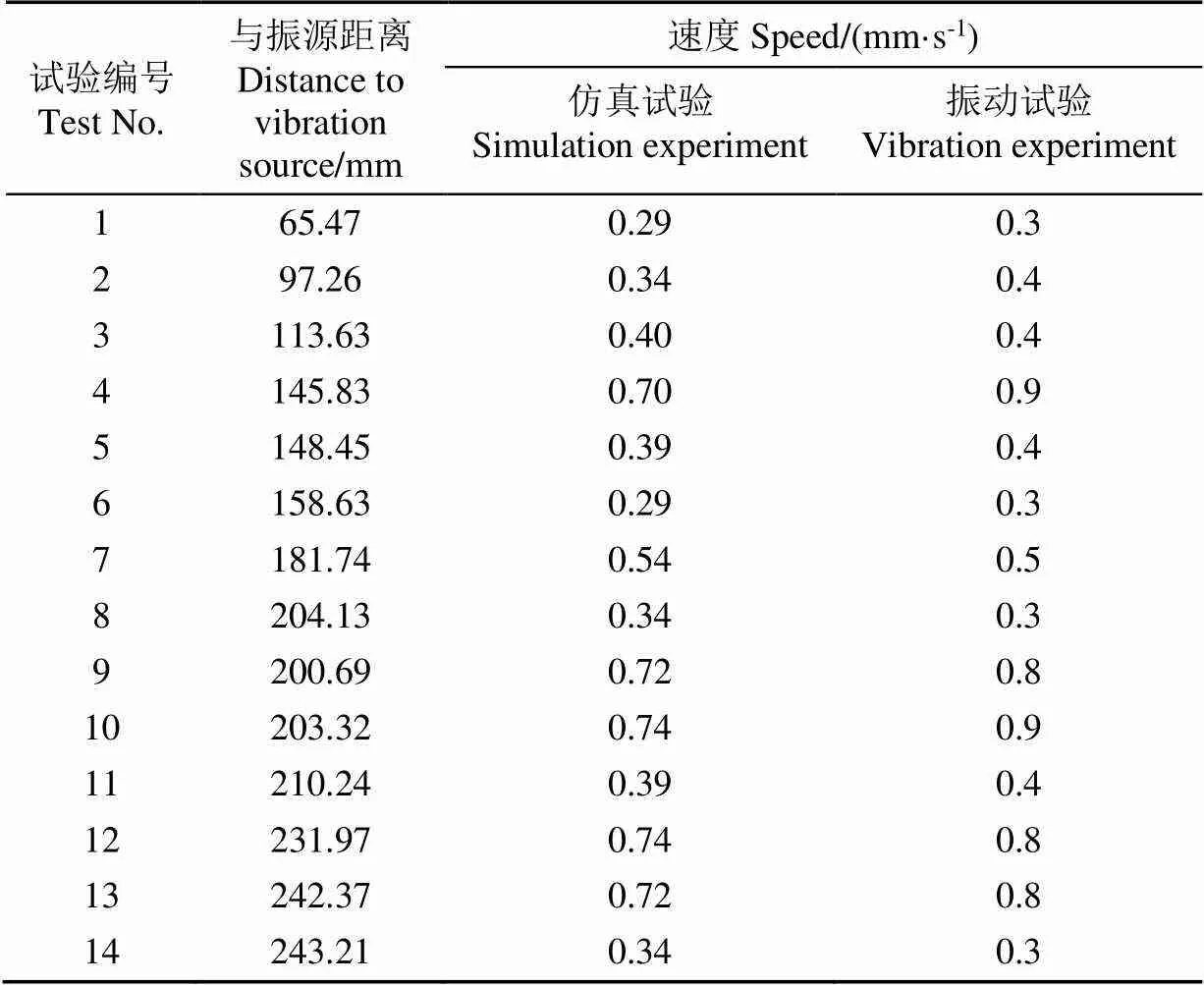
表3 断梗激励下果实响应结果对比

3.2 采摘试验分析

“采摘质量”是果实价值的重要体现，尽可能减少采摘过程中执行器末端与葡萄果实间的双侧约束性夹持碰撞，即外侧碰撞损伤。实现在手抓指面或指尖从接触果实到完成可靠夹持过程的夹持力控制，从而避免夹持力过大造成葡萄表面损伤，并且由于压缩载荷的作用而产生接触应力、受力不均、表皮硬度较小也会造成果实不同程度损伤。若启动加速度过大亦会造成瞬间载荷增大引起机械振动影响试验效果。

试验时发现，采摘过程中的断梗激励大小决定实验结果是否满足实际采摘需要，断梗激励过大会破坏果梗生物结构造成无法剪断，过小则果-梗连接处无法获得脱落角速度或葡萄直接掉落。为准确研究葡萄振动脱落特性，需研究断梗激励峰值下的三级激振传递频率变化。

1）为求主级梗动态响应状态，对剪切处施加断梗效果的激励，采集出夹持状态下主梗加速度响应。

2）为验证主-分梗二级相对位移变化，在试验过程中观察主-分梗生物体变化。

3）为求果-梗三级果实颗粒脱落特性，特以脱落果实作为标记点，研究在持续一段时间内脱落果实频率与应力应变、位移、速度、加速度等响应参数。选取多组样本分别进行试验。

3.3 仿真试验与采摘试验对比分析

仿真试验结合采摘实验分析振动的传递，此仿真模型以均匀分布的颗粒为振动研究对象，断梗峰值激励由断梗处向下经主梗-分梗-果实三级传递，根据传递等级及试验形态观察分析葡萄振动的各向异性表现：由于夹持力持续存在且距离断梗激励处距离较近，主梗振动幅度较小，而中部至根部果实分布增多、偏位移增大导致弯矩增加造成振动幅度较主梗顶端较大，突出表现为各向异性。“凸透镜式”分布决定整串质量的不均匀性，而且受光照及生物本体影响中下部外轮廓果实成熟度较大，实景采摘中的葡萄往往夹杂着坏果、杂叶、藤蔓等，一定程度上影响采摘质量与效率。但通过多组多样本实验观察对比观察分析知：虽然果园在非结构环境下采摘作业中葡萄的差异性导致振动响应与仿真试验存在一定误差，但葡萄果梗、颗粒总体振动响应趋势与采摘效果接近仿真试验。

4 结 论

1）建立了葡萄果实-分梗平面摆模型，通过提出拉格朗日函数进一步求得了系统总能量，从动力学角度揭示了摆动过程中果实参数变化，为研究果实临界脱落条件提供理论依据。

2）为便于研究问题建立多果实颗粒简化模型，对建立的简化模型进行ABAQUS有限元分析。提取了夹剪等输入信号，在0.015 s时提取最大剪切力为6.454 N，最大夹持力为6.4 N。

3）利用模态分析知断梗激励下葡萄出现无规则扭转摆动，各个颗粒表现各不相同。在0～20 Hz内，由模态叠加下的扫频分析知：葡萄果实“脱落频率”约为4 Hz，此时发生速率峰值约为0.92 mm/s、加速度峰值约39.08 mm/s2的突变，最大摆动幅度为49.88 mm；为保证分析的准确性，研究了第二脱落颗颗位移，发现在4 Hz左右达到最大而后振荡至平稳，三级传递至果-梗结合处激振能量逐渐消失系统趋于平稳，即采摘振荡后葡萄逐渐归为静止，整个采摘周期过程结束。与第一颗脱落果实振动特性曲线整体变化规律和趋势一致。

[1] 田淑芬，苏宏，聂松青. 2018年中国鲜食葡萄生产及市场形势分析[J]. 中外葡萄与葡萄酒，2019，224(2)：95-98.

Tian Shufen, Su Hong, Nie Songqing. Analysis on the production and market situation of Chinese table grape in 2018[J]. Sino-Overseas Grapevine & Wine, 2019, 224(2): 95-98. (in Chinese with English abstract)

[2] Bac C W, Henten E J, Hemming J, et al. Harvesting robots for high-value crops: State-of-the-art review and challenges ahead[J]. Journal of Field Robotics, 2014, 31: 888-911.

[3] 张德学，张军强，李青江，等. 我国葡萄全程机械化应用现状及发展展望[J]. 农业装备与车辆工程，2019，57(3)：17-22.

Zhang Dexue, Zhang Junqiang, Li Qingjiang. Current situation and development prospect of grape mechanization in China[J]. Agricultural Equipment & Vehicle Engineering, 2019, 57(3): 17-22. (in Chinese with English abstract)

[4] 赵春江. 智慧农业发展现状及战略目标研究[J]. 智慧农业，2019，1(1)：1-7.

Zhao Chunjiang. State-of-the-art and recommended developmental strategic objectivs of smart agriculture[J]. Smart Agriculture, 2019, 1(1): 1-7. (in Chinese with English abstract)

[5] 孙凝晖，张玉成，石晶林. 构建我国第三代农机的创新体系[J]. 中国科学院院刊，2020，35(2)：154-165.

Sun Ninghui, Zhang Yucheng, Shi Jinglin. Build innovation system of third generation of agricultural machinery in China[J]. Bulletin of the Chinese Academy of Sciences, 2020, 35(2): 154-165. (in Chinese with English abstract)

[6] Liu J, Yuan Y, Gao Y, et al. Virtual model of grip-and-cut picking for simulation of vibration and falling of grape clusters[J]. Transactions of the ASABE, 2019, 62(3): 603 – 614.

[7] Zhao Jian, Satoru T, Ma T, et al. Modal analysis and experiment of a lycium barbarum L. shrub for efficient vibration harvesting of fruit[J]. Agriculture, 2021, 11(6): 519-519.

[8] 许睿，赵明富，张利伟. 葡萄采摘机器人研究进展与展望[J]. 河南科技学院学报：自然科学版，2018，46(4)：74-78.

Xu Rui, Zhao Mingfu, Zhang Liwei. Research progress and prospects of grape picking robots[J]. Journal of Henan Institute of Science and Technology: Natural Science Edition, 2018, 46(4): 74-78. (in Chinese with English abstract)

[9] Liu M, Wang F, Xing H, et al. The experimental study on apple vibration harvester in tall-spindle orchard[J]. IFAC- Papers on Line, 2018, 51(17): 152-156.

[10] 罗陆锋，邹湘军，王成琳，等. 基于轮廓分析的双串叠贴葡萄目标识别方法[J]. 农业机械学报，2017，48(6)：15-22.

Luo Lufeng, Zou Xiangjun, Wang Chenglin, et al. Recognition method for two overlaping and adjacent grape clusters based on image contour analysis[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(6): 15- 22. (in Chinese with English abstract)

[11] 刘平，朱衍俊，张同勋，等. 自然环境下贴叠葡萄串的识别与图像分割算法[J]. 农业工程学报，2020，36(6)：161-169.

Liu Ping, Zhu Yanjun, Zhang Tongxun, et al. Algorithm for recognition and image segmentation of overlapping grape cluster in natural environment[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(6): 161-169. (in Chinese with English abstract)

[12] 苏仕芳，乔焰，饶元. 基于迁移学习的葡萄叶片病害识别及移动端应用[J]. 农业工程学报，2021，37(10)：127-134.

Su Shifang, Qiao Yan, Rao Yuan. Recognition of grape leaf diseases and mobile application based on transfer learning[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(10): 127- 134. (in Chinese with English abstract)

[13] 尹建军，陈永河，贺坤，等. 抓持-旋切式欠驱动双指手葡萄采摘装置设计与试验[J]. 农业机械学报，2017，48(11)：12-20.

Yin Jianjun, Chen Yonghe, He Kun, et al. Design and experiment of grape-picking device with grasping and rotary-cut type of underactuated double fingered hand[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(11): 12-20. (in Chinese with English abstract)

[14] 张佳喜，黄涛，王茂博. 单马达往复式葡萄剪枝机设计与试验[J]. 农业机械学报，2021，52(8)：106-116.

Zhang Jiaxi, Huang Tao, Wang Maobo. Design and experiment of single motor reciprocating grape pruning machine[J]. Transactions of the Chinese Society for Agricultural Machinery, 2021, 52(8): 106-116. (in Chinese with English abstract)

[15] 李超，邢洁洁，徐丽明，等. 柔性梳脱式酿酒葡萄脱粒机构设计与试验[J]. 农业工程学报，2015，31(6)：290-296.

Li Chao, Xing Jiejie, Xu Liming, et al. Design and experiment of wine grape threshing mechanism with flexible combing striping monomer[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(6): 290-296. (in Chinese with English abstract)

[16] Caprara C, Pezzi F. Measuring the stresses transmitted during mechanical grape harvesting[J]. Biosystems Engineering, 2011, 110(2): 97-105.

[17] Pezzi F, Caprara C. Mechanical grape harvesting: Investigation of the transmission of vibrations[J]. Biosystems Engineering, 2009, 103(3): 281-286.

[18] Corné J C, Stephanus G L. The destemming of grapes: Experiments and discrete element modelling[J]. Biosystems Engineering, 2013, 114(3): 232-248.

[19] 袁盼盼，朱兴亮，尤佳，等. 酿酒葡萄曲轴式振动脱粒收获装置研制[J]. 农业工程学报，2020，36(9)：67-74.

Yuan Panpan, Zhu Xingliang, You Jia, et al. Development of crankshaft vibration threshing and harvesting equipment for wine grape[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(9): 67-74. (in Chinese with English abstract)

[20] 张静，龙新华，韩长杰，等. 机械驱动式辣椒穴盘苗自动取投苗系统设计与试验[J]. 农业工程学报，2021，37(5)：20-30.

Zhang Jing, Long Xinhua, Han Changjie, et al. Design and experiments of mechanically-driven automatic taking and throwing system for chili plug seedlings[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(5): 20-30. (in Chinese with English abstract)

[21] Bu L X, Hu G R, Chen C K, et al. Experimental and simulation analysis of optimum picking patterns for robotic apple harvesting[J]. Scientia Horticulturae, 2020, 261: 108937.

[22] Saowapa C, Pattamaporn Y, Sujitra A, et al. Vibration damage in guava during simulated transportation assessed by digital image analysis using response surface methodology[J]. Postharvest Biology and Technology, 2021, 181: 111641.

[23] Castro-Garcia S, Roldán G L B, Ferguson L, et al. Frequency response of late-season 'Valencia' orange to selective harvesting by vibration for juice industry[J]. Biosystems Engineering, 2017, 155: 77-83.

[24] 罗陆锋，邹湘军，熊俊涛，等. 自然环境下葡萄采摘机器人采摘点的自动定位[J]. 农业工程学报，2015，31(2)：14-21.

Luo Lufeng, Zou Xiangjun, Xiong Juntao, et al. Automatic positioning for picking point of grape picking robot in natural environment[J]. Transactions of the Chinese Society of Agricultural Engneering (Transactions of the CSAE), 2015, 31 (2): 14-21. (in Chinese with English abstract)

[25] 罗陆锋，邹湘军，叶敏，等. 基于双目立体视觉的葡萄采摘防碰空间包围体求解与定位[J]. 农业工程学报，2016，32(8)：41-47.

Luo Lufeng, Zou Xiangjun, Ye Min, et al. Calculation and localization of bounding volume of grape for undamaged fruit picking based on binocular stereo vision[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(8): 41-47. (in Chinese with English abstract)

[26] 李成松，高振江，坎杂，等. 双支撑酿酒葡萄果实振动分离装置作业机理[J]. 农业工程学报，2015，31(4)：26-32.

Li Chengsong, Gao Zhenjiang, Kan Za, et al. Operation mechanism of double support vibration separation device for wine grape berry[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(4): 26-32. (in Chinese with English abstract)

[27] 李成松，高振江，坎杂，等. 酿酒葡萄果-蒂振动分离试验[J]. 农业工程学报，2015，31(9)：39-44.

Li Chengsong, Gao Zhenjiang, Kan Za, et al. Experiment of fruit-pedicle vibration separation of wine grape[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(9): 39-44. (in Chinese with English abstract)

[28] 李成松，坎杂，谭洪洋，等. 4FZ-30型自走式番茄收获机的研制[J]. 农业工程学报，2012，28(10)：20-26.

Li Chengsong, Kan Za, Tan Hongyang, et al. Development of 4FZ-30 self – propelled tomato harvester[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(10): 20-26. (in Chinese with English abstract)

[29] 耿效华，徐丽明，李超，等. 酿酒葡萄果实振动脱粒特性研究[J]. 农机化研究，2018，40(5)：147-152.

Geng Xiaohua, Xu Liming, Li Chao, et al. Study on the vibration threshing characteristics of wine grapes[J]. Journal of Agricultural Mechanization Research, 2018, 40(5): 147-152. (in Chinese with English abstract)

[30] 王荣，焦群英，魏德强，等. 葡萄的力学特性及有限元模拟[J]. 农业工程学报，2005，21(2)：7-10.

Wang Rong, Jiao Qunying, Wei Deqiang, et al. Mechanical characteristics and the finite element analysis of grapes[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(2): 7-10. (in Chinese with English abstract)

Vibration shedding characteristics of the grapes under the excitation of broken stems and experimental research

Yan De, Wang jianxiao, Luo Lufeng※, Liu Wentao, Wei Huiling, Wang Jinhai, Liu Baoli, Lu Qinghua

,,528000,

Fruit particle shedding can be often caused by the vibration excitation of broken stems in the clip-cut grape picking. In this study, a dynamic model of the fruit-stem-dividing plane pendulum in the vertical plane was first established, according to the actual growth of grapes. The theoretical angular velocity of fruit shedding was then deduced under the excitation force of the broken stem. After that, the critical condition was determined for the separation of the fruit-stalk swing and falling off, where the swing trajectory was actually a part of the circular motion. In research objects, the freshly picked round grapes were collected to survey with a similar appearance, maturity, and no damage on the surface. The main physical characteristics of the grapes were also measured at the ripening stage in turn. Specifically, the average length of the main stalk of grapes was 214.44 mm, the average longitudinal diameter of the grape berries was 28.99 mm and the equatorial diameter was 26.45 mm; the average weight was 20.01 g; the average hardness was 9.44 kg/cm2; the weight of the stalk was 7.53 g. In a simulation, a SolikWorks2020 three-dimensional modeling software was utilized to model the grapes. Then the ABAQUS software was used to analyze the dynamic response and swing trend of a single grape under the excitation of broken stems. As such, the swing and deformation trends of a single grape were determined under the excitation of broken stems without squeezing. Since there was much squeezing between the grape particles, the model was simplified to 14 independent, isotropic, and uniform linear elastic spherical particles. The main shearing stem was also applied for the simplified clamping model, thereby collecting the input information, such as the shear force, and the clamping force under the excitation of the broken stem. The simulation test showed that the shear force was 6.454 N when cutting the main stem, and the clamping force changed from the initial 3.3 N to the maximum 6.4 N. The finite element analysis was then performed on the vibration using the simplified model of cluster grapes. A dataset was thus obtained, including the displacement, velocity, acceleration, as well as the stress and strain of the grape fruit relative to the junction of the fruit stalk at the moment before falling off. An optimal combination of parameters was achieved to determine the critical vibration shedding of the grapes. In the 18-order modal analysis, the vibration excitation was transmitted to the vibrated fruit via the main stem-sub-stem-fruit three levels, where the fruit particles appeared the indefinite anisotropic torsional swing. Specifically, the 0-25 Hz sweep frequency was selected for the whole bunch of grapes under modal superposition. Consequently, the frequency of the vibrated fruit suddenly changed to a peak frequency of 4 Hz, and then rapidly attenuated to 0 under the excitation. The maximum swing amplitude of the vibrated fruit was 49.88 mm, the peak velocity was 0.92 mm/s, and the acceleration peak was 39.08 mm/s2, ranging from the shedding and then gradually decay to 0 in a picking cycle. The vibration frequency of the fruit particles presented a great mutation over their own natural frequency. At this time, the tertiary fruit-stalk junction was broken to cause the particles to fall off. The trend of vibration was the same under the same excitation, although the position of each fruit was different. The finding can provide a theoretical basis for the parameter design of anti-shedding picking.

vibration; mechanics model; shedding characteristics; finite element analysis; grape; dynamic response

闫德，汪建晓，罗陆锋，等. 断梗激励下葡萄果粒的振动脱落特性与试验[J]. 农业工程学报，2021，37(22)：31-40.doi：10.11975/j.issn.1002-6819.2021.22.004 http://www.tcsae.org

Yan De，Wang Jianxiao，Luo Lufeng，et al. Vibration shedding characteristics of the grapes under the excitation of broken stems and experimental research[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(22): 31-40. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.22.004 http://www.tcsae.org

2021-10-21

2021-11-15

国家自然科学基金资助项目（No.32171909，51705365）；广东省基础与应用基础研究基金（2020B1515120050，2020A1515111056）；广东省普通高校科研项目(2019KTSCX197，2018KZDXM074，2020KCXTD015)，

闫德，研究方向为采摘机器人。Email：yd_zcyy@163.com

罗陆锋，博士，副教授，研究方向为采摘机器人、机器视觉等。Email：luolufeng617@163.com

10.11975/j.issn.1002-6819.2021.22.004

S225.93

A

1002-6819(2021)-22-0031-10