江西省降水空间插值方法适用性分析

占龙飞 ， 陈佳义 ， 李 婕 ， 赵冠男 ， 胡菊芳

1. 江西省气候中心， 江西 南昌 360096

2. 淮安市淮阴区气象局， 江苏 淮安 223300

3. 江西省气象台， 江西 南昌 360096

0 引 言

降水是十分重要的气象要素，气象站观测的降水数据仅代表其所处位置有限范围内的降水状况，受经济、地形、观测技术和台站分布等客观条件限制，气象台站降水数据难以满足科研业务需求。高空间分辨率的降水数据在气候评估、地质灾害预警预报、水资源管理等方面具有巨大的应用价值。

为获取降水量的空间分布，通常结合统计学和地理信息科学将已知站点的观测数据进行空间插值。近年来，一些学者围绕降水数据插值方法的比较展开了一系列研究。一些学者(王国泰等,2018;王天华,2018;张仁平等,2018)对比了几种常用插值方法，选出了适合研究区域的最佳降水插值方法。降水受地形条件尤其是高程的影响较大，通常高程越高降水越大(Daly et al,2008)，基于地理因子的降水插值方法受到研究者们的关注。李丽娜(2009)引入地理影响因子的多元回归插值结果能较好地反映降水的整体分布和局部细微特征。蒋育昊等(2018)对比了不同插值方法在北京西北山区的应用效果，结果表明PRISM(Parameter-elevation Regression on Independent Slopes Model)插值模型比其他插值方法更能精确地表达降水的空间分布。

每种降水插值方法均存在局限性，同一种插值方法在不同下垫面上的插值效果可能存在很大差别(彭彬等,2011)，同一地区不同时期可能适用不同降水插值方法。江西省地处季风区，东、西、南三面环山，北部为鄱阳湖平原，中部为丘陵和河谷平原，地形复杂多样，高程梯度大，复杂的地貌特征致使降水分布呈现空间不均匀、局地性强等特点。本文基于数字高程模型(DEM)，对江西省的地貌特征进行栅格化处理，提取影响降水空间分布的地理要素，建立多元线性回归插值模型和PRISM降水插值模型，并与传统的插值方法进行比较，讨论不同降水空间插值方法在江西省的适用性，以期为江西省气候资源的定量分析与评价提供技术支持。

1 资料与方法

1.1 资 料

降水资料来源于江西省气象信息中心，经数据质量控制，剔除相应时段内缺测、空白及异常率高于1%的站点，最终筛选出1981—2020年江西境内有效的83个国家气象观测站逐日20—20时降水数据。83个国家气象观测站分布江西全境，海拔介于21.1—1 164.5 m，其中位于海拔200 m以上的有15站，100 m以下的有45站。站址长期稳定且四周空旷平坦，保证了观测数据的连续性和代表性。

DEM数据采用Albert投影，空间分辨率为500 m，包含经度、纬度、海拔、坡度及坡向等地理信息。站点地理位置及江西省地形高程如图1所示。

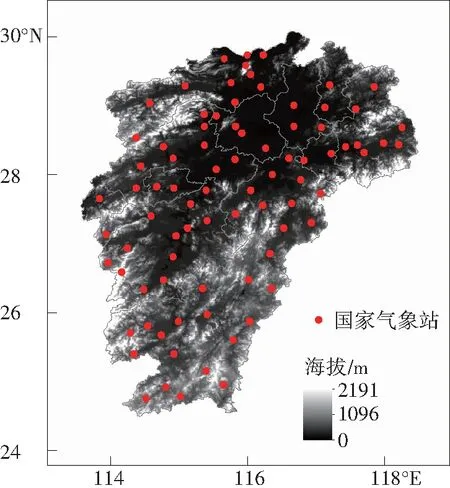
图1 江西省地形高程及83个国家气象观测站点分布

1.2 研究方法

空间插值方法的理论依据是Tobler地学定律，即根据已知的离散数据或分区数据，按照特定的数学关系推求出其他未知点或未知区域的数据(马秀霞等,2017)。实际应用中，以传统的反距离权重法(Inverse Distance Weighted，IDW)和克里金插值法最为常见(蔡迪花等,2009;王丽等,2015)。文中将以上2种传统插值方法与基于DEM的多元线性回归(Multiple Linear Regression，MLR)插值方法和PRISM插值方法进行比较，探讨4种降水空间插值方法在江西省复杂地形下的适用性。

1.2.1 反距离权重法

反距离权重法是一种基于相近相似原理的插值方法，用权重表示其影响程度，距离越大，对权重赋予权值越小，影响越小。计算式(占龙飞等,2018；黄少平等,2020)为

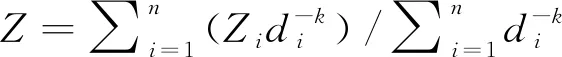
(1)

式中，Z为区域内未知点的值；Zi为第i个已知点的值；di为第i个已知点到该未知点的距离；k为指定的幂；n为区域内对未知点有影响(距未知点最近的n个站点均视为“有影响”)的已知点数，默认n为12。

1.2.2 普通克里金插值方法

普通克里金方法(Ordinary Kriging,OK)是较早被提出的克里金方法，是一个线性估计系统，适用于任何满足各向同性假设的固有平稳随机场。使用普通克里金插值方法时，需先计算样本变异函数，再根据样本变异函数的类型选择合适的变异函数理论模型进行模拟，最后根据模拟的变异函数对待估计点进行线性估计并给出估计方差作为不确定性的度量指标(彭彬等,2011)。

1.2.3 基于DEM的多元线性回归插值方法

研究表明，影响降水的空间分布因素主要有经度、纬度、坡度、坡向、海拔高度等(郭忆等,2013)。通过DEM各因子(经度X1、纬度X2、海拔高度X3、坡度X4、坡向X5)的有效组合能够更加精确地反映降水的空间分布。基于DEM的多元线性回归插值(MLR)模型公式(蔡迪花等,2009;王丽等,2015;占龙飞等,2018)为

PRE=aX1+bX2+cX3+dX4+eX5+ε

(2)

式中，PRE为降水量，a、b、c、d、e为回归系数，ε为残差项。

此外，为了应用方便，插值模型中的变量应尽可能少。因此，文中采用气候分析中应用广泛的逐步回归法，从一个自变量开始，按自变量对因变量作用的显著程度从大到小逐个引入回归方程，当先引入的变量由于后面变量的引入而变得不显著时，则将其剔除，从而建立“最优”多元线性回归插值模型。

1.2.4 PRISM空间插值理论模型

PRISM最早是由美国气象学家Daly等(1994)提出的一种基于地理空间特征和回归统计方法生成气候图的插值模型(Daly et al,1994)，该方法认为高程是影响气象要素分布的最重要因素(Daly et al,2002)。其中山区降水气象要素的基本规律是，随着海拔高度增加，降水量随之增加，当达到某一海拔高度后，降水量达到最大，这个高度为最大降水面，随后海拔继续增加，降水量随之减少(李慧晴，等,2021)。PRISM插值模型基于DEM数据，结合气象观测数据，建立加权线性回归方程，进行空间插值计算：

Y=aX+b

(3)

式中，Y为降水量插值结果；X为DEM栅格点上的高程值；a、b为回归方程系数。其中：

(4)

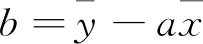
(5)

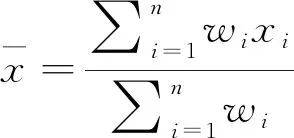
(6)

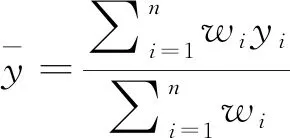
(7)

在降水量的插值回归模型中，各观测站点数据根据目标栅格空间位置分别赋予一个权重，根据站点气象观测值与对应的权重值计算出目标栅格的降水量。其权重值是多种因素的综合反映，表示为

W=f(Wd，Wz，Wc，Wl，Wf，Wp，We)

(8)

式中,Wd、Wz、Wc、Wl、Wf、Wp、We分别是距离、高程、站点聚类权重、垂直分层权重、地形趋势面权重、离海岸线距离权重和有效地形权重。考虑到研究区域的地理特点和资料限制的因素，本研究选取空间距离和高程2个因子，因此，调整后的综合权重计算公式如下：

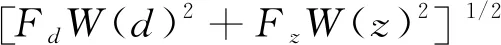
(9)

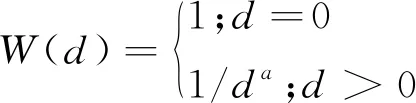
(10)

(11)

式中，W表示综合权重；W(d)和W(z)分别是空间距离函数和海拔高度权重函数。Δz是栅格与站点高程差的绝对值，Δzm、Δzx分别为最小、最大高程差，a、b分别是距离和高程权重指数。参数Fd、Fz、a和b分别设置为0.8、0.2、2和1(Daly et al,2002)。

1.3 精度检验方法

采用“交叉验证法”对反距离权重法、普通克里金插值法、多元线性回归插值方法和PRISM插值法进行精度检验。交叉验证的思路是，首先假定任一个气象站点降水量未知，采用剩余站点的观测值来插值估算，依次计算n次(n为站点数目)，最后计算所有站点实际观测值与估算值的误差，以此来对各种插值方法的优劣进行评估。常用于评价精度的参数是均方根误差(RMSE)。均方根误差反映样本数据的估值灵敏度和极值效应，值越小表明插值精度越高(蔡迪花等,2009; 王丽等,2015; 占龙飞等,2018)。RMSE的计算式：

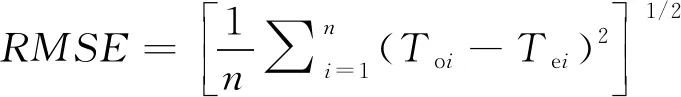
(12)

式中，Toi和Tei分别为第i个站点的气温观测值和气温预测值，n为站点数。

2 结果与分析

2.1 MLR插值模型结果

基于地理因子对江西省月和年降水量进行多元线性回归拟合，得到回归插值模型(表1)。模型决定系数R2为0.320 8—0.802 5，方程p值均小于0.05，说明该模型具有较好的回归相关性。分析表1可知，江西省月降水量和年降水量与地理因子显著相关，值得一提的是，逐步回归方程中并未出现坡度(X4)和坡向(X5)项。经进一步研究发现，坡度与海拔高度的相关系数为0.80(α=0.01)，两自变量之间存在近似线性关系，即存在复共线性关系，且坡度(X4)因子对插值模型的方差贡献率小于海拔高度(X3)因子，因此，坡度(X4)因子被剔除。另外，按国家气象站建站要求，气象站均建于平坦空旷地面上，各月及年降水量与坡向的相关系数仅为-0.07— 0.18，无法较好地反映出降水量与坡向的相关性，因此，坡向(X5)因子也被剔除。

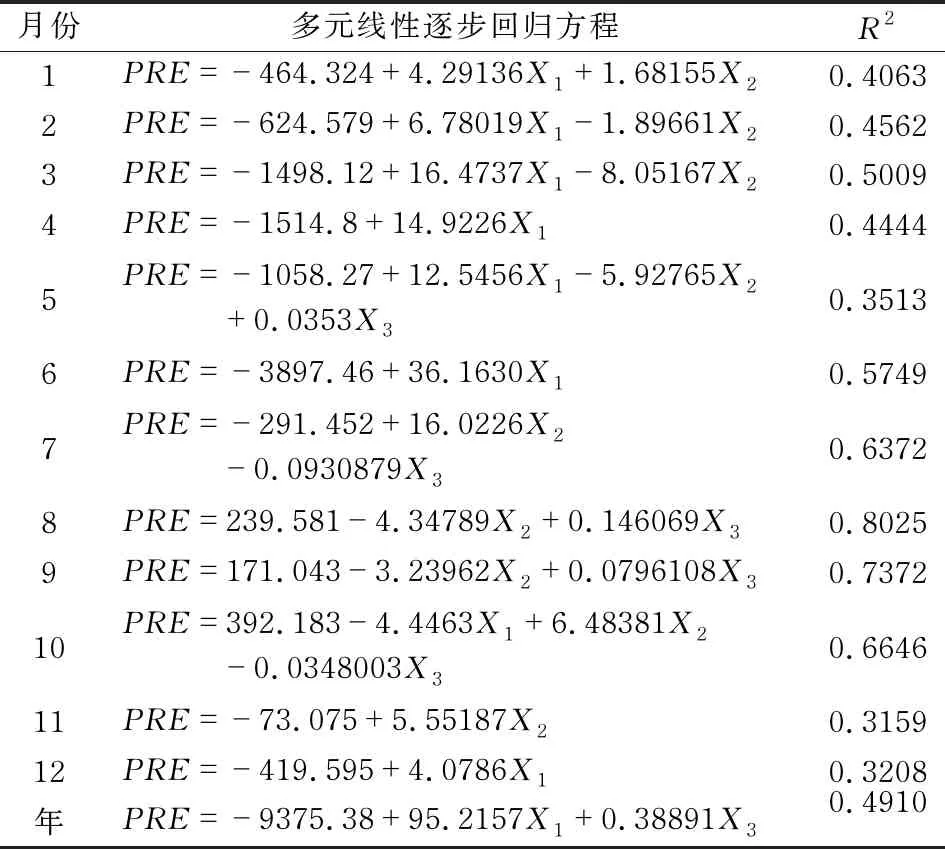
表1 1981—2020年江西省月和年降水量回归插值模型

通常来说，海拔高度与降水量具有一定的正相关性，但从江西省海拔高度与降水量的回归模型来看，仅在5月、7—10月和年降水量回归方程中出现了海拔高度因子(X3)，其中7月和10月出现了负相关性，这表明江西省降水垂直分布与海拔高度不一定呈正相关性。

2.2 插值精度分析

文中利用交叉验证方法比较不同空间插值方法的精度(图 2)，误差越小表明插值精度越高。分析可知，基于地理因子的MLR和PRISM插值模型精度在3—9月明显高于其他2种传统插值方法。传统插值方法在冬半年的插值精度略高于MLR和PRISM，这是由于冬半年降水量少，地形对降水量的影响不明显，使得MLR和PRISM插值方法的优势无法体现。从年降水量来看，4种插值方法的精度排序为PRISM>MLR>OK>IDW，PRISM插值精度分别比MLR、OK以及IDW分别高出12.3%、41.6%和44.7%。在降水量较大的月份(年)，PRISM和MLR的优势体现地更明显。

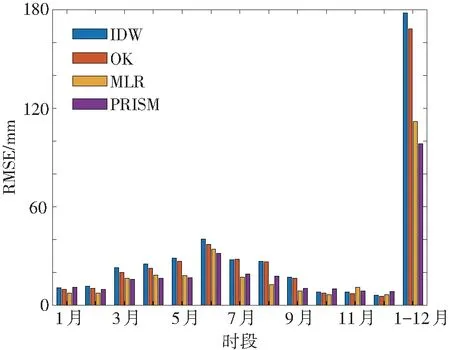
图2 1981—2020年江西省月、年平均降水量的4种插值方法交叉验证结果

为进一步研究4种插值方法在不同海拔高度的插值精度，考虑到江西省地势起伏变化大的特点，选取江西境内所有海拔高度大于300 m的国家气象站(共4个)，以及处于平均和最低海拔高度处各2个国家气象站点进行交叉验证，即依次从8个国家站中取出一个站，用剩余的82个国家气象站对该站点处的降水进行插值，交叉验证结果见图3。4种插值方法在300 m以下地区插值精度较高，但由于IDW和OK未考虑海拔高度对降水的影响，使得在高海拔地区插值精度远低于MLR和PRISM。综合来看，PRISM插值方法精度最高。

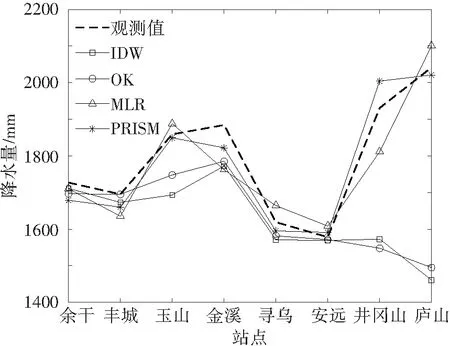
图3 1981—2020年江西省年平均降水量各站点预测值与观测值

2.3 插值效果对比

分别利用4种插值方法绘制1981—2020年江西省年平均降水量(图4)，图4a和图4b由Arcgis软件插值工具绘制，空间分辨率约为1.9 km，图4c和图4d基于DEM像元计算而成，空间分辨率为500 m。由图4可知，4种插值结果的降水量空间分布具有一定的相似性，赣东北、赣中东部降水较多，赣南、赣北北部相对较少。IDW和OK插值方法受站点空间分布影响极大，站点周边易出现降水值较周边区域显著大或小的奇异斑点(“牛眼”)，相较之下，IDW插值方法“牛眼”现象比OK明显；MLR和PRISM插值结果在准确展现江西降水空间分布的基础上，还能够精细地刻画出DEM各格点的降水空间分布特征，可以较好地反映出降水量与地形的关系，插值效果优于传统的IDW和OK插值方法。

图4 基于IDW(a)、OK(b)、MLR(c)和PRISM(d)方法的1981—2020年江西省年平均降水量

3 结论与讨论

基于1981—2020年江西省降水数据，在月和年尺度上对比分析了传统插值方法(IDW和OK)和基于DEM数据的空间插值方法(MLR和PRISM)在江西复杂地形条件下的插值精度和效果，得到以下结论：

1) 江西省5月、7—10月降水量与海拔高度存在显著的相关性，其中7月和10月降水量与海拔高度呈负相关，5、8、9月呈正相关。江西省月和年降水量与坡度、坡向无明显相关性。

2) 从插值精度来看，3—9月MLR和PRISM空间插值精度明显优于IDW和OK，而冬半年IDW和OK的插值精度略高于MLR和PRISM；4种插值方法的年降水量插值精度排序为PRISM>MLR>OK>IDW；PRISM和MLR在高海拔地区的插值精度远高于IDW和OK。

3) 从插值效果来看，4种插值结果的降水空间分布具有一致性，但IDW和OK方法易出现“牛眼”，同时无法体现地形对降水量的影响，总体来说，MLR和PRISM优于IDW和OK。

文中研究结果表明，MLR和PRISM空间插值方法能更精确地把离散点的数据内插到研究区域中，从而表现出气象要素空间分布特征，其优越性体现在气象要素空间分布与地形有强相关关系的插值计算中。由于降水空间分布还受到纬度位置(气压带或风带)、大气环流、海陆分布、人类活动等因素综合作用的影响，任何一种空间插值方法都无法完全表达气象要素的分布特征。每种空间插值方法有自身的适用性，应根据实际情况，选择最佳的空间插值方法。本文仅讨论4种插值方法在江西的插值精度和适用性，在今后工作中还应开展相应的机理研究。