基于动态资料的孔喉半径计算方法及应用

毛伟，余碧君

中国石油大庆油田有限责任公司勘探开发研究院，黑龙江 大庆 163712

孔喉半径是表征储层微观孔隙结构特征的一个非常重要的参数，孔喉半径越大，储层物性越好，渗流阻力越小，开发潜力越大；反之储层物性越差，开发潜力越小，开发难度越大，它决定了储层质量的好坏及开发潜力的大小[1-6]。目前，孔喉半径已成为低渗透储层、致密储层综合分类评价及开发效果评价选取的主要评价指标之一。

上述确定孔喉半径的方法均无法模拟地层原油的实际流动状况，因而得到的孔喉半径不具代表性,而目前也尚无从矿场动态资料角度研究孔喉半径的方法。为此，笔者从毛细管束渗流模型、等效渗流阻力原理出发，首次建立了基于动态资料的一维线性流动、二维平面径向流动的孔喉半径计算方法。

1 假设条件

由于孔隙结构的复杂性，实际渗流过程迂回曲折，为了便于分析，该次研究采用毛细管束渗流模型[16，17]求取孔喉半径，毛细管束渗流模型是实际油藏结构的简化，由n根半径相同的毛细管组成，其半径等价于实际油藏的孔喉半径，主要假设条件为:

1)毛细管束渗流模型与实际油藏的外观几何尺寸完全相同；

2)毛细管束渗流模型与实际油藏的孔隙体积相等，即孔隙度相等；

3)遵循等效渗流阻力原理，在相同的渗流条件(生产压差、流体黏度等)下，若毛细管束渗流模型与实际油藏的渗流阻力相等，则产量也相等。

2 一维线性流动孔喉半径

2.1 计算方法

设原油在横截面积为A、长度为L的油层中做一维线性流动，生产压差为Δp，根据毛细管束渗流模型的假设，用n根半径为rt的平行毛细管等效该流动过程(见图1)。

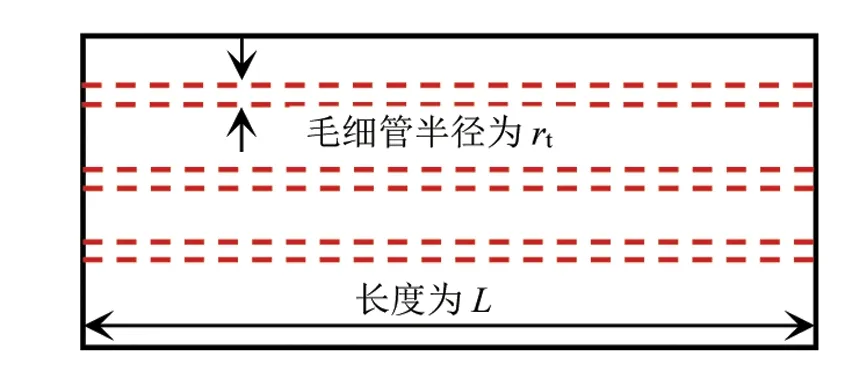
图1 一维线性流动毛细管束渗流模型示意图 Fig.1 Schematic diagram of capillary bundle seepage model for one dimensional linear flow

根据泊稷叶方程[17]，单根毛细管中的产量为:

(1)

根据假设条件2)，由孔隙度的定义:

(2)

得到毛细管数量:

(3)

总产量Qo等于毛细管数量乘以单根毛细管产量:

(4)

将式(4)变形可得到依据产量、生产压差动态数据计算的一维线性流动孔喉半径公式:

(5)

式中:qo为单根毛细管的产量，m3/d；rt为孔喉半径，μm；Δp为生产压差，MPa；μo为原油黏度，mPa·s；L为油层长度，m；φ为孔隙度，1；n为毛细管数量，根；A为油层横截面积，m2；Qo为总产量，m3/d。

2.2 验证公式

应用生产动态数据求出的孔喉半径是否准确，可通过以下方法进行验证。

根据一维线性流动达西定律[18]，实际油藏中的总产量为:

(6)

根据等效渗流阻力原理，由式(4)、式(6)得:

(7)

由式(7)变形得到:

(8)

式中:K为有效渗透率，mD。

式(8)为已知孔隙度、渗透率条件下的孔喉半径计算公式，若式(5)计算的孔喉半径与式(8)接近，则表明计算结果准确。

2.3 实际应用

根据文献[18]中的实例:原油在直径10cm、长30cm的砂管中做线性流动，已知φ=0.2，μo=0.65mPa·s，Δp=0.7MPa，K=200mD，Qo=0.4869m3/d。采用毛细管束渗流模型等效该砂管，外观尺寸不变，应用式(5)计算孔喉半径得:

根据式(8)计算孔喉半径为:

式(5)与式(8)计算结果相差无几，表明一维线性流动孔喉半径计算方法可行可靠。

3 二维平面径向流动孔喉半径

3.1 计算方法

设原油在供油半径为re、有效厚度为h的油层中做二维平面径向流动，生产压差为Δp，采用毛细管束渗流模型，用n根半径为rt的由供给边界指向井底的毛细管来描述该流动过程(见图2)。

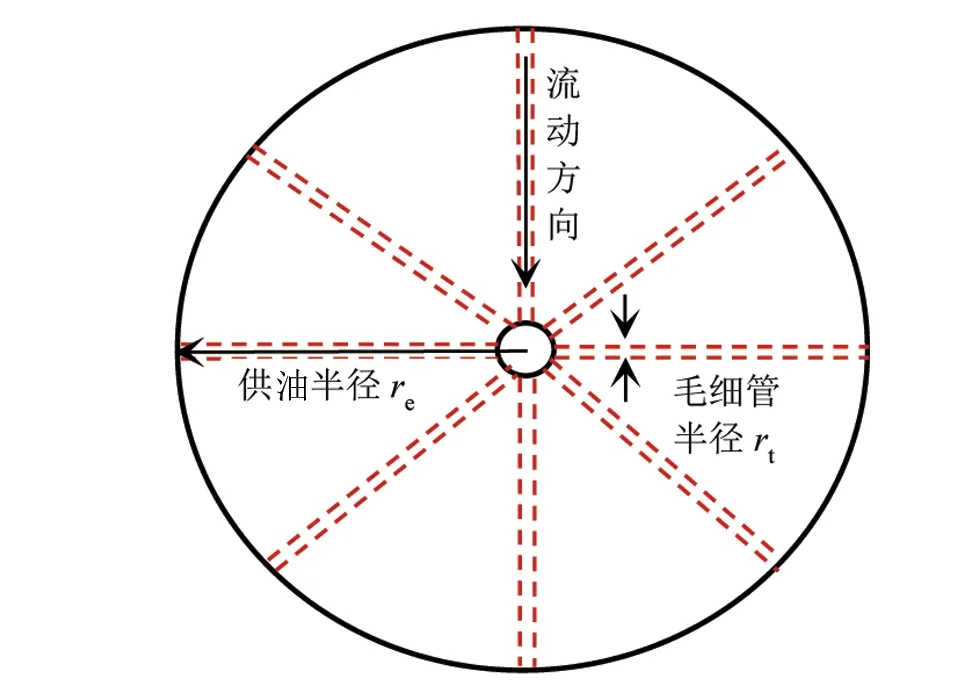
图2 二维径向流动毛细管束渗流模型示意图Fig.2 Schematic diagram of capillary bundle seepage model for two-dimensional radial flow

由毛细管束模型和实际油藏的孔隙度相等:

(9)

得到毛细管数量:

(10)

总产量为:

(11)

将式(11)变形得到依据生产动态资料计算二维平面径向流动孔喉半径的公式:

(12)

式中:re为供油半径，m；h为有效厚度，m。

3.2 方法验证公式

根据平面径向流公式[18]:

(13)

及等效渗流阻力原理，由式(11)、式(13)得:

(14)

变形得到:

(15)

式中:rw为油井半径，m。

若式(12)计算的孔喉半径与式(15)计算结果接近，则表明提出的二维平面径向流动孔喉半径计算方法是可靠的。

二维平面径向流动是油田开发过程中最常见的地层原油流动状态，式(12)中的各参数确定方法为:地层原油黏度取自高压物性取样分析结果，若没有进行高压物性取样，则可用文献[19]中给出的经验公式进行估算；射开有效厚度来自射孔通知单，射孔通知单中的有效厚度来自由测井曲线建立的油水层识别及有效厚度电性标准图版；孔隙度来自岩心分析结果或测井解释结果；油井产量取自油水井生产日报或月报；生产压差等于目前地层压力减去井底流压，目前地层压力由地层压力监测得到，或采用文献[20][21]中给出的方法进行计算，井底流压由动液面测试数据折算得到。

3.3 实际应用

文献[18]中理论模型实例:圆形油藏中心一口完善井，h=27m，φ=0.2，K=648mD，μo=3mPa·s，re=2000m，rw=0.1m，供给压力为9MPa，井底流压为8MPa。应用平面径向流公式计算Qo为319.6m3/d。将上述参数代入式(12)得到孔喉半径为:

根据验证公式(15)计算孔喉半径为:

二者基本一致，表明二维平面径向流孔喉半径计算方法是可靠的。

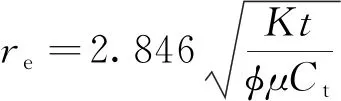
4 方法应用

利用笔者提出的基于产量、生产压差等动态资料的一维线性流动和二维平面径向流动下的孔喉半径计算方法对T油田18个区块进行开发效果评价。T油田属于复杂断块油藏，断块切割严重，断层密度大(2.3～5.6条/km2，平均3.0条/km2)；储层物性极差，为特低渗储层，渗透率在2.3～95.1mD，平均9.8mD，10mD以下储量比例达76.3%。

选定孔喉半径、孔隙度、可动流体百分数、原油黏度、拟启动压力梯度等5个因素，应用多元综合分类系数进行区块开发效果评价，其中孔喉半径、孔隙度、可动流体百分数与油田开发效果呈正相关关系，孔喉半径、孔隙度、可动流体百分数越大，开发效果越好；原油黏度、拟启动压力梯度与油田开发效果呈负相关关系，原油黏度、拟启动压力梯度越大，开发效果越差。孔喉半径应用笔者提出的公式(14)计算得到，可动流体百分数、拟启动压力梯度由室内实验结果回归公式预测得到。多元综合分类系数Feci计算公式为:

(16)

式中:Feci为多元综合分类系数，1；φmax为孔隙度最大值，1；rt,max为孔喉半径最大值，μm；pc为毛细管压力，MPa；Som为可动油饱和度，1；Som,max为可动油饱和度最大值，1；μo,max为原油黏度最大值，mPa·s；λ为拟启动压力梯度，MPa/m；λmax为拟启动压力梯度最大值，MPa/m。

根据每个区块的5个评价参数，应用式(16)计算得到多元综合分类系数(见表1)。以多元综合分类系数为横坐标，累计概率为纵坐标，绘制累计概率曲线，将大致有直线趋势的点连成一条直线。

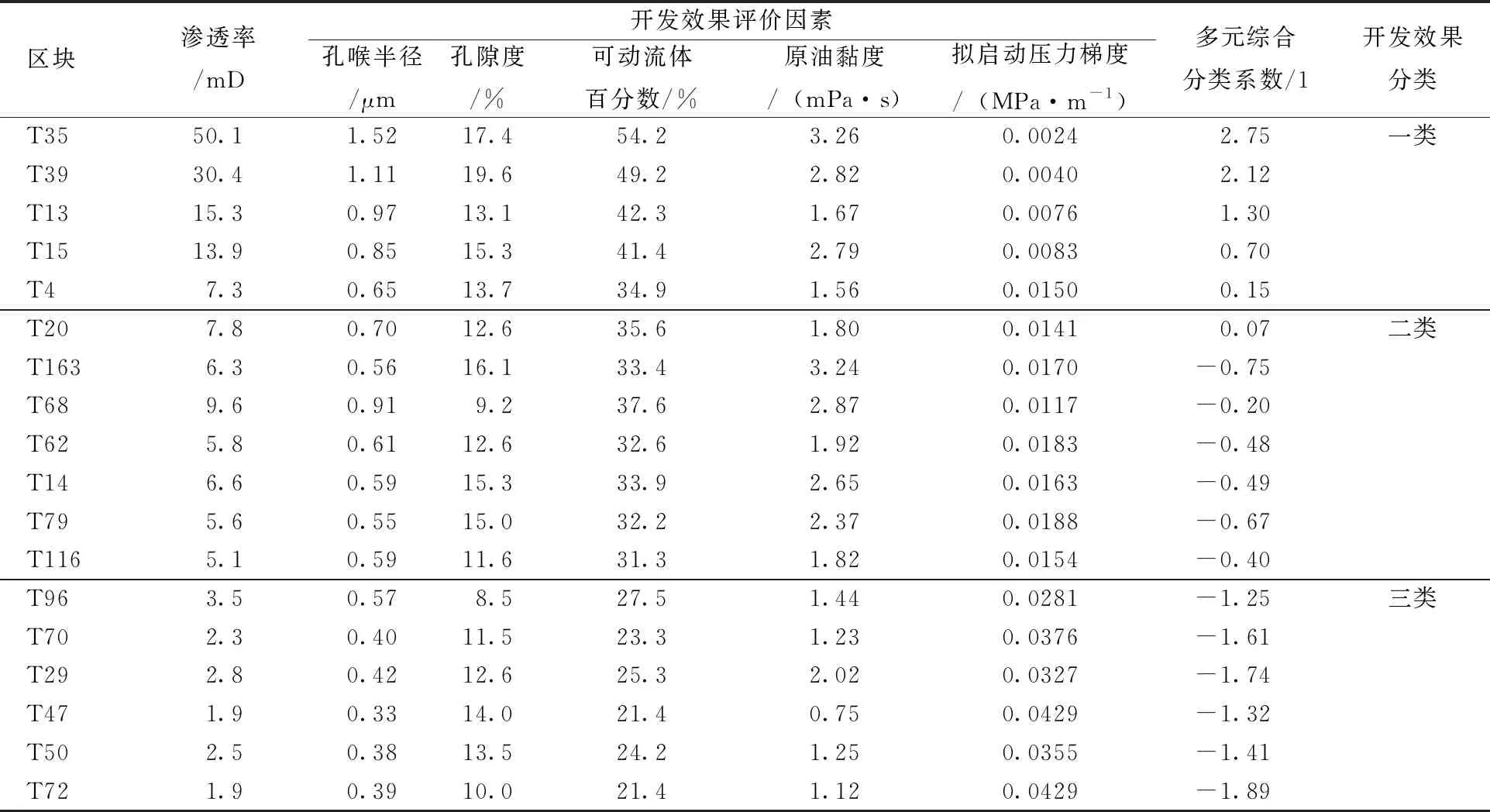
表1 T油田18个区块开发效果分类

从图3可以看出，累计概率曲线呈现3条直线。每一条直线为一个正态分布总体，代表一种类型开发效果，相邻2条直线的交点即为2类开发效果的分界点。3条相交的直线表明T油田18个区块开发效果可分为3类:一类区块5个，多元综合分类系数在0.15以上，储层物性较好，开发效果最好，初期单井产量高，在10t/d左右；二类区块7个，多元综合分类系数在-1.25～0.15之间，开发效果中等，初期单井产量在7t/d左右；三类区块6个，多元综合分类系数在-1.25以下，储层物性较差，初期单井产量在5t/d左右。

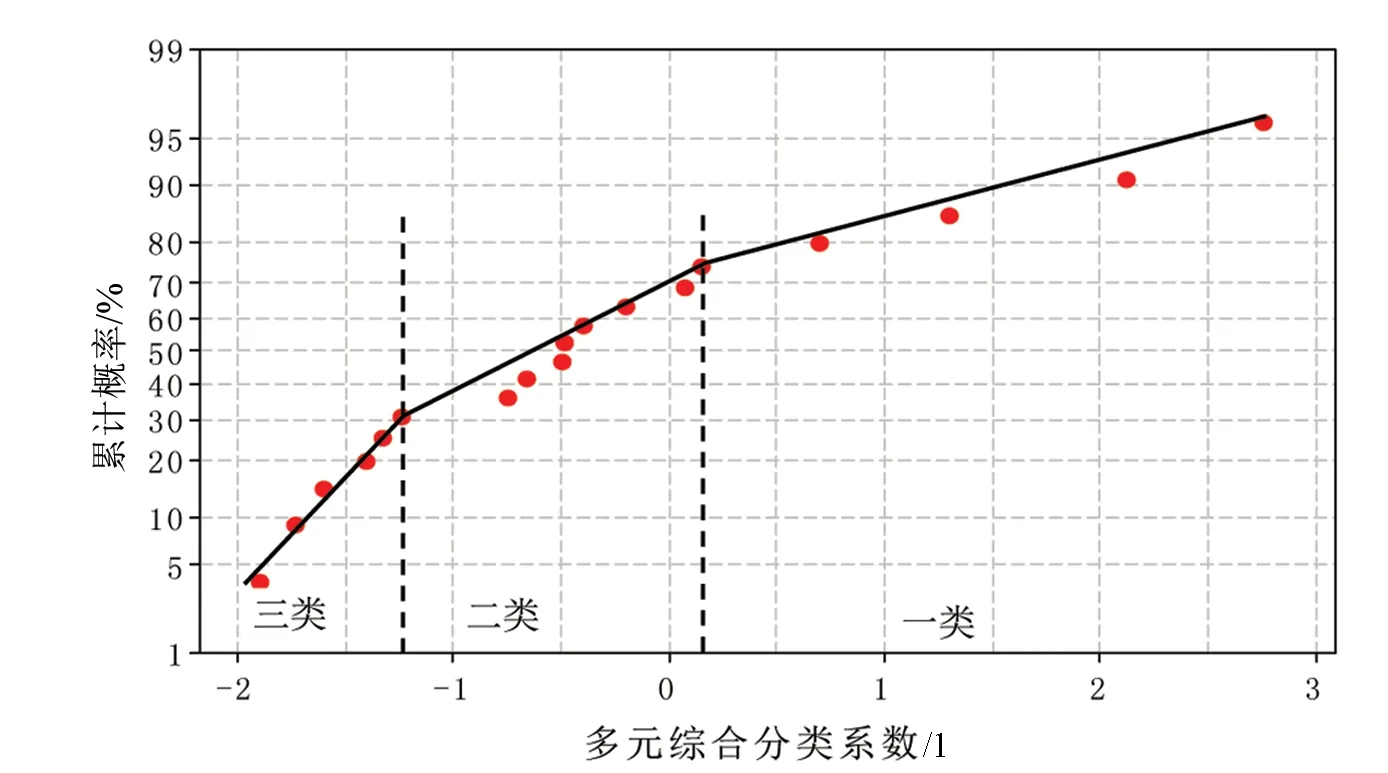
图3 T油田18个区块多元综合分类系数累计概率曲线Fig.3 Cumulative probability curve of multivariate comprehensive classification coefficient in 18 blocks of T Oilfield

对开发效果进行分类后，即可针对各区块开发中暴露的矛盾提出综合调整对策，改善开发效果。

5 结论

1)从毛细管束渗流模型、等效渗流阻力原理出发，首次从油藏开发动态角度建立了油层中常见的一维线性流动和二维平面径向流下的孔喉半径计算方法。该方法将油层有效厚度、产量等油田开发宏观参数和孔喉半径等储层微观参数联系起来，搭起了二者之间的桥梁。

2)依据等效渗流阻力原理，推导出根据孔隙度、渗透率、供油半径等参数计算的孔喉半径公式，验证了笔者提出的基于动态资料的孔喉半径计算方法的可靠性。

3)应用实例表明，笔者提出的孔喉半径计算方法是正确可行的，能够为微观孔隙结构分析、渗透率计算、区块开发效果评价提供反映地层流动特点的孔喉半径参数。