基于摄影测量获取边缘轮廓线的结构变形监测方法研究

姜 欣, 张晓艳, 唐 亮, 楚 玺

(重庆交通大学 土木工程学院，重庆 400074)

0 引言

桥梁挠度是评价整体结构性能的控制指标，对桥梁结构的挠度进行科学可靠的测试至关重要。传统的结构变形监测方法有水准仪人工测量、点式位移计直接测量、大地测量、GPS测量等，这些测量方法的不足之处在于只能获得结构局限关键点位的测量值，不能实现结构形态整体连续的变形监测。特别桥梁一类的大型结构物，需布设的测量点众多，现场测量工作十分繁杂，后期分析仍然面临测量数据不完备导致的结构损伤评价困难等问题。

数字图像处理技术(Digital Image Processing, DIP)是随着半导体集成电路技术和计算机科学技术的迅速发展而产生的—门新兴科学，是计算机图形学发展过程中极具里程碑式的成果。而近景摄影测量技术是数字图像处理技术的代表性分支，该技术的最大优势在于不接触被测量目标本身，便可获取被测物体大量的高精度几何信息，且测量过程经济、高效，是目前工程测量领域应用和研究的热点。王国辉[1]等使用手持相机和近景摄影测量技术对隧道洞室位移进行了测量，测量精度达到0.5 mm，满足隧道变形监测的工程应用需求。潘兵[2]等利用数字图像相关法(DIC)获得了亚像素条件下的土体位移测量，对算法精度与效率进行了比较，比较结果显示，摄影测量在精度上与常规土体变形监测精度一致，而测量效率提升45%。胡朝辉[3]等在数字图像处理的基础上，利用小波降噪，得到了较为理想的简支梁受载情况下的位移场。张国建[4]等首次利用近景测量技术实现了实桥的实时变形监测，但监测手段仍然依靠有限的测点，且需要在桥梁结构表面布设人工标记点。上述研究验证了数字图像技术在结构变形监测中应用的可行性，但应用领域仍然局限在小视域的结构形态测量和大型结构单点测量方面。

近年来，图像拼接技术的发展使得全息大视域结构形态监测成为可能。该技术可利用连续图像序列的重叠区域精密拼接出结构的大幅面全景图像，进而获取结构的全息形态。基于此，可首先对结构进行连续图像序列的采集，获得具备重叠区域的结构连续图像序列，进一步将连续图像序列的相邻图像在特征点的约束下进行精密拼接，形成高分辨率全息结构图像[5]。对于图像精密拼接最早可追溯到1965年的IFIP会议上，当时计算机图形学创始人Ivan Sutherland首次提出利用图像拼接的方法得到大视场的全景图像。周美丽[6]等提出以傅里叶变换为基础，从而将原始图像换置到频域区，对图像进行处理和平移后得到拼接图像的方法，这种方法称为相位相关法。崔栋[7]等提出了拓展相位相关法，对图像的旋转和缩放进行了优化。江铁[8]等提出了能够自适应的全景图像融合算法，这种算法使得图像拼接技术的发展突飞猛进。2008年，李柏林[9]等新提出基于RANSAC算法的图像配准方式，转换模型利用了二次导向提出的仿射矩阵进行仿射变换。2013年，何宾[10]等在现有的配准方法上改进出了F-SIFT图像拼接算法，这种算法的改进使得图像的配准在速度和精度上都有更优的表现。全景图像拼接技术虽然一直在优化和发展，但仍存在有以下问题: ① 使用多基线摄影测量则要求图像重叠度高，这给人员在实际测量应用上带来技术问题，即如何对各种桥梁结构进行相适应的拍摄方法，这是近景摄影测量走出实验室亟需解决的问题。② 传统多基线交向摄影方法繁多，所得影像多依赖于摄影人员的摄影知识。但手动控制摄影角度容易导致摄影对象的“摄影漏洞”，使得拍摄结果不理想。③ 实际桥梁结构地理位置与大小都会对摄影结果产生干扰。大型结构所需的摄影数量较多，很难对所得影像进行规范获取。基于此，本文提出一种针对桥梁结构的移轴线阵推扫摄影测量方法，该摄影测量方法的采样路径平行于桥梁的结构立面，通过相机平行移动过程中控制测量相机的拍摄参数，即可完成桥梁结构的连续图像序列采集。

1 试验概况

1.1 试验梁概况

本试验加载对象为钢桁混凝土组合梁，其中桥道板采用C50预制混凝土桥道板，纵向共7个节段拼装而成，共有2种长度规格，其中两端节段为长度1 080 mm，中间5个节段为长度1 000 mm。试验梁布置及外观见图1。

图1 试验梁布置及外观

1.2 数据采集

本次试验过程中，采用百分表对提取的结构挠度值进行精度验证。在试验梁每个节点下部布设百分表，将11个百分表布置于11根钢桁梁的节点板底部(如图2所示)，两端处布置百分表测量支座的刚体位移。在每个工况加载完成后进行试件连续图像序列的采集工作，测量相机在固定高度平行的位置对试验梁进行拍摄，摄影测量过程见图3。所使用的测量相机型号为Canon-EOS 5DSR，镜头采用Canon EF24-70 mm f/2.8LLⅡUSM。相机及镜头参数如下：像素数目为5 060万，像幅为8688 × 5 792，镜头型号为EF 24-70 mm f/2.8L Ⅱ，传感器尺寸为36 mm×24 mm，像素尺寸为4.14 μm，镜头相对孔径为F2.8～F22；数据接口为USB3.0，镜头接口为佳能EF卡扣，镜头焦距为24～70 mm，长宽比为3∶2，模组尺寸为152 × 116.4 × 76.4，最大直径及长度约88.5 mm×113 mm，感光原件为CMOS，产品重量约845 g，镜头重量约805 g。

图2 百分表布置

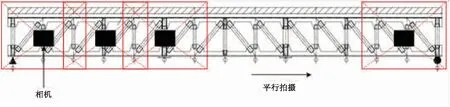
图3 摄影测量拍摄方法

1.3 加载方案

试验将在100、200、300、400 kN共4个荷载等级下进行。使用油压千斤顶进行试验加载，加载位置见图4。在进行加载时，均以20 kN为增量从0 kN分级缓慢加载至400 kN，每级加载后进行持荷2 min，而后对数据进行采集和保存。

图4 加载位置

2 基于尺度不变特征变换(SIFT)的图像精密拼接方法

连续图像序列同名点匹配是结构大幅面图像拼接的前提和关键，因此连续图像序列间的同名点匹配不仅要精度高、速度快,而且要非常稳健。结构立面表面的自然纹理特征能够构成天然的连续图像序列同名点。在相邻图像序列的重叠区域，结构表面的纹理特征具有一致性，只要摄影测量的精度够高，这些纹理特征就能够在图像的尺度空间内以极值点的形式被检测和表达。

目前在图像的尺度空间内寻找和检测极值点最常规的方法就是利用尺度不变特征变换(Scale-Invariant Feature Transform，SIFT)[11-14]，其基本思想是首先在多尺度空间中检测图像的特征点，并对特征点的尺度、位置和方向进行确定，然后对特征点生成特征向量描述符，最后实现特征点匹配。

本文将SIFT特征点的提取和配准分为以下2个步骤：①图像尺度空间的构造；②尺度空间特征点描述和配准。

2.1 图像尺度空间的构造

将原始图像与高斯核函数G(x,y,σ)进行卷积运算，建立多尺度空间L(x,y,σ)。

(1)

L(x,y,σ)=G(x,y,σ)×I(x,y)

(2)

式中:(x,y)为空间坐标；σ为可变尺度空间因子，其实质为高斯卷积模板矩阵的大小。以本文获取连续图像序列为例，不同的σ值可以将原始图像序列不断地降阶采样，得到不同大小的图像序列，由大到小，从下到上构成塔状模型，从而生成被处理图像序列I(x,y)的多尺度空间如图5所示。

图5 图像序列的多尺度空间

使用图5的高斯金字塔，将其每组中相邻的上下2层图像进行减运算，即为高斯差分图像，如图6所示。

图6 DoG尺度空间的构建

上述DoG空间的局部极值点组成了本文连续图像序列重叠部分的稳固特征，将DoG相邻2层的图像对比得到该特征的粗略定位。任一像素点与所有相邻点的图像和尺度域对比后，可得到DoG函数的极值点。图7可看出，检测点与同尺度、相邻尺度的共26个点比较。满足本文对极值点具有较强的鲁棒性、稳定性、尺度不变性的要求[15]。

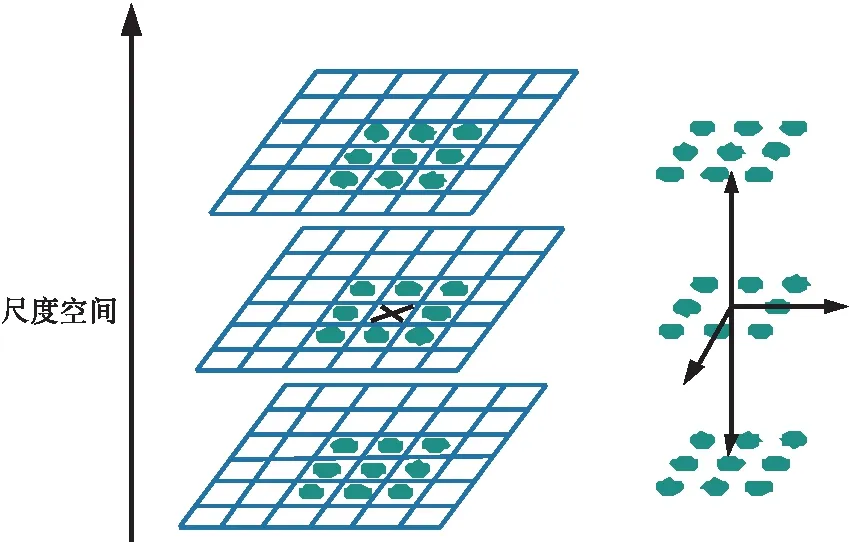
图7 DoG空间极值检测

2.2 尺度空间特征点描述和配准

由于图像局部的特征，可利用此特征将关键点设定基准方向。设定后的描述符附有旋转不变性。局部的稳定方向利用梯度求得。采集所有关键点在高斯金字塔中3σ邻域内的图像梯度和方向特征。像素梯度的模值和方向定义如下：

(3)

(4)

关键点的尺度空间值被定义为L。以特征点为中心，统计一定邻域内的像素点的梯度方向和梯度幅值，以梯度直方图来判定特征点方向。按照每柱10°，将360°的方向在梯度直方图中划分为36个柱，柱的长度即为像素点的梯度幅值，位置与角度即为梯度方向。如图8所示。在梯度直方图中，特征点处邻域梯度的主方向由最大峰值柱所在位置角度表示，也就是特征点的主方向；如果还有峰值柱为主峰的80%，则把这个峰值柱的位置角度作为此特征点的辅助方向。

图8 特征点主方向规定方式

根据上述步骤，任何一个关键点均有尺度信息、方向信息和位置信息。这3个信息能够成为相邻图像精密拼接的位置约束。

利用上述算法对本文获取的钢桁混凝土组合梁试件连续图像序列进行拼接。拼接结果如图9所示。

图9中，试验梁图像的像幅由原有像素大小8 688×5 792 pixel增大到43 440×5 792 pixel，像素分布密度在监测位置明显提高。针对桥梁这种“细长”结构，该摄影测量方法有效地增大了x方向的视场范围，从成像效果上初步验证了该方法在桥梁结构变形监测中应用的特殊针对性。

图9 试验梁全景拼接图像

3 结构边缘轮廓线提取

3.1 边缘检测

边缘是图像的重要组成部分，是图像处理主要特征提取手段。其实质在于通过算法对图像主体与背景之间灰度值变化剧烈的点进行提取，进而得到所需目标与背景的交界线[16]。对灰度求导，可得到边缘点的变化程度。

一维时，图像的阶跃边缘与其一阶导数部分峰值相联系。图像函数f(x,y)在点(x,y)的一阶微分G(x,y)是具有方向和大小信息的矢量：

(5)

可得，G(x,y)与函数f(x,y)增加时最大变化率方向相同。

一阶微分的幅值为：

(6)

一阶微分的幅值可用绝对值近似：

|G(x,y)|=|Gx|+|Gy|

(7)

或

|G(x,y)|≈max(|Gx|,|Gy|)

(8)

由分析知，一阶微分的方向定义为：

α(x,y)=arctan(Gy/Gx)

(9)

式中:α角是相对x轴的角度。

从而图像灰度的变化程度可用一阶微分的离散逼近函数来检测，增强图像中所需检测的区域，对一阶微分进行阈值运算，若所得值大于设限值，则存在边缘[17]。

以试验梁下边缘为对象进行提取(见图10)，可获得粗略的下边缘线形(见图11)。放大图11的轮廓线，在像素尺度分析结构轮廓线的像素排布可知受测量光场环境噪声的影响，提取的结构边缘轮廓具有局部不连续的性质，存在间断点，因此需要对这一问题进行修复得到相对完整的结构轮廓线。

图10 轮廓提取位置

图11 钢桁梁下缘粗略线形

3.2 不连续边缘检测算法对提取轮廓线型的改进

由于存在噪声，使得结构图像边缘断点不连续(见图12)，导致在对模糊图像进行处理时[18]，边缘检测失真，因此常规边缘检测算法很难对模糊图像的边缘进行准确地识别和定位。由图12可见，本文试件提取出的边缘存在明显不连续现象。

图12 局部放大图

本文提出一种改进检测算法对模糊图像的边缘进行提取，流程如图13所示。通过“广义交叉验证准则”[19]先对噪声进行强弱区分。当噪声判定为弱时，仅对图像进行模糊边缘检测算法；当噪声判定为强时，对图像进行模糊滤波和模糊边缘检测算法同时处理。

图13 图像不连续边缘检测算法改进流程图

3.3 灰度形态学的基本运算

粗略轮廓线边缘为不连续边缘，为了得到连续边缘需要对其进行灰度形态学的基本运算。图像的模糊不连续边缘主要有膨胀、腐蚀、开启和闭合共4种形态体现。产生原因是图像灰度值突变。在灰度图像中处理这4种形态为灰度形态学[20]。

将灰度图像用f(x,y)来描述，b(i,j)是结构元素，f和b的定义域用Df和Db来描述。4种形态如下式所述：

① 腐蚀定义：

(fΘb)(x,y)=

(10)

② 膨胀定义：

(f⊕b)(x,y)=

(11)

③ 开启运算定义：

f(x,y)·b(x,y)=[(fΘb)⊕b](x,y)

(12)

④ 闭合运算定义：

f(x,y)·b(x,y)=[(f⊕b)Θb](x,y)

(13)

3.4 提取结构轮廓线滤波

在粗略轮廓线上进行以上灰度学运算后得到修复后的结构边缘轮廓线，见图14。但由于以下2种原因，图14中所提取的结构边缘轮廓线有明显振荡效应。主要原因是结构边缘并非单一均匀像素构成。由图15中的深色像素块可知，其边缘可由多个像素组成。由于试验光场环境影响，使得图像噪声与真实边缘搅混一起，部分像素会产生并排排列状，真实边缘无法准确定位。需要由像素带宽的所有像素灰度值的梯度变化率精确定位。结构边缘像素点存在阶跃行为，无法使挠度曲线完全平滑。故所提取的结构边缘线与实际边缘仍有差别(如图15中实线和虚线所示)。

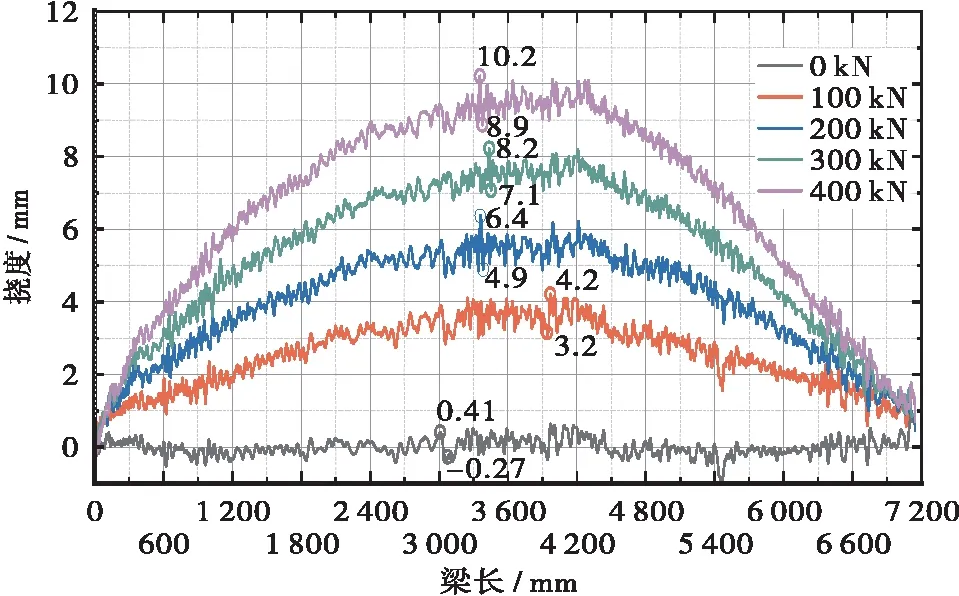
图14 结构边缘轮廓线提取

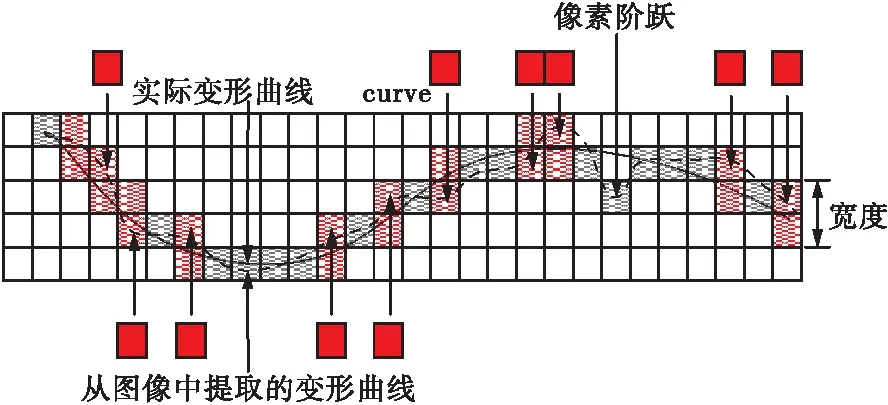
图15 结构边缘轮廓震荡的成因

为得到实际挠度曲线，对图14提取的轮廓线进行拟合处理，得到向实际形态挠度曲线逼近的边缘线性，如图16所示。

图16 提取的结构边缘轮廓线拟合

为了验证本文方法的精度，将图16所示的结构边缘轮廓线与初始工况即0KN时的结构边缘轮廓线进行叠差，得到试验梁的整体变形曲线，如图17所示的。结构整体变形挠度曲线与百分表对比如图18所示。

图17 与初始工况叠差分析获取的结构相对变形图

4 影像数据处理及结果分析

由图18可知，本文采用摄影测量所提取的结构整体挠度曲线与百分表数据一致。说明本文提出的结构边缘挠度曲线提取方法，符合常规变形测量方法拟合挠度曲线特征和实际变形规律。且相比常规单点变形测量，摄影测量提取的结构变形曲线能够更加完整地反映结构实际变形，包含信息更丰富。由整体变形测量精度对比如表1所示。

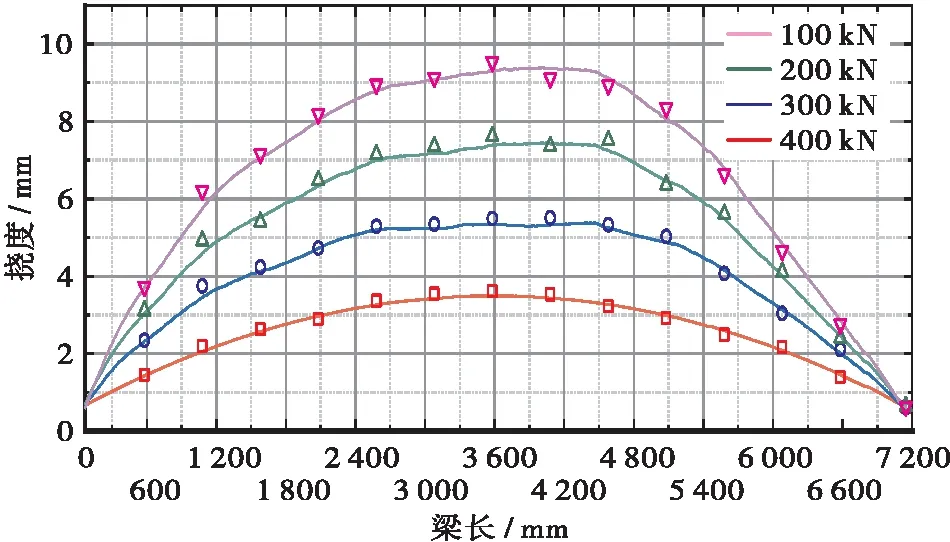
图18 摄影测量提取的完整挠度曲线与百分表对比图

由表1可知，获取的结构边缘变形测量精度平均误差为1.79%，最大误差为4.74%，满足桥梁结构变形监测的应用需求。

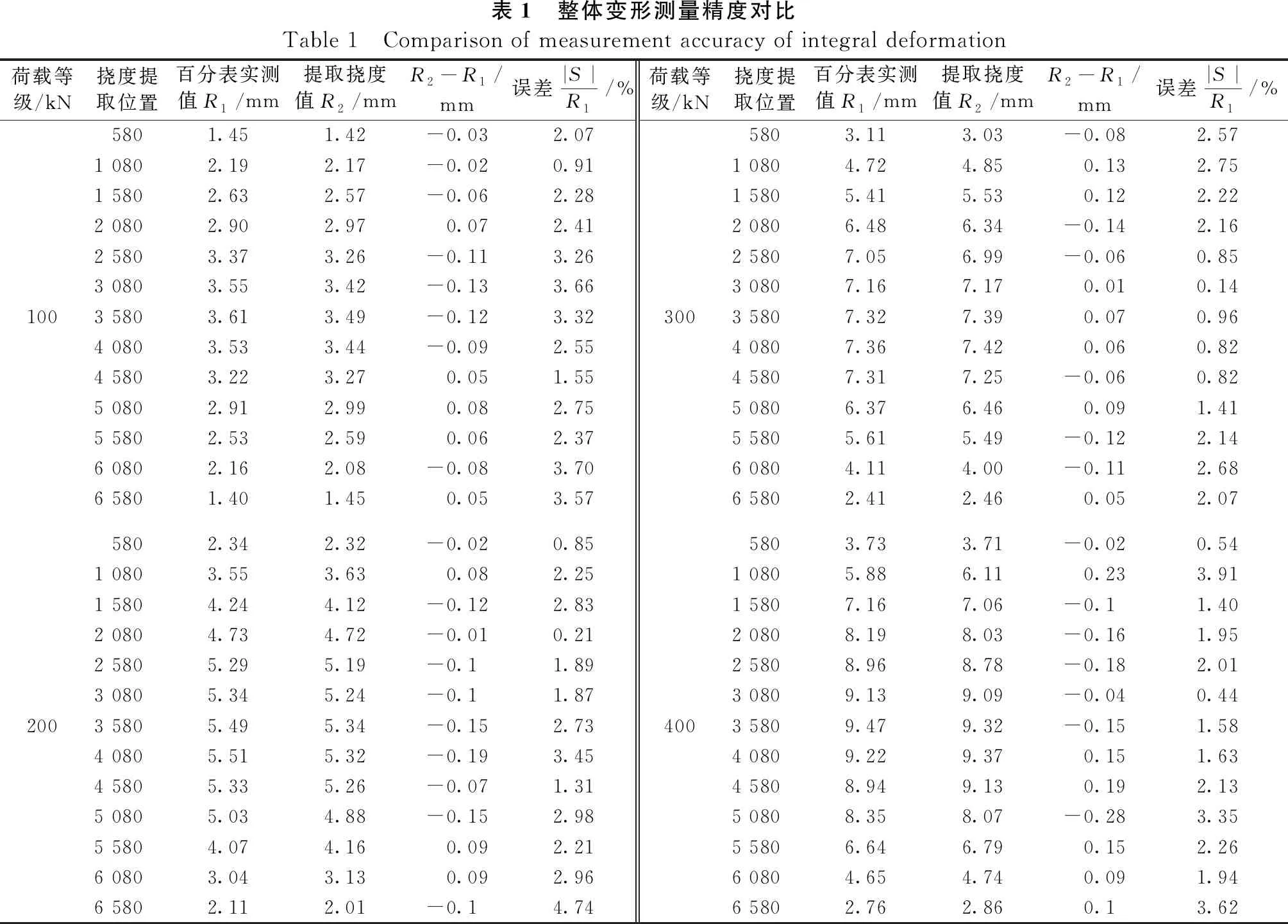
表1 整体变形测量精度对比Table 1 Comparison of measurement accuracy of integral deformation荷载等级/kN挠度提取位置百分表实测值R1/mm提取挠度值R2/mmR2-R1/mm误差|S|R1/%荷载等级/kN挠度提取位置百分表实测值R1/mm提取挠度值R2/mmR2-R1/mm误差|S|R1/%5801.451.42-0.032.075803.113.03-0.082.571 0802.192.17-0.020.911 0804.724.850.132.751 5802.632.57-0.062.281 5805.415.530.122.222 0802.902.970.072.412 0806.486.34-0.142.162 5803.373.26-0.113.262 5807.056.99-0.060.853 0803.553.42-0.133.663 0807.167.170.010.141003 5803.613.49-0.123.323003 5807.327.390.070.964 0803.533.44-0.092.554 0807.367.420.060.824 5803.223.270.051.554 5807.317.25-0.060.825 0802.912.990.082.755 0806.376.460.091.415 5802.532.590.062.375 5805.615.49-0.122.146 0802.162.08-0.083.706 0804.114.00-0.112.686 5801.401.450.053.576 5802.412.460.052.075802.342.32-0.020.855803.733.71-0.020.541 0803.553.630.082.251 0805.886.110.233.911 5804.244.12-0.122.831 5807.167.06-0.11.402 0804.734.72-0.010.212 0808.198.03-0.161.952 5805.295.19-0.11.892 5808.968.78-0.182.013 0805.345.24-0.11.873 0809.139.09-0.040.442003 5805.495.34-0.152.734003 5809.479.32-0.151.584 0805.515.32-0.193.454 0809.229.370.151.634 5805.335.26-0.071.314 5808.949.130.192.135 0805.034.88-0.152.985 0808.358.07-0.283.355 5804.074.160.092.215 5806.646.790.152.266 0803.043.130.092.966 0804.654.740.091.946 5802.112.01-0.14.746 5802.762.860.13.62

5 结论

本文针对结构挠度全息变形监测方法开展试验研究。所得结论如下：

a.采用SIFT算法对试件的连续图像序列进行了精密拼接，拼接结果显示移轴摄影测量方法能够在结构变形监测领域开展应用，监测结构物的像素和像幅均明显提升。

b.对试件拼接图像的轮廓线挠度进行提取，发现对受噪声影响存在结构边缘不连续的问题，进一步对含噪声的不连续边缘提出了一种边缘检测改进算法，通过灰度形态学膨胀和腐蚀运算实现了结构的连续轮廓线的断点回归。

c.研究发现受噪声影响，结构图像边缘存在振荡效应，采用多项式拟合完成了结构图像边缘向真实边缘的逼近。与百分表的实测挠度对比分析显示，提取的结构轮廓准确，边缘变形信息完整，最大挠度测量误差4.74%，平均误差为1.79%。