杨树防护林土壤蒸发及其影响因素
李 伦, 刘海军, 高壮壮, 杨 丽, 冯东雪
(北京师范大学 水科学研究院 城市水循环与海绵城市技术北京市重点实验室, 北京 100875)
杨树(Populusspp.)作为中国北方地区主要的人工林树种,被广泛用于公路、铁路防护林以及城市绿化等方面[1-3]。其生长对水、光、热等条件都具有较高的要求[4-5]。中国北方多为干旱、半干旱区,水资源短缺,蒸发作用强烈[2]。蒸发作为缺水地区耗水量的重要组成部分,直接影响着当地的水文循环、土壤水分的变化情况,也影响着杨树的正常生长发育[6-7],缺水地区杨树大面积种植的可持续性引起越来越多的关注。定量计算林间土壤蒸发量,研究土壤蒸发规律及其测量技术对于林间水分管理以及作物耗水规律的研究具有重要的意义。国内外许多学者从水文学、气象学等不同的角度,对土壤蒸发过程及其影响要素进行研究并建立了定量的计算方法。Fox[8]基于能量平衡方程,利用土壤与理想干土柱表面温差与日累计风速建立了土壤蒸发的估算公式;Ben-Asher等[9]对Fox的模型进行了改进,引入积分的概念,利用土表温差与风速建立了相对蒸发量的计算方法;Alvenas等[10]以土壤热流的计算公式为基础,建立了土面蒸发的估算公式;张建国等[11]分析了土壤蒸发与水面蒸发的关系,通过一维平差处理对防护林土壤蒸发进行估算;高壮壮等[12]利用不同水分条件下土壤表层温度的差异,建立了以饱和土壤为参考的不同水分条件下土壤蒸发量的估算公式。目前,对于土壤蒸发量的估算多数都是建立在理论模型的基础上,模型的准确性、适用性需要根据实际的应用条件进行调整和检验;模型计算时所需的参数较为复杂;模型的推广受到当地气候、下垫面等条件的影响。林下土壤蒸发不仅受到土壤本身条件的影响,同时受到林木覆盖等影响,以上公式直接利用会造成较大的误差。本试验以河北省邢台市大曹庄国家级种子试验站东侧道路两旁的杨树林为研究对象,利用微型蒸发器和20 cm蒸发皿对林下水面及土壤的实际蒸发量进行测量,分析防护林地的气候特征,以水面蒸发为参考,建立估算土壤蒸发量的公式,探求估算林下土壤蒸发量的简便方法。
1 材料与方法
1.1 研究区概况
试验于2019年8—10月在河北省邢台市宁晋县大曹庄国家级种子试验站(37°29′49.25″N,114°55′40.59″E,海拔26 m)进行。试验站东侧为406乡道,杨树防护林种植于公路两侧,单侧防护林宽15 m。研究区1981—2018年的年平均降水量在218~666 mm,多年平均降水量为430 mm,2019年降水量为499.6 mm;多年气温平均值为13.03 ℃,平均值日照时长为2 428 h,无霜期约250 d[1,13]。研究区地势平坦、土质肥沃。防护林地0—60 cm的土壤均为粉壤土(表1)。杨树树种为速生107杨(Popolus×euramericanacv. ‘Neva’ );树龄为10 a;平均树高为15.6 m;平均胸径17.3 cm;平均冠幅为2.25 m;防护林内杨树的株距约为3.0 m,行间距约为3.5 m;林区无灌溉条件,春秋季节进行修剪。

表1 研究区土壤性质
1.2 试验设计
1.2.1 蒸发量和温度测量 在防护林行间中心处布置3个20 cm蒸发皿和自制的6套微型蒸发器(micro-lysimeter, ML),测量水面的蒸发量及林下原状土的蒸发量。微型蒸发器由PVC管加工而成,其中内管高度为150 mm,壁厚为3 mm,内径为104 mm;外管内径为120 mm,固定于行间,方便取出和放回内筒,同时能够避免更换土壤时对土体的破坏[14-16]。用微型蒸发器取原状土样时,将内管垂直压入土中,带土整体挖出后用保鲜膜封底,用皮筋及胶带固定。每日上午7:00用精度为0.01 g的电子天平测量蒸发皿及微型蒸发器的质量,3个蒸发皿与其前1日的质量之差的均值为前1日的林下水面蒸发量,6套微型蒸发器与前一日的质量之差的均值为前1日的土壤蒸发量。为了保证试验的精度,每次测量后,将20 cm蒸发皿内的水补充到深度为20 mm,并测量蒸发皿质量,每2 d更换微型蒸发器中的土壤,雨后要更换微型蒸发器中的土壤[17-18]。
土壤表层温度数据及蒸发皿内水体的温度采用TT-T-24型热电偶进行测量。在蒸发皿水面下约10 mm处布置3根温度传感器,在每个微型蒸发器内土壤表层5—10 mm处埋设3根温度传感器,采集器为CR1000(campbell scientifics, USA),采集频率为10 s一次,记录5 min的平均值。
1.2.2 气象数据的采集 气象数据使用试验站自动气象站进行采集,包括温度、辐射、风速、降水等,采集器为CR1000x(campbell scientifics, USA),采集频率为10 s一次,记录10 min的平均值。由于饱和水汽压差(VPD)与蒸发关系紧密,计算了日均VPD,计算公式为[1]:
(1)
式中:VPD为日均饱和水汽压差(kPa);Hr为日均相对湿度(%);t为日均气温(℃)。
1.3 数据处理
1.3.1 林下土壤相对蒸发量(RE) 水面蒸发量反映了试验环境下大气的蒸发能力。为了消除每日蒸发能力变化的影响,计算了土壤相对蒸发量RE(relative soil evaporation),其值为时段内林地土壤蒸发量与水面蒸发量的比值,即:
(2)
式中:Ea为林地土壤日蒸发量(mm);E0为日水面蒸发量(mm)。
1.3.2 林下土壤与水面温度差相对值(RT) 土壤蒸发会影响表层温度,因此基于土壤表层温度的变化来估算土壤蒸发量。将某一时段内的林地土壤表层温度与该时段内水的温度相减,得到该时段内土壤与水的温度差值ΔT。为了消除绝对温度的影响,采用温度差的相对值,计算公式为温度差除以该时段上水的平均温度。
(3)
(4)

1.3.3 干扰性数据筛选 本试验为露天试验,降雨会对试验结果造成影响,数据分析时剔除了9月9—13日及10月4日降水量较大日期的数据(图1),除此之外还剔除了仪器出现故障的9月20—25日的数据。

图1 试验期间降雨及风速的变化过程
1.3.4 数据分析 试验数据采用Microsoft Excel 2019和Origin 2021软件进行处理、作图和曲线拟合,利用SPSS 25.0对各气象要素与蒸发量进行相关性分析。为了评估所建立的模型的精度,采用均方根误差(RMSE)、平均相对误差(MRE)和纳什效率系数(NSE)进行评估[19]。
(5)
(6)
(7)
式中:Pi为第i个拟合值;Oi为第i个实测值;Oave为实测平均值;n为拟合值或实测值个数。
2 结果与分析
2.1 林下土壤和水面蒸发量及温度的日变化过程
图2为试验期间林下土壤及水面的日蒸发量和两者日均温度随时间的变化曲线。由图2可知,试验期间防护林内土壤及水面总的蒸发量分别为31.37和87.84 mm。和土壤蒸发相比,水面的日蒸发量变化更为剧烈,最大蒸发量为4.21 mm/d,日最小值不足0.5 mm/d;而土壤的日蒸发量较为稳定,在1 mm/d左右波动。土壤和水面温度在试验期间变化趋势一致,随着时间推移,温度呈现逐渐降低的趋势。
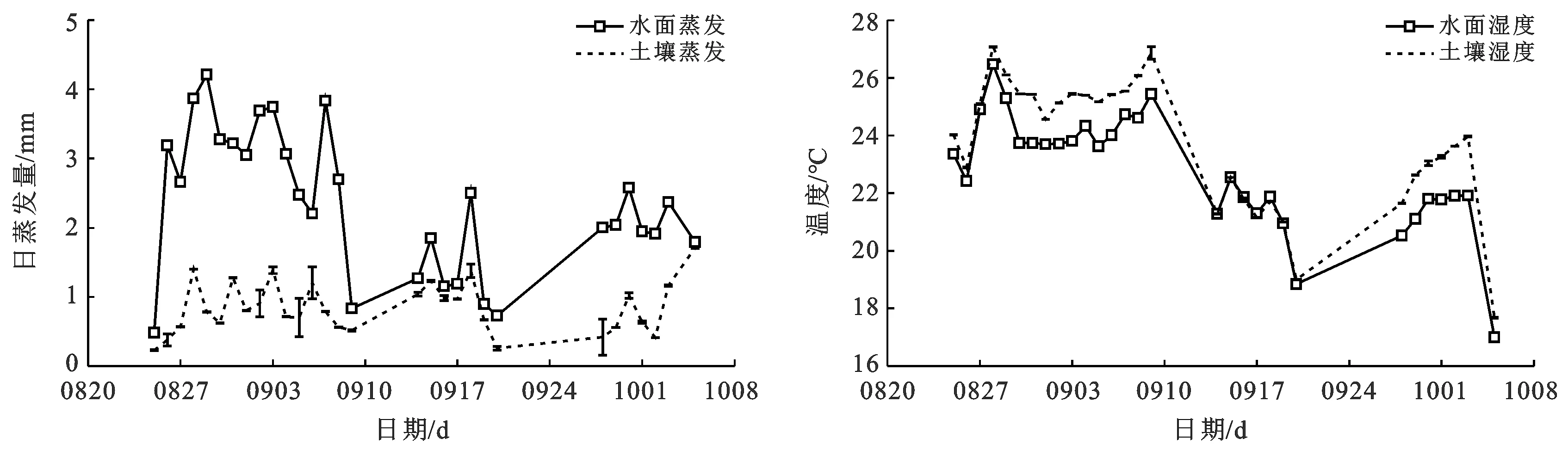
图2 试验期间土壤、水面的日蒸发量及日均温度的变化过程
2.2 蒸发量与气象要素的关系
对气象要素与林下土壤及水面的日蒸发量分别进行相关性分析,结果详见表2。由表2可以看出,林下水面蒸发与日总辐射及当日最高气温均呈现极为显著的正相关关系,相关系数分别为0.761,0.575;水面蒸发与日均气温呈现出较为显著的正相关关系,相关系数为0.373;土壤蒸发仅与日总辐射存在显著的相关关系,相关系数为0.331。辐射和空气温度为热力因子,为蒸发过程提供能量,可以通过控制水体能量的变化来影响蒸发。试验期间的土壤及水面的蒸发量与日均风速的相关关系均不显著。风速为动力因子,主要通过影响水汽分子的扩散速度影响蒸发,日均风速较低时,蒸发量受风速影响较小,但是当日均风速较大时,两者的蒸发量有明显提高(如8月29日、9月15日和9月30日)。水面蒸发与日均饱和水汽压差呈现显著的正相关关系,与日均相对湿度呈现显著的负相关关系,相关系数分别为0.579和-0.397,土壤蒸发与两者相关关系不显著。空气湿度和饱和水汽压差为水分因子,可以通过影响大气及物体表面的水汽压差来影响蒸发。

表2 气象要素与土壤及水面蒸发量相关分析结果
2.3 相对蒸发量RE与温度差相对值RT的关系
充分供水条件下,水体的温度主要受到气象条件的影响。但是当土壤中的水分逐渐消耗、含水量逐渐下降时,土壤蒸发量也逐渐下降,这时由于蒸发量的下降造成土壤温度比充分供水条件下的温度高,土壤蒸发条件下的温度和充分供水条件下的温度差与土壤蒸发量是相关的。为了寻求能最大程度反映土壤蒸发量的温度差,本研究分别分析了8月25日至10月7日数据测量期间数据较好的26 d的日均相对温度、白天8:00—18:00,10:00—16:00时与12:00—14:00平均相对温度差值RT与日相对蒸发量RE的关系(见图3)。由图3可以看出,基于拟合公式的决定系数(R2),12:00—14:00时平均的RT与日相对蒸发量RE拟合效果(图3)要优于其他时段。
2.4 土壤蒸发量公式拟合与验证
从图3可以看出,利用12:00—14:00时的平均温度差相对值RT与日相对蒸发量RE所建立的关系估算土壤蒸发量的效果最好(回归公式的决定系数R2最大)。但是对于图中建立的三次函数,随着RT的继续增大,RE会逐渐降低,甚至会出现小于0的情况,与实际不符。由图3可知,开始时随着RT的增大,RE快速减小,当RT大于某一值时,RE逐渐趋近于一个常数,因此本文用分段函数拟合。为了满足模型建立和验证使用的数据相互独立,选择将试验期间的蒸发及温度数据分为A组(9月14日至10月5日,共14日)和B组(8月25日至9月9日,共12日)其中A组数据用于关系拟合,B组数据用于所建立关系的验证。利用A组数据拟合的公式如式(8),拟合曲线如图4所示,利用B组数据验证结果如图4所示,模型检验指标RMSE,MRE和NSE详见表3。

表3 A,B组数据的模型检验指标

图3 日相对蒸发量RE与日不同时间段平均相对温度差值RT的关系

图4 日相对土壤蒸发量(RE)和温度差相对值(RT)的拟合曲线(A组)及曲线验证(B组)
(8)
式中:RE为日土壤相对蒸发量; RT为日12:00—14:00平均温度差相对值。
通过A组数据建模和B组数据验证的结果看出,实测和估算的日相对蒸发量RE的R2均达到了0.9,RMSE分别为0.087,0.043,MRE的绝对值小于10%,NSE均大于0.9,表明该拟合公式可用于计算试验区林下土壤蒸发量。
3 讨 论

土壤蒸发对土壤温度的影响使得利用土壤温度变化估算土壤蒸发成为可能。马已安等[6]以一次供水的不同表面条件的土壤与水面进行对比,将裸地的蒸发过程划分为3个阶段,将压砂地土壤蒸发划分为2个阶段。高壮壮等[12]以一次供水与充分供水条件下的土壤蒸发为研究对象,发现两者的温度差相对值随着蒸发过程的进行逐渐增大,当蒸发进行到水汽扩散阶段时,温度差相对值趋于稳定。本试验中,基于温度差变化将RE变化过程分为了两个阶段。在第一阶段,初始时,土壤含水量相对较高,土壤水分供水相对充足,蒸发对土壤温度影响小,土壤与水面温度差值不大,RT接近于0;随后土壤含水量的降低,蒸发所利用的辐射能量逐渐减少,部分辐射能量转化为感热通量提高了温度,这时RT逐渐增加,RE也逐渐减小;当RT>0.11后, RE趋近常数0.164,此时土壤中的液态水分含量极低,土壤蒸发进入到水汽扩散阶段,土壤温度已不受土壤含水量的影响,而主要受辐射的影响[28]。
使用微型蒸发器进行土壤蒸发测定简单实用,但是在应用过程中仍然面临着一些问题亟待解决。微型蒸发器无法测定植物根系吸收水分造成的土壤水分变化的过程[29],未来可进一步结合植物蒸腾耗水进行研究,整体分析杨树防护林蒸散发过程。不同土壤质地条件下,土壤含沙量,土壤孔隙、热容量等性质的不同会改变土壤水分的运动特征进而影响土壤表层温度及蒸发量[6,12,26],本文仅研究了粉壤土条件下的防护林土壤蒸发,条件比较单一,今后可改变土壤质地,研究其对蒸发的影响。含水量是影响土壤蒸发的重要条件,不少学者从含水量的角度研究了蒸发量与含水量间的变化规律[2,6,20-21,26]。本文主要尝试利用水面及土表温度差相对值来建立估算土壤蒸发量的经验公式,但是土壤含水量的测定对土壤蒸发规律的研究以及划分蒸发阶段有十分重要的意义,在今后的土壤蒸发量估算的研究中,将ML内的土壤含水量纳入测定范围。
4 结 论
(1) 林下影响水面蒸发的气象因素排序为辐射、饱和水汽压差和温度;但是林下土壤含水量总体较低,使得土壤蒸发与气象要素关系较弱。
(2) 林下土壤相对蒸发量RE随土壤与水体温度差相对值RT变化过程可以分为两个阶段:RE随RT的增加逐渐减小,当RT大于0.11时,RE趋近于常数0.164,认为此时蒸发过程已经进入到水汽扩散阶段。
(3) 构建了基于土壤—水体温差的土壤蒸发量公式,经验证估算的土壤蒸发量与实测的土壤蒸发量接近(R2=0.9),因此本研究提出的方法为原位测量并估算林下土壤蒸发提供了新思路。

