基于粒子群算法的行星齿轮传动设计与优化

伊成山，赵天真

（1.青海民族大学，西宁810000；2.浙江工业大学，杭州310014）

自1995年Kenney和Eberhard提出了粒子群优化算法（particle swarm optimization，PSO）[1]以来，相关专家学者们就开始对该算法展开深入的研究。

1 粒子群优化算法

粒子群优化算法是目前多数进化约束算法的一种，其基本原理就是一种随机的搜索算法。粒子群优化算法不局限于问题的具体领域，且其有比较大的收敛速度并能寻找全局最优，因此它在各领域应用十分广泛，例如在机器人的智能控制、工程设计问题、电力系统领域和交通运输等多方面学科领域。

PSO算法的特点具体如下：

1）PSO算法的构成要素较简单，主要由粒子群编码方法、个体适应度值和参数运行。

2）PSO算法不需要调节太多的参数，仅仅几个参数就可以对算法流程和结果产生直接的影响。

3）PSO算法比进化算法有更高效的并行搜索算法，计算速度更快，优化程度更高。

1.1 粒子群优化算法原理

通过自然界生物行为的基本特征，根据简单普遍的生存规则，利用先进的计算机网络技术将一些普遍的规则和特征转换为计算机语言，用模拟生物个体行为的方法解决众多应用领域的复杂过程。

在基本的粒子优化群算法中，每一个最优值的可能解都由一个粒子表示，所有的粒子在一起则会组成一个像鸟类集群似的群体。然后粒子会根据不断更新的群体信息和自身历史信息在整个解空间中改变其“飞翔”的方向及速度，在解空间中粒子会追随当前的最优粒子[2]，以此寻找最优解。

粒子群优化算法的初始种群就是一群随机粒子，这些随机粒子也被称为随机解，随机解经过速度和位置的反复迭代最终则会求得最优解。每一次迭代的过程中，每个粒子都会通过跟踪两个极值来不断地更新自己。两个极值分别是粒子自身历史最优解即个体解，整个种群历史最优解即全局极值[3]。粒子群优化算法流程如图1所示。

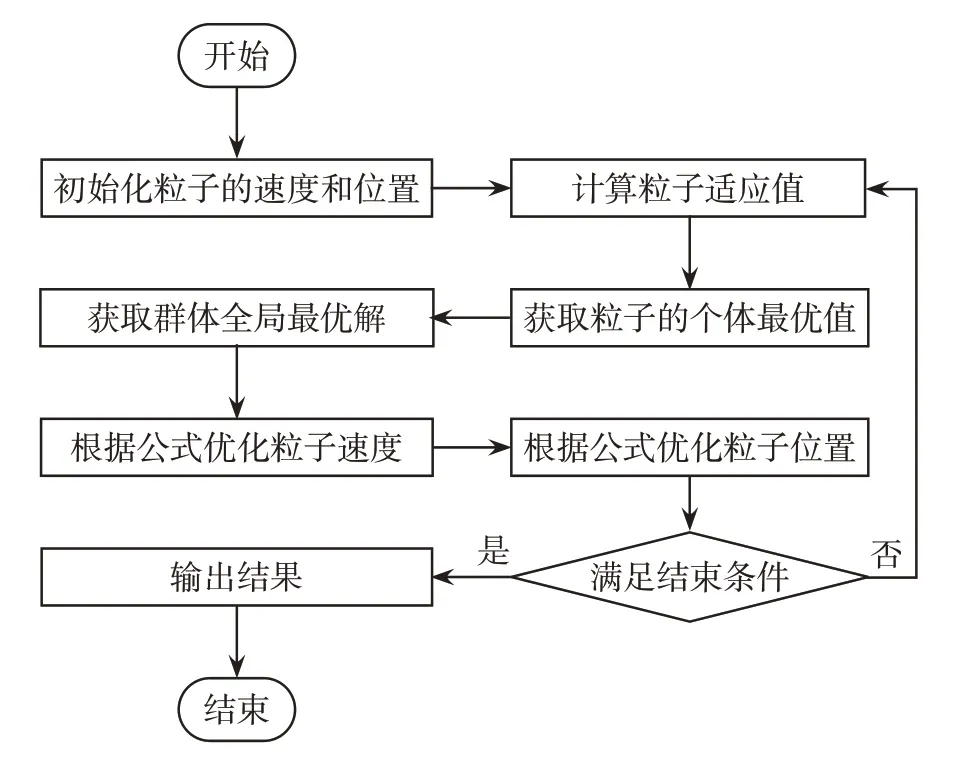
图1 粒子群优化算法流程Fig.1 Flow chart of particleswarm optimization algorithm

1.2 粒子群优化算法的数学描述

假设由N个粒子所组成的一个群落在一个D维目标搜索空间中。

1）在一个D维参数的搜索空间中，某个粒子在整个解空间的位置。

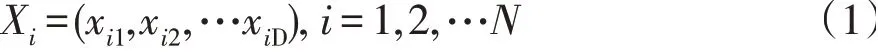
2）在一个D维参数的搜索空间中，某个粒子在整个解空间的速度。

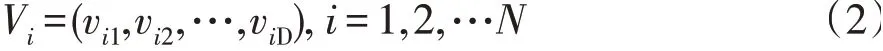
3）某个粒子为搜索到的自身历史最优值。

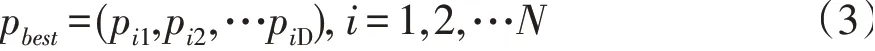
4）整个粒子群搜索到的种群历史最优位置。

5）在所有粒子找到两个最优值时粒子通过更新公式来比较历史值从而不断地更新自己的速度和位置。

式中，c1、c2为学习因子，取c1=c2=2；r1、r2为[0，1]之间的均匀随机数；ω是惯性权重因子，取ω=0.8[4]。在上式粒子速度更新公式中包含了3个部分：

（1）ω*vid惯性部分：即粒子当前的运动速度和将运动的趋势。

（2）c1r1(pid-xid)认知部分：即粒子在迭代的过程中对自己所经历的历史经验，并表示不断地向自己历史最优值靠近。

（3）c2r2(pgd-xid)社会部分：即粒子群中所有粒子在群体共同合作下寻找的群体历史经验，不断向群体或领域历史经验最优值靠近。

1.3 基本粒子群优化算法参数设计

不需要调节过多的参数是粒子群优化算法中最突出的一个优点，关键性参数主要有学习因子c1和c2、群体规模m和微粒子维数l、最大速度vmax、惯性权重因子ω，虽然参数不多但有些参数对算法的性能和收敛性有着关键性的影响。据相关研究经验参数设计如下：

1）学习因子c1、c2即加速常数：是调节粒子自身记忆和群体中其他同伴之间记忆的影响系数，可以很大程度地减少搜索时间。c1和c2根据相关参考文献[5]的实验研究表明通常取固定值c1=c2=2。

2）群体规模m和微粒子维数l：本课题所需解决的问题不会太过复杂，一般来说群体规模选取50即可。维数就是每个微粒的长度，其取值由具体优化问题而决定。

3）最大速度vmax：最大速度选取影响着微粒单步移动的最大距离，若最大速度过大，单步移动距离也会过大则会错过最优解，如若过小则会陷入局部最优。通常设定vmax=k·xmax，0.1≤k≤1。

4）惯性权重因子ω：惯性权重因子用来保持运动惯性，即可控制粒子当前的速度对下一步速度的影响。适当的权重因子可以在相对的迭代次数下获得全局最优解。经早期实验研究一般取ω在[0.80～1.20]之间会有较好的搜索能力。

2 行星齿轮传动设计

本课题的行星齿轮给定已知条件为，输入功率P=5 kW，输入转速n1=400 r/min，传动比ip=8，行星轮个数np=3，使用寿命为8年，每天平均工作12 h。根据齿轮的初始工况条件，选取适当的齿轮材料、热处理方式等。本次优化设计只针对齿轮传动部件进行优化，其他部件比如行星架、行星轮轴和轴承等选用将结合本次优化结果进行，本文中未涉及。行星齿轮传动各齿轮材料和热处理方式如表1所示。

表1 行星齿轮传动各齿轮材料和热处理方式Tab.1 Gear material and heat treatment for planetary gear transmission

按照国标标准对NGW型行星齿轮进行设计与计算，并对相关强度进行校核，齿轮传动啮合参数如表2所示，各齿轮主要参数如表3所示，各齿轮副啮合应力如表4所示。

表2 齿轮传动啮合参数Tab.2 -3Gear transmission meshing parameters

表3 各齿轮主要参数Tab.3 Main gear parameters

表4 各齿轮副啮合应力Tab.4 Complex stress of each gear pair

3 建立行星齿轮优化模型

把行星齿轮传动机构里的太阳轮齿数Za、行星轮齿数Zg、齿宽b和模数m作为设计变量，通过追求齿数优化以减小行星齿轮体积，且优化后的齿数需满足各项约束条件，不能一味地追求小体积，所以设计变量如下：

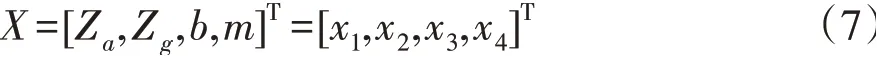
3.1 目标函数

在选定设计变量之后，根据设计变量的取值变化求取行星齿轮传动机构的体积最小，不仅要易于安装、节省材料以及降低生产的成本，还要考虑行星齿轮放入后体积会影响其传动时承受的载荷能力，同时又与结构几何参数以及啮合参数有关，综合考虑选择行星轮和太阳轮的体积为最终优化设计的目标函数。

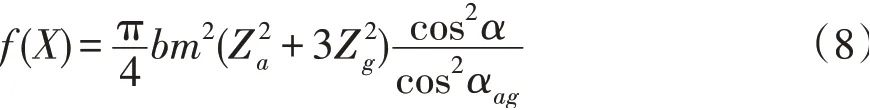
式中，αag代表外啮合角。

3.2 优化设计的约束条件

1）邻接条件。为让相邻的两个行星轮在与太阳轮啮合时不会产生碰撞，两行星齿轮中心之间的距离L大于行星齿轮齿顶圆的直径d，L＞dag，为a-g啮合副中心距。

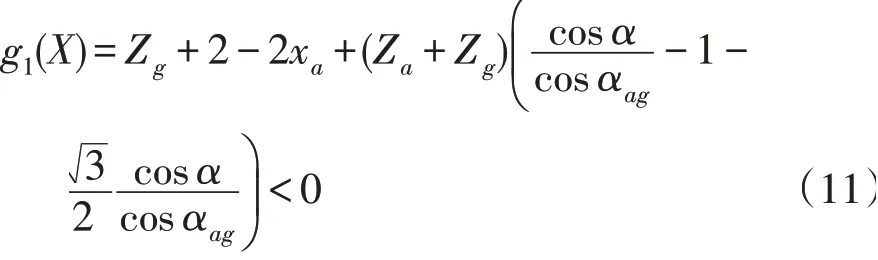
2）变位系数约束条件。在行星齿轮传动中，内外啮合变位系数和需要控制在一定的范围之内。当变位系数太低时齿轮的承载能力会降低，当变位系数太高时齿轮的重合度会降低，从而影响啮合效率。依据齿数比可确定变位系数的范围为：

3）太阳轮齿数约束条件为：

4）齿宽系数约束条件。齿宽系数为齿宽和直径的比值，一般在0.50～0.70中选取。其约束条件为：

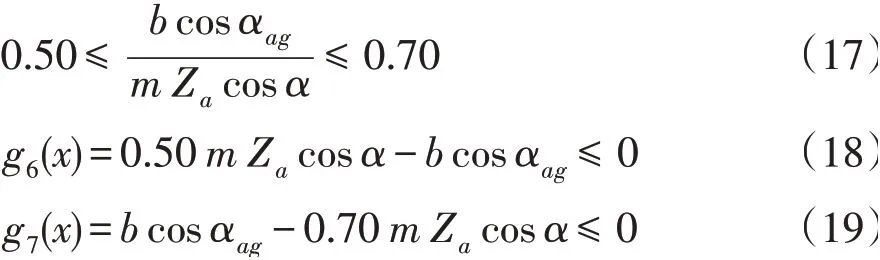
5）齿面接触疲劳强度条件为：

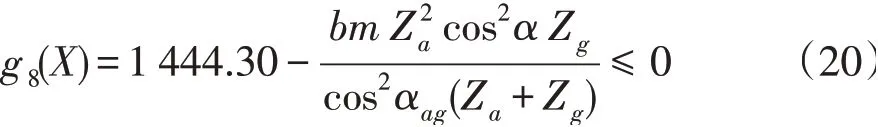
6）齿根弯曲疲劳强度条件。太阳轮的齿根弯曲疲劳强度条件为：

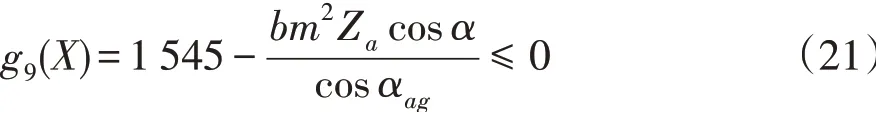
行星轮的齿根弯曲疲劳强度条件为：

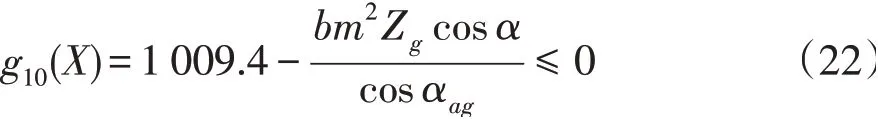
4 编程求解

采用粒子群优化算法，基于MATLAB编程对初始设计的行星齿轮体积进行优化求解。PSO算法优化太阳轮与行星轮相关参数进行优化减小行星轮体积，且优化后的参数和结果满足上述所有约束条件。

5 结果分析

把传统方法设计值、序列二次规划算法的优化结果与粒子群优化算法优化结果进行对比分析，优化结果对比如表5所示。

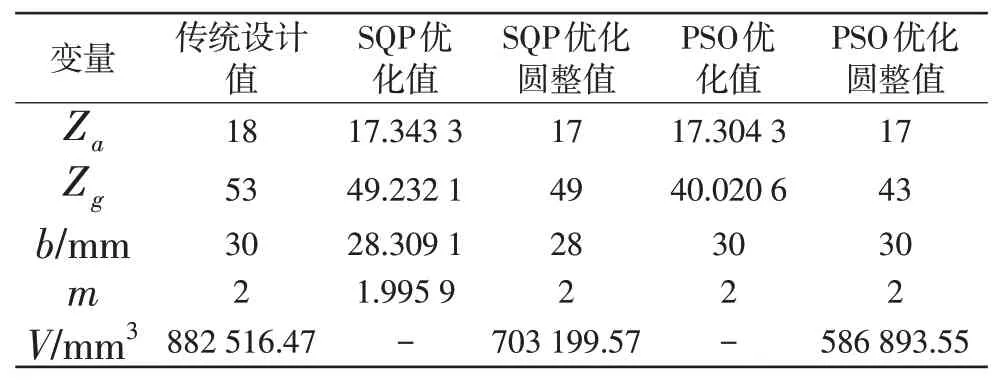
表5 优化结果对比Tab.5 Comparison of optimization results

根据国标标准，将优化值进行圆整取值后，可知采用粒子群优化算法可以提高设计效率，具有明显的优越性。

6 结论

本课题主要根据对传统设计方法设计的行星齿轮相关参数进行粒子群优化算法的计算。将体积问题抽象为数学模型，确定设计变量和约束条件，在优化过程中加入序列二次优化算法与粒子群优化算法优化结果对比，两种方法的设计算法皆基于MATLAB编程进行。由优化对比结果可知，采用粒子群算法对行星齿轮设计的优化效率最为显著。