基于遗传算法优化的电弧增材再制造焊道尺寸预测模型
倪永谦,王猛,杜心伟,刘仁培,魏艳红
(南京航空航天大学,南京 210000)
0 前言
电弧增材再制造技术是基于电弧增材制造技术,通过层层堆积的制造方式,实现零部件损伤部位的尺寸恢复和零部件性能恢复或提升的先进制造技术,具有制造成本低、修复效率高、零件性能好、材料利用率高等优点[1-2]。电弧增材再制造技术在航空航天、能源化工、轨道交通等高端技术装备领域具有广阔的应用前景。
成形件精度较低是制约电弧增材再制造技术发展的重要因素,保证成形效率的同时提高成形件精度是当下主要研究方向之一[3-5]。单道焊缝成形尺寸精度的控制对于增材再制造构件的成型精度具有重要影响,国内外学者对焊接参数和焊缝尺寸之间的模型关系也做了大量研究工作,Tao等人[6]开发了一种二阶回归模型来定量估计工艺变量对焊道几何形状的影响;Xiong等人[7]比较了人工神经网络(ANN)和二阶回归模型在4个焊接工艺变量下预测焊缝高度和宽度的准确性;Nagesh等人[8]建立了一个反向传播神经网络(BPNN)模型,该模型实现了输入因素(送丝速度、电弧功率、电弧电压、焊接电流、电弧长度和焊接速度)和输出因素(焊道高度、焊道宽度、焊道深度和焊道面积)之间的较高精度预测。
目前,已经证明人工神经网络在预测焊道几何尺寸方面有较高的预测精度和较强的泛用性[9]。然而,神经网络模型的结构及初始权值和阈值的选择会对网络训练精度产生较大影响,易出现局部最优解情况,降低模型精度。因此,文中采用遗传算法优化神经网络的方法对焊接工艺参数和焊道尺寸进行建模,实现依据焊接工艺参数对焊道尺寸的预测,提高模型的可靠性。
1 试验设备及方法
电弧增材再制造成形系统系统由GP12_AR1440工业机器人、机器人控制柜、焊接电源、送丝机构、冷却水箱、焊枪及工作台等部件组成。试验基板为Q235B钢板,尺寸为300 mm×200 mm×20 mm。焊丝为牌号RMD535模具修复专用药芯焊丝,直径1.6 mm,保护气体成分为80%Ar + 20%CO2,流量为15 L/min。
试验开始前,对基板表面进行机械打磨去除表面氧化层等杂质,随后用酒精清洁基板表面并风干处理对基板表面进行机械打磨,并用酒精清洗干净,然后将基板固定在工作台上,并设定好机器人焊枪运动轨迹及焊接工艺参数,进行试验。
电弧增材再制造成形过程的主要影响因素较多,包括电弧电压、焊接电流、送丝速度、焊接速度、焊丝伸出长度及保护气体流量等,各个因素之间存在高度的非线性耦合作用。其中,电弧电压、焊接电流、送丝速度和焊接速度对焊道的熔宽和余高影响较大,因此文中选取电弧电压、送丝速度和焊接速度3个焊接工艺参数为因素,在每个因素中选取5个水平值,选用L25(53)的正交试验设计方案,见表1,获得不同试验方案下的焊缝几何尺寸特征。
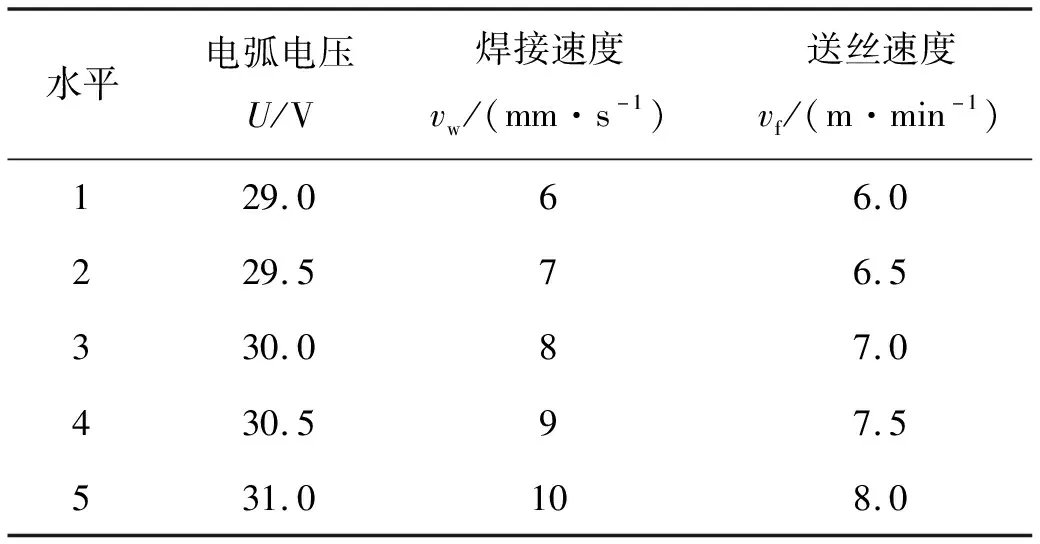
表1 工艺参数水平值
图1为单道成形外观形貌,表面呈现鱼鳞状,焊道宽高变化均较小。

图1 单道焊缝形貌图
试验结束后,对焊道熔宽W和余高H进行测量,如图2所示。用游标卡尺测量不同的焊接工艺参数对应的焊道高度与宽度的数值。
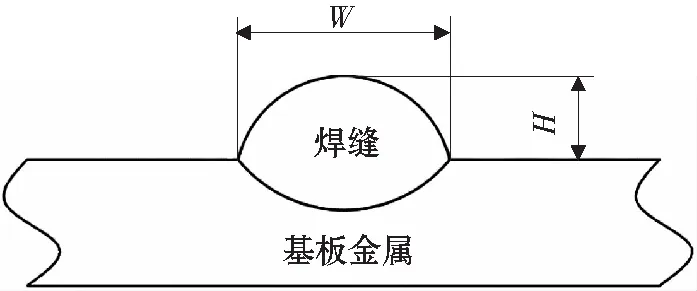
图2 焊道宽度和高度示意图
为减小测量误差以保证试验结果的可靠性和准确性,在焊道平整光滑处进行测量,每组数据均测量3次并取平均值。试验结果见表2。

表2 正交试验方案及结果
2 焊道尺寸预测模型建立
2.1 焊道尺寸BP神经网络的构建
为提高焊道尺寸预测精度,文中引入3层结构的神经元网络模型,神经网络模型输入层3个节点分别为电弧电压、焊接速度、送丝速度,输入层神经元个数为3;输出层节点为焊道熔宽和余高,输出层神经元个数为2;隐藏层神经元个数参考经验式(1)所示:
(1)
式中:S为隐藏层神经元个数;m为输入层神经元个数;n为输出层神经元个数;a为1~10之间的常数。
通过多次试验,比较不同隐藏层节点时的MSE(均方偏差特性函数),最终确定隐藏层层数为10层。文中创建的 BP 神经网络模型结构是3-10-2型,所建立的神经网络结构图如图3所示。
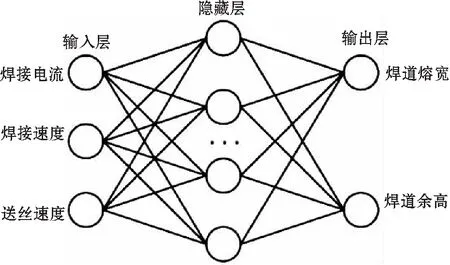
图3 神经网络结构图
神经网络每层之间存在连接权值,且各层均具有阈值和激活函数,利用激活函数正向传递输入值,求得输出值。BP神经网络最常用的激活函数有Sigmoid,Tanh和Relu,文中选择Sigmoid作为激活函数,如式(2)所示:
f(x)=(1+e-x)-1
(2)
使用Mapminmax函数完成数据的归一化处理,确保其不超过[-1,1]的取值范围,最后对网络输出的数据展开反归一化操作,从而获取真实的输出值。Mapminmax函数的具体公式如下:
(3)
式中:x为样本数据;xmin为样本数据中最小值;xmax样本数据中最大值;y为对x进行归一化后得到的数据;ymin和ymax为归化参数,默认值为-1和1。
根据网络调参经验确定网络训练函数为Levenberg-Marquardt算法,训练函数为trainlm,网络学习速率取0.01,最大训练次数为1 000次。
2.2 基于遗传算法的神经网络模型
BP神经网络的初始权值和阈值具有随机性,因此容易得到局部最优解而非全局最优解。文中采用遗传算法(Genetic algorithm,GA)来优化训练BP神经网络的连接权值和阈值,利用遗传算法全局搜索的特性,提高神经网络的泛化性能,优化BP神经网络权值初始化的随机性,提高模型预测的精度[10-11]。遗传算法优化神经网络模型具体包括种群初始化、选择适应度函数、选择算子、交叉算子和变异算子,具体结构示意如图4所示。

图4 遗传算法优化神经网络流程图
2.2.1初始化种群
初始化种群主要包括确定编码方式、种群规模及最大迭代次数。文中的个体编码采用二进制编码,每个个体均为一个二进制串,染色体的长度为:
L=S1×S2+S2+S2×S3+S3
(4)
式中:S1为输入层节点数;S2为隐含层节点数;S3为输出层节点数。文中创建的 BP 神经网络模型结构是3-10-2型,计算得到染色体长度为62。设定初始种群规模M=60,最大迭代次数G=200。
2.2.2适应度函数
为使BP神经网络在预测时,预测值与期望值的残差尽可能小,选择预测样本与期望值的误差矩阵的二范数作为目标函数的输出。
2.2.3遗传算子
选择算子是从父代群体中选择个体遗传到下一代群体中的方法,文中采用轮盘赌法选择算子,设定代沟值GGAP=0.95;交叉算子操作是指将2个不同个体按照某种方式相互交换而形成新个体的方法,文中选用单点交叉算子,设定交叉概率值Px=0.7;变异算子操作是以一定概率产生变异基因数,用随机方法选出发生变异的基因的方法,文中选取是基本位变异方式,设定变异概率值Pm=0.01。
遗传算法的优化过程是首先对初始化种群,选择部分优秀个体进入下一代种群,然后重复交叉操作和变异操作以产生新个体,如此循环即可保证神经网络得到最优解或达到设定的最大迭代次数。
2.3 遗传算法优化神经网络模型预测结果
为验证所提出的遗传算法优化神经网络焊道尺寸预测模型的性能,在迭代过程中跟踪误差值,如图5所示。误差值在迭代过程中随迭代次数递增而不断减小,这表明个体适应度在选择、交叉和变异过程中不断提高,最终个体逐渐接近目标值,遗传算法优化神经网络模型相比于神经网络模型具有更高的预测精度。
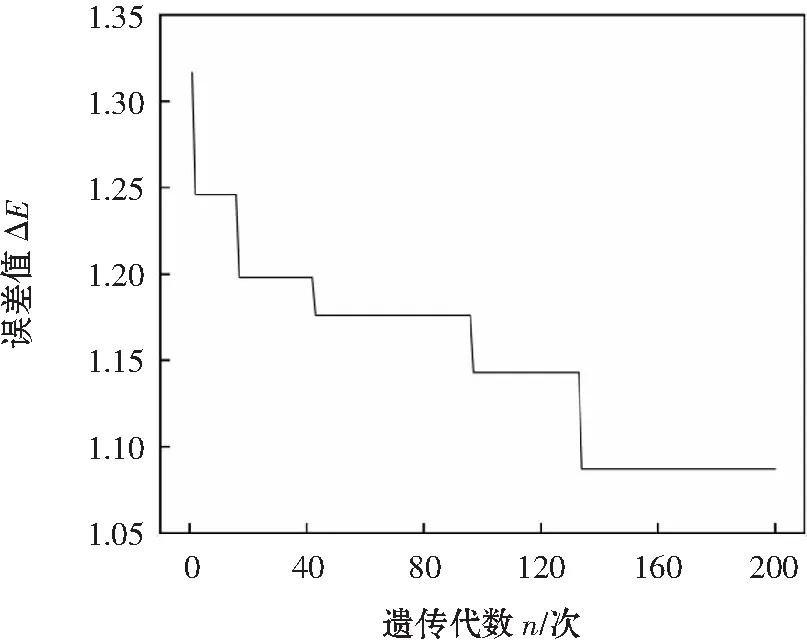
图5 迭代过程中误差变化
通过建立的遗传算法优化神经网络模型进行预测,并将预测结果与试验结果进行比较,从而得到预测样本输出误差值如图6~图7所示,焊道熔宽和余高的预测值与实际值相差较小。其中,如图8所示,预测熔宽和实际熔宽的误差平均值为2.05%;如图9所示,预测余高和实际余高的误差平均值为5.09%。表明采用该模型进行焊道尺寸模型预测具有较高的精度和可靠性。
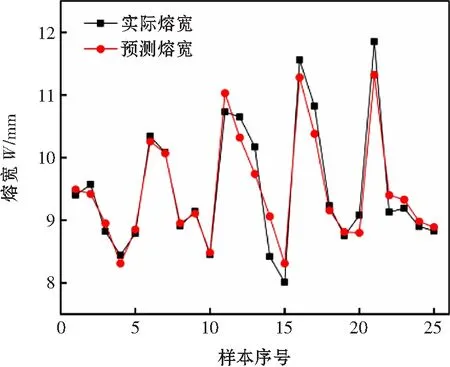
图6 熔宽预测值与实际值误差对比图
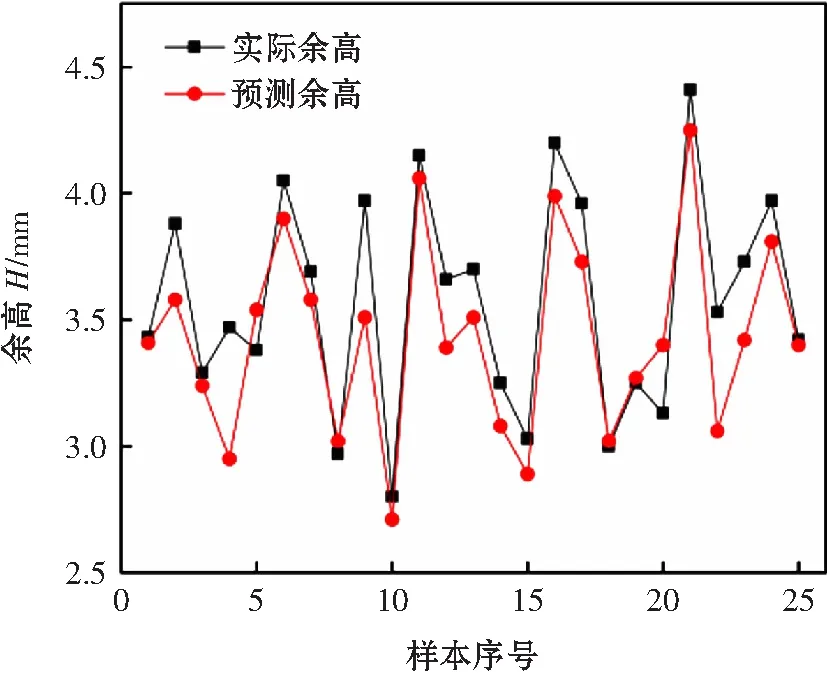
图7 余高预测值与实际值误差对比图
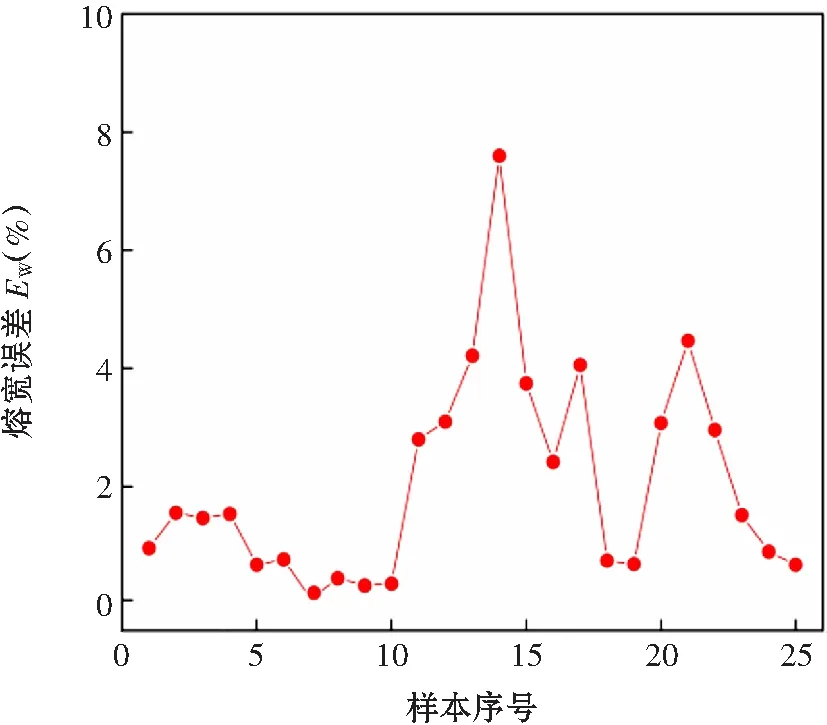
图8 熔宽预测值与实际值误差百分比图
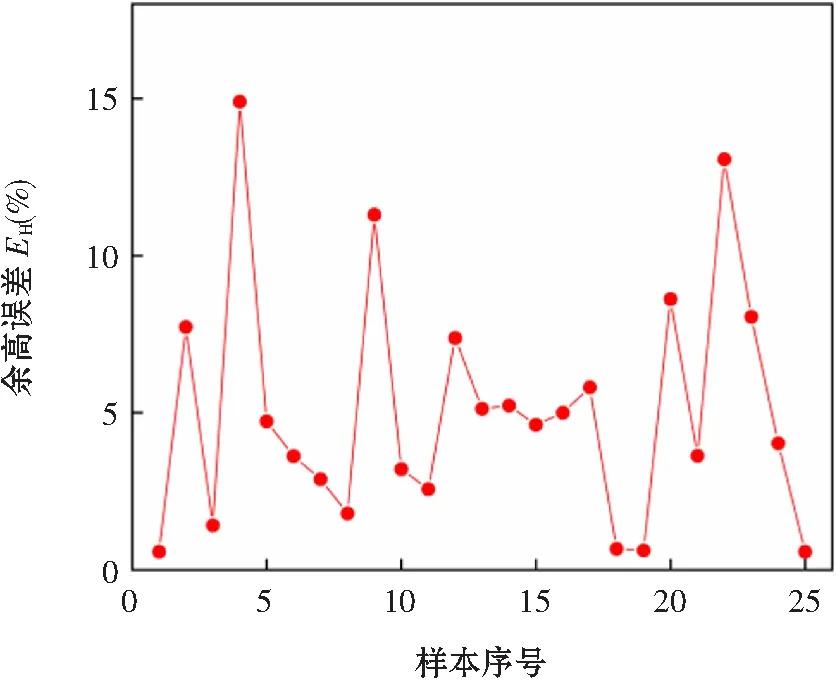
图9 余高预测值与实际值误差对比图
3 多层多道焊验证试验
3.1 试验流程
为验证遗传算法优化神经网络模型的精度,采取多道多层试验的方式进行验证。首先通过三维建模软件绘制3D模型,对模型进行等厚切片处理,然后依据3D模型尺寸并结合神经网络模型预测出焊道成形尺寸,进行层内及层间轨迹规划,最后设定机器人焊接工艺参数制造成形件。
3.2 多层多道成形试验
长方体预制件模型宽度为100 mm、长度为200 mm,高度为30 mm。根据所建立的GA-BP神经网络模型选取合适的焊接工艺参数,最终确定电弧电压为30.5 V、焊接速度8 mm/s,送丝速度为6.5 m/min。为改善焊缝侧表面的塌陷现象,层内路径采用轮廓偏置结合Zigzag的路径规划方式,即先焊外轮廓包络圈,再以Ziagzag的方式填充内部区域;为提高成形件尺寸精度,层间路径采用垂直交错堆积的方式,共堆积8层,层间冷却时间5 min。图10为多层多道试验实物图。成形件平均尺寸为宽度100.74 mm、长度201.32 mm、高度29.52 mm。成形件表面成形质量总体良好,表面层中间区域最高高度为29.87 mm,最低高度为29.35 mm,误差小于1 mm。但因为热积累和加工误差仍导致成形件出现侧面塌陷的现象,降低了成形件尺寸精度。

图10 多层多道成形图
4 结论
(1)文中结合正交试验电弧增材制造试验数据,选取电弧增材再制造影响焊缝尺寸的焊接工艺参数,建立以电弧电压、焊接电流、送丝速度为输入量,以焊缝的熔宽和余高为输出量的BP神经网络焊缝尺寸预测模型。
(2)采用遗传算法对BP神经网络的初始权值和阈值进行优化,寻求全局最优解。结果表明,经遗传算法优化的BP神经网络模型的预测误差较小,网络稳定性能较好,提高了模型的泛化能力和预测精度。建立预测模型可以在电弧增材再制造一定的焊接工艺参数范围内的实现焊缝尺寸的较精准预测。
(3)结合多层多道试验对模型进行验证,结果显示成形件成形良好,成形精度较高。文中建立的遗传算法优化神经网络模型在实际生产过程中对于选取合适的焊接工艺参数具有借鉴意义。

