压力容器内部缺陷有限元分析

金 良，冯 秀

（1.南京科技职业学院，江苏南京 210048；2.江苏省流体密封与测控工程技术研究开发中心，江苏南京 210048）

0 引言

力容器在长期处于承受高压状态下，其内部极易产生韧性破裂、疲劳、腐蚀、蠕变等内部缺陷[1-3]。当内部缺陷产生且无法从外观直接观察发现，在不及时进行定期检测的情况下甚至会产生爆炸危险，尤其使用在化工装置中的压力容器。迄今为止，对压力容器在线检测研究主要集中在超声波检测[4-5]和声发射检测[6-7]方面，但关于压力容器缺陷的有限元分析研究还比较鲜见。

为了能够对压力容器内部缺陷进行精准定位、精确测量以及精细分析高压载荷产生的影响，本文采用有限元方法对压力容器内部缺陷的离面位移和离面位移导数径向分布及缺陷尺寸、压力载荷对缺陷处离面位移一阶导数最大值影响进行分析。

1 有限元分析

1.1 力学模型

研究对象是内部带圆孔缺陷的平板封头，其半径r1=110 mm，厚度t1=18 mm，材料为45 号钢，弹性模量E=206 GPa，泊松比μ=0.3，其计算力学模型和具体结构尺寸如图1、表1 所示。

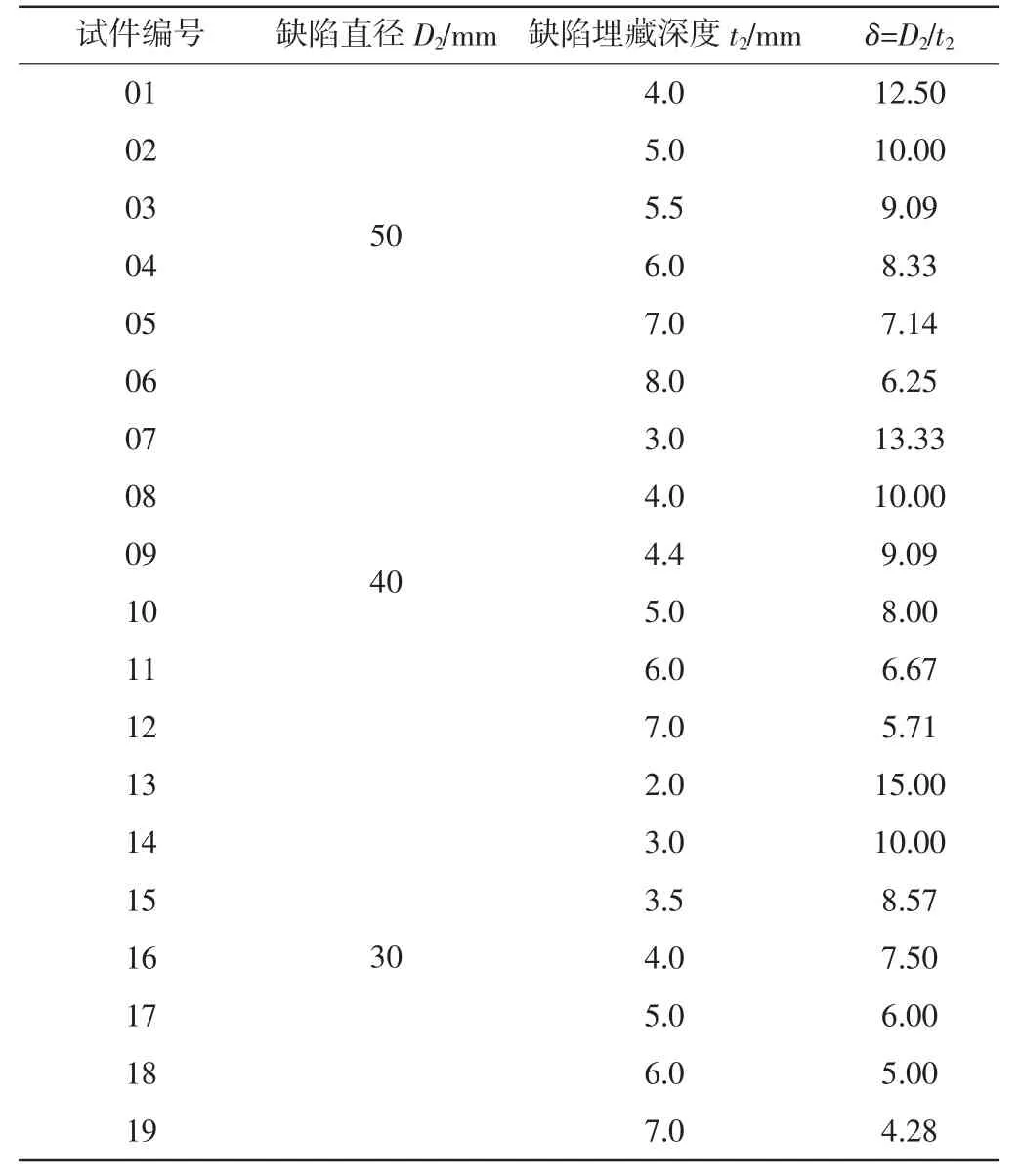
表1 缺陷尺寸

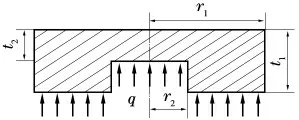
图1 力学模型

1.2 有限元模型

考虑到力学模型的对称性，建立四分之一的三维轴对称模型，以缺陷圆点为坐标轴原点，轴向为z 轴，径向为x 和y 轴（图2）。在对称边界上添加对称边界条件，在缺陷所在表面施加均布压力载荷q=0.1 MPa，采用六面体减缩二次单元C3D20R 进行结构化网格划分。

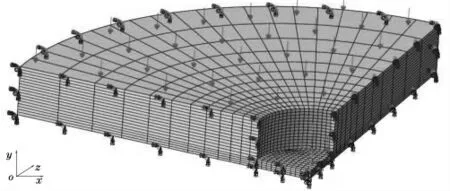
图2 FEA 分析模型

2 计算结果与分析

2.1 离面位移和离面位移导数径向分布

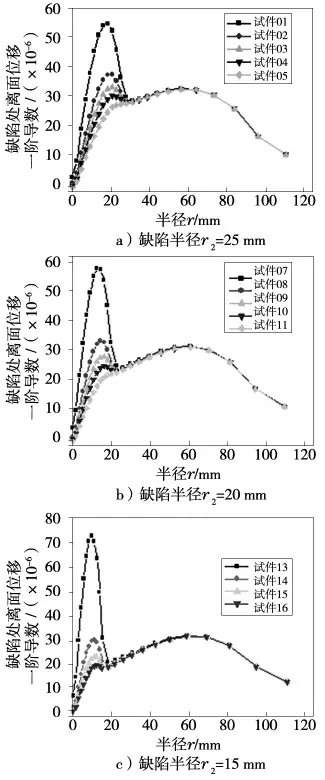
不同试件的离面位移云图和离面位移导数径向分布见图3和图4。

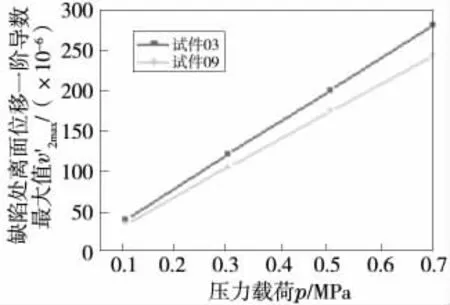
图3 表明，离面位移最大值在圆心处，且随半径增大逐渐减小。由图4 可知，当缺陷直径D2与缺陷埋藏深度t1之比δ≥9时，缺陷处离面位移一阶导数最大值w′2max大于封头非缺陷处离面位移一阶导数最大值w′1max，这时可以依据测量的离面位移一阶导数最大值来判断是否有缺陷；当δ<9时，w′2max

图3 离面位移云图（试件02，放大倍数200，红色位移最小，蓝色位移最大）

图4 离面位移一阶导数沿半径分布图

2.2 缺陷尺寸对缺陷处离面位移一阶导数最大值影响

图5 为缺陷尺寸对缺陷处离面位移一阶导数最大值影响。从此图可知，缺陷处离面位移一阶导数最大值w′2max随着缺陷埋藏深度t2增加在不断减小，且在δ≥9 时，w′2max随着t2增加在快速减小；7<δ<9 时，w′2max随着t2增加在缓慢减小；当δ<7 时，w′2max几乎不随着t2增加而改变。在同样深度t2下，缺陷直径D2越大，w′2max也越大。

图5 缺陷尺寸对缺陷处离面位移一阶导数最大值影响

2.3 压力载荷对缺陷处离面位移一阶导数最大值影响

图6 为试件03 和09 在压力载荷q 分别为0.1 MPa、0.3 MPa、0.5 MPa 和0.7 MPa 下，离面位移一阶导数沿半径分布。压力载荷对缺陷处离面位移一阶导数最大值影响如图7 所示。

由图6 和图7可知，离面位移一阶导数最大值随着压力增加呈线性增大。也就是说，在压力较小时，若缺陷处的w′2max＞w′1max或w′2max

图6 试件03 和09 在不同压力载荷下离面位移一阶导数沿半径分布图

图7 压力载荷对缺陷处离面位移一阶导数最大值影响

3 结论

（1）采用有限元方法对压力容器内部缺陷进行了数值模拟，得到了离面位移和离面位移导数径向分布，并分别研究了缺陷尺寸、压力载荷对缺陷处离面位移一阶导数最大值影响。

（2）离面位移最大值在圆心处，且随半径增大逐渐减小。只有当缺陷处离面位移一阶导数最大值大于封头非缺陷处离面位移一阶导数最大值时，才可以依据测量的离面位移一阶导数最大值来判断缺陷有无。

（3）缺陷处离面位移一阶导数最大值随着缺陷埋藏深度增加在不断减小，且当缺陷埋藏深度较小时，减小速率较大；当缺陷埋藏深度较大时，减小速率几乎为零。在同样深度下，缺陷直径越大缺陷处离面位移一阶导数最大值也越大。当缺陷直径与缺陷埋藏深度之比大于9 时，缺陷处离面位移一阶导数最大值大于封头非缺陷处离面位移一阶导数最大值。

（4）离面位移一阶导数最大值随着压力增加呈线性增大，且缺陷处离面位移一阶导数最大值大于封头非缺陷处离面位移一阶导数最大值或缺陷处离面位移一阶导数最大值小于封头非缺陷处离面位移一阶导数最大值。也就是说，在压力较小时，若缺陷处的w′2max＞w′1max或w′2max

以上研究结果为基于数字散斑剪切干涉法的压力容器内部缺陷检测的试验顺利进行奠定了基础。