例谈改造教材中的问题及建议
文∣刘兆伟
随着课改的不断推进,一线教师的教育教学理念也在不断改进中。在教学实践中,教师设计教学时不再拘泥于教教材,而是创造性地使用教材,甚至是自主改造教材。但教师在改造教材时,是否对教材进行了深入的解读,是否遵循了知识发展及学生认知发展的规律,改造后的教学设计能否实现对原有教材的超越是值得我们探讨的。现以苏教版小学《数学》的三节课为例,探讨在教材改造中存在的问题及改造教材的建议。
一、改造教材中存在的问题
(一)目标定位不当
【案例1】小数的性质
教师在教学教材中图1、图2、图3内容时,通过在整数末尾添0(或去掉0)引起整数大小变化,引导学生猜想:小数的末尾添上0(或去掉0)大小是否有变化?有的学生猜测会变,有的学生猜测不变。然后教师带领学生验证哪种猜想正确。验证共分四次:前两次验证与教材中的例4、例5相似;第三次
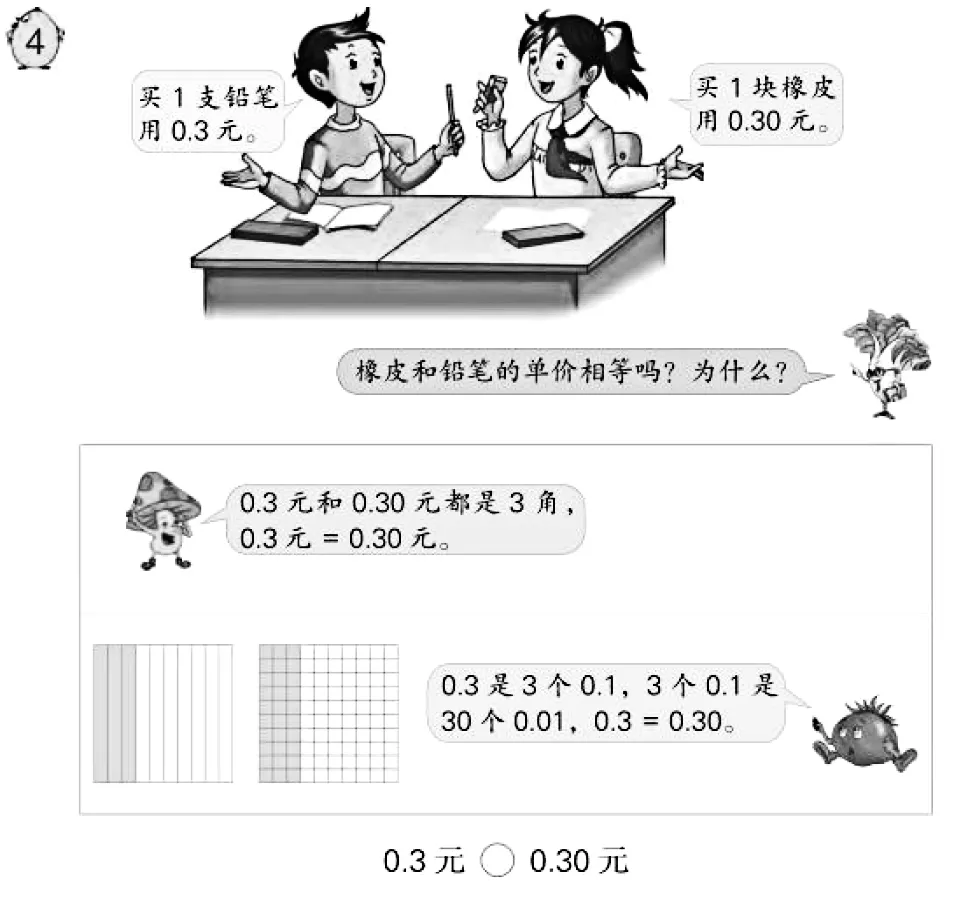
图1

图2

图3
让学生在等分成10份的相同长度的线段及等分成100份的相同大小的正方形上自己探究;第四次把探究的范围拓展到小数,验证1.4=1.40。教师引导学生通过四次举例验证,最终得出小数的性质。
教材中通过对两个具体例题的研究,让学生发现并归纳出小数的性质,从而培养学生的归纳、总结能力,这样的学习方式对于小学生而言是非常恰当的。但教学中,教师不满足于通过归纳得出结论的方式,他希望学生在获得活动经验的同时,验证意识也得到培养,所以改用提出猜想、验证猜想的方式进行教学。教师采用的验证方式是4次举例。实际上,对于有无数个研究对象的命题,无论举多少例子,都不能说明结论一定正确。通过这样的验证方式并不能得到确定的结论。验证意识的培养固然重要,但正确的验证方法同样重要,所以在上述案例1中,教师的教学目标定位是不恰当的。
(二)逻辑顺序混乱
【案例2】梯形的面积
图4中的例题,教师是按照教材的设计实施教学,图5中的例题教师做了改造,如图6所示。改动的地方有两点:一是操作的材料,教材中提供的是三组两个完全一样的梯形,而教师给学生提供的材料中有1个单独的梯形,还有2个完全一样的梯形;二是操作的目的,教材明确让学生拼成平行四边形,而教师则是让学生转化成学过的图形。不一样的操作带来了不同的结果,然后教师针对同一个梯形呈现了三种不同的转化方式,如图7所示。每一种方式都能得出梯形的面积,教师借此归纳出了梯形面积的计算公式。
教材的设计思路是通过图4中例题的教学让学生调用已有经验得出多种转化方法,并在比较中发现“倍拼法”在计算梯形面积时的方便与简洁。而图5中例题则是让学生将“倍拼法”由具体推广到一般,从而发现这种方法可以适用于所有的梯形面积的计算,学生在此过程中掌握从特殊到一般的归纳推理的方法。教材的设计意图十分清晰,教师在教学时保留了图4中例题,改造了图5中例题,但选择用1个梯形转化成其他图形的方法在图4中例题的教学中就会出现,改造后的图6中例题与原来的计算方法存在重复设计之嫌,并且仅根据一个梯形的不同转化方法就归纳得出梯形的面积计算公式,图4中例题相比不具有一般性。所以,在上述案例2教学中,教师的设计在逻辑上是混乱的。

图4

图5

图6

图7
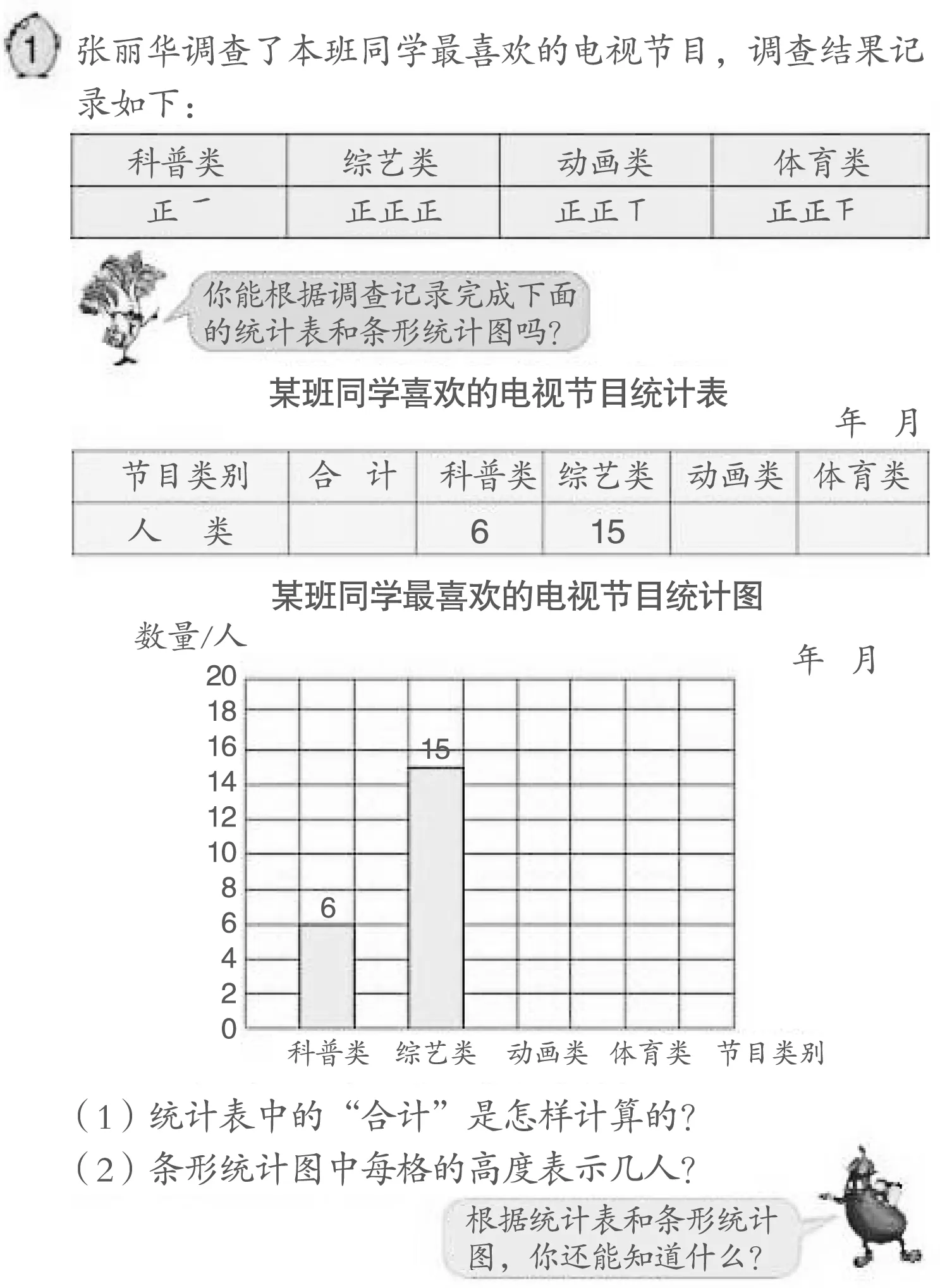
图8

图9
(三)价值认识偏差
【案例3】统计表与条形统计图
教师在教学图8中例题后,并没有进行“练一练”的教学,而是围绕条形统计图的认识开展了不同形式的设计。先将统计的范围由班级扩大到年级,再扩大到全校,引导学生认识“随着统计数据的不断增大,条形统计图中表示数量的纵轴一格所代表的数也需要不断增大”,最后教师展示多种生活中出现的条形统计图,让学生理解每一种条形统计图所表达的意思,感受条形统计图的价值。
图8中的例题设计意图是让学生掌握将收集的原始数据整理成统计表,再根据统计表绘制成统计图,最后对统计图进行简单数据分析。而“练一练”的目的则是让学生根据图8中例题的程序真实地经历收集数据、整理数据、描述数据、简单分析数据的完整统计过程。这里的“练一练”是十分重要的,而教师将教学设计重点放在了条形统计图的绘制及分析上,忽视了让学生经历完整的统计过程,轻视了从原始数据到整理成统计表这一环节,其对“练一练”价值的认识存在偏差。
通过以上分析,我们可以发现,这三个案例中,教材的设计思路是符合学生认知发展规律和知识教学顺序的。教师在教学这些内容时,如果能深入分析教材,理解教材中每一个环节的设计意图,并按照教材的设计意图实施教学,是能够让学生在原有的基础上得到较好的发展的。教师如果没有更好的方案,就应尊重教材的设计思路,将静态的教材动态化呈现,丰富学生的学习过程。
二、改造教材的教学建议
不是所有的教学内容都需要严格地遵循教材的设计思路来实施教学。教材本身处于不断的变动、完善中,其变动依据除了数学知识的本质与学生认知发展的规律及学生的年龄特点外,还有部分来自一线教师的教学实践。
(一)发展理性思维,凸显学科本质
理性思维具有明确的思维方向和充分的思维依据,是一种建立在逻辑推理基础上的思维方式。数学在形成人的理性思维的过程中发挥着不可替代的作用。小学数学学习是学生理性思维发展的基础阶段,教材的知识编排受小学生的思维能力及年龄特点约束,对学生理性思维的要求较低,但有时不利于学生理性思维的培养。在教学中,教师要有意识地对学生进行理性思维的渗透,培养学生良好的思维习惯。
在案例1中,教材是通过对实际生活中两个例子的研究,由“量的相等”归纳出小数的性质,这样得到的结论是基于生活经验。教师想要理性地解释小数的性质,需要借助于分数的基本性质,但因为教材将分数的基本性质安排在小数的性质之后学习,这就导致教师暂时无法从逻辑上解释小数的性质。但学生在学习小数的性质之前,已经学过小数的意义及其组成,这些知识可以成为学生理解小数的性质的基础。笔者建议,在归纳出小数的性质后,教师可以让学生结合具体的例子,从小数的意义及组成的角度来初步理性地解释小数的性质,如0.3中的3表示3个0.1,无论在它的末尾添几个0,其中的3仍然表示3个0.1,所以其大小不变。让学生多一点理性思考,至于逻辑形式的证明,则可以在学生学完分数的基本性质后再来弥补。
(二)提供学习空间,改善学习方式
学生是学习的主体,课堂教学是否有效,取决于学生的学习活动是否有效,而学生的学习活动是否有效取决于教师能否在课堂上给学生的思考留出足够的时间与空间。只有提供足够的学习空间,学生才能获得生动、活泼、全面的个性发展。教材一般会循序渐进、程序清晰地设计学习路径。清晰的知识编排顺序不仅有利于教师的教,而且有助于学生的学。但顺序的过于精细化可能会导致留给学生的学习空间不足,所以在教学中,教师要合理地为学生提供足够大的学习空间,充分调动学生学习的积极性。
在案例2中,学习梯形面积之前,学生已经在探索长方形、正方形、平行四边形及三角形的面积计算公式的过程中积累了大量的活动经验,根据这些经验,学生完全能够独立地探索出梯形的面积计算公式。教材安排的两个例题虽然结构严谨,但留给学生的学习空间是非常狭窄的。笔者建议将本课中的两个例题合二为一,直接提出大问题“梯形的面积可以怎么计算”,给学生提供多个梯形纸片,其中有两个是完全一样的;也有上底、下底、高都一样,但形状不一样的;也有单独一个的。让学生先自主选择所需材料,独立探索梯形的面积计算公式,再相互交流,逐步归纳出梯形的面积计算公式。这样的学习任务能给学生提供更大的学习空间,并具有适当的挑战性,学生能够获得更大的发展。
(三)引发学习需要,培养学习情感
学习需要是学习行为的内驱力,当学生的学习需要被充分激发时,学生才能积极、主动地投入学习活动中。教材编排主要考虑的是数学知识的逻辑体系及学生的认知规律,在有些学习内容的安排中会忽视学生的学习需要。对于这样的学习内容,如果按照教材安排的程序教学,学生会缺乏学习兴趣,他们的学习行为将是被动、机械的。因此,教师要想方设法地利用各种方式来激发学生的学习兴趣,从而使学生积极地、主动地参与探索新知的学习活动。
在案例3中,教材中的例题让学生将已经收集好的数据整理成统计表并绘制成统计图,这样的学习任务,难以引起学生学习的兴趣,无法产生学习的需要。而“练一练”中的活动需要每一个学生参与其中,所收集到的数据也是真实的,无论在形式上还是内涵上都能引发学生的学习兴趣,学生更乐于参与这样的学习活动。所以,笔者建议将“练一练”中的习题改为例题来教学,让学生经历完整的统计过程,在此过程中掌握将原始数据整理成统计表且依据统计表绘制成统计图的方法,真切地感受统计的价值。
在教学设计前,我们要全面、深入地分析和解读教材,对于教材中合理的设计,我们可以遵循教材的设计思路,将静态的教材动态化,丰富学生的学习过程,增强学生的学习体验。对于教材中不合理的地方,要结合理论与实际,深入思考并探寻更为合理的学习路径,并在实践中加以检验与调整,以促使学生获得更好的发展。

