一类具有时滞和尺度结构的捕食种群系统的最优收获
毛瑾晖
(兰州交通大学 数理学院,甘肃 兰州 730070)
生态学是与人类生活密切相关的科学,人类现阶段面临的环境、资源及人口问题都是其所研究的内容,对生物种群模型进行研究可更好地推动生态学的发展。众多学者在种群模型上颇有建树[1-3],他们使用精炼的数学语言来表达生物现象,建立对应的数学模型,解决生态学中的问题。文献[4]研究基于尺度结构的捕食-被捕食模型,分析模型解的特点;文献[5]研究了具有尺度结构的种群模型,更为细致地分雌、雄个体对最优不育问题进行分析,但仅考虑了单种群问题。在生物数学最优控制方面,文献[6]利用切锥、法锥及Ekeland变分原理等理论对较一般的种群进行研究。雒志学等[7]更为深入地分析了在周期环境下具有年龄结构的种群最优控制问题。文献[8]对捕食-食饵种群的最优控制对进行讨论,将单种群推广为两种群,使模型更具有应用性。文献[9]也对捕食种群动力系统进行了进一步分析,但未考虑时间滞后这一因素。在建立模型时,时滞[10-11]也是重要的影响因素,杜明银[12]、戴勇[13]在具有年龄结构的种群模型的基础上考虑时滞因素,但他们研究的为周期解问题,并未分析最优收获问题。当前,生物种群模型中考虑时滞因素的较少,本文在文献[8]的研究基础上,同时考虑时滞和尺度结构,建立了基于时滞和尺度结构的捕食-被捕食模型,分析了状态系统解的存在唯一性,并讨论最优收获问题。
1 模型的建立
本文建立基于时滞和尺度结构的捕食种群系统
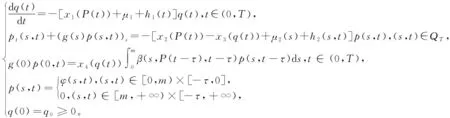
(1)
其中


U={(h1,h2)∈L∞(0,T)×L∞(QT)|0≤h1(t)≤N1,a.e.t∈(0,T),
0≤h2(s,t)≤N2,a.e.(s,t)∈QT},
N1,N2都是大于零的常数。
考虑控制问题:
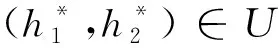
做以下假设:
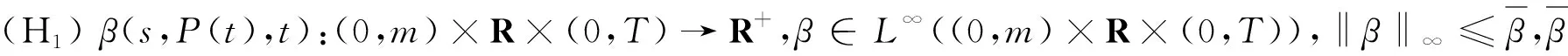
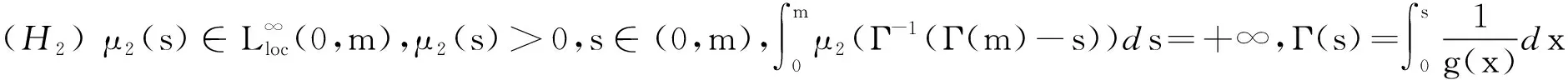
(H3)g(s)∈C1[0,m],0 (H4)y2(s)∈L∞(0,m),y1和μ1为正常数; (H8)xi关于其变量及一阶导数均满足Lipschitz条件,i=1,2,3,4; (H9) 所有参数和变量在其定义域外均为零。 首先选择M,满足 定义解空间 其次定义映射L:X→X使得L(q,p)=(L1(q,p),L2(q,p))。 设在t0时刻捕食种群个体的尺度为s0,经过一段时间θ=t-t0后,尺度变为s,则必有s=Γ-1(Γ(s0)+θ)。应用特征线法,得 由(1)中的第二式,可得 因此,得 故此得下述解 (2) 当0 (3) 取s0=Γ-1(Γ(s)-t),t0=-τ,有 (4) 当t>Γ(s)时,取s0=0,t0=t-Γ(s),定义B(t)=g(0)p(0,t),得 (5) 当t-τ≤Γ(s)且t>Γ(s)时,取s0=0,t0=t-τ-Γ(s),得 (6) 当t-τ>Γ(s)时,取s0=0,t0=t-τ-Γ(s),得 (7) 将(3)~(7)代入(1)式得 其中θ1,θ2,θ3,θ4定义如下: 利用特征线法得到上述解,因此式(3)和式(5)联合得出式(2)第二式的表达式。若(q(t),p(s,t))是映射L的不动点,且满足q(t)≥0,p(s,t)≥0,则该点为状态系统(1)的解。 定理1 设(H1)~(H9)成立,(h1,h2)∈U,若T足够小,则状态系统(1)存在唯一的解(q,p)。 证明由特征线法得映射L的不动点是状态系统(1)的解,即只要证明映射L有唯一的不动点,故证映射L是压缩映射。 第1步 证明L映射到自身。 其中,C1是一个与参数h1与x1有关的常数。 x3(q(t+r-Γ(s)))]p(Γ-1(r),t+r-Γ(s))dr|ds≤ 其中,C2是一个与参数h2,xi,i=2,3,4,β和g的界限及常数因子有关的常数。因此当T足够小时,L映射到自身。 第2步 讨论映射L的压缩性。 ‖L(q1,p1)-L(q2,p2)‖L∞(0,T)×L∞(0,T;L1(0,m))= ‖L1(q1,p1)-L1(q2,p2)‖L∞(0,T)+‖L2(q1,p1)-L2(q2,p2)‖L∞(0,T;L1(0,m))= 接下来考虑 其中,Ci(i=3,…,9)都是仅与参数h1,h2,xi(i=1,…,4),β和g的界限及常数因子有关的常数。因此选择足够小的T,可得映射L是空间X上的一个压缩映射,故T存在唯一的不动点,即状态系统(1)存在唯一解。 本节将导出最优收获问题的最优性条件,下式为状态系统(1)的共轭系统 (8) 对任意函数α1∈L∞(0,T),α2∈L∞(QT)共轭系统的弱解满足 其中函数φ1和φ2满足 据定理1的证明方法可证得共轭系统解的存在性。记(qh1,ph2)和(ηh1,ζh2)分别是共轭系统和状态系统对应于给定的(h1,h2)∈U的解。定义映射Fi:L1(0,T)×L1(QT)→L∞(0,T)×L∞(QT)为 同时除以ε并令ε→0+,即 (9) (10) 通过计算可得(Iε(t),fε(s,t))满足方程 接下来,证明当ε→0+时,(Iε(t),fε(s,t))→(0,0)。 因为xi(0)=0(i=1,2,3),x4(0)=1得到下述关于(I(t),f(s,t))的极限系统 故该系统在(0,T)×QT上有唯一解(I(t),f(s,t))=(0,0)。 将共轭系统(8)前两式分别乘以ω(t)和z(s,t),且在(0,T)和QT上积分,通过化简及利用(8)式、(10)式可得 结合已知式子,故得 由法锥元素的结构可得(8)式。 本文建立了一类具有时滞和尺度结构的捕食-被捕食种群模型。将单种群模型推广至两种群模型,并考虑时滞因素,分析了捕食种群具有尺度结构的情况,使种群模型与现实更加结合。利用不动点定理证明了该系统解的存在唯一性,由切锥法锥概念推导出最优收获的必要条件。但生物种群受各方面影响,如空间、温度、气候等,应建立多维度影响因素的模型,以更好地描述贴合实际。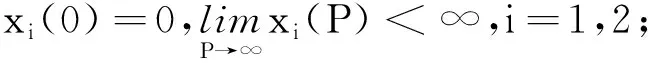
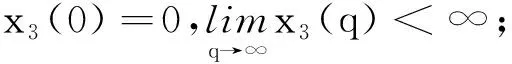
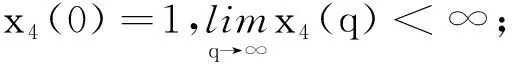
2 解的存在唯一性

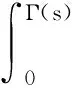
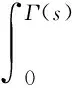


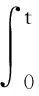

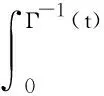


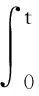

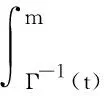
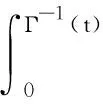
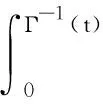
3 最优控制的必要条件
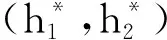
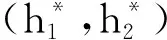
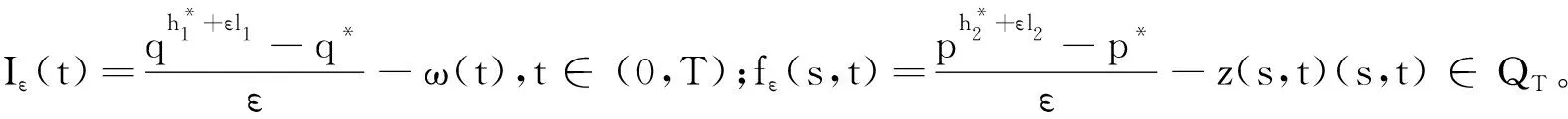

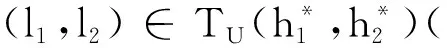
4 结论

