基于逐次最邻近插值的动力电池电压模拟方法

张晋 易吉良 陈松伯 李中启

摘 要：动力电池模拟系统是新能源汽车测试平台等工业领域的重要装备，而电池模型是该系统能否精确模拟电池特性的关键环节。为兼顾数据容量和给定电压的精确性，提出逐次最邻近插值算法应用于电池模型数据查表，该方法根据动力电池在电池电荷状态（State of Charge，SOC）初始段、平稳段和末尾段的输出特性，建立了三个不同分辨率的模型子表，并借鑒最邻近插值算法的计算量小和容易实现的优点，采用对模型表逐次迭代分区，进而逼近实际SOC和采样电流对应的电池模型给定电压值，达到细化电池模型表分辨率效果。讨论了迭代次数选择对算法精度的影响，并采用不同抽样比例降低模型数据容量，对不同容量数据表做了大量实验，实验结果表明，本文方法在低分辨率数据样本条件下仍能保持高精度。

关键词：查表；最邻近插值算法；动力电池；SOC；给定电压

*基金项目：湖南省自然科学省市联合基金资助项目（资助号2019JJ60055）湖南省教育厅重点科研项目（资助号18A272）

0 引言

随着能源危机与环境污染压力的加大，新能源汽车特别是纯电动汽车成为各国政府政策支持和各汽车厂商大力发展的解决方案[1]。英、德等国政府宣布将于2025—2040年内全面禁售传统燃油汽车，在2017年9月举行的中国汽车产业发展国际论坛上，工信部相关负责人表示，我国也已启动传统燃油车的退出计划。

测试平台采用动力电池模拟电源能够克服直接采用动力电池带来的成本高和不便利的缺点，并解决使用普通稳压电源不能模拟动力电池特性的问题，因此，动力电池模拟电源是电动汽车测试平台不可缺少的装备。电池模型是模拟电源实现高逼真度电池伏安特性的关键要素，直接影响电源模拟电池的效果。建立电池模型主要任务是根据电池的SOC和负载电流给出模拟电源输出端口的参考电压，现有的模拟电源电池模型建立方法主要有：①用已有标准电池模型获得电池特性参数；②采用分段拟合电池伏安特性曲线[4]；③查表法。其中方法①使用电池模型获得特性曲线的精度高，但模型中含有指数函数，在芯片中实现难度高，需要大量的计算且对芯片要求也较高，不适用于动态系统。方法②虽然减少了计算量，但是误差也显著增大，如果使用高阶方程可以提高精度，但是在工作电流大范围变化的工况下，则需要拟合多条曲线，运算量大且算法时间长，无法跟上系统的实时动态响应。方法③需要先得到V-I特性曲线，再通过曲线离散化获得需要的数据，计算量小[2]。

为获得足够的模拟精度，查表法往往需要采用大数据样本，但这会对系统容量提出很高的要求。为了减少数据容量查表法一般会使用插值算法，而传统方法如最邻近插值算法和双线性插值算法要么精确度不够，要么算法计算量大，系统实现成为难题。为了减少数据样本和运算量，同时满足输出精度要求，本文通过改进最邻近差值算法，提出了一种基于逐次最邻近差值算法的动力电池模拟系统的输出电压给定方法，并通过仿真实验证明了该方法的有效性。

1 背景知识

1.1 动力电池模拟系统

典型的动力电池模拟系统包括双向PWM整流器和双向DC/DC变换器[3]，如图1所示。

1.2 常用插值法

电池模型表类似于数字图像处理中的像素灰度表，因此电池模型查表可以借鉴图像处理中的插值算法，其中常用的插值算法包括最邻近插值算法和双线性插值算法。最近邻插值算法[4]是依据距离最短原则将实际坐标值映射到模型表中的坐标，并将模型表中该坐标的电压值作为电池输出的电压。如图2所示，U点为运行过程中获取的待求输出电压，U1（1）、U2（1）、U3（1）、U4（1）是模型表中邻近U点的4个坐标对应的电压值，因U1（1）的坐标位置与U点的距离最短，因此将U1（1）的值赋给U点作为模拟电池的输出电压值。

2 逐次最邻近插值算法

2.1 系统工作流程

图3为本文动力电池模拟系统电压给定方法的流程图，由图可见，系统包括SOC估算、动力电池模型表和插值算法3个部分，其中，SOC估算是根据初始值SOC*以及采集的负载电流i，采用安时法实现对动力电池的SOC值估算。

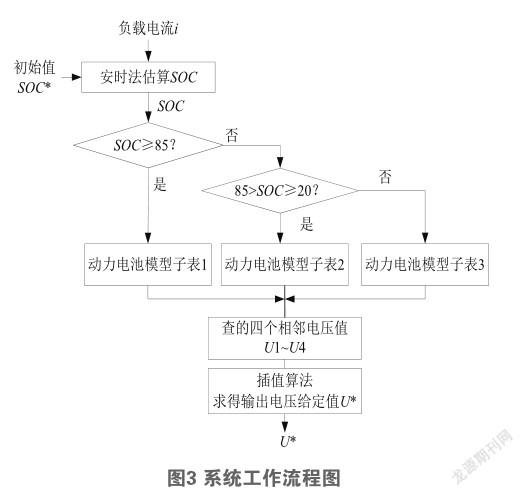
考虑动力电池在SOC较大和较小时，输出电压变化较快，因此将动力电池模型表分成3个子表，即：当SOC≥85%时，称为模型子表1；当85%>SOC≥20% 时，称为模型子表2；当SOC<20%时，称为模型子表3。因为动力电池V-I特性曲线在SOC值为5%～20%区间以及85%～100%区间起伏大，这使得离散后的两个相邻坐标之间的电压值相差大；而20%～85%区间V-I特性曲线变化不大。因此，子表1和子表3采用SOC分辨率dSOC较小的模型表，而子表2采用SOC分辨率dSOC较大的模型表，同时电流的变化对电压的影响不大，所以三个模型表负载电流i的分辨率di相同。

由图3可以看出，根据不同的SOC选用对应的动力电池模型子表后，利用估算的SOC和采集的电流i便可确定待求输出电压在模型子表中的4个相邻电压值，利用本文提出的逐次最邻近插值算法对这四个电压值进行迭代运算，不断更新坐标和对应电压值，最终输出给定电压值U*。

2.2 逐次最邻近插值算法原理

由上节可知，逐次最邻近插值算法根据估算的SOC和采样的负载电流i查找动力电池模型子表，进而得到四个邻近电压值U1～U4即点U1（1）、U2（1）、U3（1）、U4（1），将这四个点看成一个正方形，按照如下步骤实现逐次最邻近插值算法。

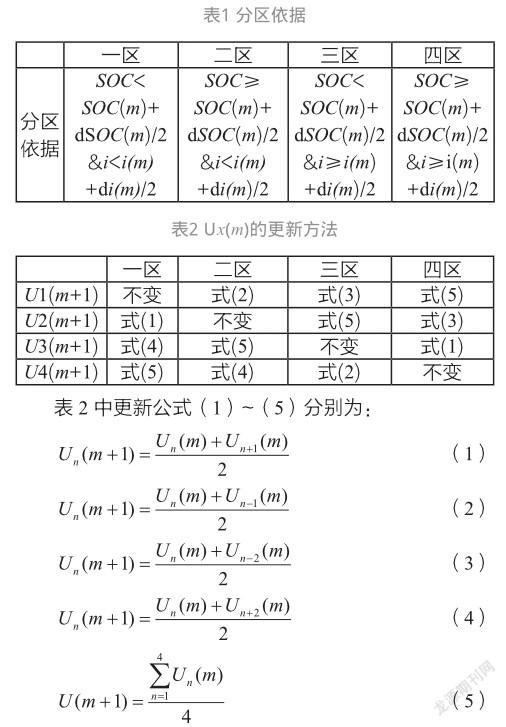
1）以表1的分区依据将正方形平均分成四个小正方形即四个区，设m=1。

2）将与待求点U位于同一个区的Ux（m）（x为1～4中之一）作为不变点。

3）用表2更新待求点U所在区的四个顶点U1（m+1）、 U2（m+1）、U3（m+1）、U4（m+1）。

4）用（6）～（10）式更新分区依据。

5）令m=m+1，若m

公式（1）～（5）分别描述了不变点左侧、右侧、上方、下方以及对角点的电压更新方法。

每次迭代后需要根据所在分区对坐标SOC和i进行更新，1～4区的更新公式分别为公式（6）～（9）。

当m=M时，用式（5）计算动力电池模拟系统的输出电压给定值U*，即Ux（m）的均值。

3 实验及分析

3.1 模型表容量的确定

查表法往往要采用大数据样本，但这会对系统容量提出很高的要求，在保证输出电压精度的情况下，尽量减少模型表的数据容量，可以减少查表时间和降低系统成本。

3.2 与最邻近插值法的对比

采用MATLAB&Simulink中的标准动力电池模型产生基准表数据，使用双线性插值算法查基准表获取基准值。以D2抽取表和基准表作为数据样本，采用最邻近差值算法和本文方法计算电池模拟系统的给定电压，分析两种方法得到的给定电压与基准值的绝对误差的绝对值。以固定SOC（5%≤SOC≤100%的随机值）和不同电流（-100 A≤i≤100 A随机产生的100个值）进行实验，两种方法查表得到的给定电压与基准值电压的绝对误差的绝对值，部分结果如图5所示。

由图5a可以看出，在SOC为13.7%的条件下，本文方法查基准表的绝对误差小于0.000 4，而相同条件下最邻近方法的绝对误差在1.2以内。对D2抽取表本文方法的查表绝对误差小于0.03，而最邻近方法的绝对误差在1.7以内。所以在相同的查表条件下本文方法具有更高的准确度。同时该结果表明，因为13.7%的SOC值处于动力电池特性曲线变化大的区间内，这使得离散抽取后的两个相邻坐标之间的电压值相差大，从而致使最邻近方法的查表误差变大。而本文方法通过逐次逼近修正了因数据表分辨率降低造成的误差。

由图5b可以看出，在SOC为39.5%的条件下，本文方法查基准表的绝对误差小于0.000 2，而最邻近方法的绝对误差在0.2以内；对D2抽取表本文方法的绝对误差小于0.02，而最邻近方法所得的绝对误差在0.6以内，所以在该查表条件下本文方法同样具有更高的准确度。因为SOC为39.5%时处于动力电池特性曲线平滑的区间内，这使得最邻近查表误差比SOC为13.7%时得到查表误差小。

本文还在SOC值为5%～100%的条件下进行了大量实验，结果表明本文方法查D2抽取表的绝对误差的绝对值均小于0.03，相较于最邻近方法，在给定电压准确性方面具有明显优势，限于篇幅不再给出图示。同时，相较于双线性算法，本文方法只需进行几次迭代加减计算，需要的时间短且实现容易。

4 结语

本文提出的基于逐次最邻近插值的动力电池模拟系统的输出电压给定方法，在模型表的数据容量缩减了98.4%的条件下，相比较采用最邻近插值算法的给定电压精度从个位提升至百分位，减少了查表时间和降低了系统成本。插值算法的迭代次数4～5次就可以满足电池模拟的要求，迭代的次数增加可以提高查表精度。本文方法在边界点的处理还不够完善，对边界点查表过程进行优化处理可以增强方法的稳定性，便于实际应用。

参考文献：

[1] GENIKOMSAKIS K N，GUTIERREZ I A，THOMAS D，et al. Simulation and design of fast charging infrastructure for a university-based e-car sharing system[J]. IEEE Transactions on Intelligent Transportation Systems，2017 （99）：1-10.

[2] 唐金成，林明耀，张蔚.光伏电池阵列模拟器的研究[J].江苏电器， 2007（06）：10-12+28.

[3] 张丙寅.动力电池模拟电源控制系统研究[D].哈尔滨：哈尔滨工业大学，2012.

[4] WANG Y， WAN W， WANG R， et al.An improved interpolation algorithm using nearest neighbor from VTK[C].Audio Language and Image Processing （ICALIP）， 2010 International Conference on，2010.

[5] 赵煌，彭勇.双线性插值算法的优化及其应用[J].电视技术，2012， 36（17）：30-32.

[6] 莫林利，赵秀绍，郑伟，等.二维表查找和双线性插值算法的设计与应用[J].华东交通大学学报，2015，32（05）：93-98.

[7] 何志超，杨耕，卢兰光，等.一种动力电池动态特性建模[J].电工技术学报，2016，31（11）：194-203.