基于机器学习算法的盾构掘进地表沉降预测方法

陈仁朋 戴田 张品 吴怀娜

摘要：针对有限元、地层损失率等方法难以考虑多参数耦合作用情况下的地表沉降预测的问題，基于BP神经网络（BPNN）和随机森林算法（RF）两种机器学习算法的多参数、非线性拟合能力，提出了预测盾构掘进过程中地表最大沉降以及纵向沉降曲线的预测方法.通过粒子群算法（PSO）确定机器学习算法的最优超参数，通过k折交叉验证方法提高预测方法的鲁棒性.结果表明BP神经网络的预测结果误差较大，难以预测到较大的地表沉降，随机森林算法能够准确预测地表最大沉降和纵向沉降曲线.

关键词：盾构隧道；地表沉降；机器学习；优化

中图分类号：U455.43；P642.26文献标志码：A

基金项目：国家自然科学基金重点项目（51938005），National Natural Science Foundation of China（51938005）；创新平台与人才计划-湖湘高层次人才聚集工程-创新团队（2019RS1030）

Prediction Method of Tunneling-induced Ground Settlement Using Machine Learning Algorithms

CHEN Renpeng1，2，3，DAI Tian1，2，3，ZHANG Pin4，WU Huaina1，2，3

（1. Key Laboratory of Building Safety and Energy Efficiency of Ministry of Education，Hunan University，Changsha 410082，China；2. National Center for International Research Collaboration in Building Safety and Environment，Hunan University，Changsha 410082，China；3. College of Civil Engineering，Hunan University，Changsha 410082，China；4. Department of Civil and Environmental Engineering，Hong Kong Polytechnic University，Kowloon，Hong Kong，China）

Abstract：It is difficult to consider the prediction of ground settlement under the coupling effect of multiple fac-tors for the finite element method and formation loss rate. Based on the multi-factor and nonlinear fitting ability of back-propagation neural network（BPNN）and random forest（RF），these two machine learning algorithms are adopted to predict the tunneling-induced ground settlement. The optimum hyper-parameters of the two machine learning al-gorithms are determined by particle swarm optimization（PSO），and k-fold cross validation method is used to improve the robustness of the prediction method. The prediction results indicate that the prediction error of BP neural network is larger and it’s hard for BP neural network to predict the large settlement. The random forest algorithm can accu-rately predict the maximum settlement and longitudinal ground settlement curve.

Key words：shield tunnel；ground settlement；machine learning；optimization

土压平衡盾构由于适应地层广，对地面交通影响较小，是城市地铁隧道建设主要工法.盾构掘进过程中扰动地层，改变地层应力场，使地面产生沉降，威胁周边建筑物和构筑物的安全.准确预测地层沉降能够降低盾构掘进过程中引发的安全风险[1-2].现有的地表沉降预测方法可以分为：1）经验和半经验公式[3-4]；2）解析法[5]；3）数值模拟[6-7]；4）模型试验[8]；5）机器学习算法预测[9-12].

经验和半经验公式法可以描绘地表沉降的一般形态[3-4]，但由于不同地层经验参数的取值差异性较大，因此预测的沉降分布在较大范围内，且预测结果的准确性不能保证.解析法的计算模型较为简单[5]，仅考虑地层参数和土体损失率，无法考虑盾构施工因素，不能真实准确地反映盾构掘进与地层之间的相互作用，且计算过程复杂，难以在工程实际中应用.数值模拟方法由于可以考虑到土体性质、盾构机与土体之间的相互作用、盾构掘进参数等因素，现阶段被广泛应用于研究盾构掘进过程中的地层响应以及对周围环境的影响[6-7]，该方法中本构模型参数确定困难，并且大尺度的模拟计算耗时较多.而模型试验广泛用于研究盾构掘进过程中沉降的演变机理[8]，但考虑的因素有限，且成本较高，无法用于地表沉降的实时预测.盾构掘进过程引起的地表沉降涉及到多参数的耦合，上述方法均难以实时准确预测.机器学习算法能利用计算机构建概率统计模型，从大量数据中学习规律和模式，并能考虑传统物理模型中难以考虑的因素，实现多参数跨单位和量纲的高维度拟合.且沉降预测模型训练完成后使用方便，符合实际工程及时准确获取地表沉降的要求.近年来开始应用于预测盾构掘进引起的地表沉降[9-12].

人工神经网络、支持向量机和随机森林算法是现阶段用于预测盾构掘进引起的地表沉降的主要机器学习算法. Shi等[13]首次使用人工神经网络的方法预测盾构掘进引起的地表最大沉降. Santos等[14]利用人工神经网络模型分析掘进参数与地表沉降间的关系，论证了该方法的可行性.为了提高人工神经网络的预测精度，Ahangari等[15]提出基于遗传算法优化的人工神经网络.支持向量机方法能基于少量数据做出准确预测，Wang等[16]采用小波函数与支持向量机结合的方法对地表监测点的沉降变形的过程进行预测.随机森林在盾构掘进引起的地表沉降的预测中性能表现较好[17].在预测沉降问题中，机器学习算法的超参数多通过手动调节，且缺乏算法的性能对比.使用优化算法对机器学习算法的超参数进行选取，能提高机器学习算法的预测性能.

本文提出了基于粒子群算法（Particle Swarm Optimization，PSO）的混合算法，用于确定BPNN（Back -propagation Neural Network，BPNN）和RF（Random Forest，RF）算法的最优超参数.基于某市地铁线路5个区间的实测数据，采用BPNN和RF算法分别建立地表最大沉降以及纵向沉降曲线的预测模型，并对两种机器学习算法的性能进行了对比分析.本文的研究对盾构掘进地表沉降预测及盾构掘进的智能控制有重要意义.

1沉降预测方法

1.1 BP神经网络

1.2随机森林算法

随机森林算法（RF）是一种基于决策树的集成学习算法，通常用于分类问题和回归问题. RF算法采用非参数计算，以随机的方式生成若干弱决策树，并通过集成所有决策树的预测结果进行预测. RF算法的随机主要体现在决策树生成的两方面：1）随机选取子样本；2）随机选取输入参数.该方式有效降低了决策树之间的相关性，使RF算法具有良好的鲁棒性和预测精度.

RF算法通过自主采样法（bootstrap sampling）和随机子空间方法进行构建，具体构建过程如下：

1）首先使用自主采样法，该方法模拟抽样统计推断法.在数据库中进行有放回的抽样，每一组数据被抽取的概率相同.随机抽取k个样本，得到数据库子集Ri.

2）从数据库子集Ri中随机选取m个特征（输入参数类别）作为随机森林的根节点，根据二叉树形式对Ri进行不断划分，从而构建生成CARF决策树.

3）依次重复以上步骤1）和步骤2），得到n个数据库子集，生成n个CARF决策树，从而组成随机森林.这些决策树可独立对输出目标做出预测，在分类问题中，最终结果通过投票方式产生；在回归问题中，最终结果为所有决策树的预测结果的平均值.

1.3粒子群算法

1.4基于粒子群算法优化的混合算法

超参数的选取决定机器学习算法的实际应用效果，其数值需要在机器学习模型训练前预先设置，多通过试错法确定一组较好的参数[10-11]，但该方法效率较低而且难以保证找到最优的参数.沉降预测模型中主要调整的超参数包括BPNN隐藏层节点数和RF算法的决策树棵数.本文基于PSO算法提出了确定两种机器学习算法最优超参数的混合算法，其中PSO算法中的粒子位置对应需要调节的超参数，适应度函数定义为模型在k折交叉验证集（cross-vali-dation，CV）上的预测误差.混合算法的流程如图1所示，具体步骤如下：

1）初始化粒子群，对粒子群的大小、粒子群的学习率、最大迭代次数进行赋值.粒子的初始位置和速度随机设定，粒子的位置代表BPNN的隐藏层节点数和RF算法的决策树个数.

3）PSO算法設定迭代次数，进行迭代时计算每一个粒子的适应度值，判断每次迭代后的适应度值是否达到目标数值或PSO算法的迭代次数是否达到最大值.若满足条件则停止迭代，优化过程停止，得到全局最优粒子位置，即机器学习算法的最优超参数.

1.6模型框架

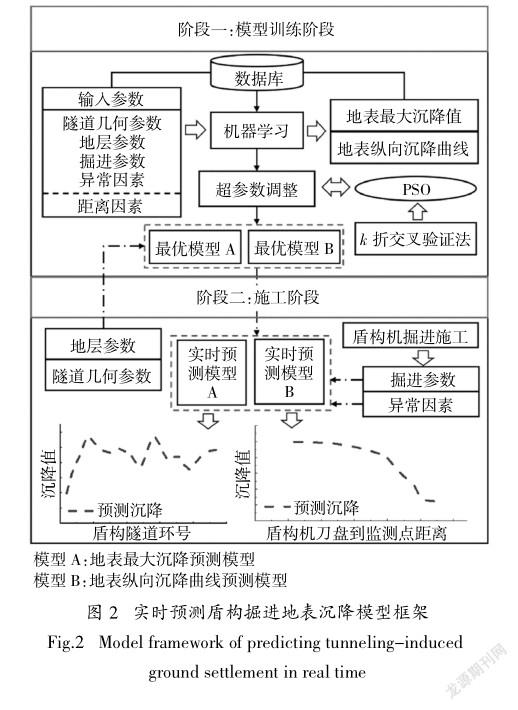
沉降预测模型的训练与预测过程独立进行，且预测计算时间较短，适用于实际工程中实时预测地表沉降.本文提出了用于盾构掘进过程中的沉降预测模型框架（如图2所示）.

具体实现步骤如下：

模型训练阶段：根据已有的数据库，并基于PSO混合算法调整机器学习算法的超参数，分别建立地表最大沉降预测模型（图示模型A）和地表纵向沉降预测模型（图示模型B）.

施工阶段：1）从盾构隧道沿线地勘报告中获取地质勘察结果，将地质条件转换为地质参数，并从隧道设计资料中获取隧道几何参数.这两类参数在施工过程中不会改变，故提前存储于沉降预测模型中；2）在盾构机的掘进过程中同步收集掘进参数，同时根据盾构机的掘进情况确定盾构异常因素；3）将盾构机每一环掘进产生的掘进参数和异常因素输入至预测模型A中，从而得到当前环号的地表最大沉降预测值.在输入参数中添加距离因素并导入预测模型B中，得到实时的地表纵向沉降的预测曲线.

2数据库建立

2.1数据源

数据来源于某市地铁线路6个地铁站5个区间，全长5.44 km，盾构隧道管片共计3 583环.隧道所处区域地质条件较为复杂，沿线地质剖面如图3所示.该区间内隧道均采用土压平衡盾构法施工完成.盾构机的长度为8.735 m，直径为6.28 m.管片衬砌外径为6 m，内径为5.4 m，采用错缝形式拼接.隧道左右线穿越的土层基本一致，穿越区域的覆土深度在10～28 m之间，地下水水位位于地表下约3 m位置处.

2.2输入参数选取

BPNN和RF算法预测地表沉降需要选取合理的输入参数，根据Zhang等[12]的研究，影响地表沉降的因素可以分为隧道几何参数、掘进参数、地质条件和异常因素四类.由于数据库中的隧道规格相同，而隧道的埋深与盾构掘进引起的沉降发展模式以及最终沉降的大小密切相关，且隧道埋深的大小随里程数不断改变，故盾构隧道的埋深作为唯一的隧道几何参数.盾构掘进参数选取与地层扰动程度相关的参数；推力、扭矩、土仓压力和贯入度，这些参数是盾构掘进控制的关键参数，并能通过盾构机数据采集系统实时采集，准确可靠.同时考虑到注浆量对盾构空隙以及后期沉降的较大影响[19]，所以该五个掘进参数被选为输入参数.输入参数选取的示意图如图4所示.

地质条件需考虑土层的基本物理力学性质以及土层的空间位置. Chen等[10]提出的地质参数的量化方法能综合考虑岩土层的物理力学性质以及空间位置信息，包括3个参数；修正标贯次数、修正动探次数、修正单轴抗压强度，故选为输入参数.此外，在开挖工作面或盾尾的地下水渗漏会引起孔隙水压力的降低并导致相应的固结沉降，渗漏量与地下空隙水压力有很大关系，所以地下水的深度选为输入参数.根据异常沉降点的统计分析，较大的地表沉降通常发生在盾构机开挖面为复合断面的位置，因此掌子面岩土层类型也作为一个输入参数.掌子面岩土层类型可分成四类；土体、圆砾和卵石、岩石以及复合面地层，分别编码为1、2、3、4.由于盾构机的停机可能导致地下水位的下降，从而引起地表沉降的变化，所以盾构机停机属于异常因素，1表示停机，0表示连续掘进.综上，12个参数选取为预测盾构掘进引起最大沉降预测模型的输入参数.对于预测纵向沉降预测曲线的模型，输入参数还包括盾构机刀盘与沉降监测点的距离，共计13个输入参数.所有数据以每一环为单位储存.同时，数据库中随机选取80%的数据作为训练集，剩余20%的数据作为测试集.

3预测结果

3.1超参数确定

在两种混合算法中，PSO算法对BPNN以及RF算法的超参数进行迭代更新.图5为混合算法中最优适应度值的变化过程.

在训练BPNN生成预测纵向沉降的模型时，适应度值没有变化，表明在粒子群初始化时生成该模型的最优超参数，且超参数的调整对该模型性能的提升不明显.在BPNN预测地表最大沉降的模型中，适应度值随迭代次数下降明显，该模型的性能有明显提升.总体来看，RF算法的两个预测模型的适应度值明显小于BPNN的适应度值.通过混合算法得到的最优超参数如表1所示.

3.2最大沉降预测结果

图6为BPNN的预测值与实际值的结果对比，可以发现训练集接近P = M直线，同时根据训练集两个评价指标；MAE = 2.58、R = 0.75，表明该模型训练集的学习效果较好.而测试集的结果中MAE较大，R较低，分别为4.25和0.32，说明模型在测试集上预测精度较低.并且随着实测沉降值的数值增加，预测精度明显下降.尤其在沉降值的最大点，预测值的误差较大.这是由于训练集数据中缺乏沉降值较大的数据，导致模型对较大沉降的预测存在较大的误差.

图7反映的是RF算法的预测结果，训练集两个性能评价指标的数值为：MAE=0，R=1，表明模型在训练集上表现优越.而测试集MAE和R的值分别为2.69，0.85，测试集的实测值与预测值差异较小，且相关性较好.即使在数据库中大的沉降数据较少的情况下，RF算法仍能准确地预测到较大的地表沉降，表明RF算法良好的泛化能力.

3.3縱向沉降曲线预测结果

BPNN预测纵向沉降的结果如图8所示.训练集的MAE值较高，达到了4.29，而相关系数R为0.72.同时，训练集中实测沉降值大于20 mm的预测值明显偏低，总体上学习效果一般.测试集的评价指标的数值与训练集相差不大，MAE和R分别为4.85、0.67，但表现出较差的预测性能.

图9反映的是RF算法预测纵向沉降中的结果.对于训练集，预测结果集中分布在P= M附近，MAE值较小，仅为1.15，相关系数R的值为0.98.对于测试集，性能评价指标的数值为MAE = 1.85、R = 0.80，预测结果也几乎在P= M直线附近上下波动，也能较为精确地预测大的沉降.

两种算法的纵向曲线预测结果如图10和图11，其中图10反映的是小（小于10 mm）的纵向曲线预测结果，图11则为大（大于10 mm）的纵向沉降曲线预测结果.

在图10中，BPNN的预测值在距离较小时与实际值较为符合，但预测的最终沉降值与实际值相差较大.在图11中，BPNN对最终沉降值的预测偏差较大. RF算法预测的沉降发展的位置、沉降发展的速度以及沉降最终的数值与实测结果一致，表明RF算法对不同情况下的纵向曲线预测均具有良好的性能.

3.4算法性能对比

两种机器学习算法的性能对比如图12和图13所示.对于训练集，BPNN的MAE明显高于RF算法，且R值小于RF算法，表明RF算法在训练集中的预测性能更好.对于测试集，BPNN和RF算法在最大地表沉降的预测中MAE差距不大，但RF算法的R明显更大.两种算法预测纵向沉降曲线时，RF算法的MAE远远小于BPNN，且R值更大.

4结论

本文提出了PSO算法与机器学习算法相结合的混合算法，该混合算法利用PSO算法确定BPNN和RF算法的最优超参数.同时综合考虑掘进参数、地质条件、隧道几何参数和异常因素对地表沉降的影响，提出了最大地表沉降和纵向沉降曲线的预测方法.最终通过某工程实测数据进行了对比分析.主要结论如下；

1）对盾构掘进引起地表最大沉降进行预测，BPNN和RF算法的绝对平均误差分别为4.24 mm、2.69 mm；对盾构掘进引起地表纵向沉降曲线进行预测，BPNN和RF算法的绝对平均误差分别为4.85 mm、1.85 mm.结果表明，BPNN沉降预测值与实际值相差较大，RF算法的预测结果误差较小.

2）BPNN和RF算法用于预测盾构掘进引起的地表沉降时，BPNN难以预测到较大的地表沉降，且在纵向沉降预测中对最终沉降的预测误差较大.RF算法在预测纵向沉降曲线时误差最小，能捕捉到盾构掘进过程中沉降的发展进程.因此，综合预测误差和预测效果，RF算法模型可作为盾构掘进引起的地表沉降的预测模型.

另外，本文的数据库来源仅限于某市的盾构隧道工程，地表沉降预测模型的性能可能由于地域差异存在不足，因此针对其他地区的盾构掘进地表沉降预测仍需进一步的验证.

参考文献

[1]ZHANG P，CHEN R P，WU H N，et al. Ground settlement induced by tunneling crossing interface of water-bearing mixed ground；a lesson from Changsha，China[J]. Tunnelling and Underground Space Technology，2020，96：103224.

[2]陳仁朋，张品，刘湛，等. MJS水平桩加固在盾构下穿既有隧道中应用研究[J].湖南大学学报（自然科学版），2018，45（7）：103—110. CHEN R P，ZHANG P，LIU Z，et al. Application study of MJS hori-zontal column reinforcement in shield tunneling[J]. Journal of Hu-nan University（Natural Sciences），2018，45（7）：103—110.（In Chinese）

[3]PECK R B. Deep excavations and tunneling in soft ground[C]// Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City，1969：225—290.

[4]陈春来，赵城丽，魏纲，等.基于Peck公式的双线盾构引起的土体沉降预测[J].岩土力学，2014，35（8）：2212—2218. CHEN C L，ZHAO C L，WEI G，et al. Prediction of soil settlement induced by double-line shield tunnel based on Peck formula[J]. Rock and Soil Mechanics，2014，35（8）：2212—2218.（In Chinese）

[5]魏纲，徐日庆.软土隧道盾构法施工引起的纵向地面变形预测[J].岩土工程学报，2005，27（9）：1077—1081.WEI G，XU R Q. Prediction of longitudinal ground deformation due to tunnel construction with shield in soft soil[J]. Chinese Journal of Geotechnical Engineering，2005，27（9）：1077—1081.（In Chinese）

[6]刘元雪，施建勇，许江，等.盾构法隧道施工数值模拟[J].岩土工程学报，2004，26（2）：239—243. LIU Y X，SHI J Y，XU J，et al. Numerical simulation of excavation of shield tunnel[J]. Chinese Journal of Geotechnical Engineering，2004，26（2）：239—243.（In Chinese）

[7]朱才辉，李宁，柳厚祥，等.盾构施工工艺诱发地表沉降规律浅析[J].岩土力学，2011，32（1）：158—164. ZHU C H，LI N，LIU H X，et al. Analysis of ground settlement in-duced by workmanship of shield tunnelling[J]. Rock and Soil Me-chanics，2011，32（1）：158—164.（In Chinese）

[8]徐前卫，朱合华，廖少明，等.软土地层土压平衡盾构法施工的模型试验研究[J].岩土工程学报，2007，29（12）：1849—1857. XU Q W，ZHU H H，LIAO S M，et al. Experimental study on EPB shield tunnel construction in soft ground[J]. Chinese Journal of GeotechnicalEngineering，2007，29（12）：1849—1857.（InChinese）

[9]孙钧，袁金荣.盾构施工扰动与地层移动及其智能神经网络预测[J].岩土工程学报，2001，23（3）：261—267. SUN J，YUAN J R. Soil disturbance and ground movement under shield tunnelling and its intelligent prediction by using ANN tech-nology[J]. Chinese Journal of Geotechnical Engineering，2001，23（3）：261—267.（In Chinese）

[10]CHEN R P，ZHANG P，KANG X，et al. Prediction of maximum sur-face settlement caused by earth pressure balance（EPB）shield tun-neling with ANN methods[J]. Soils and Foundations，2019，59（2）：284—295.

[11]CHEN R P，ZHANG P，WU H N，et al. Prediction of shield tunnel-ing-induced ground settlement using machine learning techniques[J]. Frontiers of Structural and Civil Engineering，2019，13（6）：1363—1378.

[12]ZHANG P，CHEN R P，WU H N. Real-time analysis and regulation of EPB shield steering using Random Forest[J]. Automation in Construction，2019，106：102860.

[13]SHI J S，ORTIGAO J A R，BAI J L. Modular neural networks for predicting settlements during tunneling[J]. Journal of Geotechnical and Geoenvironmental Engineering，1998，124（5）：389—395.

[14]SANTOS O J Jr，CELESTINO T B Jr. Artificial neural networks analysis of Sao Paulo subway tunnel settlement data[J]. Tunnelling and Underground Space Technology，2008，23（5）：481—491.

[15]AHANGARI K，MOEINOSSADAT S R，BEHNIA D. Estimation of tunnelling-induced settlement by modern intelligent methods[J]. Soils and Foundations，2015，55（4）：737—748.

[16]WANG F，GOU B C，QIN Y W. Modeling tunneling-induced ground surface se ttlement development using a wavelet smooth relevance vectormachine[J].ComputersandGeotechnics，2013，54：125—132.

[17]ZHOU J，SHI X Z，DU K，et al. Feasibility of random-forest ap-proach for prediction of ground settlements induced by the construc-tion of a shield-driven tunnel[J]. International Journal of Geome-chanics，2017，17（6）：04016129.

[18]KOHAVI R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]// International Joint Conference on Artificial Intelligence. Montreal：Morgan Kaufmann Publishers Inc，1995：1137—1145.

[19]馬文辉，杨成永，彭华，等.大直径泥水盾构下穿地铁挡墙路基沉降控制[J].湖南大学学报（自然科学版），2020，47（3）：44—53. MA W H，YANG C Y，PENG H，et al. Settlement control on retain-ing wall embankment affected by underneath traversing large-diam-eter slurry shield tunnels[J]. Journal of Hunan University（Natural Sciences），2020，47（3）：44—53.（In Chinese）