正定矩阵三类典型的构造方法及其相关原理
2021-02-08 07:37:58东华理工大学理学院胡康秀
内江科技 2021年1期
◇东华理工大学理学院 胡康秀 丁 云 杨 扬 魏 艳
正定矩阵是从二次型的正定性中抽象出来的一个概念,由于其良好的性能,使其不仅在代数学中有着广泛应用,同时在函数学、几何学、图像处理学、概率统计和物理学等其他学科中也都有很好的拓展。本文主要从几个不同的角度探讨正定矩阵的构造方法,并给出相应的理论原理。
1 引言
在数学的学习过程中,往往侧重于对数学概念的熟悉、相关性质的理解以及对解题方法的掌握,而运用数学原理中构造性思维进行创新训练不多。正定矩阵是一类非常特殊的矩阵,作为对称矩阵的子类,除了具备对称矩阵可对角化的性能之外,在矩阵分解理论中也有很好的的结论。大家在高等代数学习的过程中关注的更多的是正定矩阵的性质和应用,但是如何构造满足需求的特殊的正定矩阵也值得大家思考与探究。本文从矩阵运算的角度入手,利用相关性质,从三个方面探究正定矩阵的构造思路及方法。
2 对称矩阵的几点性质
因为正定矩阵属于对称矩阵的范畴,为构造正定矩阵,下面分别从一般矩阵和对称矩阵的角度探究对称矩阵的构造方法。依据【性质1】可以由一般矩阵构造出对称矩阵。
如果想在已有对称矩阵的基础上构造出新的对称矩阵,那么则下面两条性质是很好的思路和启发。
接下来从矩阵元素、矩阵运算及特征值等三个角度分别给出正定矩阵的构造方法。
3 对称矩阵的三种典型的构造方法
(1)元素构造法:从矩阵内部元素从发,通过选取特殊的数来构造满足特定需要的正定矩阵。

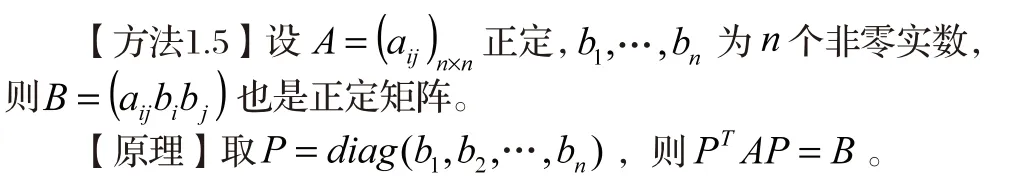
(2)矩阵运算构造法:通过矩阵各类运算组合构造出满足特定需要的正定矩阵。
(3)特征值构造法:特征值是正定矩阵一个非常直观的属性,依据矩阵运算特征值相关的性质来构造出满足特定需要的正定矩阵。

4 结语
本文仅仅在数学理论的基础上探究了正定矩阵的三类典型的构造方法,在实际应用中,要结合不同学科背景以及具体研究目标综合运用。
猜你喜欢
电工技术学报(2023年20期)2023-10-31 08:09:26
小学生作文(低年级适用)(2022年10期)2022-10-31 01:51:28
中学生数理化·七年级数学人教版(2022年11期)2022-02-14 07:13:52
数学物理学报(2021年5期)2021-11-19 07:01:12
烟台大学学报(自然科学与工程版)(2021年1期)2021-03-19 08:38:40
现代临床医学(2021年1期)2021-01-26 00:56:32
咸阳师范学院学报(2016年6期)2017-01-15 14:18:38
厦门理工学院学报(2016年1期)2016-12-01 04:50:52
东北电力大学学报(2015年1期)2015-11-13 05:20:25
四川轻化工大学学报(自然科学版)(2014年3期)2014-04-16 03:56:42

