大激活熵是触发非晶合金记忆效应的关键＊

宋丽建，许巍，霍军涛，王军强

中国科学院宁波材料技术与工程研究所，浙江 宁波 315201

生活中，人类可以寻找到多种记忆形式，如结绳记事、文字记载和影像记录等鲜活永恒的形式，但也有些记忆形式并不容易触动，如非晶态材料在能量驱动下会发生的自然“老化”过程。然而，1963年美国威斯康星麦迪逊大学的Kovacs教授[1]发现：非晶态材料如果经过先低温再高温两步退火过程，它的体积或焓不是单调“老化”，而是先升高再降低。这种反常的焓升高引起的“年轻化”现象被称为Kovacs记忆效应。这种两步退火方式可以实现铁基非晶合金软磁性能的进一步优化[2]。

唯象理论模型，如Tool-Narayanaswamy-Moynihan（TNM）模型[3-5]，认为记忆效应起源于玻璃的不均匀性结构，通过调节模型中玻璃的两个虚拟温度之比可以定性地拟合玻璃的记忆效应。实验结果也表明，记忆效应与玻璃动力学不均匀性具有一定的关联性[6-7]。然而，TNM模型仅可以描述高分子玻璃和氧化物玻璃等各种热激活体系[8-9]，并不适用于褶皱纸团、摩擦表面、颗粒材料等非热激活体系[10-14]。作为一种普适性物理现象，记忆效应不受化学成分、化学键以及相互作用形式等的影响。寻找可以表征记忆效应的普适性物理量，对认识记忆效应演化规律和机制，从而改善合金性能和优化热处理工艺具有重要意义。

1 非晶合金中弛豫动力学

熔体快速降温过程中，原子运动能力会在某一温度处骤减，此时熔体的体积或焓发生转变，熔体被冻结成非晶。虽然非晶保留了液体的结构特征，却不具备液体的各态遍历特性，而表现出丰富的弛豫模式。按照特征频率由低到高，驰豫模式可以分为α弛豫、β弛豫、玻色峰弛豫和双能级弛豫等。其中，α弛豫被认为是多数原子的大尺度协同运动，弛豫频率低；β弛豫则是局域的原子重排过程，弛豫频率高（图1）[15-16]。

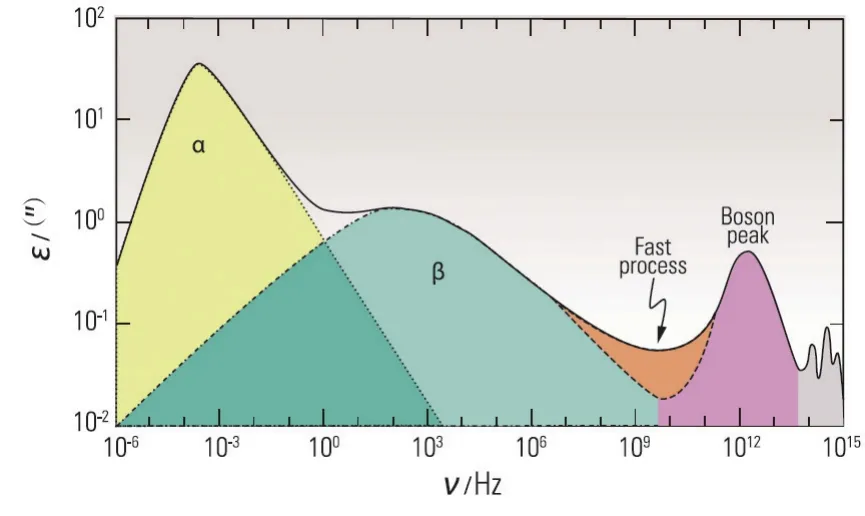
图1 非晶材料的动力系弛豫谱[15]

非晶态中，α弛豫已经被冻结，β弛豫是主要存在模式。β弛豫具有过剩尾、肩膀型和显著的峰型等多种表现形式[15]，这与非晶合金的力学、磁学等性质具有密切联系[17-19]。在工业应用中，人们发现具有明显β弛豫峰的材料，其拉拔温度可以选在β弛豫与α弛豫温度之间。降低拉拔温度可节约能源和成本[20]，因此从弛豫动力学角度理解材料性质具有重要意义。

2 非晶合金退火弛豫转变行为

由于能量状态可调，非晶合金在实际应用过程中，一般需要先进行退火弛豫处理以改善性能。退火弛豫主要涉及非晶合金的β弛豫和α弛豫等不同弛豫模式。为了明确等温退火过程中的弛豫演化规律，我们使用高精度闪速差示扫描量热仪（Flash DSC 1），以低熔点、抗氧化、玻璃形成能力好的Au基非晶合金Au49Cu26.9Ag5.5Pd2.3Si116.3(原子百分比)为模型，进行系统研究。

单步等温退火过程：非晶合金样品先在液相线温度以上充分熔化，然后以Rc=10 000 K/s的降温速率迅速降温至退火温度（Ta）进行不同时间（ta）退火处理；退火完成后仍以Rc=10 000 K/s的降温速率降至183 K或室温，最后以Rh=100、200、500、1 000 K/s的升温速率测量退火后样品的热流曲线（图2）[21]。相比于淬态非晶合金样品，非晶合金在Ta=363 K退火ta=0.1 s后，其在升温过程中会出现一个明显的吸热峰（图2（b））。据此构建的弛豫峰随温度和退火时间演化的二维轮廓图（图2（c））可以看出，弛豫峰峰值温度（Tp）随退火时间的演化不是单一的，而是存在两个演化阶段：在短时间退火阶段，Tp迅速增加；随着退火时间的增加，Tp进入缓慢增加阶段。

图2 （a）非晶合金退火方案示意图；（b）淬态和弛豫后非晶合金的DSC热流曲线（插图为两条热流曲线相减得到的弛豫峰，Rh=500 K/s，Ta=363 K，ta=0.1 s）；（c）弛豫峰随温度和时间演化的二维等高线图[21]

为了明确等温退火中的弛豫动力学过程，我们给出样品弛豫峰随升温速率的变化关系（图3（a））。可以看出，Tp随着升温速率的增加逐渐向高温方向移动，且这种温度-升温速率依赖性符合Kissinger关系[22-23]。通过Kissinger方法拟合不同退火时间弛豫峰随升温速率的变化斜率，并获得不同弛豫状态的激活能E*（图3（b））。随着退火时间的增加，拟合斜率逐渐增加并最终趋于定值，说明激活能随退火时间的变化存在转变过程。图3（c）给出激活能与退火时间的演化关系。在初始退火阶段，激活能较小且基本保持一个常数（75～95 kJ/mol）；当退火时间足够长时，激活能逐渐增大并最终趋于定值（160～175 kJ/mol）。激活能的转变时间与弛豫峰峰值温度的转变时间保持一致，证明退火过程中存在两步弛豫现象。进一步的研究发现，初始退火阶段的激活能约为（25.5±2）RTg（R为气体常数，Tg=401 K是在升温速率为0.33 K/s时测量得到的玻璃转变起始温度[24]），与β弛豫激活能（Eβ≈26RTg）相当。第二个退火阶段的激活能约为（50±2）RTg。考虑到弛豫峰峰值温度Tp=450 K（Ta=363 K，保温时间ta=1 000 s，1 000 K/s升温速率测量）远大于玻璃转变温度（Tg=401 K）以及α弛豫的非Arrhenius特征，第二阶段的激活能近似等于α弛豫的激活能。此外，β弛豫向α弛豫的转变时间（tβ-α）具有很强的温度依赖性，随着退火温度的升高而缩短，说明β弛豫向α弛豫的转变过程是一个热激活过程。激活能演化的三维轮廓图（图3（d））可以更好地揭示激活能随退火温度和时间的演化，低温短时间退火经历β弛豫阶段，而高温长时间退火触发α弛豫阶段[21]。这一结果为精准调控非晶合金的等温退火过程奠定了理论基础。

图3 （a）热流弛豫峰随升温速率的变化关系；（b）不同退火时间下峰值温度Tp的Kissinger关系；（c）激活能对退火时间的依赖关系；（d）不同退火温度和不同退火时间下激活能演化的三维等高线图[21]

3 非晶合金的记忆效应

现有研究表明，记忆效应是一种具有普适性的现象，与材料的化学键性质没有明显关系。在非晶合金中，增加第一步低温退火时间，可以显著提高记忆效应的强度[6]，甚至如果对非晶材料进行“训练”，将第二步高温退火过程分解成多个中间温度退火，记忆效应也会得到显著增加[25]。目前，有关非晶合金弛豫状态的研究主要集中在焓和激活能上，而对弛豫熵变特征却少有研究。事实上，熵反映了物质的微观状态数，对非晶的玻璃形成能力、磁热功能特性等其他重要性质都有重要影响[26-28]。因此，熵或许可以为理解记忆效应提供理论依据。

首先，我们对比分析了单步和双步退火过程中的焓弛豫过程。样品在Ta=383 K的等温退火过程中，焓随着退火时间的增加逐渐降低，并最终进入到亚稳平衡态（图4（a））[29]。同样地，弛豫峰随退火时间单调增加，且弛豫峰峰值温度向高温方向移动（图4（d））。其次，如果样品先在T1=383 K退火50 s，然后迅速降温至T2=373 K进行等温退火处理，焓随时间的演化仍是逐渐降低并最终趋于恒定，而且弛豫峰随时间的演化也是单调的（图4（b、e））。最后，如果样品先在T1=373 K退火50 s，然后迅速升温至T2=383 K进行等温退火处理，焓随时间不再是单调衰减，而是先随退火时间增加而增加后随时间降低至平衡态。从弛豫峰中也可以看出，弛豫峰强度也存在先降低后增加的趋势（图4（c、f ））。也就是说，预退火处理造成热历史的区别并不一定会激活记忆效应，还依赖于初始退火温度。如果第一步预退火温度高于第二步退火温度，则不会出现记忆效应；如果第一步预退火温度低于第二步退火温度，则出现记忆效应。

图4 （a）单步等温退火中焓随退火时间的变化关系（Ta=383 K，插图为退火方案）；（b）先高温后低温退火中焓随退火时间的变化关系（T1=383 K，T2=373 K，t1=50 s，t2=0.1～100 000 s，插图为退火方案）；（c）先低温后高温退火中焓随退火时间的变化关系（T1=373 K，T2=383 K，t1=50 s，t2=0.1～2 000 s，插图为退火方案）；（d）单步等温退火中弛豫峰随时间演化的二维轮廓图；（e）先高温后低温退火中弛豫峰随时间演化的二维轮廓图；（f）先低温后高温退火中弛豫峰随时间演化的二维轮廓图[29]

固定第二步退火温度（T2=383 K），改变第一步预退火温度（T1=348、363、373 K），对比分析预退火条件对记忆效应的影响（图5（a～c））。在可测量的时间范围内，预退火时间非常短时，弛豫焓随时间单调衰减；而当预退火时间足够长时，可以激活记忆效应。此外，对于相同的预退火时间，比如t1=100 s，焓回复到最大值所需时间随预退火温度的升高而增加。这说明记忆效应不仅依赖于预退火温度，还依赖预退火时间。也就是说，非晶合金先在低温进行预退火，然后升温至高温退火，并不一定激活记忆效应，只有预退火达到一定状态时第二步退火才会出现记忆效应。并且，记忆效应随着预退火时间的增加而增强，回复至最大值的时间也会随之增加。

TNM模型可以描述非晶合金等温退火过程中焓和体积随时间演化的非指数特征。在单步退火条件下，虚拟温度随时间的变化可以表示为[5]：

其中，Tf为虚拟温度，β是非指数参数，A是一个常数，x是非线性参数，τa是弛豫时间，H*是激活焓。TNM模型给出不同预退火条件下的焓变规律(拟合参数H*=164 kJ/mol，A=6×10-22s，=0.6，β=0.43，图4（c）的拟合曲线也由该参数获得的)，该模型虽然可以定性描述记忆效应的出现，但不能很好地描述记忆效应的演化规律。图5（d）给出了记忆效应强度Δhpeak（Δhpeak由峰值焓变减去初始焓变所得)随预退火焓变的影响关系。在预退火焓变Δh＜0.4 kJ/mol时，记忆效应会迅速衰减，表明当非晶合金焓进入深度弛豫阶段时，记忆效应才可以探测到。

图5 两步退火条件下的焓随时间的演化关系：（a）T1=348 K，t1=0.1～100 s；（b）T1=363 K，t1=0.1～100 s；（c）T1=373 K，t1=0.1～100 s；（d）记忆效应强度与预退火焓变关系（虚线为引导线）[29]

Cagle等人[30]在1951年引入绝对反应速率理论来理解晶态和非晶态材料的应力退火弛豫过程，进一步获得在差热分析中的应用：

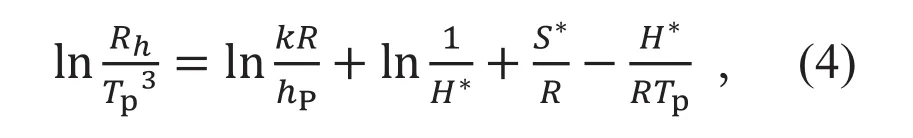
其中，κ是玻尔兹曼常数，hP是普朗克常数，R是气体常数，H*和S*分别代表激活焓和激活熵。方程（4）可以很好地描述Tp对升温速率的依赖关系，并根据拟合的斜率和截距获取不同弛豫状态下的激活焓和激活熵。图6（a）所示，短退火时间阶段的激活焓H*约为90 kJ/mol，随着退火时间的增加逐渐增加到约150 kJ/mol。相比于H*，激活熵S*变化更剧烈，即短时间退火阶段的S*接近于0（约15 J·mol-1·K-1），随着退火时间的增加，S*增加到约150 J·mol-1·K-1（图6（b））。这一结果表明，长时间退火伴随着显著熵变过程，存在更多跳转初始态的路径。

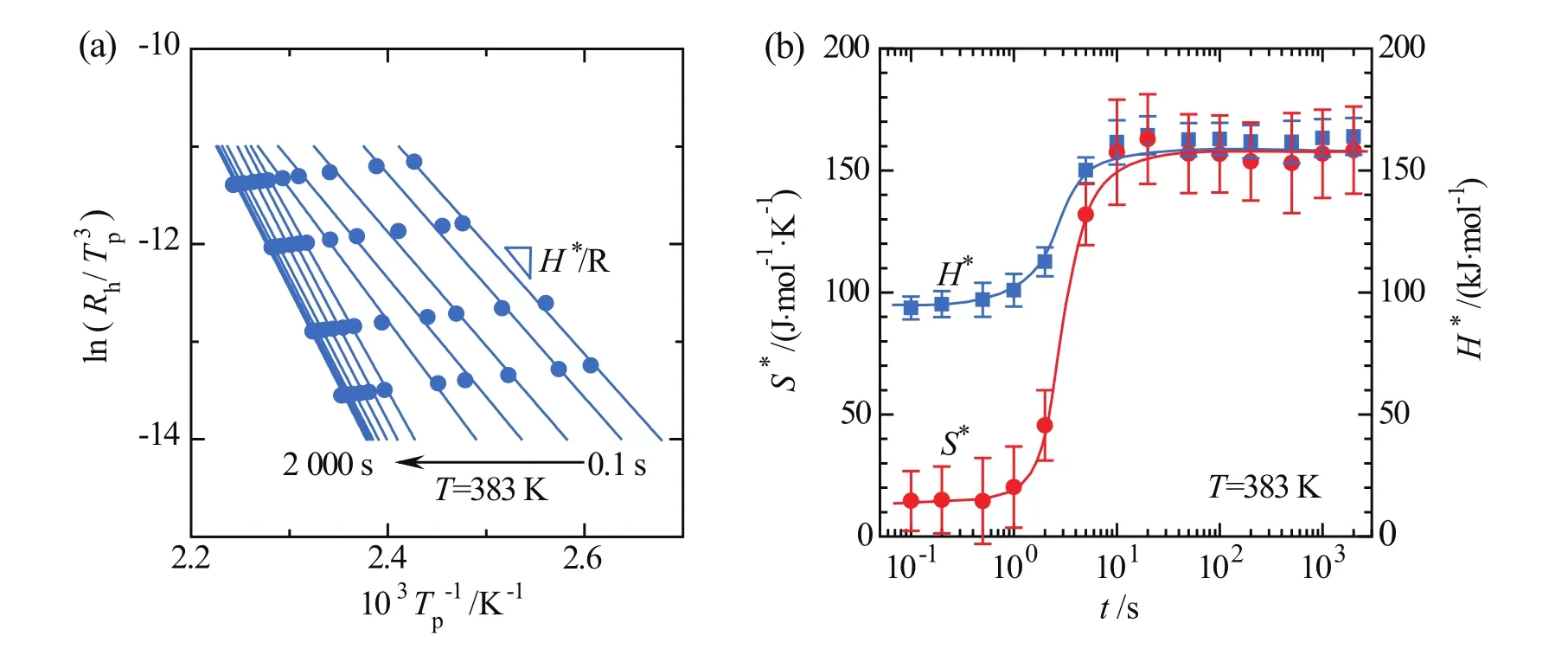
图6 （a）弛豫峰随升温速率的变化关系；（b）激活焓和激活熵与时间的演化规律[29]

我们进一步给出T=348、363、373、383 K时，等温退火过程中激活熵S*随弛豫焓的变化关系。如图7（a）所示，图中粉色箭头表示引起记忆效应的温度跳变过程，与图5（a）的粉色数据保持一致。这些结果表明，从低温跳向高温时，只有当高温退火阶段的激活熵比较大时，才会出现记忆效应。激活熵小时，则无法探测到记忆效应。大的激活熵意味着材料在弛豫过程中存在更多的演化路径。在低温退火弛豫阶段，焓随时间逐渐降低。当从低温跳转到高温进行等温退火处理时，如果跃迁至小激活熵的弛豫阶段，则不会出现记忆效应。反之，如果跃迁至大激活熵的弛豫阶段，就会出现记忆效应（图7（b））。虽然这些结果是基于非晶合金这样的热激活无序体系发现的，但由于熵的概念适用于所有无序复杂系统，因此相关结论对理解非热激活体系中的记忆效应也有帮助[29]。

图7 （a）单步退火中激活熵与焓变的关系；（b）焓空间中激活记忆效应的示意图[29]

4 总结

非晶合金因其原子结构无序、能量状态可调，而具有丰富的弛豫动力学过程。对等温退火弛豫规律的研究一直是人们关注的前沿科学问题。以往人们普遍认为等温退火属于单一动力学过程，但我们的研究结果表明等温退火并不是单一过程，而是存在从β弛豫动力学向α弛豫动力学转变的现象。而且，我们进一步发现，如果进行先低温再高温两步退火时，当进入深度弛豫状态（弛豫焓变足够大），将会出现记忆效应，这与深度弛豫α弛豫阶段的大激活熵密切相关，说明大激活熵是触发记忆效应的关键。相关结论对改善材料性能、优化热处理工艺以及认识非晶态材料的热稳定性和非晶态本质具有指导意义。