气轨法验证动量守恒定律实验中影响因素的探讨

欧阳建伟

(深圳市翠园中学 广东 深圳 518001)

在用气垫导轨来验证动量守恒实验过程中发现光电门位置，以及两滑块的质量，导轨调平等因素对实验的结果有不小的影响，为此，有不少学者进行了一些研究.陈皓等从气垫层的内摩擦力、平均速度代替瞬时速度以及气垫导轨调平等方面对实验中容易出现系统误差的几个方面进行了分析[1].邹力勋认为在气垫导轨实验中主要有光电门结构稳定性以及光路安排、滑块速度、气压等几方面的影响[2].但这些因素在验证动量守恒定律实验时，对测量结果的影响如何，以及如何选择实验条件，这些条件在实验中如何去满足，则需要进行实验来研究.本文以验证动量守恒定律为例，从实验测量的角度分析这些因素对实验的影响，这一研究对用气垫导轨验证动量守恒定律实验具有一定的指导意义.

1 实验原理

如果一个力学系统所受的合外力为零或在某方向上的合外力为零，则该力学系统总动量守恒或在某方向上守恒[3].如图1所示，设滑块1和2的质量分别为m1和m2，碰撞前两个滑块的速度分别为v10和v20，碰撞后的速度分别为v1和v2，则根据动量守恒定律有

m1v10+m2v20=m1v1+m2v2

(1)

图1 验证动量守恒定律实验原理示意图

1.1 完全弹性碰撞

完全弹性碰撞是一种理想的碰撞，其特点是碰撞前后不仅系统的动量守恒，且机械能也守恒.如果在两个滑块的相碰端都安装上弹性的缓冲弹簧，则滑块之间发生对心碰撞时，有

(2)

如果令v20= 0，则动量损失率P为

(3)

动能损失率E为

(4)

理论上，完全弹性碰撞的动量损失和能量损失都为零.但在实验过程中，由于空气阻力和气垫导轨本身的原因，是不可能完全为零.

1.2 完全非弹性碰撞

如果两个滑块碰撞后，以同一速度运动而不分开，就称为完全非弹性碰撞.其特点是：碰撞前后系统的动量守恒，但机械能不守恒，实验室中为了较好地实现完全非弹性碰撞，可以在滑块相碰端装上尼龙搭扣或放置黄油.则有

m1v10+m2v20=(m1+m2)v

(5)

在实验中，让v20= 0，则动量损失率P为

(6)

动能损失率E为

(7)

1.3 碰撞恢复系数

牛顿曾提出“弹性恢复系数”的概念，一般称为恢复系数，用e表示，其定义为:对于材料一定的两物体,碰撞后分开的相对速度与碰撞之前接近的相对速度成正比[4].碰撞前接近时的相对速度为v10-v20，碰后分离时的相对速度v2-v1，于是就有

(8)

恢复系数e由碰撞物体的材质决定，e值可由实验来测定，滑块上的碰撞弹簧是钢制的，e值在0.95～0.98，虽然它接近1，但是其差异也是明显的，因此,在实际的气垫导轨上是不能实现理想的完全弹性碰撞的.

2 测量仪器及测量过程

2.1 测量仪器

气垫导轨(L-QG-T-2000/5.8),计时计数测速仪(MUJ-5C),滑块,尼龙搭扣,配重块,挡光片,光电门,游标卡尺,数字天平等.

2.2 测量过程

(1)完全弹性碰撞

接通电源，并将导轨调至水平，取两滑块m1和m2，并给两滑块都装上宽度为3 cm的U型挡光片[5]，再给两滑块分别安装上弹簧钢圈，并用电子秤称出m1和m2的质量(包括挡光片及碰簧)，将滑块m2置于两光电门的中间，并使其静止，再将另一个滑块m1放在光电门G1的外侧，用一外力使滑块m1朝滑块m2方向运动并与m2做对心碰撞，分别记下m1通过两个光电门的时间Δt0和Δt1，以及m2通过第二个光电门的时间Δt2，重复实验5次，记录所测数据，计算E和P,并分析误差产生的原因.

(2)完全非弹性碰撞

导轨调平后，对于两个滑块m1和m2，只需要给滑块m1安装上宽度为3 cm的U型挡光片，而滑块m2不需要安装挡光片[6]，再将两滑块碰撞的一端分别安装上尼龙搭扣，用电子秤称出m1，m2的质量(包括挡光片及尼龙搭扣)，将滑块m2置于两光电门之间，使其静止，将另一个滑块m1放在光电门G1的外侧，用一外力使滑块m1朝滑块m2方向运动并与m2做对心碰撞，分别记下滑块m1通过光电门的时间Δt0，以及m1,m2粘在一起后通过第二个光电门的时间Δt2，重复实验5次，记录所测数据，计算E,P，并分析误差产生的原因.

3 测量结果与分析

3.1 完全弹性碰撞实验中两光电门间的距离对测量的影响

在验证完全弹性碰撞的实验中，测量得m1=331.72 g,m2= 174.21 g，挡光片的宽度为0.03 m.因为两滑块自身有一定的长度，两滑块上的两光电门之间最小距离为34 cm，而本次实验需要两滑块所载的挡光片在碰撞时应在两光电门之间的距离内方能进行有效测量.实验时保持m2位置不变，设滑块m2上的挡光片后沿距光电门G2的距离为S2，通过移动光电门G2的位置来改变两光电门的距离，并以此来探究其对实验测量结果的影响.实验测量结果如表1所示.

表1 当滑块m1 > m2时两光电门之间的距离变化对测量结果的影响

从表1中可以看出，除部分数据点存在实验操作误差外，碰撞系数均较高，说明两滑块的碰撞也是比较接近完全弹性碰撞.在S2>7 cm时，动量损失率和能量损失率随着两光电门之间距离的增大而有所减小.但在实验中我们发现，当S2< 2 cm，即m2上的挡光片离光电门G2非常近时，例如当S2为0.5 cm时，动量损失率超过12%，能量损失率则超过30%，此时实验误差已经非常大，通过反复观察实验过程，发现两个碰簧在碰撞的极短时间内是处于压缩并接触状态的，而此时滑块m2上的挡光片如果初始就离光电门G2非常近，就相当于在碰撞的瞬间就已经开始计时，而并不是实验原理所要求的碰撞完后开始计时.这就导致测量出的Δt2变小，实验误差变大.而当S2比较大时，发现实验误差又有所增大，有时还会出现动量损失为负值的情况，除了部分实验过程中出现操作上的失误外，我们认为还有可能的原因是导轨中后段局部存在弯曲不平直的原因而导致的.

随着两光电门之间距离的变化，m2在两光电门之间位置也在发生变化，即碰撞点相对于时间测量点也在随之改变.那么m2在两光电门之间位置的不同对测量结果有没有影响呢？为此我们设计实验，让两光电门间距离为55 cm不变，使刚好可以碰撞的点距G1光电门的距离S1等于5 cm，通过改变滑块m2在两光电门之间的位置来探究其对测量结果的影响.得出的实验结论与上个实验是基本一致的.所以在实验过程中，需要选择合适的光电门之间的距离以及滑块的位置.实验中，选择两光电门之间的距离为45 cm，S2等于6 cm左右时，实验误差已经比较小，在误差允许范围内，可以认为完全弹性碰撞实验得以实现.

3.2 完全弹性碰撞实验中两滑块质量变化对测量的影响

我们认为两滑块质量的不同可能也会对实验的测量造成一定的影响，为了验证我们的猜想，我们在上一个实验的基础上，令m1= 331.72 g，两光电门之间的距离为45 cm，S2等于6 cm，通过改变滑块m2的质量，测量其结果如表2所示.

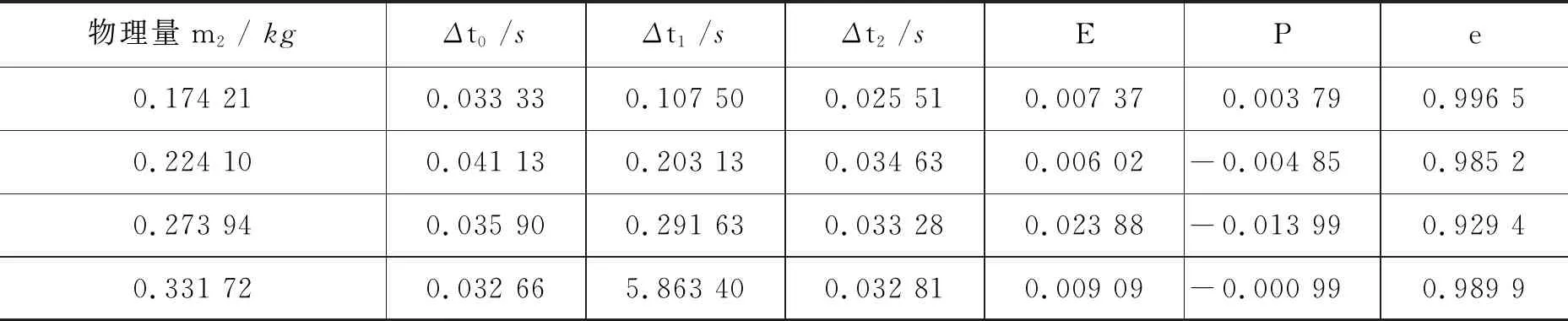
表2 当滑块质量m1 > m2时m2质量的变化对测量结果的影响

为了探究当滑块m1

表3 当滑块质量m1 < m2时m1质量的变化对测量结果的影响

从表2和表3中可以看出，随着滑块质量的改变，实验结果没有很明显的变化，而且实验误差也都不大，在误差允许范围内，可以认为两物体发生了完全弹性碰撞.值得注意的是，当m1=m2= 331.72 g时，两滑块碰撞后，滑块m1的速度几乎为零，相当于彼此交换了速度.为了实验的精确性，建议在验证动量守恒实验中，选择滑块m1的质量略大于滑块m2时，有不错的实验效果.

3.3 完全非弹性碰撞中光电门位置及滑块质量对测量的影响

在对完全弹性碰撞实验的影响因素进行探讨之后，我们想到对完全非弹性碰撞实验中这些因素是否也一样影响着实验呢?之前的实验中研究光电门位置时是通过改变光电门的距离，在完全非弹性碰撞实验中，只有一个滑块上的挡光片需要遮光计时，为此我们设计实验，取6个光电门在导轨每隔10 cm的位置安装一个.为方便读数应依次安装在两台计时器上，将滑块m2放置在第一、二个光电门之间，测得滑块m1= 334.72 g保持不变，通过改变滑块m2的质量进行实验，从而来探究光电门的位置及滑块质量对测量结果的影响.

动量损失率P、能量损失率E随两光电门之间距离变化的实验结果如2图所示.

图2 动量损失率P、能量损失率E随两光电门之间距离变化的关系图

从图2中可以看出，在完全非弹性碰撞实验中动量损失率随着两光电门之间距离的增大有着近乎线性增大趋势，当选择两光电门间的距离为10 cm时，动量损失率基本都在0.6%以下，而当两光电门间的距离为50 cm时，动量损失率则达到1.5%左右.而能量损失率则随两光电门间的距离的改变而变化不是太大.因此我们认为在实验过程中，需要选择合适的两光电门的距离.

动量损失率P、能量损失率E随滑块m2质量变化的实验结果如图3所示.从图3可以看出，当m1>m2时，动量的损失率随着滑块m2质量的增大有减小的趋势；而在m1

图3 动量损失率P、能量损失率E随滑块m2质量变化的关系图

4 结论

本实验研究了两光电门之间的距离和滑块质量的不同在验证动量守恒中的完全弹性碰撞和完全非弹性碰撞两种碰撞类型实验中的影响.

从总体来看，在验证完全弹性碰撞实验中，当S2< 6 cm时，误差随两光电门之间距离的增大而有所减小，当S2< 2 cm，即m2上的挡光片离光电门G2非常近时，实验误差非常大.对于S1距离的探讨同样有相似的结论，其根本原因是此时碰撞过程已经不在计时区内了.随着滑块质量的改变，实验结果没有很明显的变化，而且实验误差也都不大，我们认为在这个实验中，需要选择合适的光电门之间的距离以及滑块的位置.选择两光电门之间的距离为45 cm，S2为6 cm左右，选择滑块m1的质量略大于滑块m2时，有不错的实验效果.

在验证完全非弹性碰撞实验中，动量损失率随两光电门之间距离的增大有近乎线性增大的趋势，而动能损失率则变化不大.当m1>m2时，动量的损失率随着滑块m2质量的增大有减小的趋势；而在m1