基于集成学习的骨质疏松性骨折预测研究
陈婉琦,林勇
上海理工大学医疗器械与食品学院,上海200093
前言
骨质疏松症是骨骼的主要疾病,其特征是骨密度降低和骨组织微结构损坏,进而导致骨折敏感性增加[1]。由骨质疏松症引起的骨折叫骨质疏松性骨折,其给患者带来巨大痛苦,并给社会和医疗系统带来沉重负担[2]。骨质疏松症的发病率在女性中最高,但在接下来的50年中,男性的发病率有可能会翻3倍[3]。因此根据临床变量预测男性骨质疏松性骨折风险对其预防至关重要。
近年来机器学习在医学领域的应用越来越广泛,出现了基于机器学习的骨质疏松性骨折预测研究。章轶立等[4]通 过Group Lasso 回归算法和Logistic回归模型初步构建骨质疏松性骨折风险评估工具。Villamor等[5]结合临床和生物力学数据通过支持向量机(Support Vector Machine,SVM)对髋部骨折进行有效预测。此类单一模型的预测精度仍有较大提升空间,进而有研究提出采用集成学习方法提高模型预测性能。Kruse 等[6]使用逻辑回归、随机森林模型以及Bagging 和Boosting 集成学习方法预测髋部骨折,研究结果表明集成学习方法预测效果更佳。Kilic 等[7]使用 Bagging、梯度提升(Gradient Boosting)、随机子空间(Random Subspace)采样等集成学习方法对绝经后妇女进行骨质疏松性骨折预测,结果显示基于随机子空间的随机森林(Random Forest based on Random Subspace, RSM-RF)集成分类器模型预测精度最佳。目前使用集成学习模型的研究绝大多数是对相同结构的个体学习器进行集成,使用异构分类器的研究还相对较少。
本研究使用学习法的典型代表Stacking 构建异构分类器EtDtb-S,经相关性分析后筛选出16 个特征作为特征向量,选用极端随机树、基于决策树的Bagging 集成模型(Decision Tree Based on Bagging,DTB)作为初级学习器,逻辑回归作为次级学习器进行集成。实验结果表明集成的异构分类器比同构分类器预测准确性更高。
1 材料与方法
1.1 实验材料
本研究采用MrOs Online(https://mrosdata.sfcccpmc.net/)上的美国男性骨质疏松性骨折研究数据,数据包含5 994 例男性病例样本,病例均为年龄在65岁以上的非卧床男子,其中有12.13%(727名)的患者主要部位(髋部、颈椎、腰椎、胸椎、腕部、肩部)发生过骨折。
选取MrOs 数据集中的骨相关数据作为基线数据,包括临床数据、骨密度数据、骨小梁评分数据、腹主动脉钙化数据以及病例骨折情况记录数据。每项基线数据均包含若干特征,如骨密度数据中包含髋部骨密度、股骨骨密度、腰椎骨密度等特征。对这些数据进行特征相关性分析,提取与骨折相关性较高的特征。部分基线数据描述如表1所示。
1.2 特征选择
特征选择是选择相关特征子集以用于模型构建的过程。本研究选用的相关数据文件中均包含众多特征,其中有许多冗余或不相关特征,它们会使得机器学习算法的训练速度降低,增加模型的复杂性,产生模型过拟合现象并会影响预测模型的准确性。因此对数据进行特征选择,考虑到所用学习算法较多,且对模型进行了集成学习,采用过滤式特征选择方法:通过数据的内在属性来估计特征的差异性,根据特征的差异性评分进行排序,并选取评分较高的一部分特征作为特征子集输入到分类算法上。过滤式方法计算简单快速,独立于分类算法,适用于不同的分类算法[8]。笔者选用过滤式中基于皮尔逊(Pearson)相关系数的算法。
Pearson 相关系数是衡量向量相似度的一种方法。输出范围为-1~+1,0 代表无相关性,负值为负相关,正值为正相关。其公式为:

其中,n为样本个数,Xi为选取的特征数据集,Yi为标签数据集,μX表示随机变量X的均值,μY表示随机变量Y的均值。从临床数据中提取身高、体质量、体重指数(BMI)等数据;骨密度数据中提取髋部骨密度、股骨骨密度、腰椎骨密度等数据;腹主动脉钙化数据中提取腹主动脉钙化评分数据;骨小梁评分数据中提取L1~L4腰椎段的骨小梁评分数据;并从骨折情况数据中提取病例主要部位骨折数据标签。经过相关性分析后,剔除与骨折数据标签Pearson 相关性低于0.6 的特征,对于存在高度相关的特征组(本研究取Pearson 相关性高于0.9)每组仅保留一个特征。最终筛选出骨小梁评分、腹主动脉钙化评分、身体质量指数、髋部骨密度、股骨骨密度、颈部骨密度T评分等共16个相关性较高的特征纳入模型中。
1.3 数据类别不平衡校正
本研究数据中只有12.13%的患者主要部位骨折,数据类别失衡较严重,若直接使用不平衡的数据进行实验,则多数类与少数类之间的不平衡将导致机器学习产生偏差,影响模型的性能。目前重采样技术是处理类不平衡问题的常用方法,例如过采样,欠采样和综合采样。其中过采样少数类虽可以平衡本文数据的类分布但无法解决数据集中存在的类重叠问题,并在使用分类器后易产生过拟合现象。本研究将过采样方法Smote 与数据清除方法Tomek links 相结合可以解决上述问题[9]。Smote+Tomek 方法不仅可以平衡数据,还能消除决策边界错误一侧的嘈杂示例,最适用于本研究这种具有少量正样本的数据集。
1.4 基于集成学习的骨质疏松性骨折预测模型
集成学习是一种使用多个基础学习器来提高预测准确性的机器学习技术。对分类器进行集成的思想是将一组分类器使用选定的结合策略通过多种方法(例如投票和平均)对新样本进行分类[10]。目前行之有效的集成技术是Bagging,Boosting,Stacking 和随机子空间(Random subspace)方法[11]。本文选用极端随机树(Extremely Randomized Trees,ET)、DTB 作为初级学习器,逻辑回归作为次级学习器,使用Stacking 算法对上述不同个体学习器进行集成,构建异构分类器以进一步提高模型预测精度。集成时初级学习器ET、DTB 的个数均取1,且ET、DTB 中决策树的集成度均为40。
Stacking 先从初始数据集训练出几个不同的初级学习器,并通过训练一个次级学习器来结合这些初级学习器[12]。用于训练次级学习器的数据集是一个新数据集。在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记[13]。我们需要定义初级学习器以及次级学习器来构建Stacking。本文Stacking 框架如下所述。
设基学习算法为Lk,Lk分别为ET、DTB。设基学习器为Ck:

其中,S表示本文骨质疏松患者训练数据集,且S中的样本为Si:

其中,Xi为筛选出的16 维特征向量,yi为主要部位是否发生过骨折。
使用交叉验证方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本。本文将数据集S分割为20份。此时设为数据集S中去除第j份数据子集后使用第k个基学习算法训练出的基学习器,其表示为:
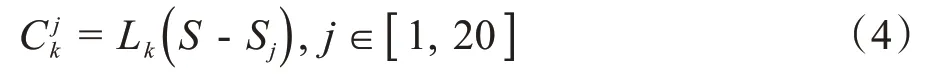
其中,Sj为第j份数据子集。将第j份数据子集中的特征向量作为基学习器的测试集来预测是否会发生骨折,预测结果表示为:

为每一份数据子集预测出患者发生骨折和不发生骨折的概率,得出基学习器的预测结果集为作为次级学习器的数据集,其中yj为该患者是否骨折的初始样本标记。
本文采用逻辑回归作为Stacking 的次级学习器算法,其模型可以表示为:

其中,xi∈xl,θ为需学习的参数,hθ(x)为逻辑回归的假设函数,其公式为:

将式(7)代入式(6)可得:

该模型的目标函数可以定义为:

其中,J(θ)为逻辑回归模型的代价函数,本文使用交叉熵作为代价函数,其公式为:
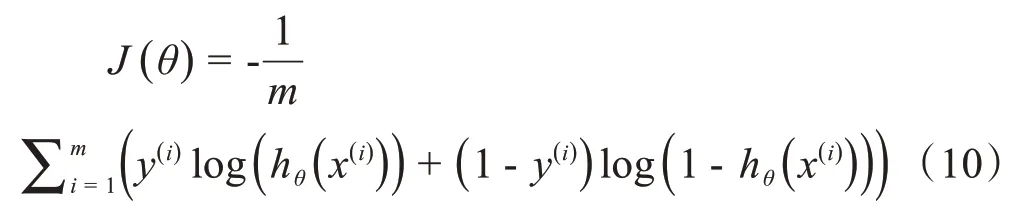
其中,m为训练样本的个数,y为样本的标签值。将基学习器学习所得的是否发生骨折的结果集xl作为逻辑回归模型训练样本的特征数据,将初始样本中病例是否骨折的标记yl作为逻辑回归模型的标签,最终训练得到本文基于Stacking的异构分类器EtDtb-S。
2 实验验证与结果分析
2.1 验证方法
为验证本研究的有效性,本文采用准确率(Accuracy)、精确率(Precision)、召回率(Recall)和F1值(F1)对各分类模型进行评估。

其中,TP为真阳性,表示实际骨折患者预测结果也为骨折;TN为真阴性,表示实际健康男性预测结果也为健康;FP 为假阳性,表示实际健康男性预测结果为骨折患者;FN为假阴性,表示实际骨折患者预测结果为健康。
本文将构建的EtDtb-S 模型与单模型以及同构分类器共8种模型进行对比,设标签为骨折的样本为正类样本,不骨折的样本为负类样本。用于实验对比的模型分为2 类:(1)单独使用ET 模型和DTB 模型;(2)使用不同集成学习方法(Bagging、Boosting、Stacking)分别对ET模型、DTB模型进行同构集成。
对比实验采用十折交叉验证,验证过程中每一折内类别标签比例随机,为减少因样本划分不同而引入的差别,本文重复进行10次十折交叉验证再取均值,得出以上共9 种模型的准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值(F1)以及相应标准差。
2.2 实验结果与分析讨论
本文数据集在不同模型下的分类预测结果及标准差如表2所示。
表2 9种模型预测结果及标准差比较(± s)Tab.2 Comparison of prediction results obtained by 9 models(Mean±SD)
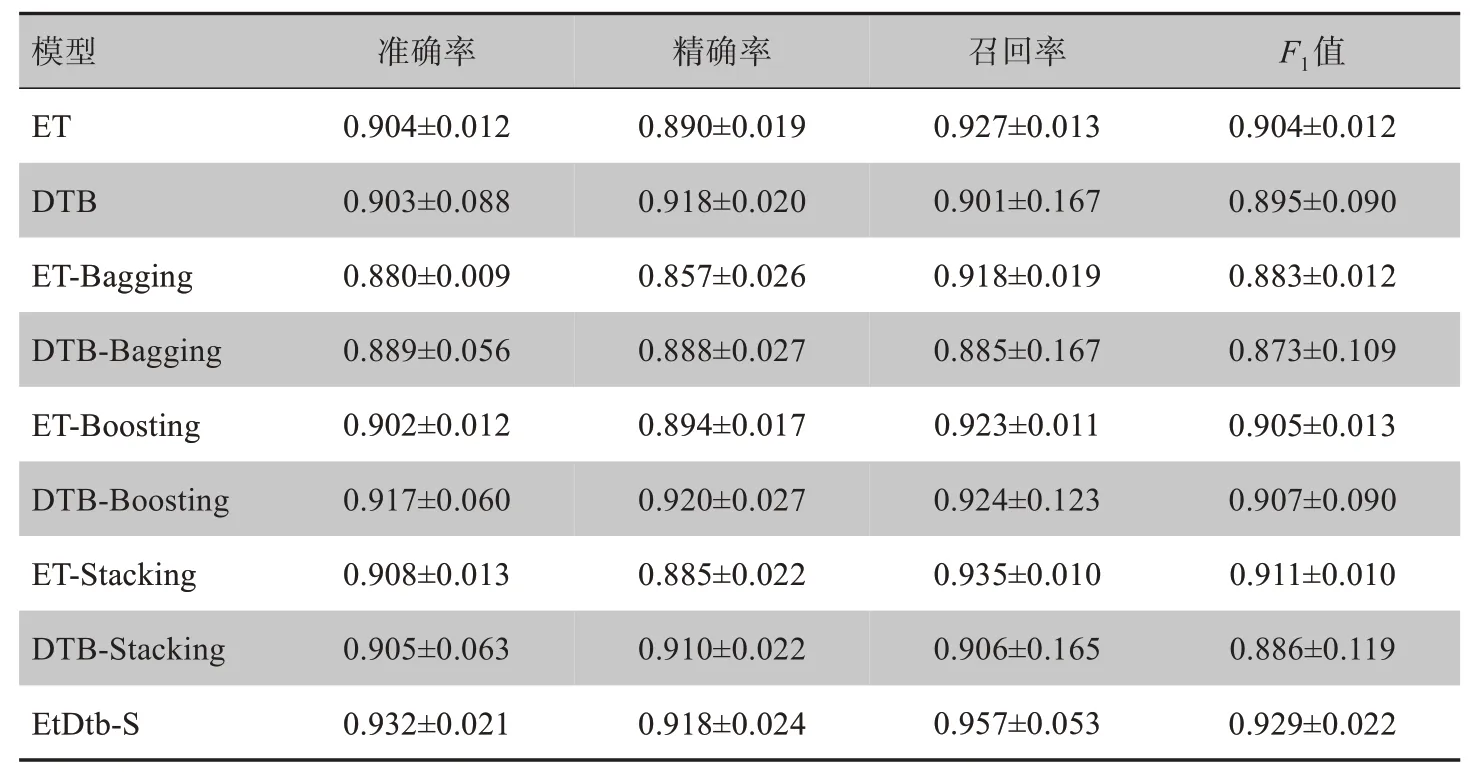
表2 9种模型预测结果及标准差比较(± s)Tab.2 Comparison of prediction results obtained by 9 models(Mean±SD)
模型ET DTB ET-Bagging DTB-Bagging ET-Boosting DTB-Boosting ET-Stacking DTB-Stacking EtDtb-S准确率0.904±0.012 0.903±0.088 0.880±0.009 0.889±0.056 0.902±0.012 0.917±0.060 0.908±0.013 0.905±0.063 0.932±0.021精确率0.890±0.019 0.918±0.020 0.857±0.026 0.888±0.027 0.894±0.017 0.920±0.027 0.885±0.022 0.910±0.022 0.918±0.024召回率0.927±0.013 0.901±0.167 0.918±0.019 0.885±0.167 0.923±0.011 0.924±0.123 0.935±0.010 0.906±0.165 0.957±0.053 F1值0.904±0.012 0.895±0.090 0.883±0.012 0.873±0.109 0.905±0.013 0.907±0.090 0.911±0.010 0.886±0.119 0.929±0.022
由表2 可以发现,本文异构分类器EtDtb-S 的分类精度为0.932,相较单独使用ET 的分类精度0.904和单独使用DTB的分类精度0.903,分别提高2.8%和2.9%。基于Bagging 对ET、DTB 分别进行集成的同构分类器ET-Bagging、DTB-Bagging 分类精度分别为0.880、0.889;基于Boosting 对ET、DTB 分别进行集成的同构分类器ET-Boosting、DTB-Boosting 分类精度分别为0.902、0.917;基于Stacking 对ET、DTB 分别进行集成的同构分类器ET-Stacking、DTB-Stacking 分类精度分别为0.908、0.905。本文的异构分类器相较上述同构分类器的分类精度提高1.5%~5.2%。由此可得出,本文异构分类器的分类精度优于单模型和同构分类器,分类效果最佳。
为比较上述分类器的性能,绘制出各分类器基于十折交叉验证的ROC 曲线,在得出每一折交叉验证的ROC 曲线下面积(AUC)值后求出AUC 的均值,结果如图1 所示。ROC 曲线越靠近左上角边界,即AUC 越大,表示分类器性能越好。由图1 可以看出,在ROC 曲线中,ET-Bagging 和DTB-Bagging 的AUC均值为0.95,DTB 和DTB-Stacking 的AUC 均值为0.96,ET、ET-Boosting、DTB-Boosting 和ET-Stacking的AUC 均值为0.97,本文异构分类器EtDtb-S 的AUC 均值为0.98。以上数据说明,本文提出的基于Stacking 的异构分类器EtDtb-S 相较于单模型和同构分类器分类性能最好。
3 总结与展望
本文介绍了一种用于骨质疏松性骨折预测的新的集成方法,使用Stacking 对ET、DTB 模型进一步集成构建出异构分类器EtDtb-S。首先,提出了基于机器学习理论的Stacking 集成方法的模型构建过程;其次,使用不同集成学习方法对本文集成方法中所采用的初级学习器分别进行集成,将单独使用初级学习器的模型、集成后的同构分类器与本研究的异构分类器分别对选取的特征变量进行训练;最后,通过十折交叉验证得出的准确率、精确率、召回率、ROC曲线比较各模型在测试集上预测的性能,验证本文提出方法的有效性。用Stacking 集成时初级学习器ET 和DTB 在模型结构和分类偏差上的差异性改善了集成后异构分类器的预测精度。实验结果表明,本文基于Stacking 的异构分类器能够正确预测骨质疏松性骨折的大部分病例,并且比单模型和集成的同构分类器预测准确性更高,具有最好的分类性能。
本文在运用Stacking进行模型融合的过程中将数据集分割成20份,叶子结点最少样本数为1,内部结点再划分所需最小样本数为2,决策树集成度为40,后续还将调整这些参数,以进一步提高模型性能。本研究还尝试过加入其它分类模型例如神经网络作为集成模型的基学习器,但最终预测准确率并不理想,后续将基于本文现有个体学习器的特征,尝试加入不同神经网络作为个体学习器,进一步提高模型的准确性和通用性。
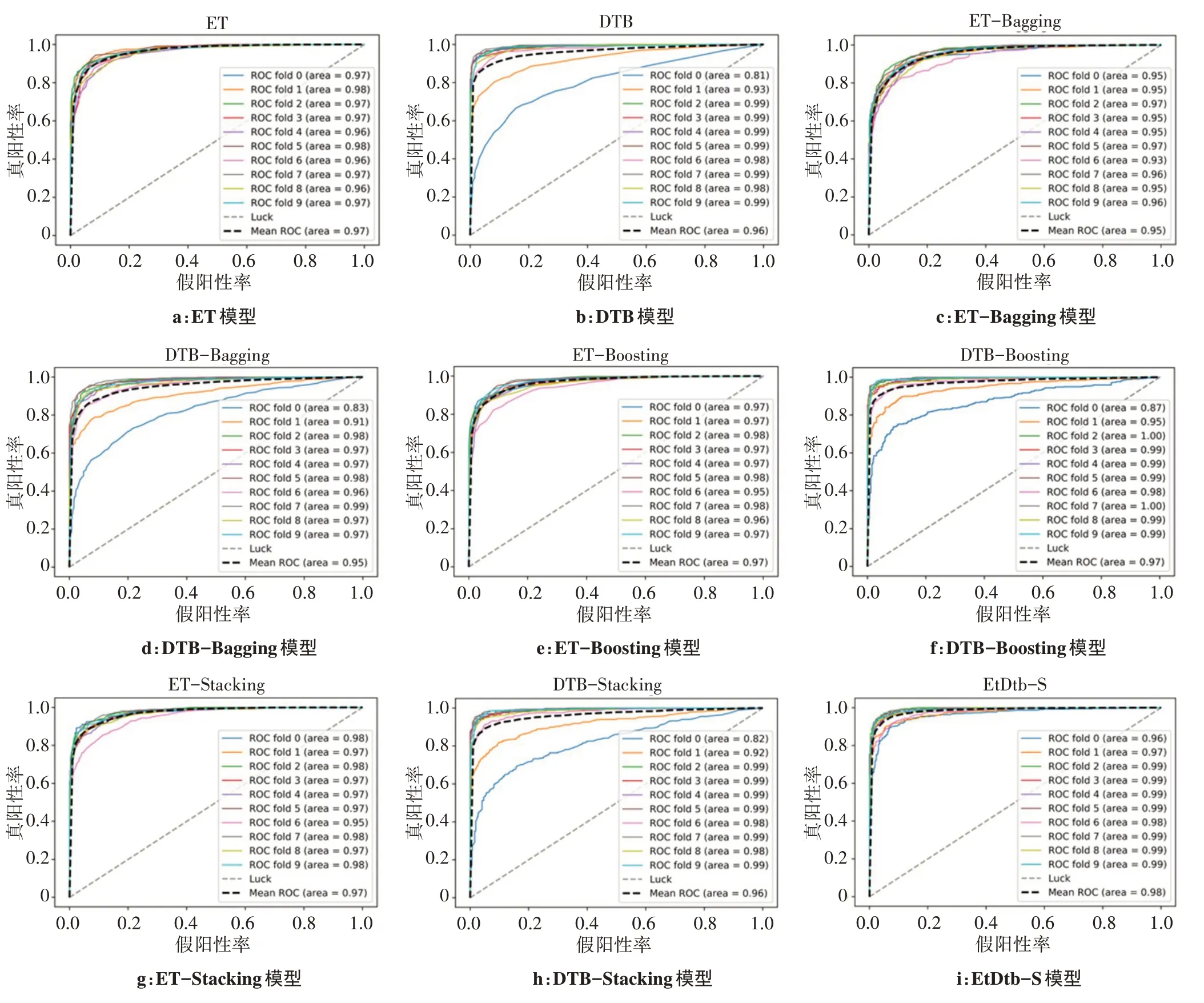
图1 9种模型ROC曲线对比图Fig.1 Comparison of receiver operating characteristic curves of 9 models
——以指数、对数函数同构问题为例

