基于蚁群优化算法的纠删码存储系统数据更新方案
李 乾 胡玉鹏 叶振宇 肖 叶 秦 拯
(湖南大学信息科学与工程学院 长沙 410082)(qianli160@hnu.edu.cn)
由于纠删码具备高可用性和高存储空间有效性的特点,采用纠删码为分布式存储系统以及数据中心[1-4]提供数据持久性已成为约定俗成的标准.纠删码把大数据对象划分成多个小的数据块,然后将这些小的数据块通过编码生成多个校验块,最后将这些数据块和校验块部署在不同存储群集的存储节点上.
数据更新在分布式存储系统中很常见[5-8].在许多企业的服务器和网络文件系统中,更新请求常常主导了写入工作负载(通常超过90%)[9-10].在典型的最大距离可分(maximum distance separable, MDS)MDS(n,k)纠删码存储系统中,1个数据块的更新请求涉及到n-k个校验块的更新.根据纠删码更新过程中是否有传输整个数据块,可以将更新分为2类:基于raid的更新和基于增量的更新.其中,基于raid的更新方案需要在数据节点和校验节点之间传输整个数据块,为了完成对数据节点的更新,数据节点首先需要收集所有新的数据块,然后重新计算更新后的校验块,并将其传到相应的校验节点.基于增量的更新方案只需要将数据节点上数据增量(数据块修改的部分)通过广播的方式传输到每一个校验节点,相比之下,基于增量的更新可以节省更多的IO操作和网络带宽.然而,频繁的数据更新也会导致巨大的IO操作和带宽开销.尤其在使用纠删码的键值存储系统中,对键值数据进行密集的小型更新会导致巨大的IO操作和昂贵的网络流量[7,11-15].
提高纠删码的更新效率具有十分重要的意义[16].最近一些研究工作者投入了大量精力来优化纠删码更新性能,以减少IO操作和降低网络时延[6,17-19].在现有的更新方案中,如CodFS[17]和Azure[20],采用追加式更新方式,或采用替换式更新和追加式更新的混合方式.一些研究者试图通过优化更新顺序和更新过程来减少网络传输开销[6,18-19].
从网络性能角度来看,数据增量最好是能够沿着数据节点与校验节点之间的最佳网络路径进行传输.虽然当前的路由算法能够可靠地处理分布式存储系统的大量网络流量[21-22],但是数据更新路由技术缺乏对异构存储系统(异构是指系统中的存储节点的吞吐量、IO速率不同,以及各段网络链路的有效带宽均不同)的深入研究,从而导致网络资源利用率不高.因此,优化大规模分布式存储系统路由极为重要,需要深入研究纠删码存储系统中数据更新路由.为了设计多目标路由优化更新算法,包括内存IO速率和其他服务质量(quality of service, QoS)指标,如时延和带宽,本文提出一种基于蚁群优化算法的多数据节点更新方案(ant colony optimization algorithm based multiple data nodes update scheme, ACOUS),ACOUS采用2阶段的数据更新过程来优化多数据节点的更新路由,并且使用基于多目标蚁群优化更新路由算法(multi-objective ant colony optimization update routing algorithm, MACOU)建立的更新树进行数据增量的收集和校验增量的分发.
具体而言,所提出的ACOUS方案采用集合式数据更新模式,主要包含2个阶段:在第1阶段,数据更新由数据节点触发.可以有多个数据节点(最多k个)进行更新,而其中的1个节点将被选为集合节点,其他所有数据节点计算数据增量并根据MACOU算法将数据增量发送到集合节点.在第2阶段,集合节点根据MACOU算法建立的多目标更新树,将较验增量依次分发到相应的校验节点.
本文的主要贡献有3个方面:
1) 针对大规模异构纠删码存储系统的内存吞吐量和跨节点链路带宽不相等的问题,本文提出的ACOUS是第一个深入研究异构纠删码存储系统中多数据节点更新过程和更新路由的工作.由于蚁群算法在解决QoS路由问题上的广泛应用[23],因此本文使用多目标蚁群优化算法来提高纠删码更新效率.
2) 分别定量分析了集合式更新和分布式更新方式下的数据更新IO操作数量和数据传输开销,分析了多个数据节点的更新路由问题.
3) 开发了一个原型系统,进行了大量实验以评估在典型数据中心网络拓扑下ACOUS的性能.实验结果表明,本文提出的MACOU更新算法优于TA-Update[5],在保证收敛性的前提下显著提高了更新效率.
1 背景及相关工作
本节先介绍纠删码以及蚁群优化路由算法的原理,然后介绍目前常用的纠删码的更新方法.
1.1 纠删码和蚁群优化路由算法
由于分布式存储系统有持久性和存储效率的需求,纠删码在大规模存储系统的应用成为研究焦点.众所周知,里德-所罗门码RS(n,k)[24](reed solomon codes, RS)纠删码首先将一个大小为D字节的文件分为k个大小相等的数据块di(1≤i≤k),每个数据块大小为Dk字节.然后,这些等大的数据块通过编码生成k个数据块和n-k个校验块,这些数据块和校验块组成一组(称为条带Stripe),分布在n个不同的存储节点(D1…Dk;P1…Pn-k)中,这n个节点属于不同的群集,以此来最大限度地提高系统的可靠性.每个校验块pj(1≤j≤n-k)根据式(1)进行计算,其中表示di到pj的系数.基于这种线性编码,n个块中任何不多于k个块出现故障就可以重建整个原始文件.
(1)

(2)
蚁群算法是一种启发式智能优化算法,可以用来在图中寻找最优路径,该算法起源于在环境变化后,蚂蚁通过感知其他蚂蚁留下的信息素这种相互合作方式快速找到到达食物源的最短路径.蚁群算法已经被用来解决一系列组合优化问题,如最短路径问题、最优任务分配问题、QoS路由问题等[23].其原理是每只蚂蚁在爬行的过程中都会留下信息素,每条路径上的信息素随着时间的推移不断增加或减少,所有的蚂蚁在爬行时更倾向于选择信息素更多的路径.定义时刻t+1节点i到节点j的路径上的信息素的数量为
τij(t+1)=(1-ρ)τij(t)+Δτij(t),
(3)
(4)
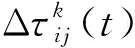
每只蚂蚁在爬行的过程中,当下一时刻有多条路径可以选择时,蚂蚁选择某条路径的概率又会受到可选路径上信息素的量和全局启发式因子的影响,式(5)说明了蚂蚁从节点i移动到节点j的公式,这个公式也称为状态转移公式.
(5)
其中,φk(i)表示节点i的下一跳候选集,ηij是蚂蚁从节点i移动到节点j的全局启发式因子,α和β分别表示信息素和全局启发式因子的权重.通过这种方式,每条路径上的信息素的数量不断地增加或者减少.最终所有的蚂蚁都会沿着最短的那条路径爬行,这也称为蚁群算法的收敛性和正反馈机制.
1.2 相关工作
目前存在2种删除纠删码的更新方案,分别是基于raid的更新和基于delta的更新.基于raid的更新方案需要在数据节点和校验节点之间传输整个数据块.基于delta的更新只需要在数据节点和校验节点之间传输原数据块和新数据块之间不同的部分.与基于raid的更新方案相比,基于delta的更新方案数据传输量更小,后者数据更新效率更高.因此,本文采用基于delta的更新方案.在基于delta的更新方案中,又存在3种更新方式,分别为覆盖式更新、追加式更新和混合式更新.
覆盖式更新方式通过利用新数据直接覆盖原始数据块和校验块,实现了数据的实时更新.因为覆盖式更新能够确保数据的一致性和恢复效率,所以它被广泛地应用于纠删码的更新.但是为了完成检验块的更新,覆盖式更新方式又引入了大量的IO操作和网络开销[5].
混合式更新方式是在允许数据块和校验块异步更新的前提下,数据块采用覆盖式更新,校验块采用追加式更新.这种更新方式可以确保数据块的访问效率以及校验块的更新效率.比如PL[26],PLR[17]采用覆盖式更新方式,直接用新的数据覆盖原始数据块,然后将校验增量追加在校验块之后.
总而言之,以上3种更新方式中,数据节点必须向校验节点发送数据增量,以保证数据一致性.而ACOUS与现有的方法不同,不是关注单个节点的数据更新操作,而是优化整个更新过程中的IO开销,并且致力于提高数据传输效率,针对多个QoS指标提高纠删码更新效率.
多约束QoS路由问题是一个典型NP-C问题[23].由于蚁群算法具备鲁棒性和收敛性,已成功地应用于求解许多离散优化问题.蚁群优化技术在解决QoS路由问题中得到广泛的应用.文献[27]采用基于蚁群优化的路由技术,将节点的实时位置和负载2个参数作为路由指标,以提高网络的QoS性能.文献[28]提出了一种改进的基于蚁群算法的动态源路由方案,该方案可以在较低的时延、较低的路由开销以及较低的能耗的情况下产生高数据包投递率.文献[29]利用蚁群算法提高以信息为中心的网络性能.
2 挑 战
通常情况,在大规模分布式存储系统中执行碎片化的、小数据块的纠删码更新操作可能导致性能显著下降.这是因为数据更新涉及到多个校验节点的更新,这不可避免地会导致相当大的IO和带宽开销.尤其是对于分布式存储系统的更新操作,例如,云存储系统、分布式内存键值存储系统和块存储系统,大多数都是写请求,这将导致较大的时延.云存储系统Azure[20]采用了基于日志的更新方案来分摊更新开销.分布式键值存储系统中的更新操作可能会导致一些小的更新,这将引入巨大的编码操作和网络流量.例如,在基于Memcached的Cocytus[11]中,对于密集的小规模更新操作,即set操作,需要频繁地修改分布在多个校验节点上的数据.对于纠删码的磁盘阵列或块存储系统文件,如结构化数据库文件和虚拟机文件系统,对一个文件的更新可能导致多个节点在不同的集群中同时需要进行更新操作[8].纠删码更新主要面临如下挑战:
1) 当有多个数据节点需要更新时,这些节点之间的协作会导致大量的有限域运算和网络流量.根据式(2),虽然增量和编码计算可以并行地在所有数据节点上高效执行以完成更新,但如何协调更新的数据节点,以最小的网络流量将增量发送到相应的节点仍是一个难题.
3 多个节点更新的路由问题分析
3.1 纠删码存储系统多数据更新的2种模式
当有多个数据节点需要更新时,有2种更新模式:分布式和集合式.图1(a)显示了分布式更新模式的更新过程,其中用于更新的每个数据节点分别向每个校验节点发送Δdi.图1(b)显示了集合式更新模式的更新过程,所有更新的数据节点Di在完成更新之后计算Δdi,并将其发送到集合节点(rende-zvous node, RN),由集合节点计算Δpj,然后将Δpj发送到相应的校验节点Pj.
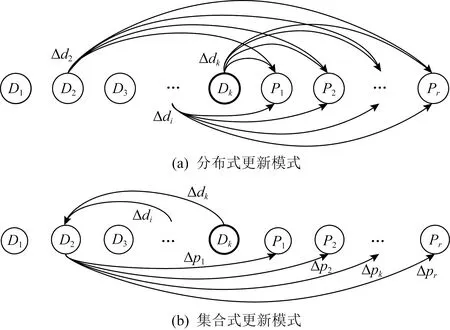
Fig. 1 Two update patterns for multiple data nodes图1 多数据节点更新的2种模式
表1显示如果u(1≤u≤k)个数据块需要更新,2种更新模式产生的数据传输开销和数据读写开销.从表1可以看出,2种模式在并行计算下的IO开销几乎相同.分布式更新模式下的数据传输开销随着u的增加迅速超过了集合模式中的数据传输开销,因此本文采用集合式更新模式来完成多节点更新问题.

Table 1 The Overhead of Two Update Patterns When u Data Nodes for Update
3.2 路由的QoS度量
本文的目标是围绕3个典型的QoS指标进行研究,以提高大规模异构纠删码存储系统中多个数据节点的更新效率.
1) 距离.节点s到节点d之间的距离D(s,d)是根据2个节点之间的跳数计算,距离通常被用来构建数据传输的最小生成树,由于网络的物理拓扑结构在一段的时间内保持稳定,TA-Update[5]基于Prim算法以网络距离作为度量来构造更新树,通过更新树可以反映节点之间的路径长度,同时更新树的构造是以数据节点为根节点,采取自上而下的数据传输方式,最终的目的是使得整个更新过程数据传输距离最小.网络距离越小表示数据传输的跳数较少,意味着数据传输时延较小.
2) 带宽.带宽是衡量网络中链路容量的指标.数据传输的瓶颈由传输路径上的最小带宽确定[30],由于存储节点之间链路上带宽是异构的,树状的拓扑结构由此形成,文献[30]利用带宽来构造再生树,并将再生树的构建和再生码进行结合,从而有效利用存储节点之间每条链路上的可用带宽,降低网络流量,提高再生码的恢复效率.但实时可用带宽难以获得,因此,本文利用平均带宽B(e)作为链路e的带宽,B(s,d)表示路径p(s,d)上的最小平均带宽.
B(s,d)=min{B(e),e∈path(s,d)}.
(6)
3) 时延.本文采用时延作为衡量更新效率的关键指标.时延越小代表数据传输效率越高.路径path(s,d)上的总时延delay(s,d)是处理时延dproc、传输时延dtrans和传播时延dprop之和.式(7)表示总时延的计算方式,本文没有考虑计算排队时延,因为排队时延超出了本文的讨论范围.
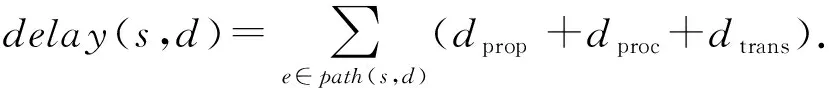
(7)
距离、带宽、时延这3个因素是影响纠删码更新的主要网络因素[5],但是TA-Update仅以距离为度量并基于Prim算法来构造更新树,存在局限性.本文利用多目标蚁群优化算法可以综合考虑这3个因素,实现多目标优化,以此提高纠删码的更新效率.
4 基于蚁群优化的多数据节点更新方案
本节将针对3.2节列出的3个QoS指标详细说明ACOUS更新方案.首先介绍2阶段集合式更新模式的过程,然后介绍多目标蚁群优化更新路由算法.
4.1 集合式更新的2个阶段

Fig. 2 The two-stage rendezvous update scheme图2 集合式更新的2个阶段
ACOUS的主要思想是采用2阶段集合式更新方案,多目标更新树实现对RS(k+r,k)编码高效的数据增量收集和校验增量分发.

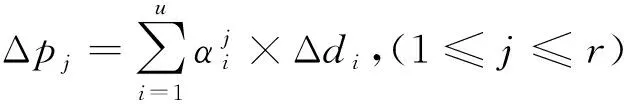
4.2 多目标蚁群优化更新路由算法
表2解释了算法中涉及的符号.式(8)描述了节点s和节点d之间的最佳更新路径的问题.其中节点的权重代表节点的处理时延以及传输时延的大小,边的权重代表传播时延的大小.
arg min{delay(s,d)}, s.t.B(e)≥Breq,
e∈path(s,d).
(8)

Table 2 Ant Colony Algorithm Parammeters表2 蚁群算法参数
算法1详细描述了MACOU算法,其目的是在带宽约束下搜索从节点s到节点d的最小时延的路径.
算法1.多目标蚁群优化更新路由算法MACOU.
输入:网络拓扑图G(V,E)、每个节点的权重Wi(i∈V)和每个边的权重We(e∈E)、每条边的带宽B(i,j)和最小带宽Breq约束、源节点s和目标节点d;
输出:满足最小带宽约束下时延最小的路径p(s,d).
① 初始化α,β,λ,k,m,i=s,converge=false;
② 初始化每条路径上的信息素τ;
③ 计算每个节点i到目的节点d的距离D(i,d),i∈V;
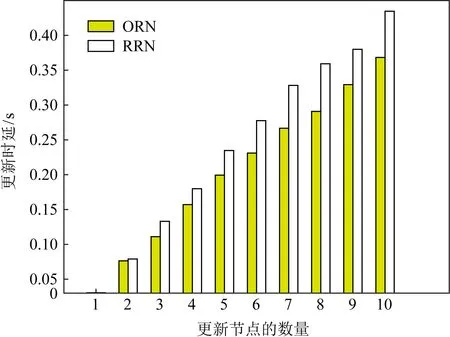
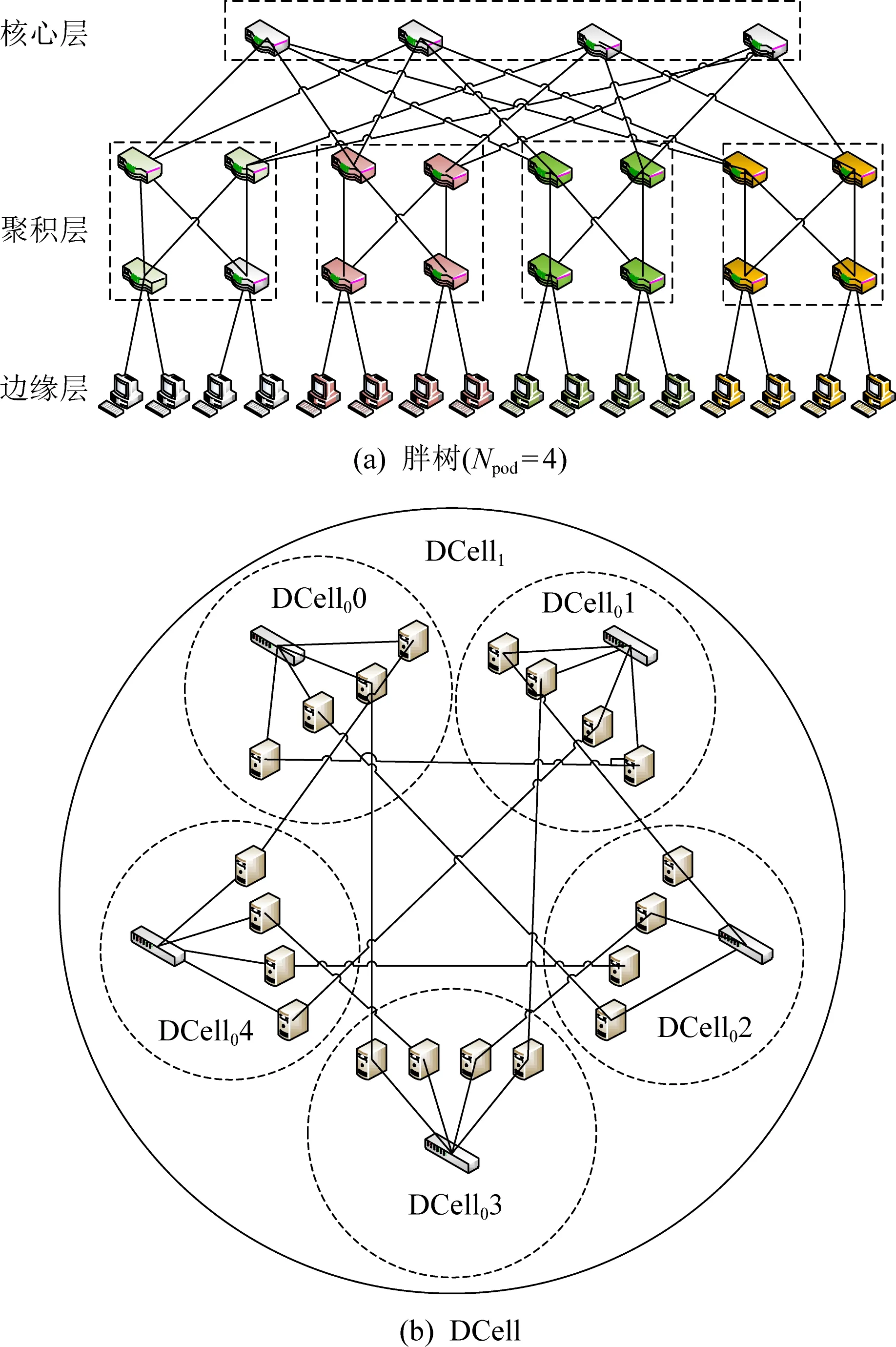
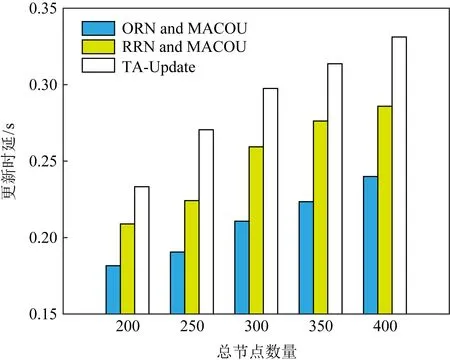
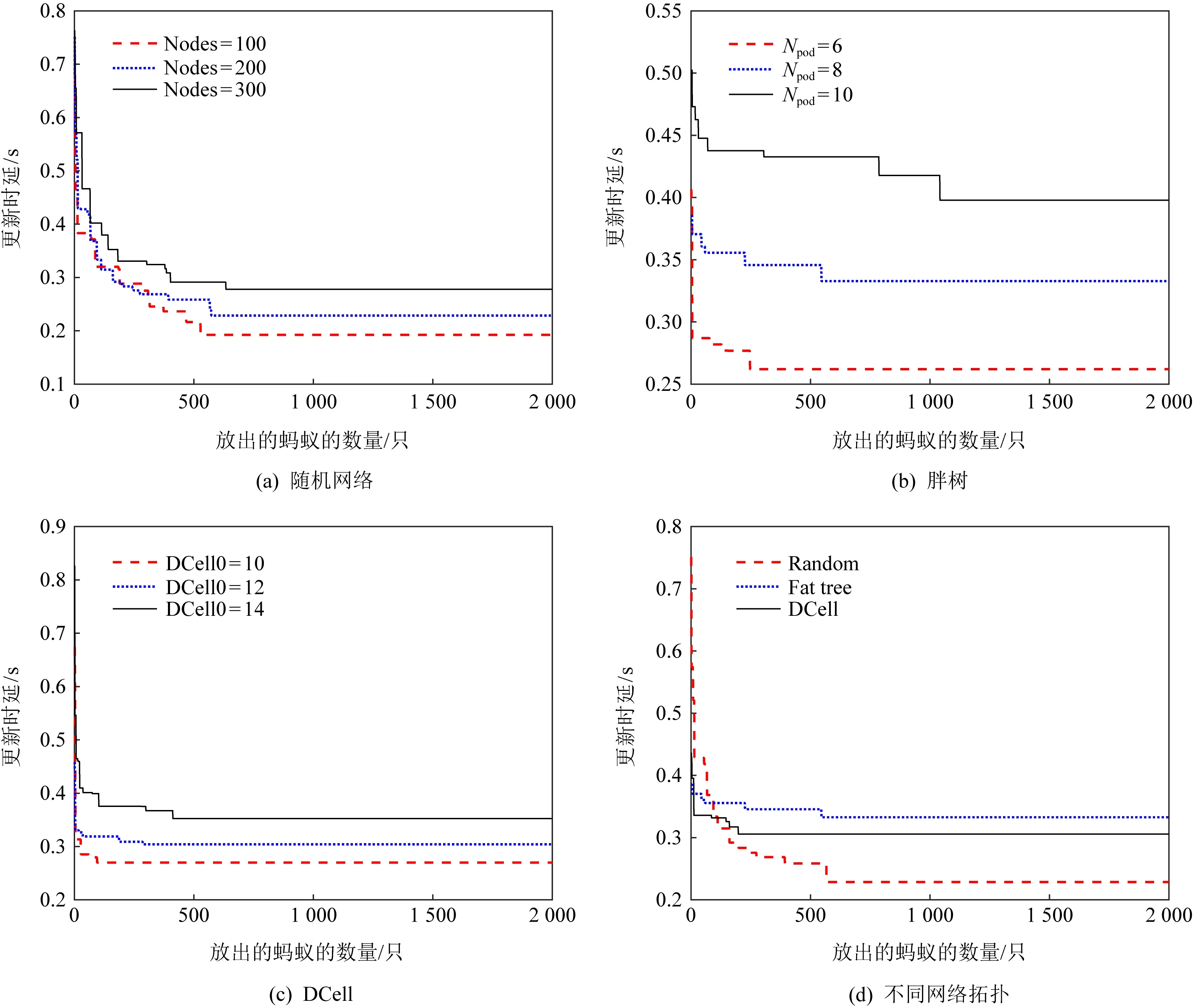
④ for (m=0,m ⑤ for (k=0,k ⑥ whilei≠d或φ(i)≠∅ do ⑦ for eachj,j∈φ(i) do ⑧ 计算概率Pij; ⑨ end for ⑩ 从Pij中选择最大的Piv,v∈φ(i); MACOU算法首先根据输入初始化行①②中每个参数的值,行③计算每个节点到目标节点的距离. η(i,j)=(1(D(j,d))β×(1(Wi+We))λ, (9) 例1.图3说明了MACOU算法的过程.图3(a)是多目标更新树,其中V1是集合节点,其他所有节点为校验节点.在图3(a)中节点权重代表时延的总和,边的权重代表带宽的大小.在实际的分布式存储系统中,所有节点都通过树状拓扑结构连接,其中一些节点连接底层交换机,然后底层交换机连接上层交换机.节点之间的所有路径都通过交换机中继.每条边的权值表示其可用平均带宽(单位是Mbps).每条边的权值表示其可用平均带宽.假设最小带宽要求是Breq=50 Mbps,本文需要找到一个具有最小时延的更新树,其每条边e应满足B(e)≥50 Mbps.本文提出的更新路由算法MACOU可以在网络初始化过程中进行部署,因此,每个数据节点能够在一段时间内保持到每个校验节点的最优路由,直到下一次网络重新配置.图3(a)中的黑色粗线箭头和所有节点的边构造了以V1为根节点的多目标更新树. 图3(b)描绘了路径p(V1,V7)的搜索步骤.蚂蚁从V1开始,在初始信息素相同的情况下,由于B(V1,V2) <50 Mbps,因此下一跳是V3.类似地,蚂蚁从V3出发,距离D(V2,V7)=2,距离D(V4,V7)=D(V5,V7)=1.但是,V5的时延大于V4.所以,蚂蚁选择V4作为下一跳.最后,V4可以直接到达V7.由于MACOU的正反馈机制,选择路径:V1→V3→V4→V7的蚂蚁数量越多,该路径上的信息素就越多.因此,经过多次迭代后,从V1到V7的路径最终收敛于V1→V3→V4→V7,且这条路径满足最小更新时延和带宽约束. Fig. 3 A case study of multi-objective update tree construct with MACOU图3 基于MACOU算法的多目标更新树 类似地,本文可以找到V1到其他校验节点最佳更新路径,并由此构造出类似图3(a)中的更新树.值得注意的是,第1阶段的数据增量收集也可以利用MACOU算法和校验增量分发的方式构建.MACOU与图3(a)中基于Prim算法的TA-Update方案形成的虚线箭头组成的更新树相比,前者具备更小的更新时延.例如,需要搜索从V1到V2的路径,由于带宽约束,通过MACOU算法搜索出的路径是V1→V3→V2,比TA-Update搜索的路径V1→V2效率更高.2条路径之间的总时延随传输数据包大小的增大而增大,例如,传输大小为1~9 MB的数据包,路径V1→V3→V2和路径V1→V2的时延分别是0.03~0.27 ms和0.033~0.3 ms. (10) 算法2.ORN选择过程. 输入:网络拓扑G(V,E)、每个节点的权重Wi(i∈V)和每条边的权重We(e∈E)、每条边上的带宽B(i,j)、需要更新的数据节点的集合D和校验节点的集合P; 输出:DORN. ① 初始化sumdelay[i]=0; ② for eachDiinD′ do ③ for eachDk(Dk≠Di) inD′ do ④ 使用算法1计算时延delay(Di,Dk); ⑤sumdelay[i]=sumdelay[i]+ delay(Di,Dk); ⑥ end for ⑦ for eachPjinPdo ⑧ 使用算法1计算时延delay(Di,Pj); ⑨sumdelay[i]=sumdelay[i]+ delay(Di,Pj); ⑩ end for 本文通过在原型系统上进行实验,以验证ORN和RRN的更新效率.如图4所示,随着更新节点数量的增加,在忽略集合节点选择计算的情况下,ORN的时延比RRN的时延更低.在存在30多个节点原型存储系统中,基于MACOU算法获得的路由信息,算法2的选择过程不超过0.01 s.值得注意的是,在网络重新配置之前,MACOU算法为每个数据节点获取的路由信息在一段时间内不会频繁更新.因此,考虑到计算资源的普遍可用性,大规模存储系统最好选择ORN.由于计算成本可以忽略,本文在第6节中对2个不同的集合节点的更新时延进行了更多的评估,由于节点的更新序列是随机的,ORN基本均匀分布在不同的节点上,可以实现负载均衡,因此ORN节点的性能不会成为纠删码更新效率的瓶颈. Fig. 4 Comparisons of update delay under different RNs图4 不同RN下的时延 本文在基于存储集群的腾讯云虚拟机上实现了ACOUS更新方案,并研发了一个原型系统(1)https://github.com/599020328/acous来评估本文提出的方案.同时本文在更大的网络拓扑(大于200个节点)上进行仿真,以进一步评估本文的更新方案.属于同一条带的数据节点和校验节点通常被随机部署在不同的集群中.由于ORN中集合节点选择操作的时延通常是以微秒为单位,与数据更新时延相比可以忽略,因此本文在下面的评估中忽略了计算时间. 本文的原型存储集群由多达35台腾讯云虚拟机(Ubuntu服务器14.04.1 LTS,4 GB RAM和双核Intel Xeon Cascade Lake (2.5 GHz))组成,它们通过带宽为1.5 Gbps的网络连接在同1个子网中.本文利用腾讯云的性能监测工具来估计平均带宽. 在图5中,我们提供了不同方案下更新时延的广泛比较.如图5(a)所示,当r=3时更新时延随更新数据节点数量k增加的情况.如图5(b)所示,当k=5时,更新时延随校验节点数量r增加的情况.随着数据节点或校验节点数量的增加,将会有更多的数据增量和校验增量沿着本文方案中最优更新树有效地传递.因此,当k或r增加时,本文的方案能够减少更多的更新时延.与TA-Update相比,MACOU方案降低了30%~32%的更新时延. 如图5(c)所示,本文的原型系统在有5个数据节点和5个校验节点需要更新的情况下,系统中不同节点数量下的更新时延,这些节点随机部署在不同的存储集群中. 随着节点数量的增加,本文将它们安排到更多的存储集群中以实现负载平衡,从而产生了更多的传递跃点和数据包中继.因此,随着存储系统的扩展,本文的方案与ORN和MACOU结合后降低的时延从28%迅速增加到37%左右.如图5(d)所示,随着数据增量增加,本文的方案可以减少的时延几乎线性增加的. Fig. 5 Experiment in prototype system图5 原型系统中的实验 本文在基于组件的模拟器OPNET[31]上进行了大量的实验,以评估本文在大规模异构分布式存储网络系统中更新方案的性能,并且该系统定期执行更新.除了构建IO和带宽的随机拓扑结构外,本文还评估了其他2种典型数据中心网络拓扑的更新方案,如图6所示,即Fat tree和DCell,这2种网络拓扑结构都有很高的网络容量和健壮的连通性.在相同的条件下,本文还在相同的条件下与TA-Update方案进行对比.表3列举了仿真系统的一些关键参数. 6.2.1 不同大小数据传输量的系统更新时延 本节比较了不同数据传输量下更新时延的仿真结果.首先比较了在传输不同数据增量时,ORN和MACOU、RRN和MACOU与TA-Update方案更新效率的不同,如图7所示,更新时延随着传输数据增量的增大而增大.可以看到,与TA-Update方案相比,采用RRN和MACOU的方案可以节省大约26%的更新时延,采用ORN和MACOU方案的时延降低了18%左右. Fig. 6 Two typical data center network topologies图6 2种典型的数据中心网络拓扑 Table 3 Experiment Parameters表3 实验参数 Fig. 7 Delay under data delta图7 数据增量下的时延 图8显示了当k=9时,更新时延随r增加的情况.图9显示了当r=5时更新时延随k增加的情况. 与图5中原型系统的评估结果一致,随着数据节点或校验节点数量的增加,本文方案的优势变得更加明显.可以看到,本文采用ORN和MACOU的方案与TA-Update相比,时延降低了30%. Fig. 8 Delay under varying r when k=9图8 更新时延随r的变化 Fig. 9 Delay under varying k when r=5图9 更新时延随k的变化 6.2.2 不同规模的系统更新时延 图10描述了当更新的数据节点和校验节点的数量分别占总节点数量的5%时,不同大小规模下的更新时延情况.这些用于更新的节点随机部署在定期启动更新过程的存储系统中.随着系统规模的增大,TA-Update更新方案与本文采用ORN和MACOU的方案相比,TA-Update更新的时延增加得更快.图11显示了系统中只有5个数据节点和5个校验节点进行更新时,系统中总节点数在不同情况下的时延.根据图5(c)原型系统的评价结果,并从图10和图11可以看出,由于本文采用了ORN和MACOU结合的方案,随着系统的扩展,纠删码的更新效率明显优于TA-Update算法.因此,当节点数超过250时,本文的方案可以将更新时延降低28%~30%. Fig. 10 Update delay under the varying system scale图10 不同网络规模下的时延(r,k占总节点5%) Fig. 11 Update delay under the varying system scale图11 不同网络规模下的时延(r=5,k=5) 6.2.3 不同网络拓扑的更新时延 为了进一步研究本文提出的方案的适应性,如图6所示,本文在2个典型的数据中心网络拓扑结构(即胖树和DCell)下进行了大量的实验.Fat tree拓扑网络分为3个层次:自上而下分别边缘层、汇聚层和核心层,其中汇聚层交换机与边缘层交换机构成一个pod.在图12和图13中给出了在不同数据中心拓扑结构下更新时延的实验结果.与之前的实验结果类似,本文的方案也能够节省几乎相同的时延,这表明本文提出的方案具有良好的适应性. Fig. 12 Update delay under varying scale of Fat tree图12 不同规模的胖树结构下的时延 Fig. 13 Update delay under varying scale of DCell图13 不同规模的DCell结构下的时延 如图13所示,当本文设置MACOU算法的相关参数α=1,β=1,λ=1.6,ρ=0.4时,更新时延随着蚂蚁数量的增加而迅速减少,然后达到最佳蚂蚁数量的下限,最后实现搜索路径的收敛.信息素的定期更新使蚁群算法能够快速收敛,图14评估了本文的方案的收敛性.当图14(a)中的总节点个数为300时,在释放的蚂蚁数约为500个时实现了路径的收敛.如图14(a)~(c)所示,在较大的网络规模中通常会导致较慢的收敛.例如,图14(b)中当pod的数量Npod分别为6和8时,最佳蚂蚁数量接近250和500,而当pod数量Npod=10时,需要大约1 000个蚂蚁才能完成更新路径搜索.在图14(d)中比较了由200个节点组成的3种网络拓扑下的更新方案的收敛速度.可以看到,在DCell拓扑结构中,由于其高效的全局连接性,本文的方案在蚂蚁数量达到230左右时实现了最快的收敛速度.相反,由于随机网络的复杂性和冗余性,随机网络拓扑收敛速度最慢. Fig. 14 Update delay with increasing number of ants 图14 随着蚂蚁数量增加的更新时延 针对分布式纠删码存储系统中的频繁数据更新问题,本文尝试考虑多个QoS度量下的多数据节点的数据更新优化问题.本文提出的ACOUS更新方案是基于MACOU算法,采用2个阶段来优化多个数据节点更新.具体来讲,在数据更新过程中,使用基于蚁群优化路由算法构建的多目标更新树来实现数据增量的收集和校验增量的分发.在典型的数据中心网络拓扑下,与TA-Update更新方案相比,大量实验结果表明,本文的ACOUS更新方案以忽略不计的计算开销为代价实现了MACOU算法收敛,从而将纠删码的更新时延降低26%~30%. 贡献声明:李乾负责论文的所有实验和论文撰写,胡玉鹏对论文研究方案做全面指点和论文修改,叶振宇参与论文实验模拟验证,肖叶参与论文后期修改,秦拯参与论文后期修改.
j∈φ(i).
5 集合节点的选择
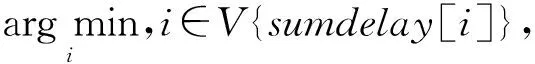
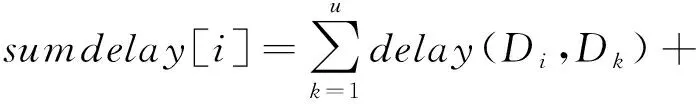
6 实验评估
6.1 原型系统评估

6.2 大规模网络仿真







6.3 收敛性分析
7 结 论

