一阶动态电路暂态过程分析及其仿真测试
付 扬,宋 磊
(1.北京工商大学 计算机与信息工程学院,北京100048;2.安标国家矿用产品安全标志中心,北京100013)
0 引 言
含有动态元件电容或电感的一阶电路,换路后一般要经历暂态过程才能达到新的稳态。在实际工程中,认识和掌握暂态过程这一物理现象的规律具有很重要的意义。
传统实验室研究一阶电路用双踪示波器观测,存在以下弊端:其一是不能同时观测电阻和电容输出波形,因为需要将观测的元件与电源共地,所以需要重新改接电路分别观测,同时元件参数变化时,也要重新改变电路,使得操作繁琐;其二是不能将不同输出、不同元件参数的波形集于一体观测,使得对一阶电路暂态过程规律显示不够全面直观和清晰;其三是对于正弦激励,示波器观测不到暂态过程,使得对产生的过电压缺乏认识,从而不能防范其危害[1]。
Multisim仿真是对电子电路设计、电路功能测试的现代实验手段,其提供了功能全面、高效、一体化的设计环境,方便完成电路设计、多种电路仿真分析和功能测试,如同真实实验环境一样;而分析功能之全是真实实验环境所不及的,可以非常方便有效地完成对电路的设计和仿真分析[2]。
将Multisim用于一阶RC电路暂态过程中,解决了实验室研究的弊端。利用Multisim参数扫描分析的功能,自定义观测所有元件的输入/输出波形,并同时可以根据R,C参数变化分析对输出的影响;利用其瞬时分析仿真功能,实现了正弦激励下暂态过程的测试,使得实际应用中合理选择参数,规避过电压的发生,同样可以分析RL电路过电流的发生,以实现动态电路设计和应用的高可靠性[3]。
1 一阶RC电路理论分析
1.1 一阶RC电路的求解
一 阶RC电路如 图1所示,t=0时开关K闭合,根 据KVL和电容的特性方程,可得到换路后的RC电路的一阶微分方程:
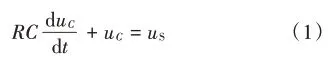
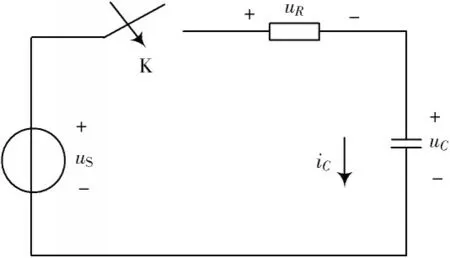
图1 一阶RC电路
该微分方程的解在t≥0时,由特解RTT和齐次微分方程的通解组成u′C(t),通解又称暂态解,即其解为uC(t)=u′C(t)+u″C(t)=uC′(t)+Ae-tτ,通解中的积分常数A可由初始条件确定,若uC(0+)表示电容电压换路后的初始值,u′C(0+)表示特解的初始值,时间常数为τ=RC,得A=uC(0+)-u′C(0+),因此有微分方程(1)的解为:
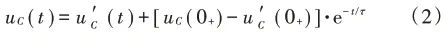
若电源为恒定激励,稳态解为u′C(t)=u′C(0+)=uC(∞)是一常数,由式(2)得:
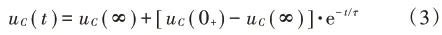
即需要知道三个要素:初始值uC(0+)、稳态值uC(∞)、时间常数τ=RC。
若正弦激励,稳态解为正弦稳态分量,u′C(t)=uC(∞),由式(2)得:

则需在前面三个要素的基础上,增加一个要素:稳态解[4]的初始值u′C(0+)。
1.2 方波激励下的响应分析
脉冲信号和正弦信号是动态电路常用的激励。观测脉冲信号作用下的响应时,微分电路和积分电路是两种典型电路。
1.2.1 微分电路
图1 中方波信号源周期为T,当t≪T2时,暂态过程快,此时电容器充放电快,电压很快达到稳态值uS,即uC≈uS,则即电阻输出电压与激励的微分成正比,此时电阻电压出现尖峰脉冲信号,电容很快充放电结束。
1.2.2 积分电路
当t≫T2时,暂态过程缓慢,电容器充放电慢,即uR≈uS,则,即电容输出电压与激励的积分成正比,电容输出电压为三角波,t越小,上升或下降斜率越大[5]。
1.3 正弦激励下的响应分析
设uS=Usinsin(ωt+φS),正弦电路接通后,一般要经过4τ~5τ的时间后,暂态解基本消失,电路可进入正弦稳态,进入正弦稳态后,电路所有电压、电流均受正弦交流电源的控制,均为与电源同频率正弦波,故稳态解可用相量法求解[6]。
电容电压相量为:
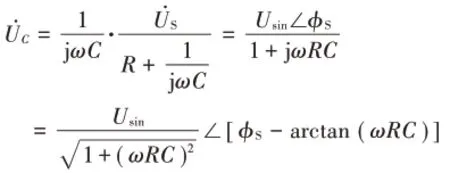
由上式得电容电压正弦稳态的幅值和初相:

所以正弦激励的正弦稳态分量为u′C(t)=UCmsin(ωt+φC),代入方程(4)得t≥0时,微分方程(1)的解为:
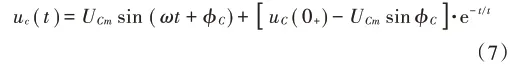
从式(7)可以看出,暂态解与电压初始值、信号源初相以及电路参数RC有关,t越大,相同时间暂态解的值越大。当电路参数一定,在一定条件下将出现过电压情况的暂态过程。下面根据电容的初始值不同,分析式(7)暂态过程的过电压:
1)若u(0+)=0 V,φC=±90°,此时由式(6)得电源初相如式(8):
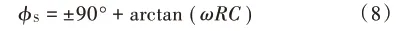
由式(7)得电路的响应:
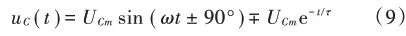
由式(9)可见暂态过程将出现过电压现象,过电压将发生在接近半周期处,其值还与电路的时间常数有关[7]。
2)若u(0+)=UCm,φC=-90°,则由式(6)得φS=-90°+arctan(ωRC),由式(7)t≥0得:
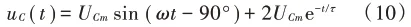
可见同样在接近半周期处,将出现过电压。
2 方波激励下的暂态过程仿真测试
在Multisim下构建图1电路,取方波激励峰-峰值为UP-P=-3~3 V,频率f=1 kHz,周期为T=1ms。分别选择t≪T2和t≫T2分析电阻和电容输出仿真波形,研究暂态过程。
2.1 微分电路仿真测试
取t≪T2,在方波的正值、负值期间,都相当于是在直流恒定电源作用下的一阶电路,由于时间常数小,电容器充电过程相当于在恒定电源3 V作用下,由-3 V充电到3 V;电容器放电过程相当于在恒定电源-3 V作用下,由3 V放电到-3 V。充电暂态过程可由三要素式(3)计算充电时间为τ时的电容电压,计算得uC(τ)=0.792 V,据此可由仿真确定时间常数τ。
选择Multisim下参数扫描分析仿真(Parameter Sweep),并设定相应选项,结束时间选2 ms,分析时电容参数固定在3 300 pF、设定电阻元件参数变化分别为10 kΩ、30 kΩ时扫描,仿真Output选择为观测信号源、电阻电压和电容电压波形。实现参数扫描仿真波形如图2所示,图中波形为:①方波输入;②③电阻为10 kΩ、30 kΩ时电阻输出;④⑤电阻为10 kΩ、30 kΩ时电容uC输出。
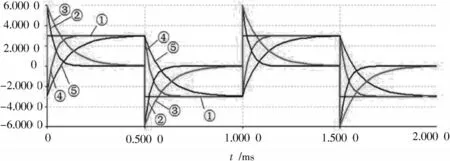
图2 电阻参数扫描时所有输入/输出电压波形
由图2可以看出,任何时刻都满足KVL,即在10 kΩ时②+④的波形,在30 kΩ时③+⑤均等于输入①的波形。②③电阻电压为激励的微分,在±3 V换路瞬间发生跃变,出现为尖峰脉冲,电阻越小,波形越尖锐。④⑤电容输出在换路瞬间无跃变,充放电分别为-3 V→3 V和3 V→-3 V,t越小,上升或下降越快,越接近于激励方波,可见其仿真与理论分析一致[8]。
将uC波形拉开取uC(τ)=0.792 V时,即测量对应的时间常数τ。
2.2 积分电路仿真测试
方波信号源参数同上,积分电路选择参数若为R=30 kΩ,C=0.33μF,τ=RC=9.9 ms,电容电压输出为激励的积分。
用Multisim参数扫描仿真,电容不变,电阻分别为10 kΩ和30 kΩ扫描,输出波形如图3所示,①②分别为电阻10 kΩ、30 kΩ时电容输出,可以看出,τ越小,积分速度越快,上升和下降越陡,与理论分析一致[9]。
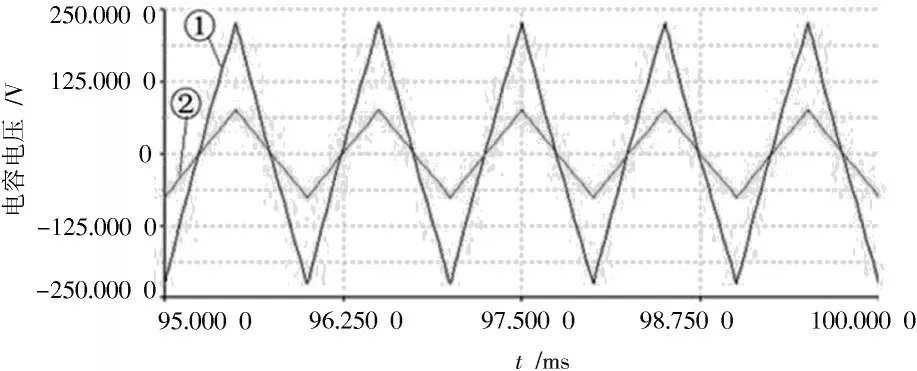
图3 电阻参数扫描时电容输出波形
由图3可见,Multisim仿真功能强大,同时可观测电路中电源输入、各个元件输出及不同参数的动态电路响应,全面直观地显示了脉冲激励下暂态过程的规律。
3 正弦激励下的暂态过程仿真测试
在Multisim下构建图1电路中,信号源取正弦信号,其参数为Usin=30 V,f=1 kHz,则激励为uS=30 sin(ωt+φS)V。选元件参数R=2 kΩ,C=1μF,由此得时间常数为τ=2 ms,由前面理论分析代入式(5)得电容电压稳态幅值UCm=2.38 V。
在Multisim中选择瞬时分析(Transient Analysis),在Analysis Parameters选项中的Initial Conditions下拉菜单中,选择User-defind,每次仿真分析前,要设定电容器的初始条件[10],下面为过电压仿真测试。
1)若uC(0+)=0 V,φC=±90°,由式(8)、式(9)得信号源初相和电容电压:
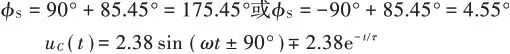
uC(t)是两个倒相的正弦函数分别与指数函数的叠加。
当φC=90°,φS=175.45°,采用Multisim的Transient Analysis实现仿真,结果如图4所示。由图4游尺读数,当t=0.458 51 ms时,即接近半个周期时,电容电压为-4.175 7 V,在近似5τ时,暂态过程结束,达到稳态值2.313 4 V,过电压最大值是稳态时幅值的1.8倍。当理论 计 算 时,取t=0.458 51ms,uC(0.458 51)=-4.19 V。同理可得φC=-90°,φS=-4.55°仿真,其与图4波形倒相,取t=0.458 51 ms,uC=4.19 V。可见仿真与理论一致。
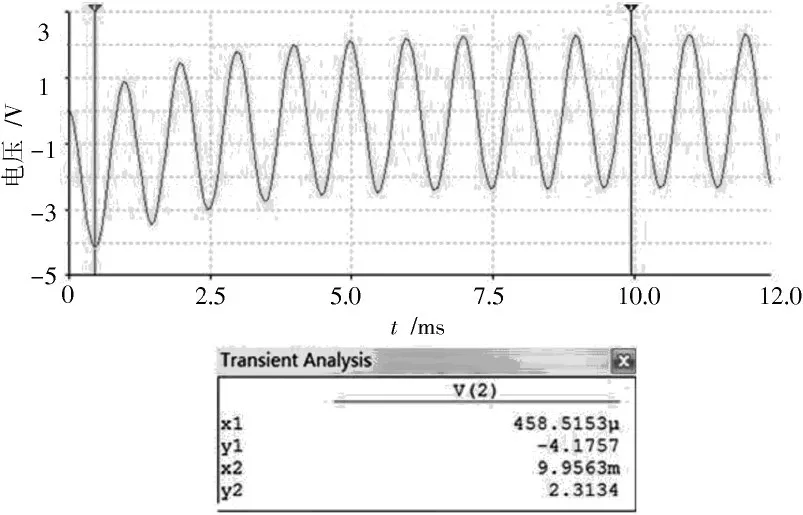
图4 当uC(0+)=0 V,φS=175.45°时过电压测试
2)取u(0+)=UCm,φC=-90°,此时可以由式(6)得φS=-4.55°,由 式(10)可 得uC(t)=2.38 sin(ωt-90°)+2×2.38e-tτ,仿真结果如图5所示,由仿真可见在接近半周期处,即游尺读数在t=0.450 928 4 ms时出现最大值6.067 2 V,超出了稳态幅值的2倍多,在近似5τ时,达到稳态值2.371 3。当理论计算时,取t=0.450 928 4 ms,得uC(0.451)=2.549UCm=6.067 V,可见仿真结果与理论一致。
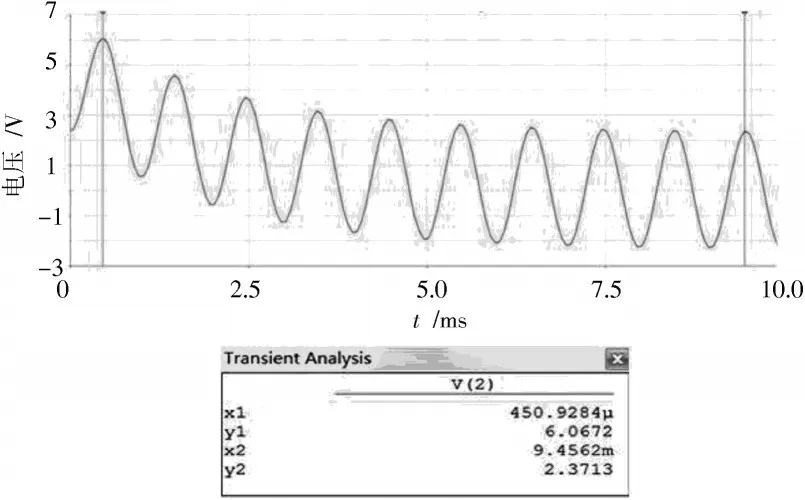
图5 u(0+)=UCm,φS=-4.55°过电压测试
由图5可知,Multisim仿真实现了正弦激励下的暂态过程测试,清晰可见过电压的发生,当电路参数和初始值一定时,过电压发生与初相φS有关,不同时刻合上开关,信号源初相φS会不同,当满足一定条件时,会发生过电压,实际工程中应予以规避。
4 结 语
通过现代Multisim电子电路仿真技术研究一阶动态电路的暂态过程,可以看到Multisim仿真解决了传统实验室研究的弊端,仿真研究比实际测试的功能齐全、测试方便,可以全面直观地研究一阶电路暂态过程的变化规律。该一阶电路的仿真研究可以使得更加有效利用暂态过程的变化特性,如应用微分、积分电路获得多种需要的波形;正弦激励下的暂态过程测试弥补了实验室不能测试缺陷,可以有效避免过电压产生的危害,这在工程上有着十分重要的意义,如在接通空载电缆时,应避免过电压的产生。
仿真结果表明,Multisim对一阶电路的研究准确全面、方便直观、效果理想,Multisim仿真对电路设计和测试提供了一种有效的方法和手段。

