磁控二氧化钛忆阻混沌系统及其电路设计

许向亮,李国东,2,戴婉莹

(1.新疆财经大学 统计与数据科学学院,新疆 乌鲁木齐 830012;2.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

1971年,Chua首次提出忆阻器是一种磁通与电荷相关的元件[1]。2008年,惠普公司的研究人员首次在实验室做出忆阻器实物[2],并在后续实验得出了忆阻器的记忆原理[3],忆阻器的阻值是流经它的电荷所确定的。纳米忆阻器的出现,有望实现非易失性随机储存器。由于纳米忆阻器的随机储存器的集成度、读写速度、功耗较传统随机储存器更为优越,得到了研究人员的广泛关注,目前已有大量的文献对荷控型和磁控型忆阻器的数学模型[4-8]以及忆阻混沌系统的SPICE模型[9]进行了报道,但是这些模型并不能较好地应用于实际电路,因此建立了各类相关忆阻器的替代模型和等效电路,分别采用离子迁移、压控忆阻器等方法实现混沌电路的双稳性[10]和语音信号的保密通信[11]。在以上所述的研究成果中,基于磁控制构建的仿真器并不常见,基于磁控模型的忆阻电路是未来构建复杂混沌系统的趋势,因此,研究磁控忆阻器模型具有重要意义。依据忆阻器原理,构建二次、三次、分段非线性模型忆阻器引入传统混沌系统,如Lorenz系统[12]、蔡氏混沌电路[13]、多涡卷Jerk系统[14]、文氏电路[15],丰富了构建忆阻混沌系统的方法。近年来,在传统混沌的基础上提出了许多基于磁控二氧化钛忆阻器的混沌系统[16-18],当系统出现多稳态[19]现象时,其具有复杂的拓扑结构和动力学行为,可用于图像加密[20]。且随着忆阻混沌系统在通信保密领域的广泛应用,系统参数的选择显得尤为重要,系统参数的选择会影响混沌信号的伪随机性。本文尝试采用混沌图和复杂度分析结合的方法得到了系统的最优参数,该方案具有普适性,便于广泛推广。

本文提出了一种结构简单的忆阻混沌系统,采用磁控二氧化钛忆阻器来构建混沌系统的非线性项,详细地分析了该系统的动力学行为。系统存在特殊的分叉结构,双层分叉或者类周期性窗口可以保证系统的混沌特性,在分叉断层区间,系统的Lyapunov指数较小,采用混沌图、复杂度分析等方法能够得到该区间混沌系统的最优参数取值范围,且在最优参数范围控制下的忆阻混沌系统,其多稳态共存现象更加显著,从而验证了该系统可以产生丰富的动力学行为,并用Multisim实现了该系统的混沌电路仿真,其实验结果验证了数值仿真的正确性。

1 磁控二氧化钛忆阻器混沌系统及其动力学分析

1.1 基于磁控二氧化钛忆阻器的混沌系统模型

本文提出的一种带有磁控二氧化钛忆阻器的混沌系统,其状态方程描述如下:

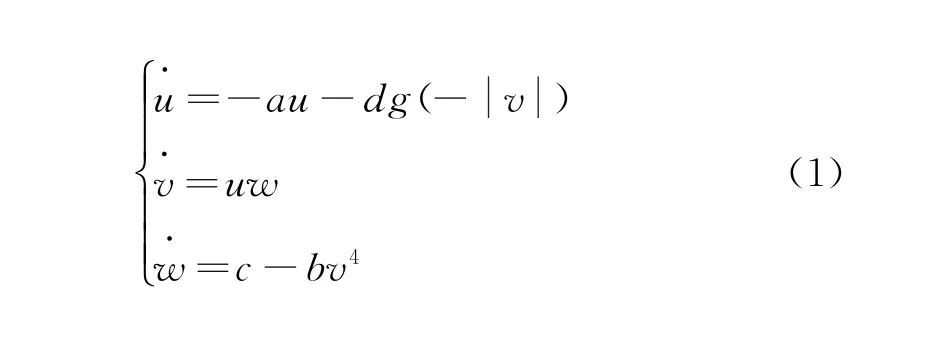
式中:u,v,w∈R为该忆阻混沌系统的状态变量;a,b,c,d为系统参数;g(·)为系统的非线性项。磁控二氧化钛忆阻器的电荷编码[9]如下:

式中:v表示输入忆阻器的磁通;RON和ROFF分别代表忆阻器的两个极限值;M(0)为忆阻器的初始值;k=[(RON-ROFF)×μvRON]/D2,其中D是薄膜厚度;μv是所用忆阻器模型中氧空位的平均迁移率。设置忆阻器的参数如下:RON=100Ω,ROFF=20 kΩ,M(0)=15 kΩ,μv=10-14m2·s-1·V-1,D=10 nm,当系统的初始状态(u,v,w)=(0.6,0.2,0.3)时,参数a=6,b=8,c=50,d=105,该系统处于混沌状态。设置时间为10 s,采用龙哥库塔法利用Python3.7对系统(1)进行仿真,得到管状3D图。系统在保留初始状态的基础上添加微小改动,呈彩色状分布,分别得到u-v平面、u-w平面、v-w平面的相图,如图1所示。

1.2 忆阻混沌系统的动力学分析

1.2.1 对称性分析与耗散度分析

由系统(1)的相图可知,系统存在对称性,即(u,v,w)→(-u,-v,w),系统保持不变,关于w轴对称,它满足f(PT)=Pf(T),其中R表示三个维度,T表示系统(1)的状态方程,P为变换矩阵,其变化可表示为:

图1 系统(1)的混沌吸引子。(a)u-v平面;(b)u-w平面;(c)v-w平面Fig.1 Chaotic attractor of system(1).(a)u-v plane;(b)u-w plane;(c)v-w plane

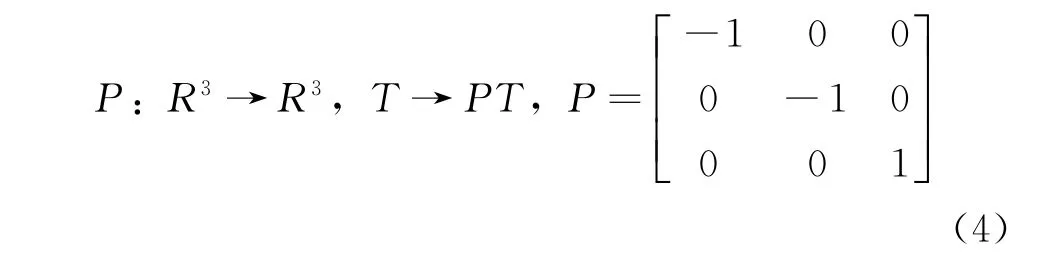
系统(1)的耗散度计算如下:

当系统(1)的参数a＞0,此时系统是耗散的,系统(1)是有界的,其轨道变化收缩率为:

也就是说一个初始值状态下为V(0)的体积元在t时刻收敛速度为e-a,当t→∞时,系统运动轨迹上的每一个微小体积元都将以e-a指数倍速率快速收敛到零,本文选取系统的参数为:a=6,符合上述形式,该系统运动的轨迹线,最终会被控制在一个体积为零的极限集合,渐进运动吸引到固定的值上,说明该系统存在吸引子。

1.2.2 平衡点的稳定性

为了求解系统(1)的平衡点,令系统(1)变为齐次状态方程。即:

令a=6,b=2,c=50,d=105,此时系统有三个平衡点:S1(0,0,0),S2(2.2361,2.2361,0),S3(-2.2361,-2.2361,0)。

系统(1)的线性化Jacobian矩阵为:

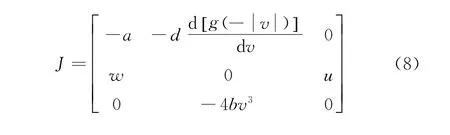
令系统(1)特征方程det(J-λI)=0,系统在平衡点S1(0,0,0)处的特征根λ1=1.4536,λ2=-1.2145,λ3=-7.2254。其中因为λ2,λ3为负实数根,λ1为正实数根,所以系统平衡点S1(0,0,0)是一个不稳定的鞍焦点。

在平衡点S2(2.2361,2.2361,0)处的特征根λ1=1.5811,λ2=1.4571+0.9823i,λ3=1.4571-0.9823i;λ2,λ3为一对共轭负数根,λ1为正实数根,所以系统平衡点S2(2.2361,2.2361,0)是一个不稳定的鞍焦点。

在平衡点S3(-2.2361,-2.2361,0)处的特征根λ1=1.5811,λ2=1.4571+0.9823i,λ3=1.4571-0.9823i;λ2,λ3为一对共轭负数根,λ1为正实数根,所以系统平衡点S3(-2.2361,-2.2361,0)也是一个不稳定的鞍焦点。

1.2.3 Lyapunov指数谱和维数

Lyapunov指数是衡量非线性动力学系统特性的一个重要的定量指标,它计算了相空间中相邻运动轨道间收敛或发散的平均指数率,且一个正的Lyapunov指数意味着在系统的相空间中相邻两条轨道之间的差别随时间的演化而呈现指数级分离且无法预测。设置系统(1)的初值状态为(u,v,w)=(0.6,0.2,0.3),且设置系统参数为a=6,b=8,c=50,d=105,选取时间t=300 s,采用雅可比矩阵的方法得到如图2的Lyapunov指数谱,该系统具有一个正的λ1=1.133,一个趋近于0的λ2=-0.0099968,一个负的λ3=-7.1222,且满足λ1+λ2+λ3＜0,此时该系统处于混沌状态。

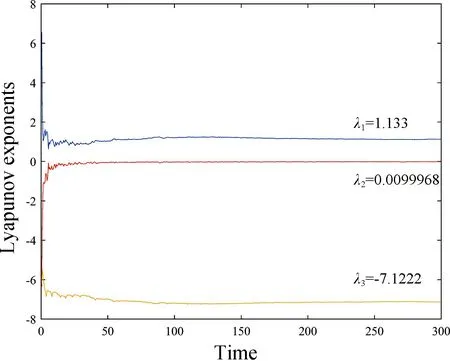
图2 系统(1)的Lyapunov指数谱Fig.2 Lyapunov exponential spectrum of system(1)

依据Yorke公式计算Lyapunov维数:

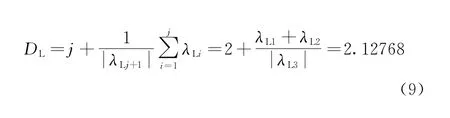
系统(1)出现分数维,此时系统处于混沌状态。

1.2.4 功率谱和庞加莱截面

当系统(1)参数a=6,b=8,c=50,d=105时,取(u,v,w)初值状态为(0.6,0.2,0),t=2000 s时,图3的(a)、(b)分别为该系统的功率谱和庞加莱截面。其功率谱图具有连续尖峰和噪声背景的特征,从而验证此系统为混沌系统,此外,Poincare截面映射保持了原系统的周期和准周期轨道的许多特性,且具有低维状态空间。从系统(1)的Poincare截面映射呈现出成片的具有分形结构的密集型连续点,与其他系统不同的是,该系统的吸引域呈现旋转形状,且在最外层出现分段现象,因此该系统可能存在多稳态共存的现象。

1.3 分叉图

1.3.1 双分叉区域分析

设置系统参数a=6,c=50,d=105,令b为控制变量,控制区间为 [0,50],步长为0.05,初始状态(u,v,w)=(0.6,0.2,0.3),其分叉图如图4所示。

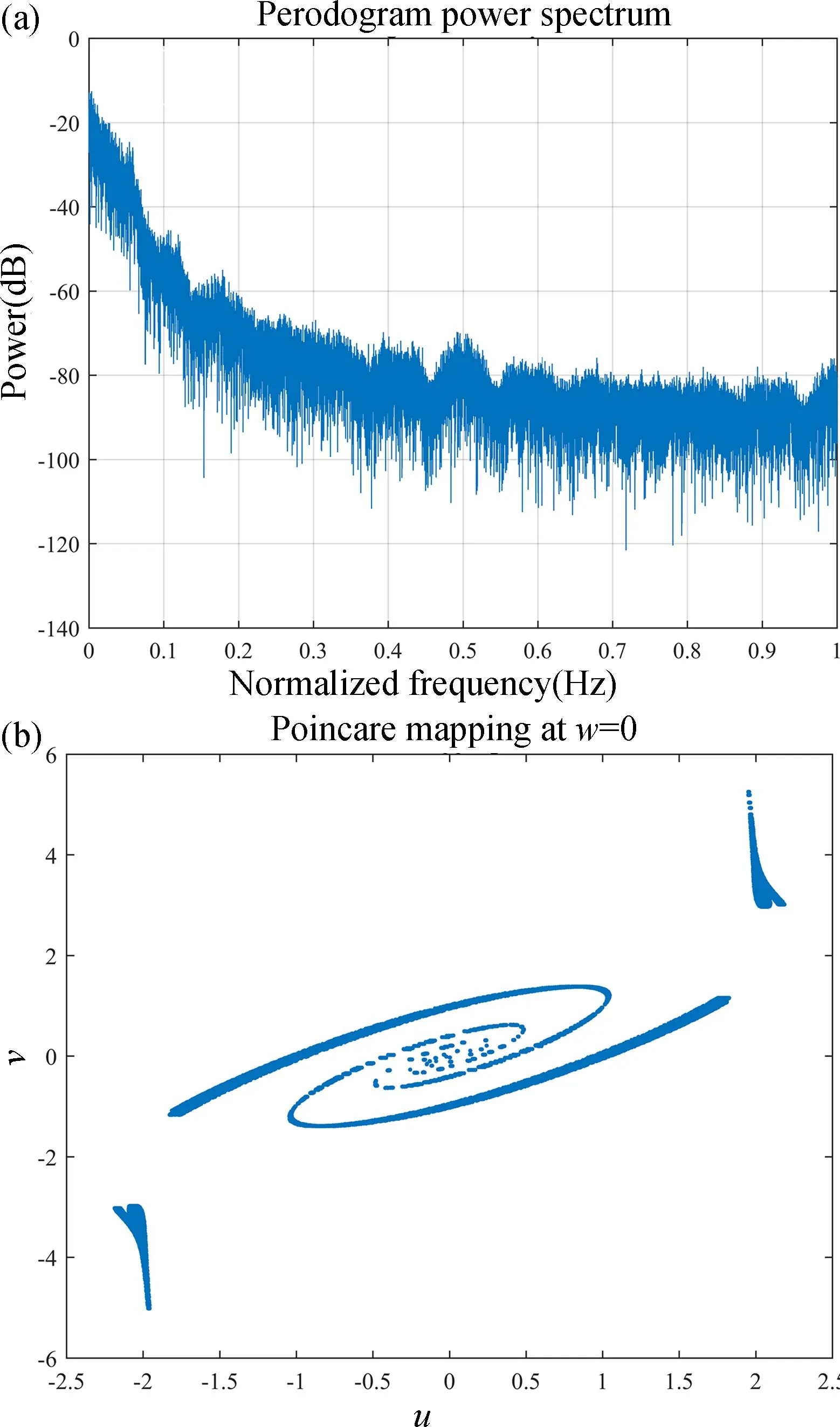
图3 系统(1)的功率谱和庞加莱截面。(a)功率谱;(b)庞加莱截面Fig.3 Power spectrum of system(1).(a)The power spectrum;(b)The Poincare map

图4 系统(1)的分叉图Fig.4 Bifurcation diagram of system(1)

其分叉图呈现分区域状态,出现双分叉现象,其中上层比下层的点数密集,因此参数在该区域的取值不会影响混沌的状态,此时混沌的轨道仍会呈指数级分离,不会向单轨道迁移。在区间 [6,15],对分叉图进行放大处理,混沌分叉出现自相似性,仍旧出现分叉断层现象。

1.3.2 分叉断层区域分析

为了进一步探究混沌轨道是否会在此区域出现单轨道迁移,采用1.3.1中设定的系统参数,在分叉图的放大区间保留两种初始值状态(参考表1)进行作图,由图5(a)可知:在同一参数下,不同初始状态的分叉图也存在着差异,且无论是红色或是蓝色均在b=11右侧出现断层现象。将蓝色状态下的分叉图剥离开来,观察到蓝色初值状态下的参数b→11的时候出现明显的分叉断层现象,如图5(b)所示。

图5 分叉图。(a)不同初始值状态;(b)单一初始值状态Fig.5 Bifurcation diagram.(a)Different initial value state;(b)Single initial value state

在传统的混沌分叉区域分析中,混沌分叉会呈现周期分叉,伴随着混沌轨道呈现周期现象,此时系统不混沌。系统(1)的分叉不仅具有周期性、双层分叉性,而且出现了其他系统没有的分叉断层区域,分叉断层意味着混沌周期性消失,此时系统不再具有混沌特性,蓝色分叉图在区间b=[11,12]出现类周期现象,具有4个类周期窗口,且在第三个类周期窗口出现分叉断层(图5(b)黑色椭圆区域),因此判断分叉断层区可能会对混沌系统产生影响,为此本文从该区域的Lyapunov指数谱图6(a)和最大Lyapunov指数图6(b)进行探究。

图6 Lyapunov指数。(a)Lyapunov指数谱;(b)最大Lyapunov指数Fig.6 Lyapunov index.(a)Lyapunov index spectrum;(b)Maximum Lyapunov index

设定参数b的范围为 [10.5,11.5],步长为0.05,从图6(a)的Lyapunov指数谱可以看出在参数b=11,正的Lyapunov出现急剧下降,且在b=11.34左右达到最低点,此时Lyapunov=0.2663。为了更好地体现分叉断层区Lyapunov指数的变化状况,采用奇异值分解法来求解该区域系统的最大Lyapunov指数,如图6(b)可以反映出参数b=11时,系统的最大Lyapunov指数急剧下降的现象更加明显,且持续时间较长,与参数在b=[5,6]时的混沌类周期窗口相似,由于此区域还有别的类周期窗口,混沌轨道不会出现周期性变换,更不会出现相近轨道最终会靠拢合并为一点,但是此时系统的Lyapunov指数减小,混沌特性不够明显,混沌程度也会减小。因此可以得出一个结论:当混沌系统出现单一分叉断层时,多层分叉或者类周期窗口可以保证系统的混沌特性。

1.4 混沌图和复杂度分析

由于该忆阻混沌系统存在分叉断层行为,且最大Lyapunov指数急剧下降,那么找出该系统的最优参数范围显得尤为重要。采用双参数影响下的混沌图和复杂度分析相结合的方法来选取混沌系统的最优参数范围。混沌图是在参数空间中反映混沌系统动力学的一种综合方法,系统的参数应该选择在复杂度较高的区域;测量复杂度的方法有频谱熵(SE)、C0熵和排列熵(PE)[21-23]。其中,PE算法是准确、快速估计数值序列的正确选择。因此,采用排列熵(PE)算法分析了在b参数范围下混沌系统的复杂性,PE值越大,时间序列越复杂。

从图7(a)双参数影响下的混沌图可知:系统参数b∈(7.5,11)、a∈(0.4,1.1)区间的混沌信号的复杂度几乎接近1,基本符合参数b范围下的混沌复杂度分析,系统参数在此范围下可以达到最优,此时,混沌信号的随机性更强,更适用于安全通讯领域。

图7 最优忆阻混沌系统参数。(a)混沌图;(b)PE复杂度分析Fig.7 Parameters of optimal memory chaotic system.(a)Chaotic diagram;(b)PE complexity analysis

1.5 最优参数范围下的多稳态共存分析

多稳态是指系统拥有的不同稳定运行状态,且会随着时间在两个或几个互斥的状态之间切换,在混沌系统中有大量不同轨迹共存的特殊形式,多稳态系统很容易受初始条件的影响。表1提供了不同初始状态下系统多稳态共存的参数。

在最优参数范围下系统存在多稳态共存现象,给定系统(1)的参数,分别设定系统的初始状态,时间为5 s,如图8(a)显示:初始状态(u1,v1,w1)为蓝色轨道,(u'1,v'1,w'1)为红色轨道,此时混沌的吸引域形成,且系统出现多稳态共存现象。设置时间为15 s,如图8(b)显示:初始状态(u1,v1,w1)为红色轨道,(u'1,v'1,w'1)为蓝色轨道,此时两个双涡卷忆阻混沌系统轨道会出现指数级分离,红色轨道主要聚集在左涡卷区域,蓝色轨道在左右涡卷吸引域产生聚集,系统的多稳态共存现象更加显著。

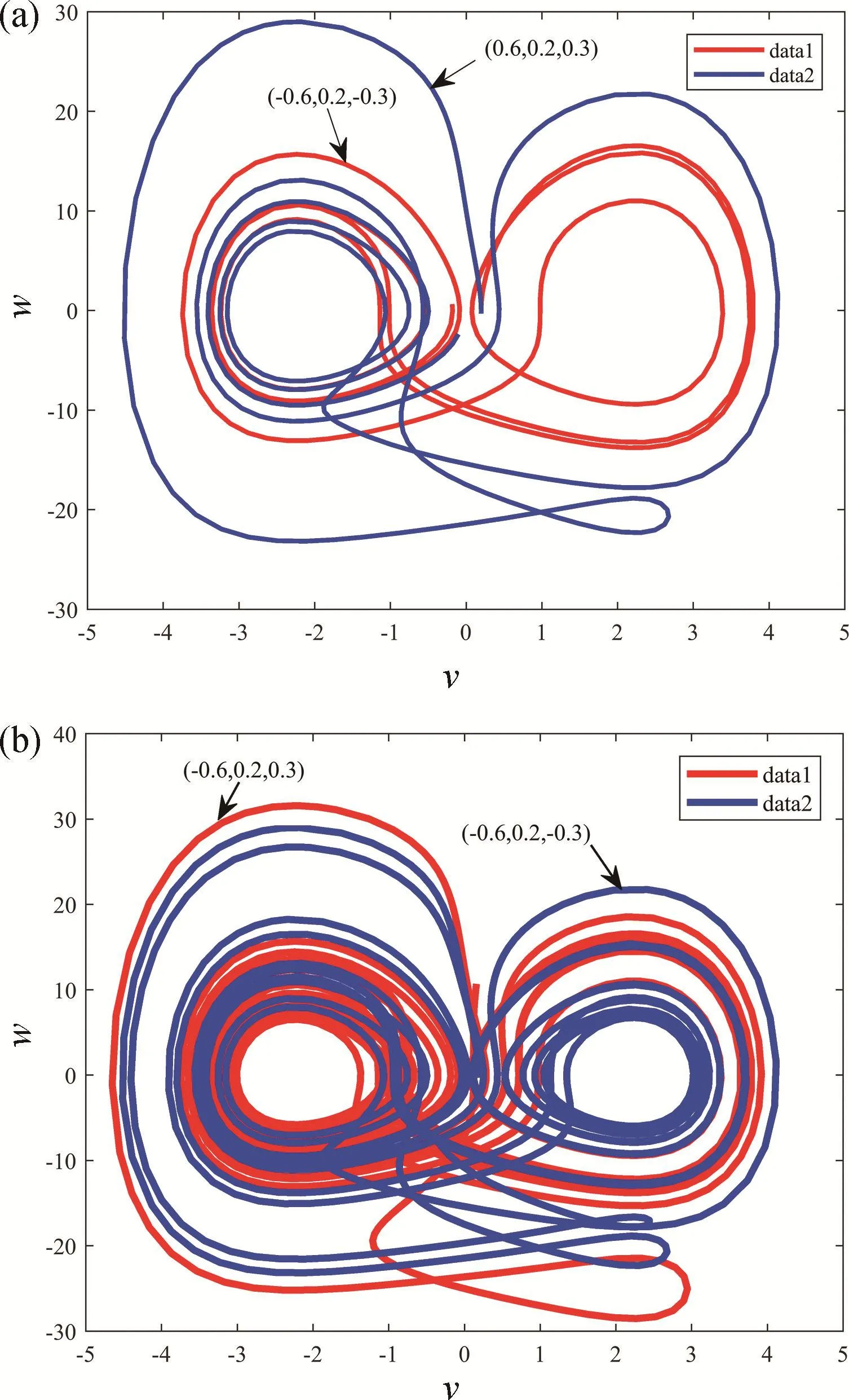
图8 v-w平面的多稳态共存。(a)t=5 s;(b)t=15 sFig.8 Coexistence of multiple steady states in v-w plane.(a)t=5 s;(b)t=15 s

从上述系统的多稳态现象可以反映出,系统在最优参数范围控制下,随着迭代次数的增加,系统的多稳态共存现象也更加明显,表明在最优参数范围控制下,该忆阻混沌系统具有丰富的动力学行为。

表1 多稳态共存参数Tab.1 Multi-steady-state coexistence parameters

2 基于Multisim的忆阻混沌电路实现

Multisim提炼了SPICE仿真的复杂内容,并对电路进行捕获、仿真和分析新的设计,通过Multisim和虚拟仪器技术,可以完成从理论到原理图捕获与仿真,再到原型设计和测试这样一个完整的综合设计流程。除此之外,虚拟的模拟元器件容易受到环境的温度、湿度以及元件器老化等条件的约束,Multisim具有丰富的元器件来提供电路的配置。由于文中的忆阻器中含有开方运算,因此要采用改进的电路模块化设计方案[24],使用Multisim14.0版本搭建忆阻混沌系统的电路。

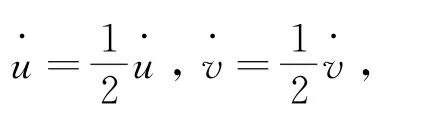
图9 磁控二氧化钛忆阻混沌电路原理图Fig.9 Schematic diagram of a new double vortex memristor chaotic circuit

其状态方程为:

在图9中,R1,R2的电阻值为66.67 kΩ,R3,R4,R5,R6,R8,R9的电阻值为100 kΩ,R7的电阻值为32 kΩ,C1=C2=C3=1μF,电源元器件V1=-1 V,对于含有忆阻器模块,元器件R10=16 kΩ,C4=10μF,C5=10 nF,R11=10 kΩ,电路中采用模拟乘法器Multiplier,运算放大器采用TL082CD,电源电压为±15 V,从而实现系统中非线性乘积项的乘法运算。蓝色框采用双乘法器模拟v2v2中的双乘法运算,黑色椭圆区域采用负电压反向控制模拟常数项,绿线框内为构造的磁控二氧化钛忆阻器。图10为系统(1)的电路仿真结果。示波器显示的仿真结果与数值仿真的结果一致,验证了该忆阻混沌系统在物理上实现的可能性。

3 结论

由于忆阻器尺寸较小、能耗低,在混沌电路中有着较高的应用价值,本文将磁控二氧化钛忆阻器作为混沌系统的非线性项,提出了一种基于磁控二氧化钛的新型双涡卷忆阻混沌系统,详细地分析了系统的复杂动力学行为,设计了该忆阻混沌系统的模拟电路,并进行了仿真,得出如下结论:

(1)该忆阻混沌系统出现分叉断层现象或者类周期性窗口时,系统的双分叉可以保证系统的混沌特性,但是此时的Lyapunov指数会急剧减小,系统的混沌特性会降低。

(2)采用双参数影响下的混沌图和复杂度分析结合的方法,可以得到分叉断层区间系统的最优参数。

(3)在最优参数范围下的忆阻混沌系统,系统多稳态共存现象显著,具有丰富的动力学行为。

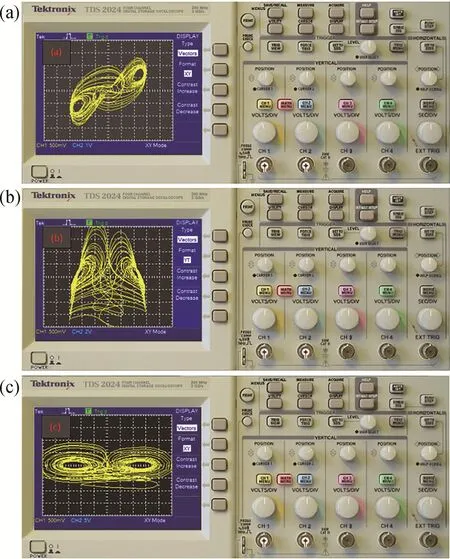
图10 示波器显示系统(1)的相图。(a)u-v平面;(b)u-w平面;(c)v-w平面Fig.10 Phase diagram of oscilloscope display system.(a)u-v plane;(b)u-w plane;(c)v-w plane