矢量叠加初至波定位方法及精度评价

杨海申 徐丽军 马 洁 侯昆鹏 肖永新

(东方地球物理公司采集技术中心，河北涿州 072751)

0 引言

在海上勘探中，无论是OBC还是OBN勘探，检波器都是通过抛掷或机械方式放置于海底，电缆或节点检波器在到达海底过程中因受海流[1]、潮汐[2]、船速以及检波器沉降速度的影响而偏离设计位置。而实时导航提供的测量资料只是检波器离开放缆船到达海面的位置(一次定位点)信息，检波器在海底的实际位置与导航结果存在一定偏差，因此必须通过某种方法得到检波器在海底的实际位置[3]。厘清检波器在海底的准确位置，能提高后期资料处理和解释的可信度[4]，二次定位技术正是在这种需求下应运而生的。对检波点进行二次定位的现行主要方法是声波定位法和初至波定位法[5]。

声波定位方法需专用声学检波器接收由声波发生器发出的声学信号，然后利用圆圆定位原理进行定位[6-10]，其特点是需用专项设备和专用施工流程，采集费用高，施工效率低，在浅水域数据采收率低，最大接收距离通常小于1000m，但其计算精度高，在前期海上勘探中应用较多。

初至波定位方法则是利用地震记录初至时间进行定位[11]，不需专用声纳设备及施工流程，利用常规采集地震数据，通过拾取的初至计算检波点位置[12]。与声波定位相比，采集费用低、定位效率高，应用更为普及。经过多年发展，初至波定位方法衍生出多种方法，定位精度也在逐步提高[13-14]。按初至波定位方法的原理可分为初至波圆圆二次定位法[7，15-16]、折射波二次定位法[17-18]、网格扫描定位法[19]、直达波折射波二次定位法[20-21]和扫描拟合定位方法等五种。但各种方法又有其自身特点和限制，如初至波圆圆定位法计算效率较低，折射波法适用于折射波发育、有稳定折射层的探区，网格扫描法的定位范围受网格范围限制等[7，15-21]。

本文在充分调研上述诸多算法基础上，提出一种新的初至波定位法——矢量叠加方法。该方法通过构建每个炮检对的位置矢量，并进行矢量叠加，得到检波点的准确坐标位置，并给出定位精度的量化评价指标，形成了一套从初至拾取、定位计算到定位精度评价的完整的高精度定位方法。

1 矢量叠加定位方法原理

假设某检波点初始坐标为(x0，y0，z0)，已知第i个炮点的坐标为(xi，yi，zi)，则检波点到炮点的理论炮检距为

(1)

此时该检波点的初至时间为ti，海水速度为v，则传播路程(即实际炮检距)为

Wi=vti

(2)

定义向量Di，其模为实际炮检距Wi减去理论炮检距Ri的差的绝对值|Wi-Ri|。若Wi-Ri大于零，则向量方向从炮点指向检波点； 若Wi-Ri小于零，则向量方向从检波点指向炮点。

将第i个炮检对的矢量记为Di，则每个炮点都可形成一个向量，称为残差向量，如图1所示。

图1 矢量叠加原理示意图

对检波点与每个炮点的残差向量Di求和，得到总矢量D。检波点按矢量移到新位置，得到初至波定位新坐标，总矢量方向和即为检波点移动方向，总矢量大小就是检波点移动距离。显然有

(3)

式中n为与该检波点对应的炮点数。

在实现过程中，需进行多次迭代计算，检波点逐步逼近准确位置。图2显示某检波点迭代收敛过程，可见经10次迭代后，收敛误差达到0.1m。实际的初至数据、速度及炮点坐标都会有误差，定位精度也受其一定影响。利用理论数据计算，该方法定位精度可达毫米级以内。

图2 矢量叠加迭代收敛曲线

严格地说，矢量叠加定位法也属于圆圆定位法的一种，只是实现方式不同。一般要求前提条件是至少有三个炮点，且处于不同方位。若炮点位于同一直线或集中于一个方位，对应的矢量图也会集中于一个方向，虽能快速收敛，但可能会造成在其他方位定位坐标不准确，从而导致整体定位精度降低。对于三维勘探，一般都能满足此条件。通过构建不同方位的残差向量，再根据矢量和定位检波点位置(图3)。

图3 三维勘探炮点分布示意图

该定位方法能适应空间上的变化，即对x、y、z三个方向的坐标进行定位。基于现行施工方式，气枪激发位置大体处于同一深度面，导致对z坐标的定位欠准确。为弥补此缺憾，可按定位后的(x，y)坐标，从海底面高程中得到新的z坐标。

2 速度的计算

定位计算需首先求取初至波速度。在较深海域，初至波即是沿海水传播的直达波(图4b)。但对于浅海区域，较大炮检距的初至波往往是来自海底的透射波或折射波。随着炮检距增大，初至波速度逐渐增高，初至—炮检距关系表现为曲线(图4a)。

图4中的横坐标炮检距由炮点和检波点坐标计算得到，纵坐标为经线性动校正(LMO)后的初至时间。对初至点进行曲线最小二乘拟合，曲线斜率的倒数即是初至波的速度。具体实现中，将炮检距分为若干段，计算每一段的平均速度，得到随炮检距变化的速度场。由于检波点坐标位置存在偏差，得到的初始速度也是有误差的。在矢量叠加迭代过程中，随着检波点坐标位置的修正，速度也需重新计算和更新，这样才能保证最终定位精度。

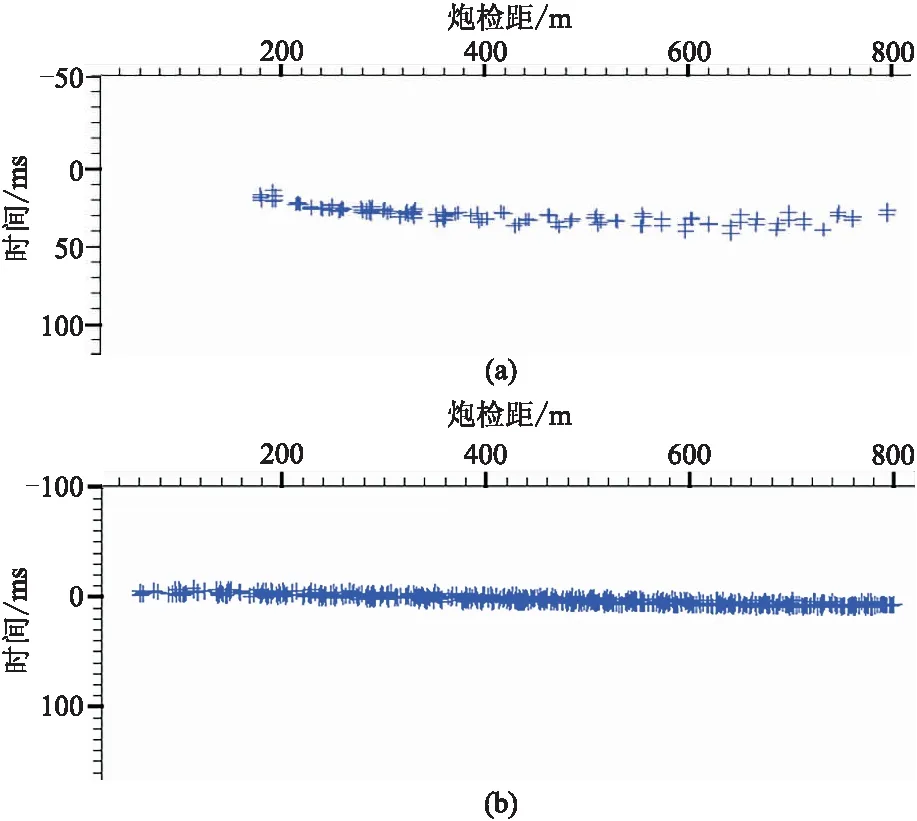
图4 浅海(a)和深海(b)区域的初至分布

在本文方法实现中，对多个检波点的初至同时进行拟合，以保证足够数据量及速度值的稳定。另外，应选择近炮检距范围(0～500m)参与计算，避免出现随炮检距的变化速度产生较大变化。

3 坐标初始值对定位的影响

为考察定位方法的稳定性及对初始坐标的依赖性，选择M海域节点实际资料，给定偏离20m后不同位置初始坐标做定位计算。经测试，定位后坐标都能收敛到一个固定值(表1、图5)。分析定位后坐标(图6)，其最大位置差仅约为0.15m，可认为不同初始坐标对定位结果的影响为±0.075m。对于现行勘探精度要求，此偏差可忽略不计。

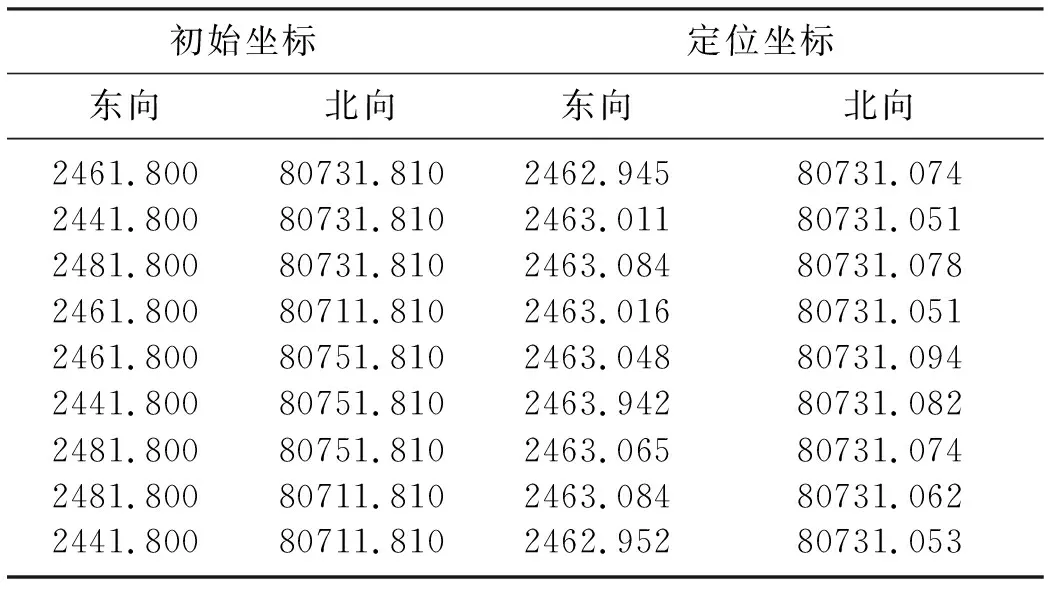
表1 不同初始坐标的定位结果 单位：m

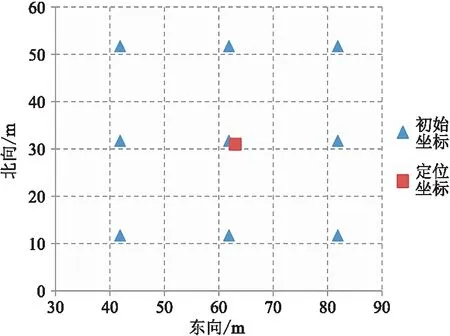
图5 初始坐标与定位后坐标平面分布图

图6 不同初始坐标的定位计算结果平面分布

4 定位精度的评价

对定位精度的评价有三种常用方式。一是对道集进行LMO，观察初至是否“拉平”，是一种定性评价方式。LMO与使用的速度有关，当初至速度随炮检距变化时，准确的速度不易给定； 而且“拉平”效果也是定性的，无量化指标。二是查看异常值是否过多，整体偏差性趋势是否明显[22]，这也是一种定性评价方式。三是与声波定位对比。一般认为声波定位结果是准确可靠的，若初至波定位结果接近声波定位结果，就可认为该初至波定位结果是准确的。此方式须有专用设备和额外的施工流程，不易推广。

本文提出两种定位精度量化评价方法，可计算三种量化属性，用于对定位精度进行量化评价。另外，残差向量分布、初至分布等图件，也可定性地评判检波点坐标位置精度。

4.1 叠加能量

以正确炮检点位置和合适速度进行LMO，初至可被拉平。对于校正后道集，在初至附近选择一个时窗，对时窗内道集进行同向叠加，可得到最大能量值。若检波点位置不正确，LMO后道集不能被拉平，此时叠加能量小于最大值。因此，根据叠加能量，可判别道集的拉平程度。但叠加不仅能反映检波点位置的偏差，也与LMO速度有关。当采用有偏差的速度时，LMO后的道集会呈周期性对称起伏变化(图7a)，其对应的叠加能量也不能达到最大值。从实际检波点道集LMO后叠加能量的对比(图7)可以看出，LMO速度若有误差，对同一炮检距道的影响是一样的，即相同炮检距道的LMO校正量一致。

图7 LMO后检波点坐标存在偏离(a)与处于正确位置(b)的道集对比

根据此原理，提出按炮检距分段叠加方法： 将炮检距分成若干段，在每段内炮检距接近，LMO后能同相叠加； 然后将各个炮检距段的能量再叠加，得到总能量，这样就避免了由LMO速度偏差造成的叠加能量减小，即叠加能量只与检波点位置有关。

检波点位置偏差与叠加能量并非单调线性关系，随位置的偏差会出现多个极值，但在准确位置附近(如±5m范围)会有一个极大值(图8)。因此，根据叠加能量可以有效判别检波点位置的准确程度，尤其是细微的坐标差别，但无法直观评判哪个位置的LMO可使道集排列更平直，此时可通过叠加能量定量判别哪个坐标位置更准确。

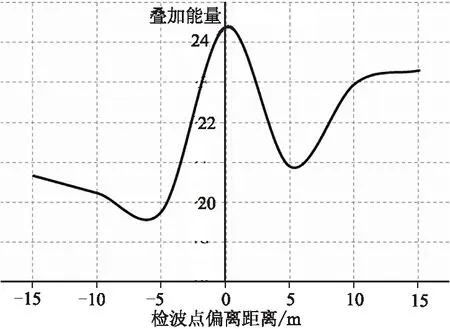
图8 叠加能量变化曲线

4.2 残差向量分布

对于实际资料，由于各种误差的存在，即使检波点坐标位置正确，残差向量仍不会为零。将检波点定为残差向量的起点，并将该点设为中心点，每一条线代表一个炮点的残差向量，绘制出各个残差向量分布图(图9)； 再根据该分布图统计出两种属性，判别坐标位置的精度。

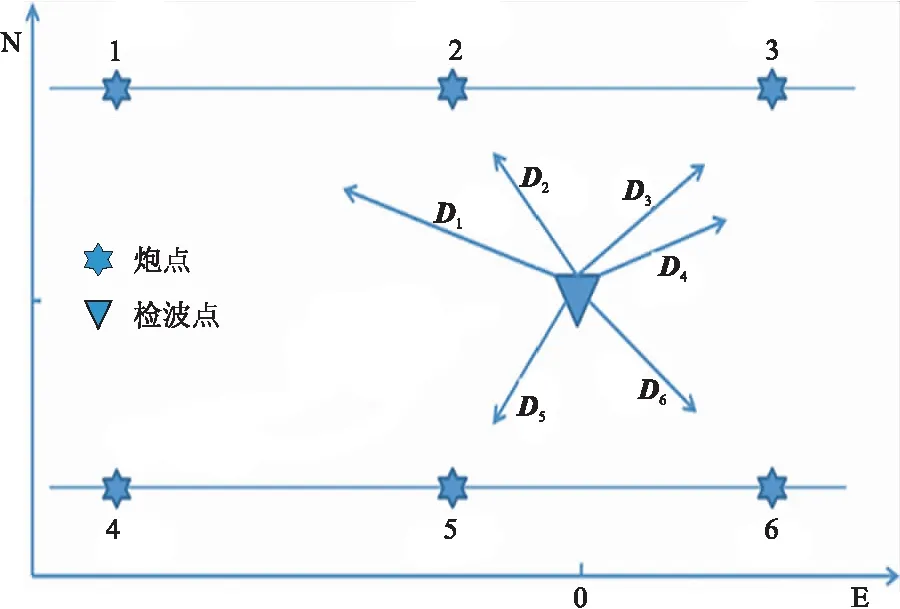
图9 残差向量分布示意图

属性一为残差向量和(δ)。所有残差向量矢量和的模为∣D∣，该值越小，定位精度越高。由于本文初至波定位法即是依据矢量和，所以初至波定位后的残差向量和几乎趋于零。但不同定位方法的该属性值不同，对于正确的初至时间，精度高的检波点坐标总是对应小的残差向量和。

属性二为离散度，是残差向量模的均方根φ。φ越小表明定位精度越高，其表达式为

(4)

图10a所示的一次定位坐标分布图中离散度为4.37，经初至波定位后(图10b)的离散度(φ)降为1.84；而残差向量和(δ)属性，由一次定位坐标的5.539骤减为初至波定位后的0.002，趋近于零，显然初至波定位后坐标位置更准确。检波点定位前、后坐标的距离是5.50m。因此，小离散度检波点位置更居中(矢量中心)，大离散度检波点位置偏离矢量中心，偏离中心点的方位基本可确定检波点坐标偏离的距离和方向。

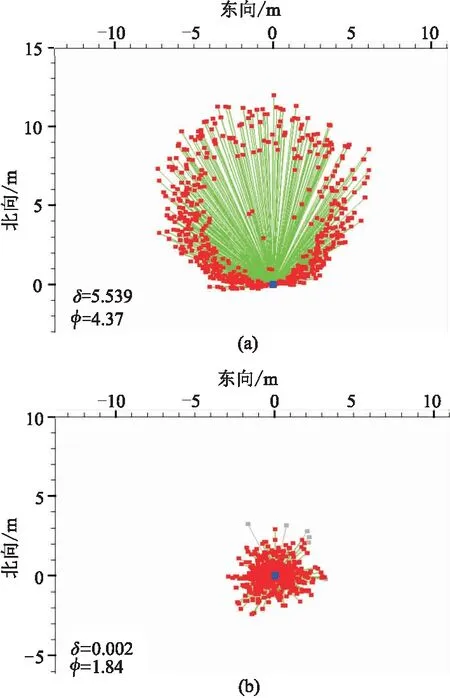
图10 实际检波点资料的残差向量分布图(a)一次定位坐标； (b)初至波定位坐标

4.3 初至分布

从不同炮检距的LMO后初至时间分布也可直观看出检波点坐标位置的定位精度。对比一次定位与初至波定位可看出，后者的初至点分布(图11b)明显变得收敛和集中了，表明初至波定位后的坐标更准确。检波点定位前、后坐标的距离是3.65m。

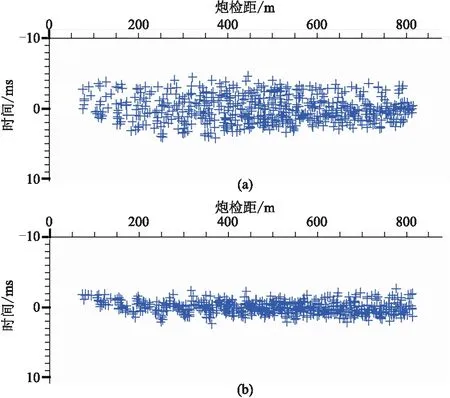
图11 一次定位(a)和初至波定位(b)坐标分布图

5 定位方法对比及定位条件分析

矢量叠加初至波定位方法在中国大港浅海区及南海某区、菲律宾海域等地区进行了测试验证，定位精度均能达到3m以内。图12为M海域施工的炮检点平面图，定位计算所用炮检距范围是0～800m，初始坐标为(已做过常规二次定位的)成果坐标，经初至波定位后，与原坐标差都在3m以内，箭头指向坐标差最大检波点。从残差向量分布(图13)可见初至波定位前、后离散度分别为3.20和2.40。初至波定位后离散度变小，检波点更居中，计算结果精度高于原成果坐标，验证了该方法的有效性。

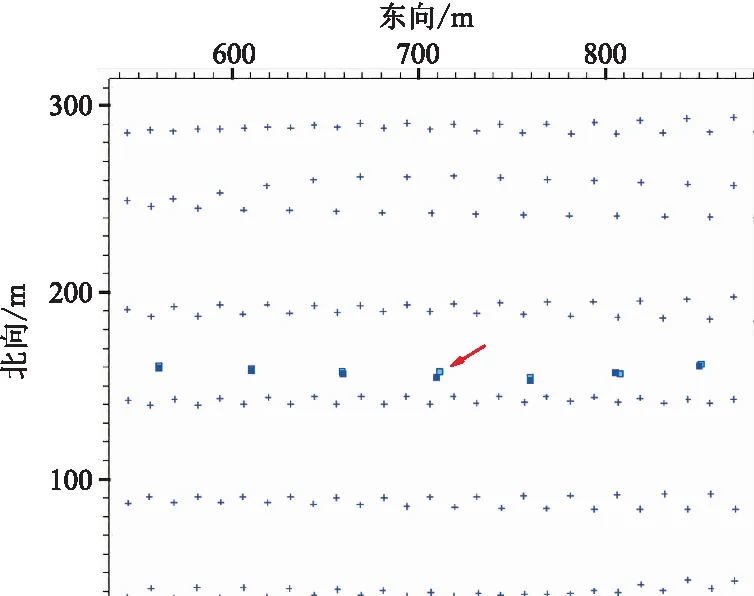
图12 M海域炮检点位置平面图

图13 M海域定位前(a)、后(b)向量分布图

进一步分析得知，除声纳定位本身误差外，时效性是声纳定位的一个弱项，声纳定位时间与气枪放炮时间存在几小时甚至一二天的时间差，在这期间检波点的飘移是造成位置偏差的主要原因。

实际应用中也发现该定位及评价方法的适用范围。当炮点位置的分布不均匀或只有远炮检距炮点等情况下，可能会造成较大的定位误差，定位精度评价也会失效，因此需首先根据资料情况确定是否满足适用条件。

图14在海外N地区的炮检点位置平面图，炮检距范围是2000～4000m，无近炮检距资料，且检波线位于炮点一侧。图15为图14中箭头所指检波点的初至波定位结果与声纳定位结果的对比，经过LMO后，虽然初至波定位能将道集拉得更平，但通过与声纳所定位置的对比，两者相差22m。虽然从叠加能量、离散度等分析，初至波定位结果的精度更高，但通过各种资料证实，声纳坐标位置是正确的。

图14 N地区炮检点位置平面图

图15 N地区声纳定位(a)与初至波定位(b)LMO对比

分析其原因，一是随着炮检距增大各种误差也随之增大，二是炮点只是分布在检波点一侧，缺少其他方位的炮点，导致定位误差急剧增大。因此，应先判定本方法的适用条件，无条件的使用会造成错误的结果。

6 结束语

本文提出矢量叠加初至波定位方法，该方法计算简单、效率高，每个检波点定位计算时间只需约5ms； 同时，提出了叠加能量、残差向量矢量和、离散度等属性，为检波点二次定位精度的评价提供了量化指标； 另外，残差向量分布、初至分布等图件，也反映了检波点的定位精度。

通过实际资料的对比，绝对定位误差小于3m，大部分节点定位误差甚至小于1m，完全满足常规施工的要求。该定位方法及精度评价方法现已形成一套完整的克浪软件产品，在印尼海上勘探Tangguh OBN项目的212万炮数据采集中，所有节点均采用了初至波定位计算，除个别节点外，绝大多数的节点定位精度高于或等同声纳定位结果。随着该方法的推广，将会在更多的项目中发挥其应有的作用。

中国石油集团东方地球物理公司海洋物探处全海燕、徐朝红、杜海涛、韦秀波、刘昭、丁冠东、刘磊等，采集技术中心王建峰、齐英赫等，为本文方法的研究提供了重要的帮助与指导，在此表示衷心感谢。