多风机风洞动力系统性能优化研究

洛阳中重自动化工程有限责任公司 河南洛阳 471039

在风洞系统中，为了对试验物体进行精确的性能测试，需要得到较高压力和较高速度的风流，该种工况通常需要多台风机同步工作，协调运行。为了保证在试验工况及负载变化时风流系统的稳定性，在不改变风机叶轮机械结构和角度的前提下，需要利用风机传动系统动态调整电动机转速，从而实现风速和风量的平滑连续调节，保证调节时风流系统动态及稳态精度[1]。笔者从风洞风机传动系统入手，通过在变频风机传动系统控制器中引入 3 种控制软件，采用合理的速度调节算法，有效解决了功率平衡及转速同步问题，改善了系统低速及高速性能，提高了系统的动静态稳定控制精度。

1 需求分析

对于传统的交流电动机变频调速控制系统，如果负载对控制器的调速性能没有严格的要求，采用常规的 V/F 转速调节控制方式即可实现电动机全功率段的速度调节。对于多台交流电动机拖动的风洞风流系统，由于负载和试验对象对风流系统变化较为敏感，系统因外部扰动，导致风流系统姿态发生变化时，要求调速系统控制器能够采取措施控制风机转速输出，调整风流迅速恢复至稳定状态。此外，对控制器在稳速控制精度，多机同步精度，动态控制精度，负载变化引起转速恢复时间上要求也更加严格。

2 技术应用

为解决上述问题，在传动系统控制器中，引入了3 种控制算法，根据系统工况需求，调节和整定控制器参数，最终达到风流系统所需的要求。

2.1 矢量控制

相较于传统压频比控制算法，采用基于转子磁场定向的矢量控制算法，可实现转矩电流与励磁电流的完全解耦[2]，从而实现转矩电流与励磁电流的精准控制。基于矢量控制算法建立的磁链观测模型如图 1所示。外环为磁链环和转速环，速度环调节输出转矩电流给定信号isT*，磁链环输出励磁电流给定信号isM*。反馈电流经过旋转坐标变换分解为转矩电流分量isT和励磁电流分量isM。isT*、isT经过 PI 调节输出转矩电压分量usT；isM*、isM经过 PI 调节输出励磁电压分量usM。usT、usM经坐标变换后输出三相电压调制波，调制波经 SPWM 模块调制后输出 PWM 开关信号，开关信号驱动 IGBT 产生所需要的电压波形。

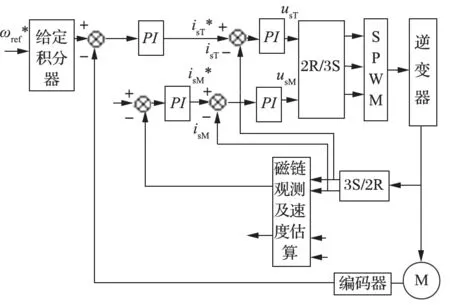
图1 矢量控制逻辑Fig.1 Vector control logic

由图 1 可以看出，如果低速时采用电流磁链模型，高速时采用电压磁链模型，并利用编码器监测的实时转速无扰切换 2 种模型，利用磁链观测器的精确监测数据，进行磁链闭环控制，可以实现对磁链的实时、精确控制，保持磁链稳定，从而减小转矩波动，更好地稳定转速。利用此控制算法，可以保证风机系统在稳态时的速度控制精度和运行时的同步精度。

2.2 微分先行控制

在系统试验工况及负载动态变化时，为了不影响测试效果，需要风机能够抑制风流系统的扰动或快速调节至稳定状态。如果采用常规的 PID 调节控制算法，系统抗扰动能力和恢复时间均不能满足要求。常规 PID 控制算法下系统的阶跃响应及斜坡加速的仿真波形如图 2 所示。

图2 常规 PID 控制算法下的仿真波形Fig.2 Simulation waveform based on conventional PID control algorithm

考虑在保留常规交流电动机调速控制器电流内环、转速外环双闭环控制方式和控制功能的基础上，在控制器的速度闭环反馈路径上增加微分先行，并设置该功能可根据工况自动投切[3]。微分先行是指只对测量值起微分作用的控制算法，微分环节在反馈通道中，位于设定值与测量值比较点之间。增加该功能后的调速控制器结构如图 3 所示。

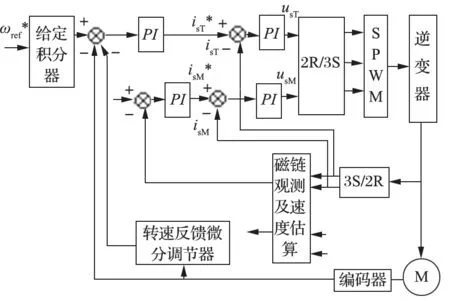
图3 微分先行矢量控制逻辑Fig.3 Differential forward vector control logic

带转速反馈微分先行的系统的阶跃响应、斜坡加速的仿真波形如图 4 所示。与图 2 相比，带转速反馈微分先行系统控制稳定性明显提高，同时消除了系统超调[4]。

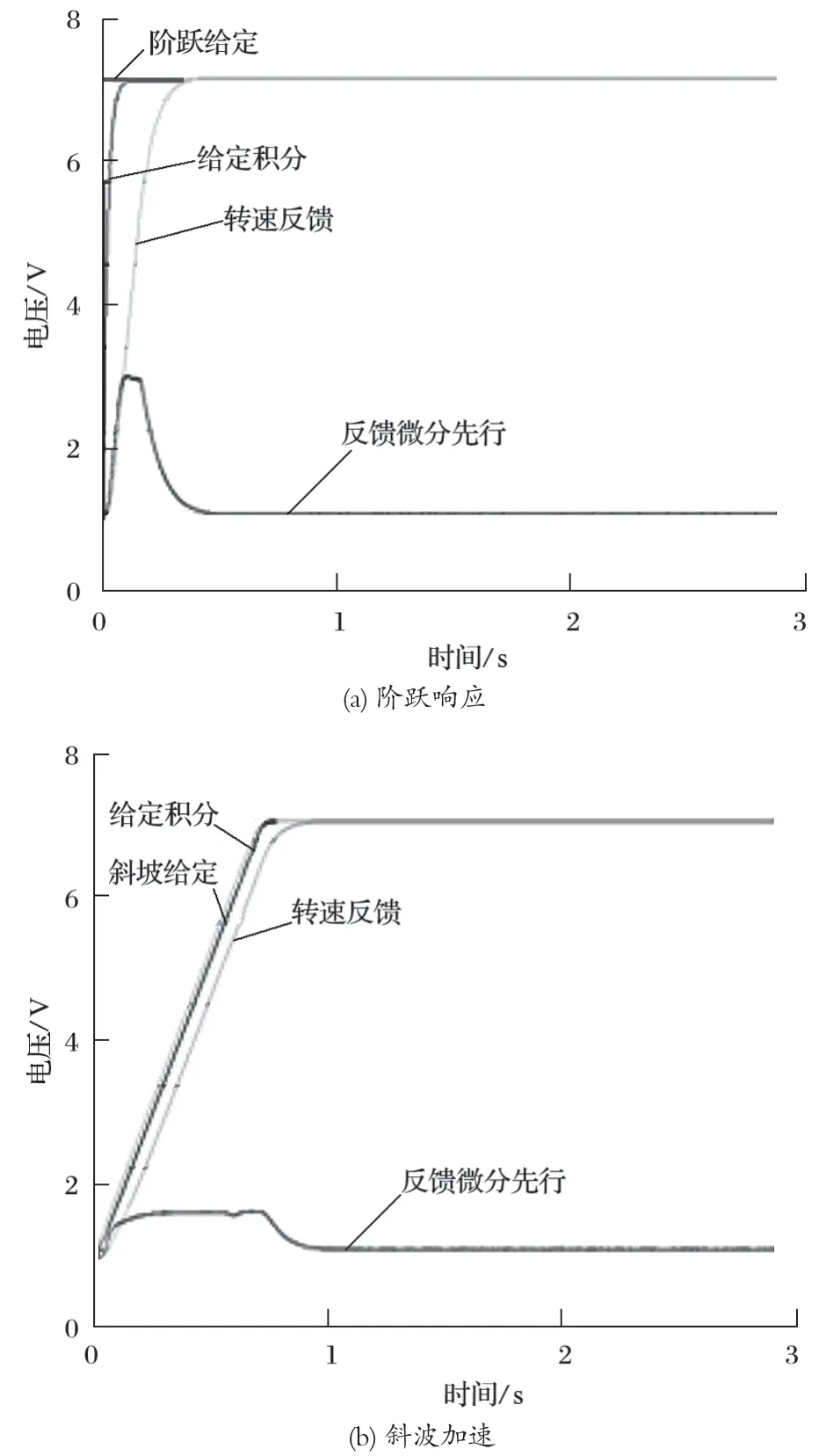
图4 增加微分先行的仿真波形Fig.4 Simulation waveform after adding differential forward

PI 调节器的变对象阶跃响应实测曲线如图 5 所示。由图 5 可以看出，相对于普通 PI 调节器 (5＜Tm＜20)，反馈微分先行的 PI 调节器在控制对象 (5＜Tm＜45) 的适应性上存在明显优势。采用微分先行控制算法，可有效抑制调速系统超调，系统抗扰动能力增强，对于由于负载扰动而导致的风流系统姿态变化，能够快速响应、调节至稳定状态。

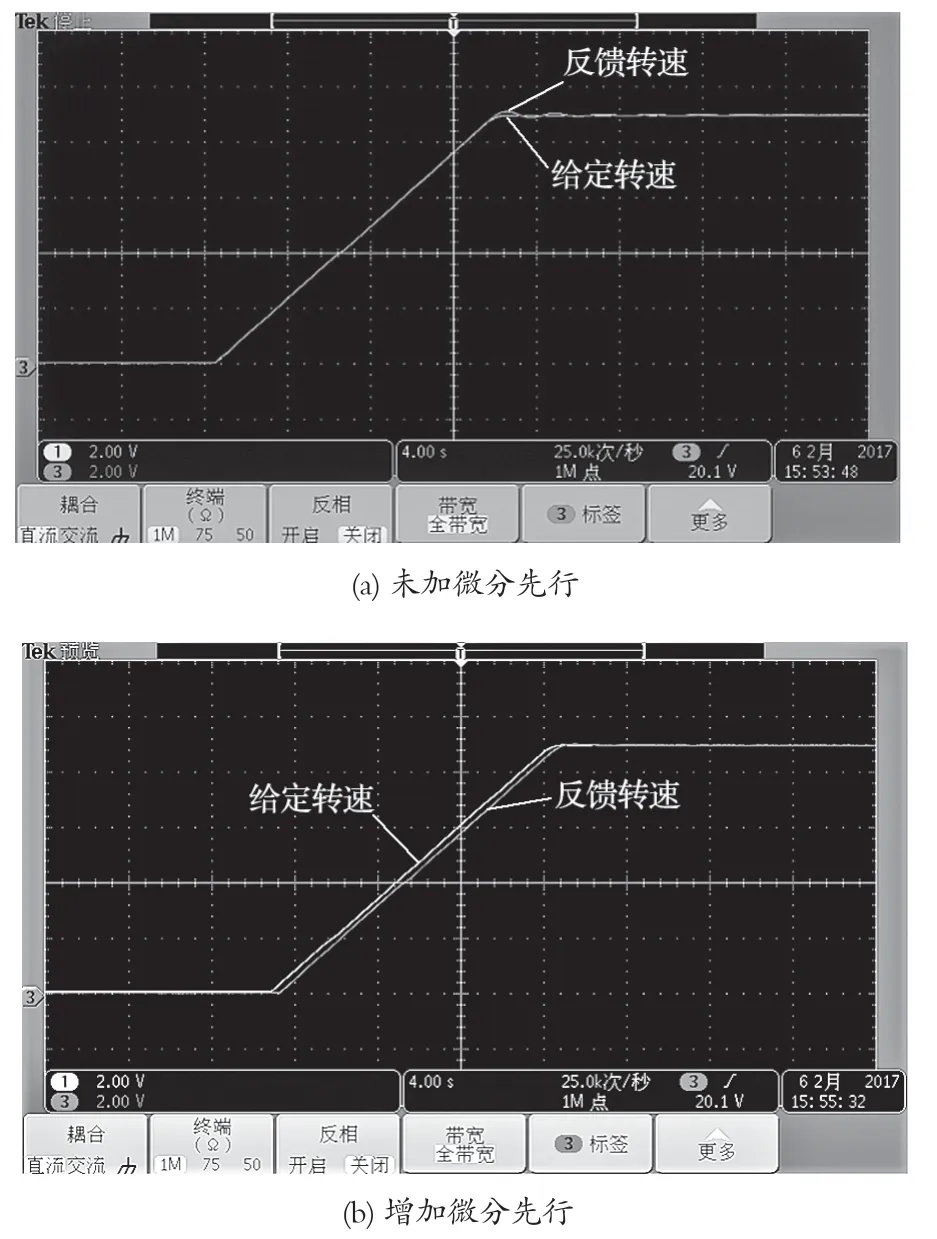
图5 斜波加速实测波形Fig.5 Actual measured waveform of oblique wave acceleration

2.3 变 M/T 的编码器速度计算

在有速度传感器的矢量控制系统中，调速控制器的转速反馈信号由脉冲编码器产生，编码器速度测量的精度直接关系到速度闭环调节的准确性。为了保证电动机在系统要求的额定调速范围内实现电动机转速的精确测量，除了提高编码器转速的计算时钟频率外，还需要采用合适的编码器测量速度计算方法，才能最终保证在高速或低速范围内精确的转速测量[5]。

传统 M 法测速是通过检测一段规定时间间隔内的编码器脉冲个数来计算转速。这种方法高速时时间间隔T内脉冲数M1较多，测速精度较高；低速时规定时间间隔T内脉冲数M1较少，计算误差变大。如果时间间隔T过长，会造成转速响应时间较长，最终影响转速动态响应性能。

传统 T 法测速是通过测量 2 个相邻编码器脉冲时间间隔进行转速计算。这种方法在低速时由于编码器脉冲周期T较长，测速高频时钟M2较多，从而测速精度较高。但在高速时由于编码器脉冲周期T很短，测速高频时钟个数M2较少，测速精度较低。假定电动机额定转速为 500 r/min，编码器测速高频时钟为 40 MHz。采用 T 法进行电动机转速的测量，如果编码器的脉冲数为 2 048，4 倍频后为 8 192，在额定转速下编码器脉冲周期T=14.648 437 5 s，测速高频时钟周期个数M2约为 586 个，测速相对误差为一个测速高频时钟周期内的 1/M2，则测速精度约为0.1706%，稳速精度不高。

通过对 M 法和 T 法测速的各自特点研究发现，如果在低速段和高速段分别采用 T 法和 M 法测速，则可同时兼顾低速和高速的测速精度，并具有良好的实用性。因此在控制器中引入变 M/T 法测速算法，具体实现过程如下：同时对编码器脉冲M1、高频脉冲M2及预设时间T进行定时和计数，设定时间T始终等于编码器脉冲M1的周期和，根据上一次所测转速及时调整预设的编码器脉冲M1的数值，达到实时调整预设时间T的目的[6]。采用变 M/T 法测速后，电动机在全调速区间内，能够实现速度的精确测量，无论在低速段还是高速段，转速测量精度均能达到系统要求，从而保证速度闭环控制。

3 试验验证

采用上述控制算法和控制策略优化后的风机风流系统，经过厂内试验验证，性能及技术指标相较于传统的控制器有很大的提升。通过试验验证、示波器测量，优化后的系统技术参数如表 1 所列。

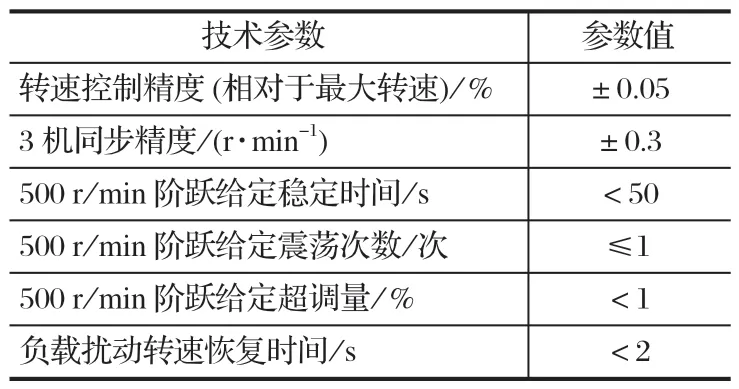
表1 系统技术参数Tab.1 Technical indexes of system

4 结语

为了满足多台风机系统负载的特殊运行要求，在传动系统控制器内加入特殊的控制策略和控制算法。经过试验发现，系统无论在控制精度、低速及高速的静态稳定性和动态及稳态切换过程中的调节快速性等方面都有很大的提升。在实际应用中，可从技术指标

入手，通过监测实际数值进行系统性能验证。