动车组产品可靠性评估与验证

王华胜，朱庆龙，钱小磊，李 昊，蔡 两

（1.中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081；2.北京纵横机电科技有限公司，北京 100094）

随着我国高铁事业的迅猛发展，动车组配属数量快速增长，检修的效率、效益问题变得愈加突出。为实现铁路高质量持续健康发展和提质降本增效的总体目标，以确保质量安全、优化检修标准、降低检修成本、提高检修效率为核心的动车组修程修制改革工作已全面启动，动车组整车及重要部件检修优化试验验证工作正有序开展，如何运用可靠性理论更加科学、高效地开展试验验证工作成为目前迫切需要研究的课题。

在航空、航天、军工等领域，针对特定产品可靠性评估与验证开展了大量工作，提出并建立一些适用而有效的理论和方法［1-3］。如：火炮可靠性试验技术、军用雷达可靠性试验方法等。动车组作为大型高新技术装备，不仅结构功能复杂，而且整车和零部件等动车组产品的可靠性要求各异，如何在资源有限的条件下高效获得动车组产品的可靠性评估和验证结果尚未见到相关文献介绍。

本文旨在针对我国动车组运用维修管理特点和修程修制改革试验验证实际需求，依据可靠性试验验证理论，研究动车组产品可靠性评估与验证方法，实现动车组产品可靠性既有水平的定量评估和潜在能力的挖掘验证，为当前动车组修程修制改革试验验证工作提供科学技术支撑。

1 动车组产品可靠性评估方法

我国动车组在长期运营实践中积累了大量运用检修数据，涵盖不同车型产品、不同运用条件、不同寿命周期阶段的可靠性信息，具有样本量大、数据真实、服役条件复杂等特点，特别是在大样本数据中包含一些关键部件的极小概率故障信息，为动车组安全性、可靠性评估提供了强大的数据支撑。

1.1 分类评估原则

产品可靠性受多方面因素影响，使用条件不同、产品类型不同，可靠性均有所不同；此外，产品功能重要程度不同，相应的可靠性水平和要求也会有较大差异。为此，应针对动车组产品特点，按照一定的原则分级、分类开展可靠性评估，才能获得更加客观、准确的评估结果。

（1）按照不同车型分类评估。我国动车组型号、种类多，如：有CRH1A，CRH2A，CRH5A，CRH3C，CRH380A，CRH380B，CRH380D，CR400AF/BF 等典型车型［4］，在运行速度、技术特点、故障规律等方面均有较大差异，应分别进行可靠性评估。

（2）按照不同产品分类评估。动车组由车体、转向架、制动、牵引、辅助、网络等主要功能系统构成［5-6］，每个系统又包含诸多层级的产品，不同产品的可靠性规律特点不同，需要分类评估；即使同一产品，由于生产厂家或批次不同，差异也会较大，评估时可能需要进一步分类；新品与修复品在服役性能、剩余寿命、故障规律等方面均有显著差别，也应分类进行可靠性评估。

（3）按照不同运用条件分类评估。我国幅员辽阔、运用环境条件复杂，动车组运营方式、交路多样，如：运行线路包括无砟线路、有砟线路；运营方式分为长交路干线运输、短途城际运输；地域环境主要包括高原、高寒、高温、高湿、多风沙等。不同运用条件对动车组可靠性影响不同，应分类评估。

（4）按照不同故障后果分类评估。不同功能产品的故障后果严重程度会有很大差异，如：牵引电机轴承与换气风机轴承虽同为滚动轴承，但故障影响却有天壤之别。文献［7-8］按照故障严重程度不同，将动车组故障分为A 类故障、B 类故障、C类故障、D 类故障，并提出不同的可靠性指标要求。

（5）按照不同置信度要求分类评估。置信度可反映产品可靠性评估结果的可信程度，对于高安全、高可靠的关键产品，通常要在较高置信度下进行可靠性评估。为此，建议针对动车组产品安全相关程度不同分别设置置信度要求：①可能导致事故或安全隐患的关键产品置信度可取99%，包括车轴、车轮、轴箱轴承、齿轮箱等；②可能导致A类、B 类故障或严重影响行车的重要产品置信度可取95%，包括安全监测装置、制动重要控制部件、安全环路部件等；③可能导致C类故障或运行品质降低的重点产品置信度可取90%，如：车体侧门、牵引系统部件、网络控制部件；④故障后果不严重的其他产品置信度可取50%，或进行统计平均意义上的点估计。

1.2 故障概率置信评估

可靠度与故障概率从正反2 个方面反映了产品的质量水平，二者在概念上既对立、又统一。设某成败型产品的故障概率为F，则n个产品进行试验恰好故障i次的概率Pi可用二项分布描述为

进一步地，n个产品在试验中故障次数不超过r次时的累计概率α为

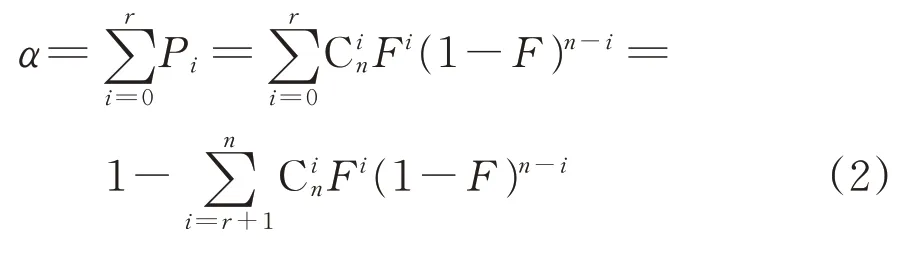
由式（2）可知，产品故障概率F较大时，n个产品在试验中会倾向发生较多次故障，不超过r次故障的累计概率α较小，或者说故障发生次数落在r+1～n范围内的概率1-α较大；反之，F较小时，n个产品在试验中会倾向发生较少次故障，不超过r次故障的累计概率α较大，或者说故障发生次数落在r+1～n范围内的概率1-α较小。产品验收时，若规定故障次数不超过r次就予以接受，则该产品被接受的概率为α，被拒收的概率为1-α。

产品的故障概率与验收时的接受概率间的基本关系如图1 所示。由图1 可以看出：当F＞FUL时，接受概率值范围为0～α；当F＜FUL时，接受概率值范围为α～1.0。故FUL可视为α置信度下故障概率F的置信下限FL，同时也可视为1-α置信度下的故障概率置信上限FU。

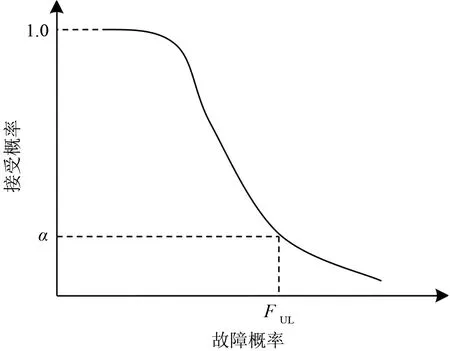
图1 产品故障概率与验收接受概率关系

1.3 可靠度置信下限评估

在实际评估中常常会遇到在不同样本量下计算得到的可靠度点估计结果相同，但结果可信程度却不相同的情况，显然大样本下获得的评估结果更加可信。为此，人们引入了可靠性置信评估的概念。工程实际主要从产品更加安全、可靠角度考虑，通常希望获得α置信度下产品的可靠度置信下限RL。由于存在RL=1-FU，故式（2）变为

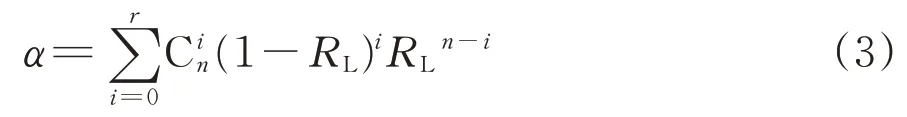
利用二项分布与F分布间变换关系［9-10］，可得到1-α置信度下可靠度置信下限RL为

上式表明，若n个产品进行试验出现r次故障，则由式（4）可得到置信度为1-α下的可靠度置信下限RL。

若能获得上述r次故障发生时的具体时间或里程，则可以得到各故障时间点对应的可靠度置信下限，进而给出该产品使用期内可靠度置信下限曲线，定量呈现其服役期内可靠性变化情况。

1.4 故障率置信上限评估

按照产品故障模式和机理不同，故障概率函数F（t）可表现为不同的分布函数类型，常见的故障概率分布函数包括指数分布、正态分布、对数正态分布、威布尔分布等。其中指数分布函数形式简单、应用范围广，理论和实践均证明在正常运用维护条件下，运用质量稳定的动车组等大型复杂机电装备故障规律近似服从指数分布［11-14］；此外，经过早期故障筛选的电气产品故障规律也近似服从指数分布。

指数分布函数的一般形式为

式中：λ为故障率。

当故障率λ不大时，存在以下近似关系。

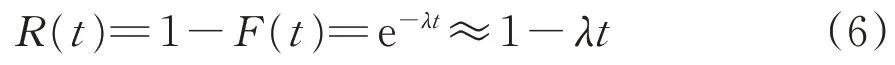
式中：R(t)为可靠度。

将式（6）代入式（3）得到

再利用二项分布与泊松分布的关系，式（7）可进一步变换为

式中：T为产品累计试验时间。

为便于计算，利用分布函数间的关系［15］，可将式（8）变换为

式中：为自由度为2（r+1）时χ2分布的上侧分位数。

式（9）表示：故障规律近似服从指数分布的产品，若在累计试验时间T内的故障发生次数不大于r，则可认为1-α置信度下该产品的故障率不大于λ。

基于我国动车组产品可靠性实际状况，整车百万km 故障率可初步划分为0.1，0.2，…，1.0 次共10个等级，表1示例给出动车组在一定累计运行里程内故障发生次数分别为0～30 次时，对应的95%置信度下动车组百万km 故障率置信上限评估等级。由表1 可知：如某型动车组在累计运行120百万km 期间发生A 类故障不超过15 次，则95%置信度下该动车组百万km 故障率置信上限评估结果为0.2次。

2 动车组产品可靠性验证方法

按照当前我国动车组修程修制改革要求，需要对整车及重要部件检修周期延长后的可靠性状况进行试验验证，为维修优化的可行性提供技术支撑。

2.1 验证优化原则

为了更加快速、高效、经济地获得可信的试验验证结果，建议在制定动车组试验验证方案时考虑以下原则。

（1）最少验证样本。试验样本量越大，投入的试验时间、工时、费用等资源越多，验证成本越高。验证同样的可靠性水平，试验方案中允许的故障数越多，需要投入的试验样本量越大，试验时间也越长；相反，允许的故障数越少，需要投入的试验样本量越小，试验时间也越短。因此，为减少试验样本和时间，建议优先按照零故障原则确定试验方案。

（2）最短验证时间。为了在最短时间内获得可靠性验证结果，可以充分借用相同或相近产品试验数据和结果，或者借用更苛刻条件下的试验结果或数据作为补充信息进行评估，减少常规试验样本和试验时间。

（3）最低验证成本。鉴于动车组产品功能重要程度不同，相应的可靠性验证目标值应分级设定，分阶段、分项目逐级开展验证工作，精准投入试验验证资源。如：首先选取小批量动车组产品进行试验验证，完成大部分产品一般置信度下的可靠性验证；其次小批量产品验证通过后启动中等批量产品试验验证，并对一些重要产品进行较高置信度下可靠性追加验证；最后开展大批量试验验证，对涉及安全的少数关键产品实施更高置信度下的可靠性进一步追加验证。

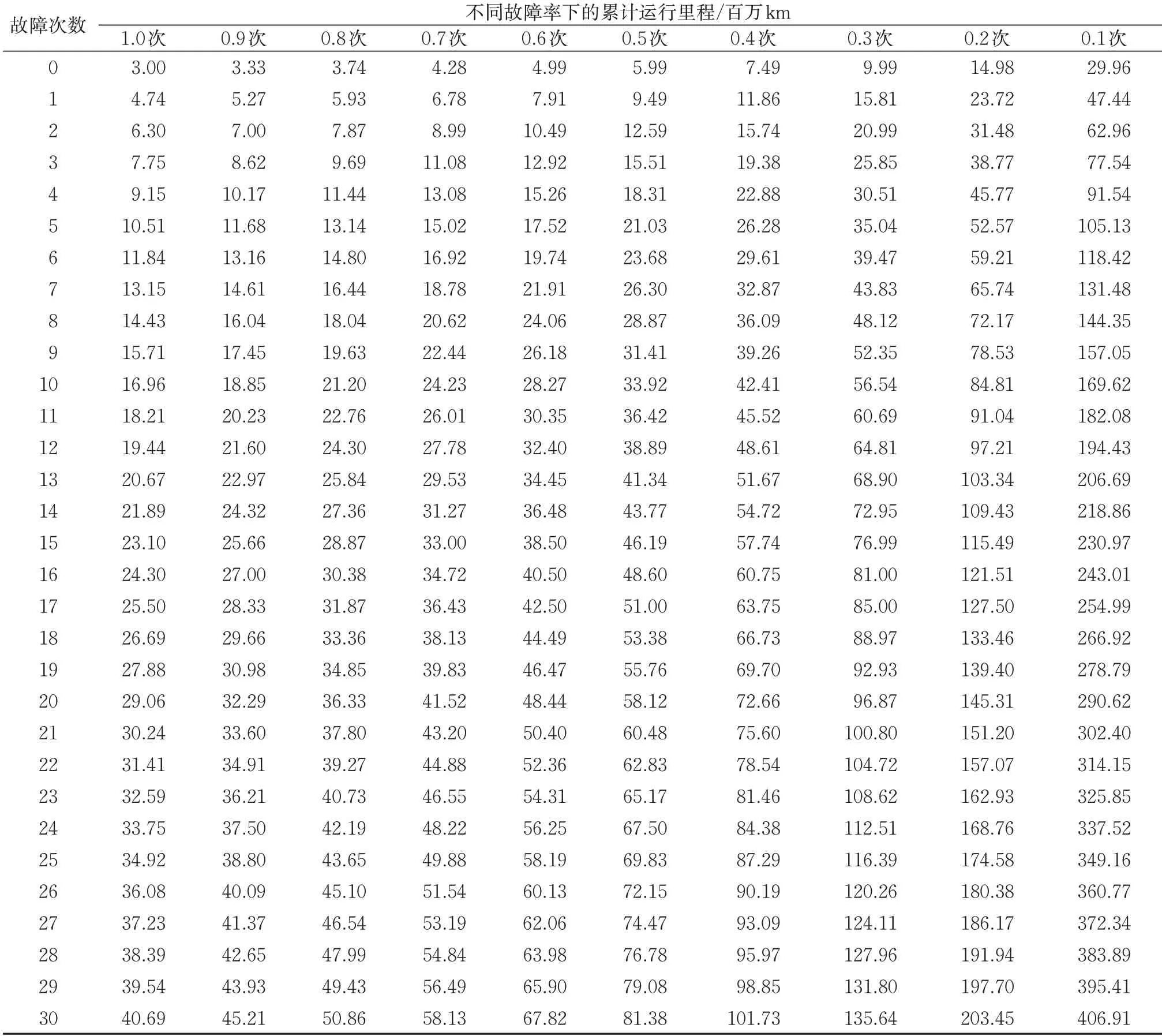
表1 动车组累计运行里程内故障次数与故障率置信上限对应表

2.2 可靠度验证方法

由于产品验证样本量与置信度、可靠度置信下限和故障次数间存在式（3）关系，在给定的置信度和可靠度置信下限要求下，允许的故障次数越少则要求投入试验的样本量相应也越少。按照最小样本试验验证原则，在式（3）中令故障数r=0，即n个产品试验均无故障，则试验样本量n、置信度1-α与可靠度置信下限RL间存在如下关系。

进一步整理得到

针对我国动车组产品可靠性实际水平和验证需求，依据式（11）分别计算给出在无故障状况下，置信度分别为50%，90%，95%，99%及可靠度置信下限分别为0.90～0.99，0.991～0.999 时需要的试验验证样本量并进行圆整处理，结果分别见表2 和表3。如：为验证某产品可靠性能否达到95%的可靠度置信下限0.99 水平，参照表2 可知需投入299 个产品进行试验验证，若试验过程中无故障发生，则可认为其可靠性指标通过验证；否则不能通过验证。

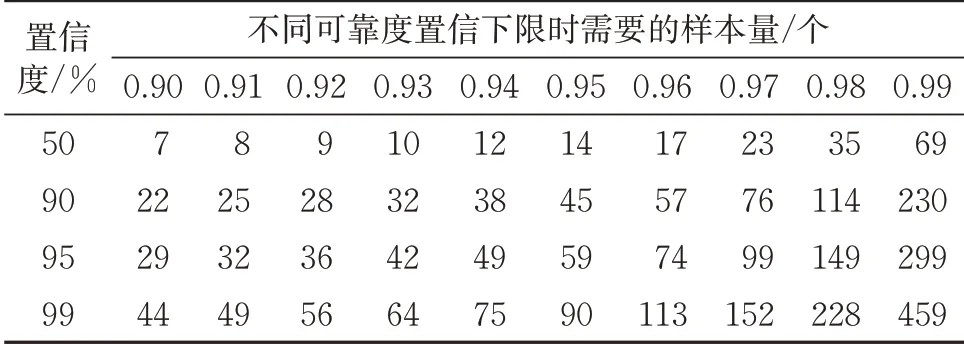
表2 无产品失效时0.90～0.99 可靠度置信下限时需要的样本量

表3 无产品失效时0.991～0.999可靠度置信下限时需要的样本量

2.3 故障率验证方法

对于故障规律近似服从指数分布的动车组产品，可以针对故障率参数开展可靠性验证。同理，为提高验证效率、缩短验证时间，可优先按照零故障准则确定验证方案，即在式（9）中令r=0 计算产品累计试验时间。

针对我国动车组产品故障率实际水平及验证需求，得到无故障状况下、置信度分别为50%，90%，95%，99%及百万km 故障率上限分别为0.1～1.0 次时需要的产品累计试验时间即运行里程。如：为验证某型动车组95%置信度下百万公里A 类故障率上限不高于0.1 次，参照表4 可知该型动车组需在无A 类故障发生情况下累计运行里程不少于29.96百万km。

表4 动车组产品无失效时故障率置信上限验证里程

3 示例分析

3.1 整车故障率评估与验证

某型动车组批量投入运用后累计运行约210 百万km，期间累计发生A 类故障29 件，参照表1 进行故障率评估，可以得到该型动车组百万km（A类）故障率95%置信上限不大于0.2次。

现拟在百万公里A 类故障率指标不降低的前提下，对该型动车组开展三级修周期上限由132 万km 延长至165 万km 的可行性试验验证。按照无A类故障发生原则制定试验验证方案，则由表3 可知，在95%置信度下百万km 故障率不高于0.2 次的累计运行里程应不低于14.98 百万km，则至少需选取46 列该型动车组完成由132 万km 运行至165 万km、累计运行15.18 百万km 的检修周期延长验证试验。若试验期间动车组无A 类故障发生，则可认为：该型动车组三级修周期上限由132 万km 延长至165 万km 后的百万km（A 类）故障率仍可保持在0.2次水平，检修周期延长基本可行。

3.2 部件可靠度评估与验证

某型动车组轴箱轴承装车使用量为32 000 套，运行至分解检修前累计发生运行报警故障24 次，鉴于轴箱轴承属关键部件，需要按照99%的高置信度对其可靠度置信下限进行评估，由式（4）可以计算出该轴承在99%置信度下的可靠度置信下限为0.998 8。

轴箱轴承主要结合整车三级修进行分解检修，目前动车组整车检修周期间隔上限为132 万km，为适应其延长至165 万km 的需求，需要针对该型动车组整车检修周期间隔延长后的轴箱轴承可靠性进行试验验证。硬件产品可靠度通常会随使用时间的增加而下降，轴箱轴承作为高安全部件，其分解检修周期间隔上限由132 万km 延长至165 万km 后可靠度可能会有小幅下降，结合实际运用情况，可合理假定其可靠度置信下限由上述0.998 8 小幅下降至0.998 6。按照无故障原则制定最小样本量试验验证方案，由式（11）计算得到该轴箱轴承的无故障状况下的最小试验样本量约为3 245 套，每列动车组配64 套，则大约需要50.7 标准组动车组。初步验证方案为：选取51 标准组配置该轴箱轴承的动车组完成165 万km 试验考核，期间若无故障发生，则说明该轴承检修周期间隔延长后的可靠性水平仍能维持99%置信度下可靠度置信下限不低于0.998 6。

4 结论及建议

（1）针对动车组不同产品类别、运用条件、故障级别，按照不同置信度要求分级、分类进行可靠性评估，使评估结果更加客观、准确。

（2）给出动车组产品可靠度置信下限估计公式；针对故障规律服从指数分布产品，给出故障率置信上限评估方法；基于动车组可靠性实际状况，给出95%置信度下，动车组一定累计运行里程内故障发生数与故障率置信上限评估表。

（3）从最小样本、最短时间、最低成本等角度，提出动车组可靠性试验验证方案优化原则，在获得可信验证结果的同时，使验证工作更加高效、经济。

（4）按照无故障原则给出动车组可靠度置信下限验证方法，示例给出特定置信度下、无故障时常用可靠度置信下限验证样本量方案表；针对故障规律服从指数分布情形，按照无故障原则给出故障率置信上限验证方法，示例给出特定置信度下、无故障时常用故障率置信上限验证里程方案表。

（5）动车组可靠性评估与验证方法尚需不断探索，建议在实践中对验证方案、方法、标准等进一步优化和完善，以便为我国动车组修程修制改革试验验证工作提供科学技术支撑。