p值法在岩体初始地应力场反演中的应用

蒙 伟，何 川，晏启祥，郭德平，李瑞林，唐进才，廖烟开，陈子全

（1.西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031；3.四川省铁路产业投资集团有限责任公司 叙镇铁路有限责任公司，四川 成都 610000）

近年来，随着西部大开发战略的逐步深入实施，中国西部区域涌现出大量“长洞线、大规模、深埋深”隧道等地下工程［1-5］。该区域存在的挤压构造运动［6］，导致岩体初始地应力场的分布规律极其复杂，且岩体竖向初始地应力常小于水平初始地应力［7］，即该区域因印度洋板块和亚欧板块的碰撞挤压存在水平构造应力。因此，对于该区域的长、大及深埋隧道等地下工程，研究岩体的初始地应力场具有重要的实际意义［8］。岩体的初始地应力可采用应力解除法、水压致裂法等方法在现场测试得到，但受测试费用和钻孔条件等限制而不能大范围地应用，且测试得到的初始地应力仅能反映局部区域的初始地应力场变化规律，无法表达岩体宏观分布的初始地应力场，故为得到隧道等地下工程岩体宏观分布的初始地应力场，基于现场实测应力数据，反演隧道等地下工程岩体的初始地应力场，具有重要的理论意义。

在岩体初始地应力场多元线性回归反演中，郭怀志等［9］提出了基于最小二乘法的地应力场反演分析方法，因该分析方法的解唯一，被广泛采用至今。张建国等［10］、张延新等［11］、张勇慧等［12］、裴启涛等［13］、汪 波 等［14］、张传庆等［8］、王金安等［15］、张强勇等［16］、张社荣等［17-18］、代聪等［19］、颜天佑等［20］、蒙伟等［21-22］，周子寒等［23］、张涛等［24］、余大军等［25］均采用此分析方法反演了岩体的初始地应力场。在多元线性回归反演过程中，回归模型和回归系数的显著性检验是必不可少的步骤，而上述研究在进行显著性检验时，对岩体初始地应力场回归模型一般采用F检验进行显著性检验，对回归系数一般采用t检验进行显著性检验。F检验和t检验均存在1 个缺点：仅能给出判断显著性的依据，无法给出依据的强度，从而导致回归模型的可靠性得不到充分地验证。

p值法检验是利用p值来确定是否拒绝原假设的方法［26］，不仅能够给出判断显著性的依据，而且能给出依据的强度，因此能够更充分地验证所采用回归模型的可靠性。此外，p值法检验直接以p值与显著性水平α比较判断是否满足显著性检验，不需要与在给定显著性水平α下的临界值进行比较，故p值法检验可更加直观方便地判断回归模型和回归系数是否满足显著性检验。基于此，分别将回归模型的p值法检验与F检验、回归系数的p值法检验与t检验进行理论分析，提出在岩体初始地应力场反演过程中采用p值法进行显著性检验的方法；并以新建叙永至毕节铁路（川滇段）的斑竹林隧道工程为例，验证该方法的合理性和有效性。

1 显著性检验方法

对岩体初始地应力场反演时，首先假定岩体初始地应力场回归模型的型式，但模型中参数未知；然后提出k个子应力场与岩体初始地应力场存在线性相关的假设（回归模型的假设），再提出k个子应力场对岩体初始地应力场的影响都显著的假设（回归系数的假设）；最后依据样本，采用p值法检验，或者F检验和t检验检验假设的显著性，根据其显著性做出是接受还是拒绝的决策。

1.1 回归模型的显著性检验

1.1.1F检验

假定反演岩体初始地应力场的线性回归模型为

式中：σjq为实测的第q个测点第j个应力分量的岩体初始地应力；为计算的第q个测点第j个应力分量第i个自变量的岩体初始地应力；k为自变量个数；Ci为第i个自变量的回归系数。

基于概率论与数理统计理论及假设检验原理，回归模型的F检验过程如下。

原假设H0：C1=C2=…=Ck=0。原假设H0为待检验的有关总体分布的1项命题的假设。其拒绝域为

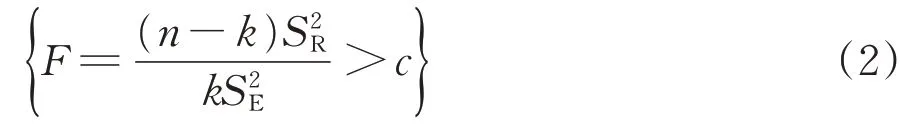
其中，

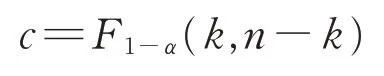
式中：F为检验统计量的样本观测值；n为样本个数；为回归平方和；为残差平方和；c为回归模型的F检验在显著性水平α下的临界值；F1-α为在显著性水平α下的F检验。

1.1.2 与F检验对应的回归模型p值法检验

在岩体初始地应力场多元线性回归反演过程中，与F检验对应的回归模型p值法检验过程如下［26］。

原假设H0：C1=C2=…=Ck=0。其拒绝域为

其中，

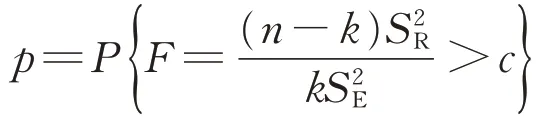
式中：p为由检验统计量的样本观测值得出的原假设可被拒绝的最小显著性水平；P为概率。

当p≤α时，即在显著性水平α下拒绝原假设H0，满足回归模型的显著性检验。

由式（2）和式（3）可知，p值法检验与F检验的回归模型原假设H0相同，故回归模型的p值法检验结果与F检验结果相同，说明可采用p值法检验回归模型的显著性。

在多元线性回归反演中，回归模型显著并不意味着每个自变量对因变量的影响都显著，因此，还需对每个自变量进行显著性检验。

1.2 回归系数的显著性检验

1.2.1t检验

对岩体初始地应力场进行多元线性回归反演时，回归系数的t检验过程如下。

原假设H0：Ci=0i=1，2，…，k。其拒绝域为

其中，

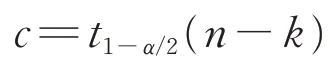
式中：Ti为检验统计量的样本观测值；SE为残差平方和的算术平方根；cii为法方程式系数矩阵的逆矩阵元素。

1.2.2 与t检验对应的回归系数p值法检验

在岩体初始地应力场多元线性回归反演过程中，与t检验对应的回归系数p值法检验过程如下。

原假设H0：Ci=0i=1，2，…，k。其拒绝域为

其中，

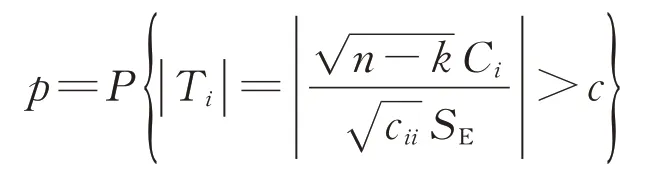
当p≤α时，即在显著性水平α下拒绝原假设H0，满足回归系数的显著性检验。

由式（4）和式（5）可知，p值法检验与t检验的回归系数原假设H0相同，故回归系数的t检验结果与p值法检验结果相同，说明可采用p值法判断回归系数的显著性。

1.3 p值法检验的优点及应用

1.3.1p值法检验的优点

由式（2）和式（4）可知：回归模型的F检验和回归系数的t检验均需要将检验统计量的样本观测值与在给定显著性水平α下的临界值进行比较，才能判断显著性。而目前在现代计算机软件程序中，例如Excel，SPSS，SAS 和Minitab 等软件程序，均未直接给出此临界值，即还需要查表才能获得此临界值，故不便于直观判断是否通过显著性检验；而在p值法检验中，直接以p值与显著性水平α比较判断是否通过显著性检验，不需要与在给定显著性水平α下的临界值进行比较，故p值法检验较F检验、t检验可更加直观方便地判断回归模型和回归系数是否满足显著性检验。因此，在岩体初始地应力场反演过程中，建议采用p值法检验判断回归模型和回归系数的显著性。

综上所述，p值法检验可更加直观方便地判断回归模型和回归系数是否满足显著性检验，并且能给出依据的强度。因此，在岩体初始地应力场反演过程中，建议采用p值法判断回归模型和回归系数的显著性和可靠性。

1.3.2p值法检验的应用

p值表示反对原假设依据的强度，p值越小，则反对原假设的依据越强。根据统计学家给出的“不同p值大小对应拒绝原假设的不同依据规律”［26］可得：若回归模型和回归系数检验对应的p值分别为p≤0.01、0.01＜p≤0.05、0.05＜p≤0.1、p＞0.1，则以所采用的回归模型反演岩体初始地应力场的依据分别为很强、强、弱、无。若依据是弱的或者没有依据的，则需改变模型的型式或者改变边界荷载的分布形式。即通过p值可更充分地验证所采用回归模型的显著性和可靠性。

回归模型的F检验和p值法检验、回归系数的t检验和p值法检验对比见表1。

表1 回归模型和回归系数的显著性检验

2 初始地应力场多元线性回归反演实例

2.1 工程概况

新建叙永至毕节铁路（川滇段）位于川滇黔三省交界的边远山区，其中全线控制工期工程为斑竹林隧道，斑竹林隧道全长12 758 m，最大埋深约570 m，其隧址区属低中山侵蚀地貌，地形连绵起伏，隧址区海拔约1 000～1 730 m。为了解斑竹林隧址区初始地应力状态，在里程DK226+157 附近，进行水压致裂试验，钻孔编号为DZ-BZLS深-01，钻孔所钻取的岩芯为页岩、白云岩夹泥岩、白云岩，其物理参数见表2，测得的初始地应力见表3。

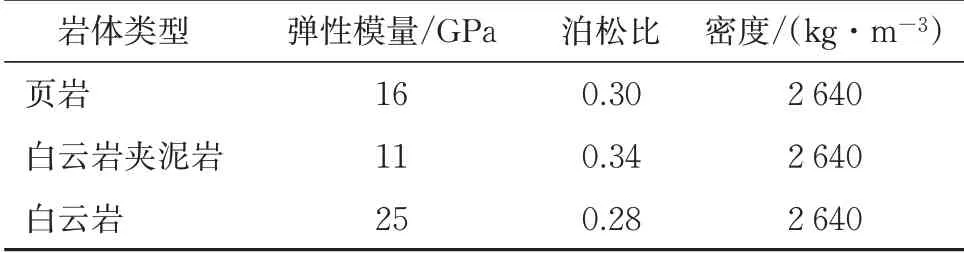
表2 物理参数

表3 实测岩体初始地应力

由表3 可知，最小水平主应力大于垂直应力，表明该钻孔附近区域存在强烈的构造运动，故有必要反演该钻孔附近区域的岩体初始地应力场。

2.2 建立岩体的三维数值模型

岩体的三维数值模型的底面为隧道高程以下300 m，顶面为实际地形，划分网格后的三维数值模型如图1所示，共计单元566 807个，节点101 210个；取隧道轴线方向为x轴的方向。

图1 岩体的三维数值模型（单位：m）

2.3 施加重力和构造荷载

假定该隧址区岩体由自重和挤压构造应力场组成，由于水压致裂测试方法无法测得铅垂面内的剪切应力，故剪切构造荷载仅考虑水平面内的剪切构造荷载。三维数值模型的重力和构造荷载如图2 所示。图中：G为重力荷载；σx为x方向的均布构造荷载；σy为y方向的均布构造荷载；τxy与τyx为xy平面的均布剪切构造荷载。

2.4 岩体初始地应力坐标系转换

三维数值模型采用坐标系xoy，水压致裂实测初始地应力采用坐标系now，如图3 所示。图中：σx为x方向的应力；σy为y方向的应力；τxy与τyx为剪切应力；σh为最小水平主应力；σH为最大水平主应力。由于模型与实测两者间的坐标系不一致，因此，需要将测得的表3中的初始地应力转换为坐标系xoy下的初始地应力，转换公式为

图2 岩体的重力和构造荷载

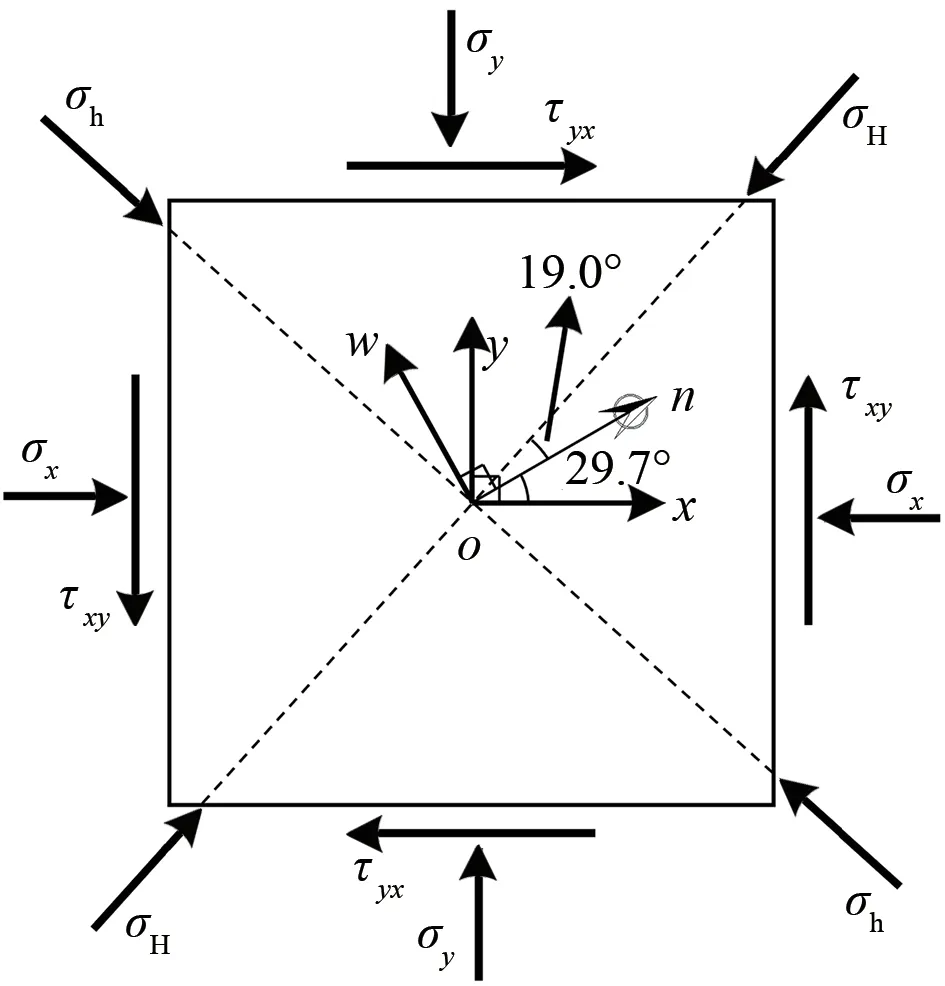
图3 xoy与now坐标系下的初始地应力（序号1）

式中：σij和σi′j′分别为转换前、转换后的初始地应力；αi′i和αj′j分别为转换系数。

2.5 回归反演岩体初始地应力场

在图2 的重力和构造荷载作用下，假定岩体初始地应力场反演的线性回归模型为

式中：为在重力荷载G作用下的应力计算值；为在x方向构造荷载σx作用下的应力计算值；为在y方向构造荷载σy作用下的应力计算值；为在xy平面的均布剪切构造荷载τxy与τyx作用下的应力计算值；C1，C2，C3，C4为相应自变量的回归系数。

通过最小二乘法使应力实测值与计算值的残差平方和最小，即可求出相应自变量的回归系数；同时，对回归模型和回归系数进行显著性检验，以判断采用式（7）的线性回归模型是否显著与可靠。在显著性水平α=0.05 下，通过Excel 软件给出的检验统计量、回归系数、p值分别见表4和表5。

表4 方差分析

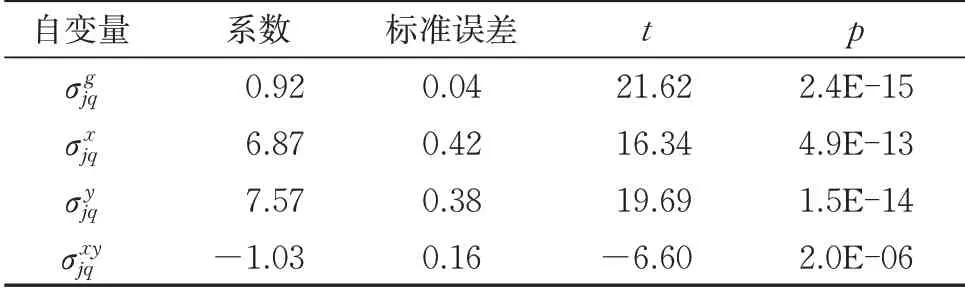
表5 回归系数与p值

2.5.1 回归模型的显著性检验

1）p值法检验

原假设H0：C1=C2=C3=C4=0。

根据表4 中的数据可得，回归模型对应的p=8.0E-20；在显著性水平α=0.05 下，可见p=8.0E-20＜α=0.05。由此可直观地判断出：拒绝原假设H0，满足回归模型的显著性检验。

同时，由于回归模型对应的p=8.0E-20＜0.01，则表示拒绝H0的依据很强，即拒绝C1=C2=C3=C4=0 的依据很强，也就是说，与σjq存在线性关系的依据很强。

2）F检验

原假设H0：C1=C2=C3=C4=0。

拒绝原假设H0表示：拒绝C1=C2=C3=C4=0，即C1，C2，C3，C4不全为0，即在显著性水平α=0.05下，与σjq存在线性关系。但是，存在线性关系的依据强度还无法判断。

2.5.2 回归系数的显著性检验

1）p值法检验

原假设H0：C1=0。

根据表5 中的数据可得，与C1对应的p=2.4E-15，在显著性水平α=0.05 下，可见p=2.4E-15＜α=0.05。由此可直观地判断出：拒绝原假设H0，满足回归系数C1的显著性检验。对于C2，C3，C4，对应的p值分别为4.9E-13、1.5E-14、2.0E-06，均小于0.05，因此，在显著性水平α=0.05 下，均拒绝原假设H0，满足回归系数C2，C3，C4的显著性检验。

同时，由于与C1对应的p=2.4E-15＜0.01，则表示拒绝H0的依据很强，即拒绝C1=0 的依据很强，也就是说与σjq存在线性关系的依据很强。此外，与C2，C3，C4对应的p值均小于0.01，同理，与σjq存在线性关系的依据均很强。

再者，在与C1，C2，C3，C4对应的p值中，与C1对应的p值最小，依据“p值越小，则反对原假设的依据越强”［26］可知：与σjq存在线性关系的依据在图2 的4 个子应力场中是最强的。这是由于在计算图2（a）的自重应力场时，施加的是被认可的重力加速度模拟自重应力场，而在计算图2（b）、2（c）、2（d）的构造应力场时，施加的是均布构造荷载来等效实际岩体中的复杂构造荷载，因此，一般反演得到的自重应力场与岩体初始地应力场存在线性关系的依据是最强的。即通过p值也可验证反演结果的可靠性。

2）t检验

原假设H0：C1=0。

拒绝原假设H0表示：拒绝C1=0，即在显著性水平α=0.05 下，与σjq存在线性关系，但存在线性关系的依据强度还无法判断。

同理，对于C2，C3，C4可得

|T2|=≈16.34＞t1-α/2(n-k)=2.086，|T3|=≈19.69＞t1-α/2(n-k)=2.086，|T4|=≈6.60＞t1-α/2(n-k)=2.086。即在显著性水平α=0.05 下，均拒绝原假设H0，满足回归系数C2，C3，C4的显著性检验。

综上所述，回归模型和所有回归系数对应的p值都小于0.01。因此，采用式（7）的线性回归模型反演斑竹林隧址区岩体初始地应力场的依据很强。可见，通过p值可更充分地验证所采用回归模型的可靠性。则将表5 中的回归系数代入式（7），可得该区域的岩体初始地应力场为

2.6 反演结果对比

依据式（8）可计算得到三维数值模型中任意1 点的应力。为了验证反演结果，将应力计算值与应力实测值进行对比分析。针对表3 中的6 个测点，采用式（8）可计算得到应力计算值，采用式（6）进行坐标转换可得到应力实测值；应力实测值与应力计算值的差值作为残差值。2 组数据均列表见表6。同时绘制应力计算值和应力实测值随埋深的变化曲线如图4所示。

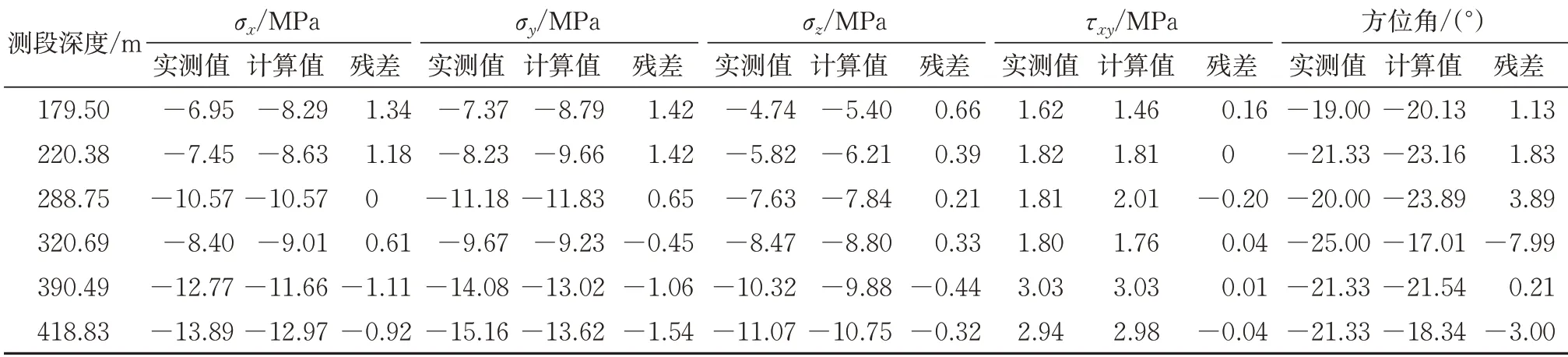
表6 应力及方位角的计算值、实测值及残差

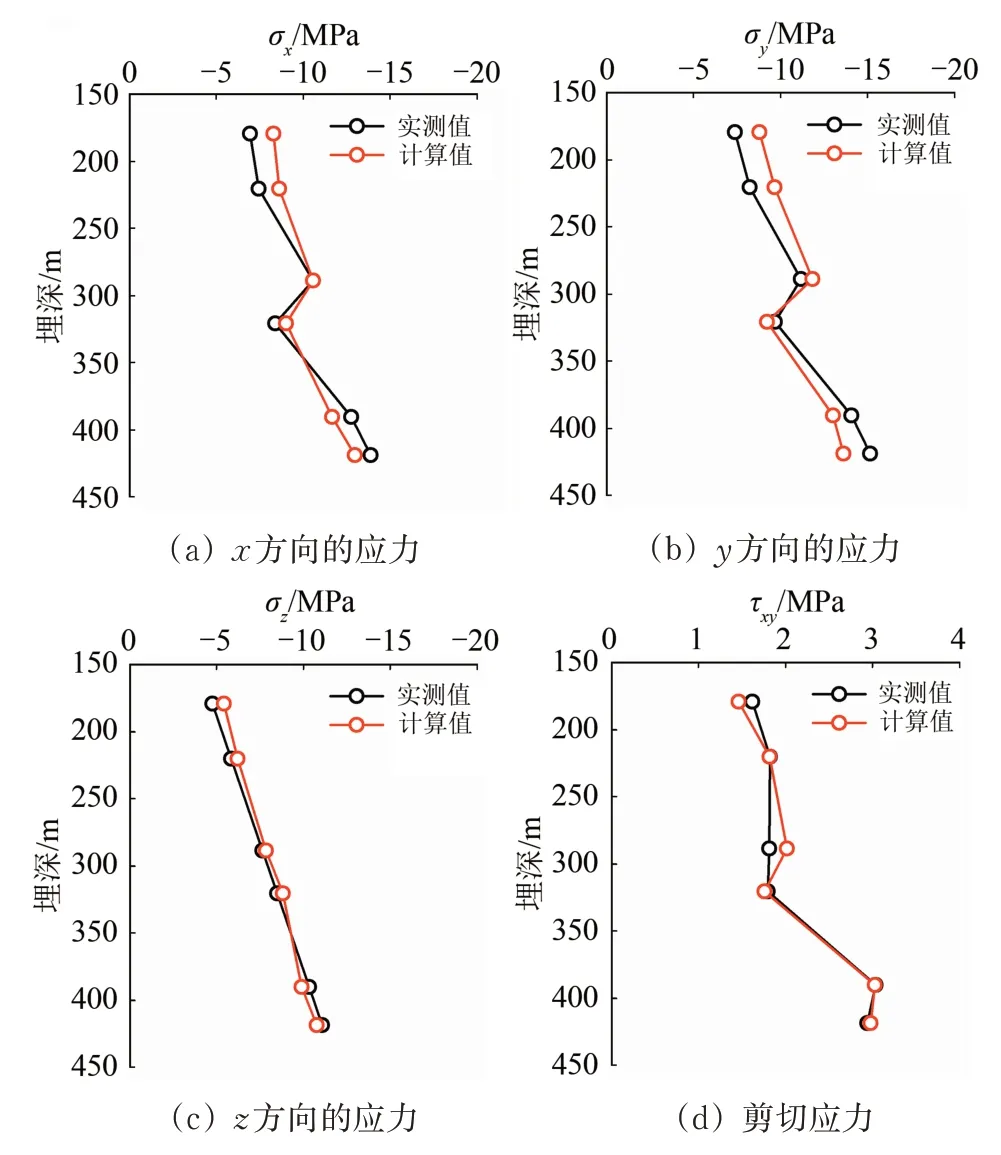
图4 应力实测值与计算值对比

由表6 和图4 可知：在数值大小上，应力计算值基本接近于应力实测值，仅少数测点存在较大差异，应力大小的最大残差为-1.54 MPa；其中垂直应力的计算值与实测值吻合最好，这是由于在水压致裂中获得的垂直应力是通过计算而来（ρi为第i层岩体的密度；g为重力加速度；hi为第i层岩体的厚度）。而在数值计算中也是通过相同的公式进行计算，故垂直应力的吻合度最高；方位角最大残差为-7.99°，残差较大，这是由于测点4位于白云岩夹泥岩的岩层中，白云岩夹泥岩较其他岩层的弹性模量有所降低，因此应力大小存在突变，见表3测点4对应的应力大小。

综上所述，应力计算值与应力实测值在数值大小上较为接近，沿隧道埋深的变化规律基本一致，表明反演得到的岩体初始地应力场是合理可靠的。

3 结 论

（1）在岩体初始地应力场反演过程中，p值法对回归模型的检验结果与F检验相同，对回归系数的检验结果与t检验相同；同时，p值法检验直接以p值与显著性水平α比较判断是否通过显著性检验，不需要与在给定显著性水平α下的临界值进行比较。可见p值法检验较F检验、t检验可更加直观方便地判断回归模型和回归系数是否满足显著性检验，且p值能够给出判断显著性的依据。因此，建议采用p值法检验判断回归模型和回归系数的显著性。

（2）p值表示反对原假设依据的强度，p值越小，则反对原假设的依据越强。因此可通过p值判断在自重和构造应力场中与岩体初始地应力场存在线性关系依据最强的应力场，从而验证反演结果的可靠性。若回归模型和回归系数对应的p值分别为p≤0.01，0.01＜p≤0.05，0.05＜p≤0.1，p＞0.1，则以所采用的回归模型反演岩体初始地应力场的依据分别是很强、强、弱、无。

（3）以斑竹林隧道为例，基于实测岩体初始地应力反演了岩体初始地应力场，并应用p值法检验、F检验、t检验验证了所采用回归模型和回归系数的显著性和可靠性。结果表明：应力计算值与实测值较为接近，沿隧道埋深的变化规律基本一致；反演得到的岩体初始地应力场是合理的、可靠的；通过p值可更充分地验证所采用回归模型的显著性和可靠性。