黏土中圆形低真空隧道管片结构内力分布及其影响因素

周建军，石 龙，王东元

（1.中铁隧道局集团有限公司 盾构及掘进技术国家重点实验室，河南 郑州 450001；2.西南交通大学 土木工程学院，四川 成都 610031）

利用磁悬浮技术减少轮轨摩擦和振动，构建低真空运行环境，减小空气阻力和噪声，成为未来更高速度轨道交通技术发展的重要方向之一，这种交通模式被称为第5 类交通模式［1-2］。现阶段，磁悬浮列车的低真空环境已发展出2 种模式，分别是地上高架管道和地下隧道。对于后者而言，其技术发展的关键在于能否在复杂的地下空间提供可靠安全的运行环境，而低真空环境下隧道管片结构的受力特性正是解决该问题的关键之一。

多年来，学者们针对盾构隧道管片结构在不同环境下的受力性能做了大量的相关性研究。例如，黄清飞等［3］将水位处于隧道断面的水压力按面积等效原则进行处理，根据力法方程推导了隧道管片结构的内力，并探讨了国内4种典型盾构隧道不同覆土条件下水位变化对管片结构内力的影响。谢红强等［4］以重庆主城排水过江盾构隧道为工程案例，基于现场监测数据，研究了施工期隧道周围外水压力的分布规律。梁东等［5］采用相似模型试验与数值模拟相结合的方法，研究了管片结构在发生侧向卸载时内力与变形的发展规律，以及管片厚度对这一过程的影响。戴志仁［6］以成都地铁为工程案例，利用有限元软件探究了地表大范围开挖卸载过程中下卧隧道的位移和内力的变化规律。方勇等［7］以兰州地铁为工程案例，基于室内模型试验，研究了强透水砂卵石地层中水压、土压、土体侧压力系数及拼装方式对管片结构受力特征的影响。何川等［8］以狮子洋隧道为工程案例，在模型试验与数值模拟的基础上，研究了大断面宽幅管片结构的三维内力分布规律。上述研究成果主要集中在常规大气压与高水压条件下，而真空环境下的管片结构受力性能鲜有研究。

隧道结构的分析模型大致包括地层—结构模型、荷载—结构模型、收敛约束模型及经验类比模型4大类［9-11］，但各有其适用场景与局限性，在具体实践中，已很少采用单一模型计算分析。当前较为常见的是荷载—结构法。该法根据管片接头力学处理方式及对纵向螺栓内力传递、管片接头刚度及外荷载分布形式等各种假设的不同，还可进一步分为均质圆环法、梁—弹簧模型法、梁—接头模型法和弹性铰圆环模型法［12-14］。修正惯用法属于均质圆环法中的1种，因其受力明确、计算思路清晰和简单实用等诸多优点，被广泛应用于盾构衬砌设计计算中［15-16］。

本文借鉴修正惯用法的思路构建力学模型，利用力法方程，推导得出可通用的圆形低真空隧道管片结构内力解析解。考虑建设地下低真空磁悬浮隧道的可行性，以武汉黏土为地层条件，分别基于荷载—结构、地层—结构这2种数值分析法，采用弹簧模型、修正剑桥模型，仿真模拟低真空隧道管片结构的内力。对比3种方法得到的内力，进一步分析圆形低真空隧道管片结构的内力分布特点，并探讨真空力、弯曲刚度有效率、地基抗力系数、侧向土压力系数等关键参数对管片结构内力的影响。

1 圆形低真空隧道管片结构内力—位移推导

假设低真空隧道管片结构的刚度均匀且连续（铰接部分和管片结构的刚度相同）［17-18］，在修正惯用法的基础上，构建圆形低真空隧道荷载模型，利用力法方程推导圆形低真空隧道管片结构的内力和位移。

1.1 基于修正惯用法的力学模型

文献［9］和文献［18］分别从不同的角度建立了圆形隧道管片结构内力分析模型。在他们的基础上，本文提出修正惯用法的圆形低真空隧道荷载模型，如图1 所示。图中：G为管片自重；p1为隧道真空力；p2为隧道顶部上覆土压力；p3和p4分别为隧道顶部和底部的侧向土压力，计算侧向土压力时采用水土合算；p5为侧向土体抗力；p6为地表附加压力；ph为隧道水平直径处的侧向土体抗力。

图1 基于修正惯用法的圆形低真空隧道模型及其荷载示意图

假设p5分布在隧道垂直方向45～135°范围内，并以抛物线图形垂直作用于隧道，那么p5的计算式［3］为

其中，

式中：φ为计算截面与隧道竖向直径之间的夹角；Ks为地基抗力系数；Δh为隧道水平直径处的土体变形。

1.2 管片结构的内力—位移推导

由图1 可知，隧道和周围荷载均对称于竖轴，因此沿竖向对称面的剪力为零，故隧道结构可简化为具有2 个多余未知力的超静定结构，如图2 所示。图中：ErIr为刚臂的弯曲刚度，在分析过程中假设刚臂在荷载作用下不发生变形，即认为刚度为无穷大；X1和X2分别为逆时针、水平方向的单位力；φ为竖向直径与管片截面之间的夹角。

图2 内力计算简化模型示意图

1）结构内力的推导

利用结构力学弹性中心法，将单位力X1和X2移至弹性中心（隧道圆心处），结合隧道竖向对称面处结构的水平位移与转角均为0，即可得到力法方程为

式中：δ11和δ22分别为在单位力X1和X2作用下，刚臂在作用点处沿X1和X2作用方向的位移；X1pi和X2pi分别为在荷载pi作用下产生的多余未知力；Δ1pi和Δ2pi分别为刚臂在荷载pi作用下沿着X1和X2作用方向的位移。

在计算力法主位移（δ11和δ22）和自由项（Δ1pi和Δ2pi）的过程中，考虑到弯矩对其影响显著，而轴力和剪力对其影响较小［19］，为计算方便，忽略式中后2项的影响，根据图乘法可得

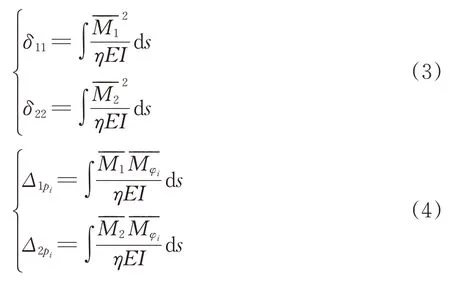
式中：η为弯曲刚度有效率，即等效均质环的弯曲刚度与管片主体截面弯曲刚度的比值；和分别为单独荷载X1、X2和pi单独作用下，简化模型截面φ处的弯矩。

隧道结构的内力是单位力X1，X2和荷载pi共同作用下的内力。利用力的叠加原理，可得到外荷载pi作用下隧道截面φ处的内力，即弯矩、轴力和剪力分别为

定义管片结构内力的方向：对于弯矩，使管片截面内侧受拉为正，外侧受拉为负；对于轴力，使截面受压为正，受拉为负；对于剪力，使截面顺时针旋转为正，逆时针旋转为负。因此，在单位力X1，X2和荷载p1的单独作用下，半径R的管片结构产生的内力分别为

将式（6）—式（8）分别代入式（3）和式（4），化简得到力法方程的主位移和自由项分别为

将式（9）和式（10）代入式（2），解得隧道真空力作用下的多余未知力X1p1和X2p1为

将式（11）代入式（5），求得p1作用下各截面的内力为

同理，可得其他荷载作用下各截面的内力，叠加得到各截面的总内力为

其他外力的推导与参考文献［9］一致，具体详细推导可参见该文献，本文不再展开。

2）结构位移的推导

假设在隧道断面中部作用1 个单位虚拟力S1，如图3 所示。利用结构力学中的位移法，通过式（14）和式（15），可得到各荷载pi作用下该处的水平位移和总位移。

图3 隧道腰部位移计算模型

由于初始计算时，隧道腰部水平直径处的土体变形Δh未知，因此本文通过迭代，计算得到侧向土压力ph，相应的计算流程如图4所示，图中ΔH为变量，即将计算得到的Δh赋值给ΔH。之后，便可进一步求解得到可通用的圆形低真空隧道管片结构内力解析解。

图4 真空隧道管片内力解析解计算流程

2 圆形低真空隧道管片数值模型

根据文献［20］给出的数据，以武汉黏土作为模拟地层，分别利用ANSYS19.0 和FLAC3D5.0建立荷载—结构模型和地层—结构模型，仿真计算不同工况下的圆形低真空隧道管片结构内力。地层常规参数包括：干密度γd=14.4 kN·m-3，饱和密度γsr=19.12 kN·m-3，土粒比重ds=2.73，含水率w=33.40%，地下水在地表下2 m 处。隧道的具体位置如图5 所示，图中：H为隧道埋深；D为隧道直径；h为地下水位。

图5 隧道位置示意图

2.1 荷载—结构数值模型

采用软件ANSYS19.0 中的静力分析模块，构建荷载—结构三维有限元模型如图6所示。管片结构采用Beam188 梁单元模拟，土体与管片结构的相互作用采用Combin14弹簧单元模拟。

图6 荷载—结构三维有限元模型

考虑到隧道管片周围的土体只能承受压力，但在数值计算过程中，部分弹簧存在受拉现象，与土体实际受力状态不符。因此，在模拟过程中启动单元的“生/死”功能（通过在模型中加入或删除材料，实现单元生/死功能），即当弹簧受拉时，赋予属性“死”，之后对调整的模型重新计算。

2.2 地层—结构数值模型

采用软件FLAC3D5.0，构建地层—结构数值分析模型如图7所示。土体采用对软土预测结果较为理想的修正剑桥模型（Modified Cam-Clay Model，MCC）［21］模拟，管片结构采用壳单元（Shell）模拟。

图7 地层—结构数值模型

修正剑桥模型所用到数据依旧沿用文献［20］。主要包括：临界状态斜率M=1.09，回弹参数κ=0.016 8，压缩参数λ=0.084 4，不排水抗剪强度cu=15 kPa，初始孔隙比e0=0.896，内摩擦角Φ=19.12°。前3 个参数的物理意义如图8 所示。图中：CSL为临界状态线（有效强度应力线）；NCL为正常固结线（各向等压初始加载曲线）；SL为回弹曲线（卸载回弹曲线）；p为平均主应力；q为偏应力；v为比容。

图8 剑桥模型临界状态线和固结曲线

FLAC3D中的壳单元被假定为3 节点构成的均厚度的三角形，管片可看作由大量壳单元组成。结合管片的常规尺寸和材料性质，壳单元的厚度取0.3 m，宽度取1.0 m，容重取24.5 kN·m-3。

3 圆形低真空隧道管片结构内力分布特点及影响因素

针对圆形低真空隧道管片结构，分别采用前文给出的基于力法的解析法（以下简称AM法）分析模型，以及基于荷载—结构法（以下简称SLM 法）和基于地层—结构法（以下简称SSM 法）的管片内力数值分析模型，分析圆形低真空隧道管片结构内力分布特点，探讨真空力、弯曲刚度有效率、地基抗力系数、侧向土压力系数等关键参数对管片结构内力的影响。

3.1 条件假定及工况选取

1）条件假定

真空隧道超高速运行的安全性能是其投入商业运营的关键，考虑到单管双线隧道中列车近距离运行风险性较大，实际工程采用单管单线隧道的可能性更大，故以单线隧道管片为例进行分析，管片的外径R、宽度b和厚度t取常用规格，分别为2.85，1.00，0.30 m，隧道埋深10.00 m。

考虑到真空隧道对运行环境的气密性具有较高的要求，而混凝土的气密性与强度呈正相关，故本文采用《铁路隧道设计规范》中给出的最高强度等级C50混凝土，其弹性模量E=3.45×104MPa。

2）工况选取

真空隧道管片内力受多种因素的影响，选取对其影响最为关键的真空力、弯曲刚度有效率、地基抗力系数和侧向土压力系数等因素进行分析。为便于参数对比，在上述假定条件的基础上，设计10种工况，各工况主要参数取值详见表1。

表1 各工况主要参数取值

工况1—工况3 主要分析真空力p1对管片结构内力的影响。p1值分别取0，50，100 kPa，其中p1=0代表常规隧道，p1=50 kPa代表隧道内压力为0.5个大气压的低真空隧道，p1=100 kPa 代表近似完全真空隧道，其他参数不变。

工况4—工况6 主要分析弯曲刚度有效率η对管片结构内力的影响。相关研究表明η通常取值在0.10～0.90 之 间，本文分别取值0.20，0.50 和0.80进行分析，其他参数不变。

工况8、工况7 和工况4 主要分析地基抗力系数Ks对管片结构内力的影响。根据工程经验，软土中Ks在3～30 MPa·m-1之间，本文分别取值5，15，30 MPa·m-1进行分析，其他参数不变。

工况9、工况4、和工况10 主要分析侧向土压力系数Ka对管片结构内力的影响。本文分别取值0.35，0.50和0.65进行分析，其他参数不变。

3.2 完全真空隧道管片结构内力分布特点

真空力越低，列车受到的气流阻力越小。在技术可行的条件下，完全真空隧道是列车减阻最为理想的运行环境。为认识完全真空隧道管片的内力分布特点，以工况3 为例，将其计算参数代入3 种模型，计算隧道管片结构的内力分布，如图9 所示，由图可以得出如下结论。

（1）除了弯矩为0 处，3 种方法计算得到的隧道管片结构均处于偏压状态，其中顶部与底部为内侧受拉，腰部为外侧受拉。值得注意的是，顶部与底部附近的正弯矩相对较大，腰部的负弯矩相对较大，而轴力相对较大的位置在腰部。

（2）3 种方法得到的管片结构弯矩和轴力分布曲线基本一致，但细节上存在差异。①对于管片弯矩，AM 法与SLM 法求得的结果较为接近，SSM法则偏小；但无论正弯矩、负弯矩，都是AM法求得的峰值绝对值最大，SLM 法次之，SSM 法最小。②对于管片轴力，在腰部以下位置，3 种方法结果相差不大；在腰部以上位置，SSM 法计算结果明显大于其他2 种方法。③进一步观察轴力峰值，SSM 法求得的结果最大，SLM 法次之，AM法最小；轴力峰值分布位置则有不同，SLM 和AM 法的位置几乎重合，均为90°附近；SSM 法则位于70°附近，与前者相差约20°。

图9 工况3条件下按3种方法计算的隧道管片结构内力分布

产生上述差异的可能原因如下：SLM 和AM法中，假定作用在管片上的主动荷载为线性分布，而实际上并非如此，SSM 法中主动荷载的分布更接近实际分布；SLM 和AM 法中，管片与围岩之间的相互作用采用弹簧模拟，且抗力与变形呈线性关系，而实际上两者间关系为非线性；SSM 法一定程度上考虑了管片顶部土体的土拱效应，SLM和AM法则并未考虑这点，而是直接采用土柱高度计算竖向压力；AM 法中假定抗力分布在45°～135°范围内，实际上抗力分布范围与土体变形范围密切相关。

上述结果表明，低真空隧道管片结构的控制截面在隧道顶部、底部和腰部。由于3种方法的假定条件和计算原理不同，导致最终的计算结果也存在一定的差异。总体而言，AM 法得到的结果具有较高可信度，且内力计算过程简单明了，但其结果偏于保守；SLM 法建模过程复杂、耗时长，但在地层参数取值正确的条件下计算结果最为精确；SSM 法所需参数少，计算速度也相对较快，但计算结果偏于危险。

3.3 真空力对管片结构内力的影响

真空力直接影响着管片结构的内力分布。为分析真空力带来的影响，选取仅真空力条件不同的3种工况（工况1—工况3），分别计算隧道管片结构的内力分布，如图10 所示。图中：SLM-工况1 表示真空力为0 kPa 作用下，载荷—结构法求得的管片内力。其余标识含义按此类推。

图10 真空度对管片结构内力的影响

由图10 可以看出：真空力的变化对作用在管片结构上的弯矩几乎没有影响，但对轴力的影响非常明显，与常规隧道（p1=0 kPa）相比，对于近似完全真空隧道（p1=100 kPa）的单宽截面，其轴力增大的幅度在数值上约等于其半径与1个大气压的乘积。

上述结果表明，真空力的存在可以削减其他荷载在管片上产生的拉应力，从而减轻或减少管片受拉侧混凝土的张拉裂缝，一定程度上提高管片结构工作时的完整性，有利于改善管片结构的渗透性和气密性。

3.4 弯曲刚度有效率对管片结构内力的影响

为分析弯曲刚度有效率的影响，选取仅弯曲刚度有效率不同的3 种工况（工况4—工况6），分别计算隧道管片结构的内力分布，如图11 所示。图中：SLM-工况4表示在η=0.8条件下，载荷—结构法求得的管片内力。其余标识含义按此类推。

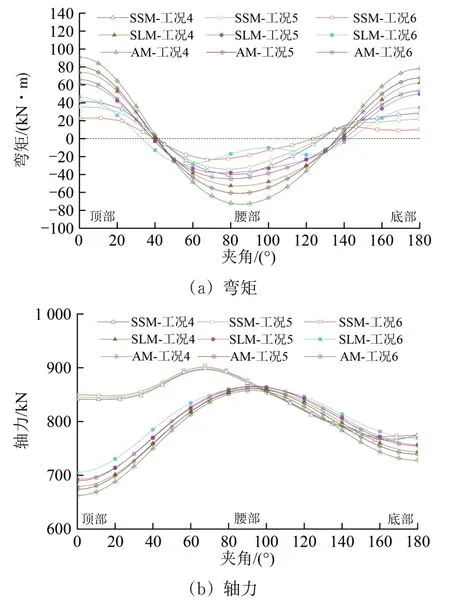
图11 弯曲刚度有效率对管片结构内力的影响

由图11 可以看出：弯曲刚度有效率对管片结构承受的弯矩和轴力的影响相反，随着弯曲刚度有效率的增加，弯矩曲线逐渐趋于陡峭，总体上，弯矩呈递增趋势，但轴力呈递减趋势；值得注意的是，因计算方法的不同，同一截面处内力随弯曲刚度有效率的变化幅度存在差异，SSM 法得到的内力变化幅度最小，SLM 法和AM 法比较接近；此外，同1种方法得到的结果，弯矩与轴力的增减幅度的分布存在差异，隧道腰部、顶部和底部的弯矩增幅较大，轴力增幅较大位置则在顶部和底部，且从顶部和底部向腰部呈递减趋势。

上述结果表明，在变形允许的情况下，可以适当降低管片结构的刚度，从而减小管片承受的内力，达到优化管片结构的目的。

3.5 地基抗力系数对管片结构内力的影响

为分析地基抗力系数的影响，选取仅地基抗力系数条件不同的3 种工况（工况4、工况7、工况8），分别计算隧道管片结构的内力分布，如图12所示。图中：SLM-工况4表示在Ks=30 MPa·m-1条件下，载荷—结构法求得的管片内力。其余标识含义按此类推。

由图12 可以看出：地基系数对管片承受的弯矩和轴力的影响存在差异；管片的弯矩随着地基系数的增大分布曲趋于平缓，即正、负弯矩的绝对值均在减小，但减幅随截面位置发生了变化，腰部、顶部和底部附近的截面减幅较大；轴力随着抗力系数的增大整体上呈递增趋势，增幅自腰部向顶部和底部逐渐递增。

上述结果表明，可以通过围岩注浆等措施提高土体抗力系数来减小管片结构弯矩、增加管片轴力，从而在一定条件下增加管片的承载能力。

3.6 侧向土压力系数对管片结构内力的影响

为分析侧向土压力系数的影响，选取仅侧压土压力系数条件不同的3种工况（工况4、工况9、工况10），分别计算隧道管片结构内力分布，如图13所示。图中：SLM-工况4 表示在Ka=0.50 条件下，载荷—结构法求得的管片内力。其余标识含义按此类推。

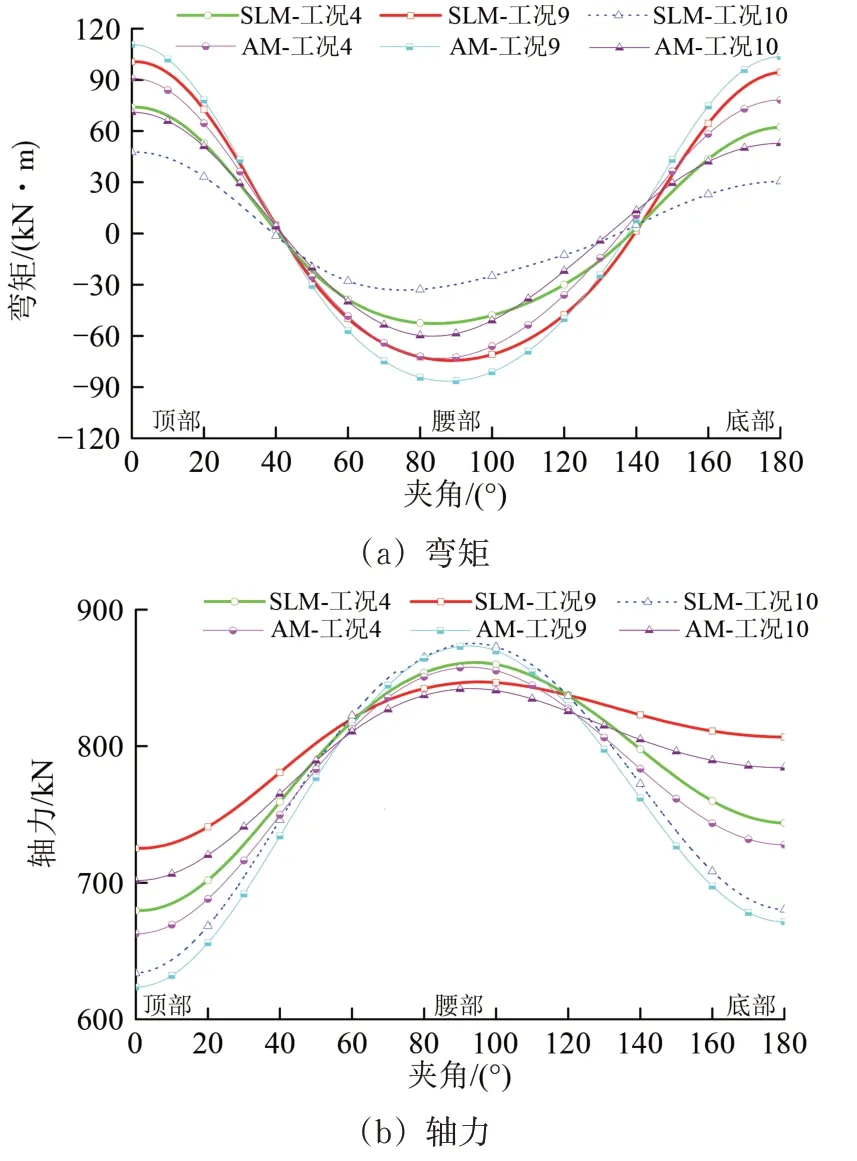
图13 土体侧压力系数对管片结构内力的影响

由图不难看出：管片结构的弯矩绝对值随着侧压力系数的增大而逐渐减少，减幅较大位置位于顶部和底部截面附近，这与地基抗力系数对管片结构弯矩的影响类似；而轴力变化明显不同于弯矩，在66°～115°截面之间，随着侧压力系数的增大而减小，其余截面则相反，且减幅较大位置在腰部，增幅的较大位置在顶部和底部。

4 结 论

（1）通过力法方程推导得到了圆形低真空隧道管片结构内力的解析解，并将特定工况下的解析解与荷载—结构、地层—结构2 种模型的数值解进行对比，发现三者间具有较好的一致性，证实解析解具有较高可信度。

（2）以武汉黏土作为模拟地层，发现圆形低真空隧道的管片结构大部分截面处于偏压状态，腰部附近的截面外侧受拉，顶部和底部附近的截面内侧受拉；低真空隧道管片结构正弯矩较大的位置在隧道顶部与底部，负弯矩与轴力较大的位置在腰部。

（3）对于黏土中的圆形低真空隧道，真空力对管片结构弯矩几乎没有影响，但对轴力影响非常显著，并随真空力的增大而增大。

（4）对于黏土中的圆形低真空隧道，管片结构弯矩随着弯曲刚度有效率的增大呈递增趋势，随地基抗力系数和侧向土压力系数增大呈递减趋势，弯矩的增幅较大的位置均分布在隧道顶部、底部和腰部。

（5）对于黏土中的圆形低真空隧道，管片结构轴力随地基抗力系数增大呈递增趋势，随弯曲刚度有效率增大呈递减趋势；在隧道腰部附近，轴力随土体侧压力系数的增大呈递减趋势，在隧道底部和顶部附近则相反。