精细全光谱结合GS-SVR的复杂水体硝酸盐分析方法研究

雷会平，胡炳樑，于 涛*，刘嘉诚，李 炜，王雪霁，邹 妍，史 倩

1.中国科学院西安光学精密机械研究所,陕西 西安 710119 2.中国科学院大学光电学院，北京 100049 3.山东省科学院海洋仪器仪表研究所，山东 青岛 266000

引 言

水是人类社会生产生活与持续发展必不可少的资源[1]。硝酸盐是水质健康状态评价的一个关键要素，过高浓度的硝酸盐一旦流入水体环境就会刺激藻类快速繁殖，致使水体恶化，进而造成物种多样性剧减以及生态环境的破坏，如果被人体误摄，会引起“高铁血红蛋白症”。因此，实现水体硝酸盐的高精度快速实时在线监测对于水务事业的安全保障与水污染的预警防治极具重要的科学意义和社会价值。

基于光学测量的水质在线监测方法是当前及未来水环境动态监测的发展趋势[1]。相较于传统硝酸盐现场采样加实验室化学分析的测定方法，其具有操作便捷，无需前处理，检测效率高，重复性好且无二次污染等显著优点，非常适合水环境中硝酸盐的快速在线监测，在直饮水，地表水，废水的在线检测等方面具有广阔的发展前景。针对水体组份解析算法，常见的有单波长法，双波长法，偏最小二乘法(partial least square,PLS)，人工神经网络法(artificial neural network,ANN)，支持向量机法(support vector machine，SVM)。Jean Causse[2]和Pons[3]等采用连续光谱二阶导数测定淡水中硝酸盐和溶解有机碳，并在多个淡水样品中验证了该方法的可靠性。宓云軿等[4]依次采用PLS，SVM和LM-反向传播神经网络(back propagation neural network，BPNN)建立吸光度与化学需氧量(chemical oxygen demand,COD)间的浓度模型，结果验证SVM，LM-BPNN等回归模型的预测效果显然优于PLS。倪雪春等将支持向量回归机(support vector regression,SVR)运用于混合重叠的光谱分析中，实现了硝酸盐含量的浓度预测。王莉丽等[5]研制了一种新型的海水硝酸盐检测系统，结合PLS法进行硝酸盐浓度与吸收光谱间的相关性分析，实现了海水硝酸盐的在线检测。杨琼[6]等结合近红外光谱以及后向间隔偏最小二乘(back interval partial least square,BiPLS)法对生活废水中的COD回归建模，结果显示预测效果优于PLS建模。刘思乡等利用主成分分析对原始光谱数据降维，然后使用局部加权线性回归建模，获得了较好的预测结果。陈颖等[7]提出了一种基于光谱的混合回归预测模型，包括双波长法与最小二乘支持向量机法，将溶液样本分为高浓度样本和低浓度样本两部分，验证结果良好。

但是，实际水体组分更加复杂与多元化，水体参数和吸光度二者并非呈现线性相关，使用线性回归模型难以达到满意的预测效果，所以必须建立非线性的预测模型。ANN建模预测难以克服预测结果的不稳定性，而SVM因其在小样本、非线性、高维问题中的优势获得广泛关注。本文结合精细全光谱技术，提出一种基于改进的网格搜索(grid search,GS)方法优化SVR以期完成建模预测，并与传统预测模型的结果加以对比，结果验证，提出的算法在预测精度以及训练效率方面都有显著提升。

1 基本原理

1.1 支持向量回归思想

SVM基于结构风险最小化原理，可以有效地应对实际应用情境下出现的小样本、非线性和高维问题[8]，具有良好的性能和预测精度。SVR的基本思路是把原始数据x非线性映射到高维特征空间，然后在此空间中解决线性回归问题。SVM的回归函数为

f(x)=wφ(x)+b

(1)

其中φ(x)为特征空间，是权重向量，b是偏差项。系数和b则由风险函数最小化来估计

(2)

(3)

式(3)中，若预测误差小于ε，则损失为零，否则损失超出范围。引入两个正松弛变量ξ和ξ*表示从实际值到相应边界值的距离。将式(2)转化为式(4)

(4)

约束条件为

(5)

该优化问题通过式(6)求解

(6)

约束条件为

(7)

(8)

因此，回归函数为

(9)

式(9)中，K(xi,x)为核函数，其值为K(xi,x)=Φ(xi)Φ(x)。在SVM中，径向基核函数(RBF)K(xi,x)=exp(-‖xi-x‖/2σ2)仅须确定一个变量，便于参数优化。此外，其构造的SVR具有良好的非线性预测性能。因此，将RBF应用于SVR中。

1.2 改进的网格搜索法

据实际应用情况，参数设置和核函数的选择对SVR的学习和泛化性能影响很大[9]。网格搜索(grid search,GS)是一种直接的参数优化算法，用于确定SVR的最佳参数值[10-11]。通过设置搜索中的上下界(搜索间隔)和跳跃间隔的适当值，使得优化算法遍历网格中的每一个参数组合，并采用交叉验证技术作为性能度量找到最优参数组合。实际操作中往往设置较大的搜索范围和较小的搜索间隔，因此，参数寻优的过程会占用大量时间，导致模型效率低下。本文提出了多次变步长的网格搜索算法对SVR模型参数进行调整，具体操作步骤如下：

(1) 初始化参数搜索范围及搜索步长，在初始的网格搜索范围中，将预先设置的参数组合搜索步长扩大T倍，进行第一次参数寻优。

(2) 依据图1的参数搜索空间确定流程，将C与σ的搜索范围缩小，并且缩小搜索步长F倍，继续第二次参数寻优。具体流程如图1。

(3) 依据图1的参数空间确定流程，把C与σ的搜索空间再次缩小，同时把它的步长缩小S倍，继续进行参数寻优。其中T=FS。

图1 参数搜索空间的确定Fig.1 Determination of parameter search space

(4) 将(3)中获取的最优参数组合代入SVR模型，建立训练集吸光度光谱数据与硝酸盐浓度的数学模型。

(5) 将测试集应用于步骤(4)获取的回归模型完成预测，输出测量结果。

通过以上操作，将原本的搜索空间减小并多次改变步长，简化了计算，大幅提升了寻优效率。

2 实验部分

2.1 数据获取

使用自研光谱仪采集溶液的原始透射光谱数据，并将其转换为吸光度光谱数据，然后基于可变步长的网格搜索法进行模型参数寻优，将获得的最优参数组合应用于SVR模型，建立训练集吸光度光谱数据与硝酸盐浓度间的数学模型，然后利用该数学模型完成测试集的浓度预测。总体流程图如图2所示。

图2 实验整体流程Fig.2 Overall flow of the experiment

2.2 样本溶液

溶液样本的配制在陕西科技大学化学与化工学院实验室内完成。采用标准的硝酸盐溶液，铂-钴标准溶液，福尔马肼标准混悬液根据实验要求按照不同的浓度梯度配置了94组不同浓度的溶液样本。硝酸盐、浊度、色度的浓度量程分别为7～15 mg·L-1，0.5～5 NTU，7～15度(铂-钴色度单位)，浓度间隔分别为1 mg·L-1，0.5 NTU，1度。每一个待测溶液样本的三种组份浓度配比为随机生成。

2.3 装置

实验装置采用光源，光源衰减器，比色皿，光谱仪和计算机组成的集成系统获取被测物质的透射光谱。样本溶液光谱数据的采集装置选取了项目组自主设计研发的双光路主动校正连续光谱仪，原理如图3所示。该装置使用双光路主动校正结合连续光谱精细获取的方法，相对于传统的单光路连续长时间作业的系统误差校正进行了去除。自研仪器的光谱范围：185～1 100 nm，光谱分辨率：1.5 nm，闪耀波长：250 nm，共含3 648个像素点。

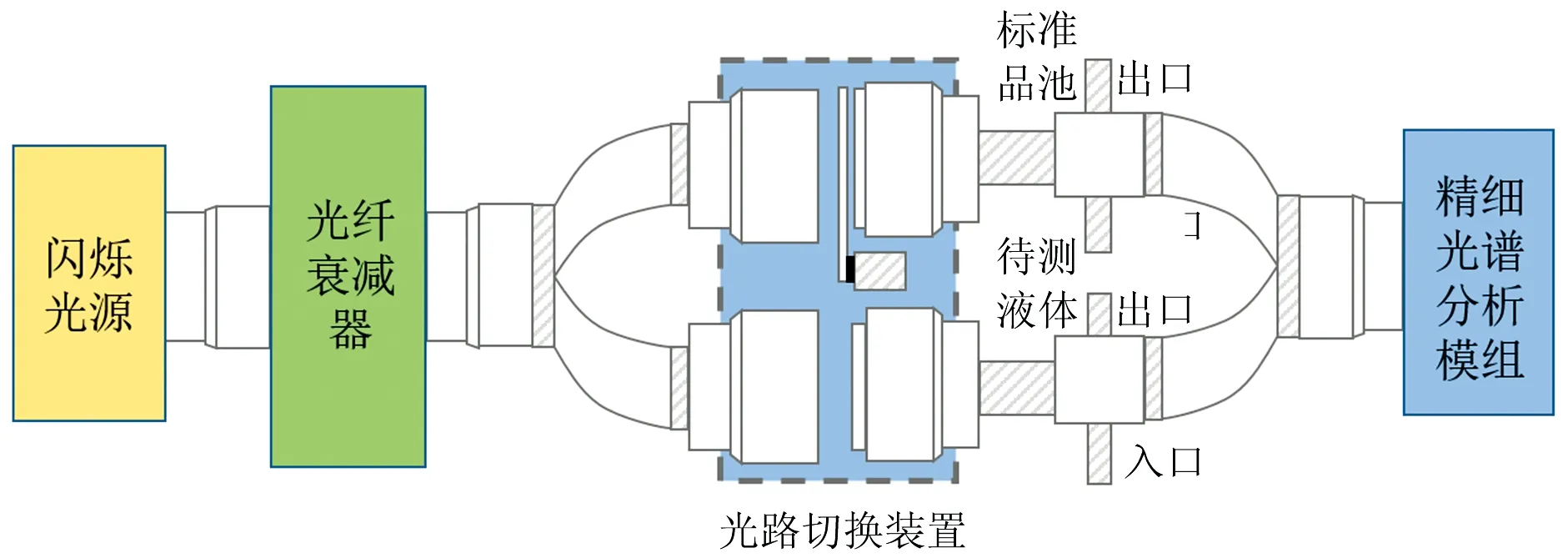
图3 光谱法主要测量技术原理图Fig.3 Main measurement technology schematic diagram of spectrometric method

将被测溶液的原始透射光谱数据转换为吸光度光谱数据，所有样本溶液的吸收光谱图如图4所示。

图4 94个不同浓度溶液样本的吸收光谱Fig.4 Absorption spectrum of 94 samples with different concentrations

2.4 样本分类

对待测溶液的吸光度数据进行建模预测之前，使用Kennard-Stone算法将其划分为训练集和测试集，其划分原则是把已选取的样本点与其余样本点间的最小直线距离最大化。样本i与样本j间的欧氏距离定义如式(10)

(10)

式(10)中，rik与rjk分别为样本i和样本j在波长k处的吸光度，p为待测样品溶液光谱的波段数。通过上述算法94个溶液样本被划分为80个训练样本与14个测试样本。

3 结果与讨论

3.1 改进GS-SVR的参数寻优

改进的GS法通过多次减小参数的搜索空间以及修正步长大幅提高了参数寻优速度，配合交叉验证法进行训练集的建模，将获得的最优的C和σ参数再用于测试样本的浓度预测。惩罚参数C取值范围设为[2-9，29]，σ取值范围设为[2-10，210]，二者的搜索步长初始设为0.5，依次将其扩大10倍，缩小2倍，缩小5倍，选择RBF核函数，得到三次参数寻优的均方误差的3D视图如图5，图6，图7所示。

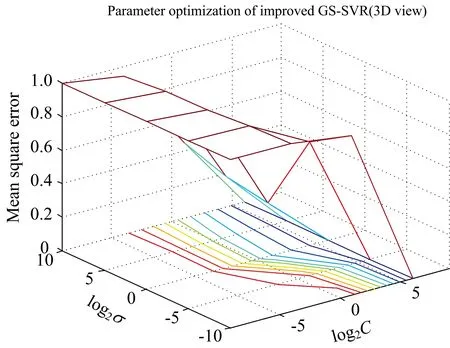
图5 改进GS-SVR第一次参数寻优3D视图Fig.5 3D view for the first parameter optimization of Improved GS-SVR

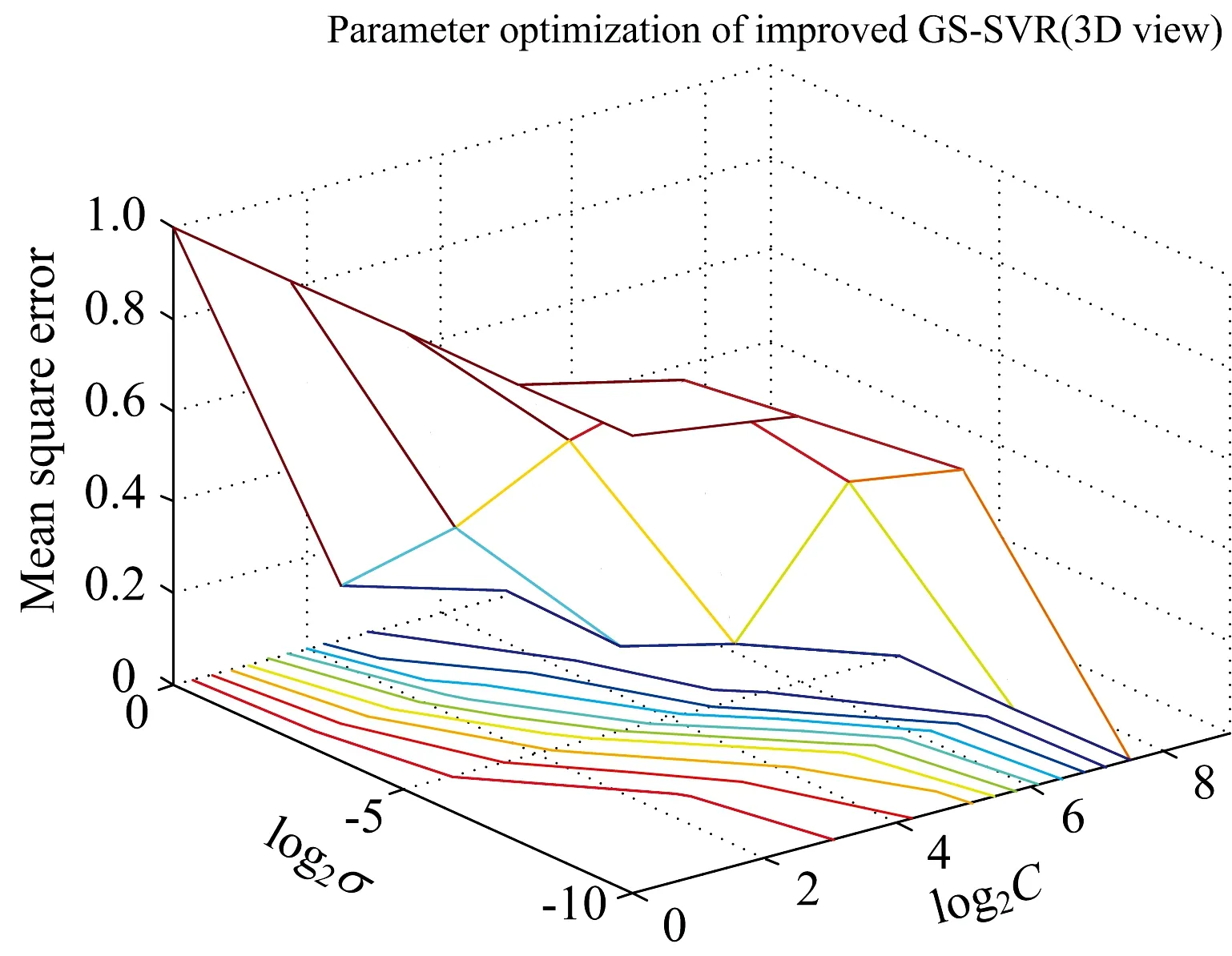
图6 改进GS-SVR第二次参数寻优3D视图Fig.6 3D view for the second parameter optimization of Improved GS-SVR

由图5—图7可知，每一次改变步长后参数搜索空间都会缩小，降低了参数选择的计算量，克服了传统方法非常耗时的缺陷。

图7 改进GS-SVR第二次参数寻优3D视图Fig.7 3D view for the third parameter optimization of Improved GS-SVR

3.2 改进GS-SVR建模预测

将3.1节三次参数寻优的最优参数C和σ组合(512，0.044 2)应用于支持向量回归模型，最终获得测试集的预测效果如图8(a)所示，预测结果的相对误差(relative error,RE)如图8(b)所示。

图8 (a) 改进GS-SVR预测值与真实值对比; (b) 改进GS-SVR预测值相对误差Fig.8 (a) Comparison between the predicted value of improved GS-SVR and the real value；(b) Relative error of the predicted value of improved GS-SVR

图8和图9分析可知，改进的GS-SVR建模的预测效果较好，其中回归模型的决定系数(coefficient of determination)R2=0.993 5，预测均方根误差(root mean square error of prediction，RMSEP) RMSEP=0.043 5。14个样本预测值的绝对误差(absolute error,AE)控制在0.5以内，最大AE是0.465 1，一半样本的AE不超过0.1。预测值的相对误差最大3.32%。整个过程平均花费时间为13 s，满足快速监测的应用需求。

图9 (a) 不同预测模型的预测值与真实值对比;(b) 不同预测模型的预测值相对误差Fig.9 (a) Comparison between predicted value and real value of different prediction models； (b) Relative error of predicted values of different prediction models

基于吸光度光谱数据，同时建立了BPNN，SVR，GS-SVR，PSO-SVR，GA-SVR五种预测回归模型，与文中提出的可变步长GS-SVR方法加以对比。每种模型训练5次，在表1中统计了硝酸盐浓度预测模型的R2，RMSEP，训练时间。

表1 不同预测模型评价参数对比Table 1 Comparison of evaluation parameters of different prediction models

分别从预测精度，预测误差，训练效率以及稳定性四个方面来对比六种预测模型的性能。由表1 分析可知，相比于BPNN，SVR，GS-SVR，PSO-SVR，GA-SVR五种预测回归模型(取5次预测精度最高的对比)，改进GS-SVR预测精度最高，R2=0.993 5，分别提高了1.22%，11.66%，0.78%，0.74%和0.77%。RMSEP=0.043 5，分别降低了-4.36%，1 644%，308%，80%和112%。改进GS-SVR平均训练时间为13 s，相较BPNN的67 s，GS-SVR的121 s，PSO-SVR的291 s，GA-SVR的146 s，效率分别提升了4.15倍，8.30倍，21.38倍，10.23倍，尽管SVR模型训练时间最短，但其精度不高，且误差很大。GS-SVR，PSO-SVR，GA-SVR模型存在一个明显的缺陷就是计算量大，训练效率较低，需要等待很长时间才能完成一次参数的解算，参数寻优过程耗时过长，尤其后两者预测结果不稳定，容易陷入局部极优。BPNN的最大缺点就是预测效果极不稳定，效果较好时R2高达0.981 5，训练效果较差时，R2只有0.715 4。究其原因，BPNN是局部搜索的优化算法，在计算非线性函数的全局极值时极大概率陷入局部极值，导致训练精度降低。同时，网络结构的选取尚无成熟的理论指导，只能凭经验进行选择，因此如何采用合适的网络结构也是BPNN预测模型训练的关键问题。比较可知，改进的GS-SVR模型综合预测精度，预测误差，训练效率以及稳定性方面皆优于其他模型，在提升预测精度的同时提高了算法的优化效率。

六种硝酸盐浓度回归模型的预测结果与真实值如图9(a)所示，相对误差如图9(b)所示。改进GS-SVR最大绝对误差控制在0.5以内，0.465 1(改进GS-SVR)<0.729 7(GS-SVR)<0.755 1(PSO-SVR)<0.865 9(GA-SVR)<0.874 1(BPNN)<1.830 3(SVR)，为六种模型中最优。相对误差为3.32%(改进GS-SVR)<5.77%(PSO-SVR)<6.18%(GA-SVR)<8.30%(GS-SVR)<8.84%(BPNN)<14.12%(SVR)，无论是绝对误差还是相对误差，改进GS-SVR模型都保持在最低水平，预测效果明显优于其他五种模型。

4 结 论

基于精细全光谱结合支持向量回归技术提出了一种基于可变步长的GS法优化SVR，将其用于混合水体硝酸盐浓度的建模预测。通过可变步长的GS寻优算法获得最优参数C和σ为(512，0.044 2)，建立SVR硝酸盐浓度预测模型，模型R2=0.993 5，RMSEP=0.043 5，平均训练时间为13 s。并同目前流行的BPNN，SVR，GS-SVR，PSO-SVR，GA-SVR算法对比，R2分别提高了1.22%，11.66%，0.78%，0.74%和0.77%，训练效率分别提升4.15倍(BPNN)，8.30倍(GS-SVR)，21.38倍(PSO-SVR)，10.23倍(GA-SVR)。结果显示，提出的GS-SVR方法不仅提高了模型的预测精度，而且在寻优效率方面取得了很大的提升，可为复杂基质水体硝酸盐浓度的快速在线监测提供一种新的有效方法，具备潜在的应用价值。