RAT矩函数在模态振形数据去噪中的应用

张浩，臧朝平

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

矩函数数据去噪是最常用的形状特征提取方法，最初矩函数主要应用在图像识别领域。随着研究的深入，在结构动力学领域矩函数也得到了广泛的应用。图像处理中最常用的矩函数为TEAGUE M R[1]提出的Zernike矩和Legengre矩两个具有正交性的二维矩函数，可以解决几何矩造成信息冗余的问题。但由于上述矩函数为连续函数，因此在计算时使用离散求和的方式，这样不可避免地带来很大的计算误差。随后MUKUNDAN R[2]提出了一个离散的矩函数，即Tchebichef矩函数。Tchebichef矩要优于Zernike矩与Legendre矩。因为Tchebichef矩是离散的正交矩，不仅能够避免数据的冗余，还能消除连续积分离散化带来的误差。

基于矩函数能够压缩振型数据并反映结构的振动信息，王耀明[3]最早将Tchebichef矩函数引用在动力学模型确认中，并完成了对二维矩形、圆形结构的振型描述。但是二维矩函数在处理三维结构时只能使用投影等降维的方式，这样不仅操作复杂，还会造成几何信息的缺失。为了解决这个问题，曾亚未等[4]构建了三维的径轴向Tchebichef矩函数(RAT矩)。但是由于RAT矩函数是定义在柱坐标下的矩函数，其只能够描述三维圆柱结构的模态振型。

在工程中大多数航空发动机部件为变截面的曲面结构,马健等[5]采用径向坐标r的多项式去拟合轴向坐标z的方法，从而实现描述简单的三维曲面机匣的模态振型，但该方法不具有通用性。本文作者采用积分的思想，将曲面机匣当作由若干圆柱机匣积累而成，并将振型数据插值到一个圈数×点数×层数的像素空间内。这样就可以使用RAT矩函数直接描述三维曲面结构的模态振型[6]。

在工程实际中，如何保证测试数据的准确性一直都是需要研究的问题。在测试过程中会有很多因素影响测试结果的准确性，最常见的是试验过程中噪声的影响。若测试过程中存在很大的噪声，会导致试验数据准确性降低。基于RAT矩函数对曲面结构的振型描述能力，进一步研究了RAT矩函数在去噪中的应用。采用正态分布的随机噪声模拟实际噪声影响，分析了不同噪声强度下RAT矩函数的去噪能力，对将矩函数应用到工程试验的去噪过程有重要意义。

1 RAT矩函数的模态振型描述方法

1.1 矩变换

在描述三维结构的模态振型时，将每个节点的位移看作每个像素点的灰度值，将振型数据表示为I(x,y,z)，每一个点(x,y,z)对应一个位移值I(x,y,z)。从而利用三维矩函数能够实现对振型数据的矩变换，矩变换可表示为

ϑ=Γ[I(x,y,z)]

(1)

式中：I(x,y,z)代表模态振型函数；Γ[*]表示对振型数据进行矩变换的过程，该过程可具体表示为

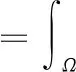
(2)

其中：ϑ(x,y,z)表示三维矩函数，如本文使用的Radial Axial Tchebichef矩函数；Ω为矩函数自变量的取值范围。

1.2 RAT矩函数的振型描述

RAT矩函数的表达式见如下：

(3)

其中：p=0，1，…，(N/2-1) 表示径向的阶数；q=0,1,…，m-1 表示重数；l代表的是轴向的阶数,l=0,1,…,(N/2-1)；r、k、z分别是径向坐标、周向坐标和轴向坐标；tl,h(z)和tp,m(r)分别表示轴向与径向的Tchebichef多项式，表达如下：

(4)

(5)

对结构的振型图像进行矩变换，从而提取出特征矩集，该过程能够实现对庞大振型数据的压缩处理，特征矩集的表达式见式(6)。

(6)

1.3 基于特征矩集的振型重构

通过从振型数据中提取出的特征矩集能够重构振型图像，重构公式如下：

(7)

引入一个总体相似度系数(GSC)的概念去评价重构振型与参考振型的相似程度，GSC的表达如下：

(8)

式中：Ω代表振型数据的定义域范围；I′和I分别为重构的振型与原始的振型，另外：

(9)

GSC的定义如下：

(10)

GSC(i)代表RAT矩的阶次为i时的每一阶模态重构振型与原始振型的总体相似度系数；Smean,i与Svar,i分别为为每一阶模态的重构振型图像与原始振型图像相似度的均值与方差。GSC的取值在0～1之间，数值越大则代表重构精度越高。

2 RAT矩函数对仿真模型的振型描述与去噪分析

为了验证RAT矩函数对三维曲面机匣的模态振型描述能力与抗噪性，以一个三维曲面结构的有限元模型为例，材料采用GH4169高温合金，结构的弹性模量E为204GPa，密度为8240kg/m3，泊松比为0.3。在ANSA中使用二阶四面体单元对机匣划分网格，共有26195个节点，12851个单元。使用Nastran求解器对该模型进行模态计算，计算自由-自由状态下的前10阶模态。

2.1 RAT矩函数对的振型描述能力

图1 曲面机匣有限元模型

建立的有限元模型见图1。将振型数据插值到一个圈数×点数×层数的三维像素空间内，构建其模态振型图。构建的前8阶模态振型图见图2。利用RAT矩函数对该有限元模型的振型数据进行矩变换，得到每一阶模态的特征矩集，每一阶的特征矩集见图3。利用提取出的RAT特征矩集可以对振型图像进行重构，重构振型图见图4。

观察原始振型图与利用RAT矩函数重构的振型图，可以看到重构振型图的精度非常高，与原始振型图基本一致，证明了RAT矩函数对三维曲面结构模态振型图的描述能力。

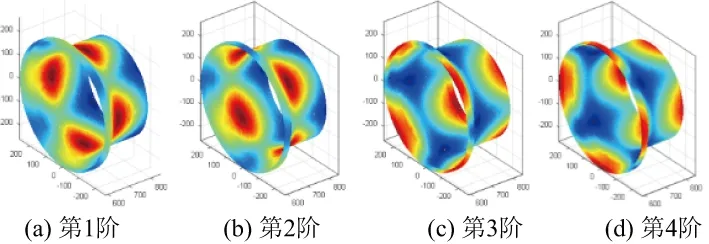
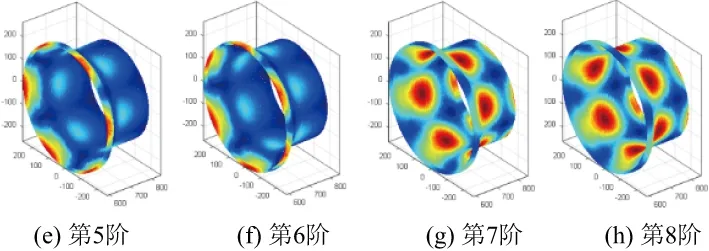
图2 有限元模型的前8阶模态振型

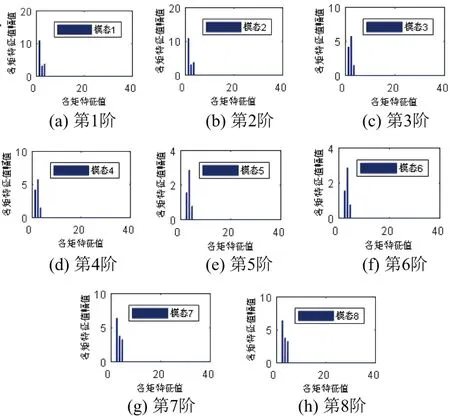
图3 每一阶的特征矩集幅值

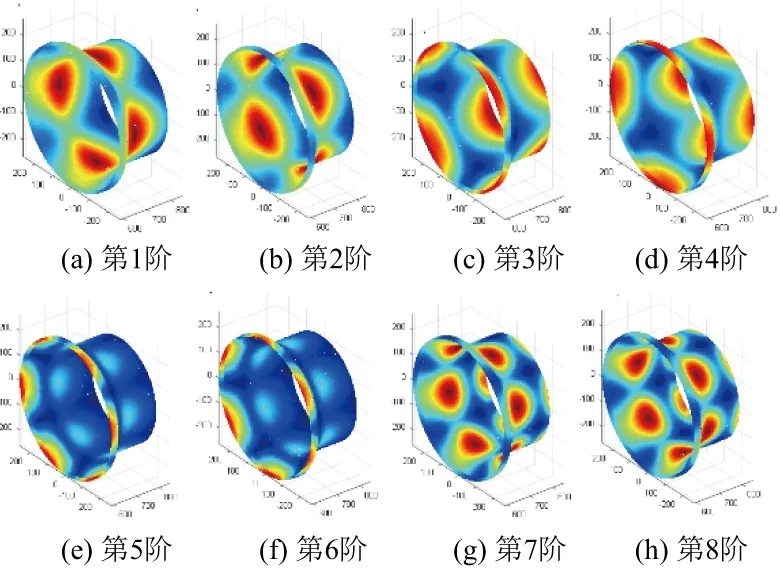
图4 前8阶模态重构振型图

2.2 RAT矩函数的去噪分析

在有限元模型的振型数据中加入正态分布的随机噪声，以达到一个模拟实际情况下噪声的效果。在此引入一个系数NIF(noise intensity factor)，表示正态分布的随机噪声的强度，NIF值为0.5代表强度为50%的随机噪声。再通过前文介绍的总体相似系数GSC来表示基于RAT矩去噪后的振型图像与原始振型图像的相似度，从而评价RAT矩函数的抗噪效果。在NIF值从0.1～1的情况下，分别计算出每一阶模态下加噪声的振型图像与原始振型图像的GSC均值与基于RAT矩去噪后振型图像与原始振型图像的GSC均值，将两条GSC随NIF值变化曲线绘制在同一张图中，见图5。

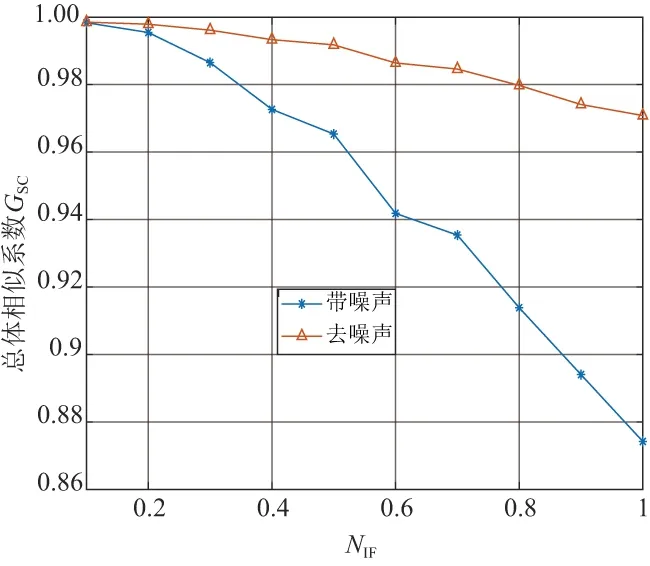
图5 不同噪声强度下去噪前后的GSC值

从图中可见，随着加入的噪声强度越来越大，带噪声的振型图像与原始图像的差别越来越大(GSC值越来越小)，当NIF为1也就是加入100%强度噪声时，带噪声的振型图像与原始图像的GSC降低到了0.87。而基于RAT矩去噪后的振型图像与原始图像的相似度虽然也随着NIF值的增大而减小，但是减小的速率非常小，能保持一个稳定性。即使噪声强度NIF为1的情况，去噪后振型图像的相似度GSC也在0.97以上，可以证明RAT矩函数能很好地应用在去噪过程中。

再将NIF为1情况下每一阶模态下带噪声与去噪声振型图像与原始图像的GSC值进行对比，对比图见图6。

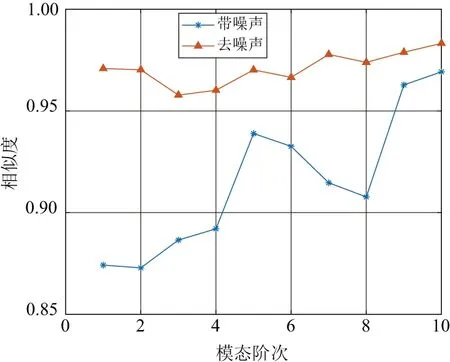
图6 NIF为1时各阶模态去噪前后振型图的GSC

可以看到，当噪声强度为100%时，使用RAT矩去噪后振型图像的相似度始终保持在0.95以上，这也在此验证了RAT矩函数的去噪能力，即使在噪声比较大的情况下，依旧能保证去噪后振型图与原始振型图有很高的相似度。

最后以第8阶模态的振型图像为例，在NIF值为0.2、0.5、1的情况下，列出第8阶模态的原始振型图、加噪振型图与去噪后的振型图对比。NIF为0.2、0.5和1时振型图像对比见图7。

由图7可以看到, 噪声强度系数NIF值为0.2时去噪后的振型图和原始振型图无太大差别，去噪效果十分显著，NIF值为0.5时去噪后振型图与原始图像的相似度相比于NIF为0.2的情况要低一些，但通过振型图像对比可以看到去噪效果依旧很好。当NIF值为1时，可以看到去噪后的振型图像与原始振型图像的相似度有所降低，但是仍具有良好的去噪效果。

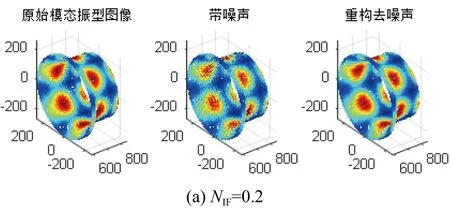
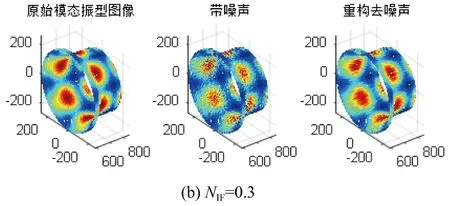
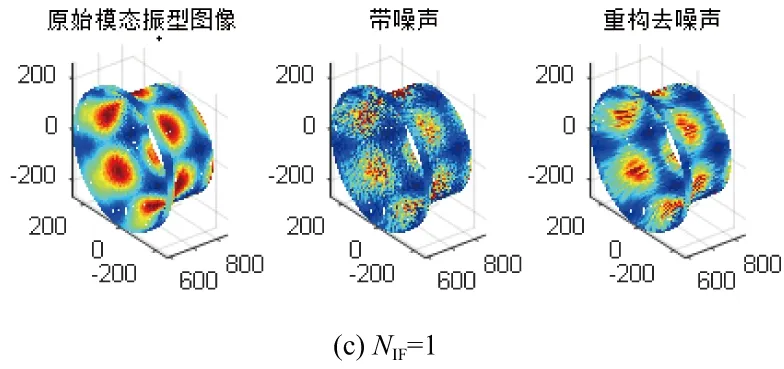
图7 不同噪声强度下第8阶模态去噪效果图

3 结语

本文研究了RAT矩函数对三维曲面结构的模态振型描述能力,并且进一步研究了RAT矩函数的去噪效果,得到以下结论：

1) 证明了使用RAT矩函数能够精确地描述三维曲面结构的模态振型,对进一步将RAT矩用于三维曲面结构的模型修正有重要的意义。

2) 验证了RAT矩函数的去噪能力,结果显示在各个噪声强度下利用RAT矩函数重构模态振型的去噪效果都十分明显,若将其应用在工程中能有效地解决试验过程中噪声影响的问题,具有一定的工程意义。