基于SVPWM及ADRC算法的无刷电机转矩脉动抑制控制系统研究
曹 萱, 关文卿, 罗 蕊
(兰州万里航空机电有限责任公司,甘肃 兰州 730070)
无刷电机具有体积小、重量轻、惯性小、效率高等优点,被广泛应用于工业控制、机器人、航空航天等领域[1]。在航空领域,随着人们对于飞机作动器的控制精度及抗干扰能力的要求愈来愈高,无刷电机的转矩脉动造成的振动、噪声以及对驱动功率管乃至整个作动器系统可靠性的影响越来越大。因此,避免无刷电机转矩脉动对整个作动器系统的影响是EMA系统必不可少的研究内容。
1 国内外发展现状
随着航空工业的发展,高性能、高精度的飞行是未来飞机运行的必然趋势,作为EMA的执行部件,稳定、可靠、精确的运行性能和快速实时响应的控制是无刷电机应用的必然要求。抑制电机运行中的转矩脉动,也是保护功率器件、提高电机运行性能的研究重点之一。
在国外,Sumega等[2]重点介绍了由于电机构造及控制造成的转矩脉动,说明了定子槽产生的齿槽转矩、反电动势与相电流波形的结合(控制)、磁阻转矩以及机械故障和电气故障是无刷直流电机产生转矩脉动的主要原因,但是没有介绍抑制转矩脉动的方法。Mohanraj等[3]基于逆变器输出电流的上升和下降的相等速率,引入了一种新的网络拓扑结构,该拓扑结构使用各种转换器来控制DC链路电压,以最小化BLDC电机驱动系统中的转矩脉动。Kim等[4]提出了一种减小换向转矩脉动的补偿算法,并通过实验验证,证明了使用该算法对BLDC电动机的转矩脉动抑制的有效性,该算法的主要思想是使换向期间两个换相的相电流的失配时间相等,即低速运行时减慢运行相的相电流的上升时间和高速运行时减慢断开相电流的下降时间相等,但是这一算法的运行需要精准的时间把控,实际应用并不容易。Senthilnathan等[5]使用了基于输出相电流迟滞控制(OCDHC)来抑制无刷电机的转矩脉动,并通过基于FPGA的仿真实验,验证控制方法的有效性,但是这一过程需要获得电机传导期(Conduction Period,CNP)精确的电流反馈。Gopinath等[6]提出了一种方法,并设计了BLDC电机驱动器的四象限运行仿真模型并减少了转矩脉动,该仿真模型可以有效地监视和分析速度、扭矩、反电动势的特征,借助模型预测控制器(Model Predictive Controller,MPC),可以在所有4个象限中控制电动机,而不会损失任何功率,但并未给出模型参数的计算方法。Lad等[7]在转矩脉动和逆变器损耗之间取得平衡,提出了一种新颖的具有12个电压空间矢量和重叠角控制的直接转矩控制,并进行了仿真和实验,但该方法需要大量的实验数据累积,通过查表的方式得到最佳重叠角。
国内,王淑红等[8]对电枢反应引起的转矩脉动进行了详尽的分析,从换相控制和磁路设计两大方面提出了一致方法。林平等[9]深入研究并提出了利用转矩观测器来检测测量转矩的方案,将相电流、电机转速及相电势作为输入信号,输出信号为转矩,构成转矩观测器,实现实时估算转矩的变化情况和大小,并针对不同情况下的转矩脉动情况进行了相应的补偿,控制实时性强,但这一方法计算复杂,工程实现有待验证。王正仕等[10]为了分析直流无刷电机运行时脉冲宽度调制方法对电机换相转矩的影响,在理论上从直流无刷电机方程入手,推导了直流无刷电机换相时的电磁转矩大小,分析了产生换相转矩的原因;针对使用传统脉冲宽度调制方法时电机转矩脉动较大的缺点,提出了一种新的脉冲宽度调制方法PWM-ON脉冲宽度调制,并从理论上证明了在直流无刷电机控制中,所提出的PWM-ON脉冲宽度调制方法产生的转矩脉动较小。王维强等[11]提出了内模控制与模糊控制相结合的驱动方式,在内模控制与双闭环控制相结合的基础上加入了模糊控制,电流环采用内模PI控制,转速环采用内模PI与模糊的共同控制;试验结果表明:基于模糊-内模控制的驱动系统在响应速度、超调量、转矩波动等性能方面与传统双闭环控制系统相比都有明显优势。
从近年来国内外研究现状可以看出,转矩脉动是危害功率器件、降低电机运行性能,甚至造成电机控制系统工作异常的因素之一,因此针对其相关内容进行研究是非常有必要的。
2 SVPWM算法及ADRC算法介绍
2.1 SVPWM算法
采用方波驱动的无刷电机,转矩脉动大,会产生较大的噪声及振动,甚至还会对整个驱动功率管乃至整个电机控制系统产生极大的不良影响,在电机低速运转时影响更为明显。SVPWM技术通过对逆变器各桥臂开关控制信号的不同组合,使逆变器的输出电压空间矢量的运行轨迹尽可能接近圆形,与SPWM调制技术相比,其逆变电路的电流输出波形的谐波成分更小,对直流母线的电压利用率也高出15%左右,更加适用于电机控制。在SVPWM控制算法下,电机的转矩更加平稳,脉动减少,其旋转磁场更加逼近于圆形,并且在现代数字化控制的背景下,容易通过单片机、DSP等控制芯片实现。
PWM逆变器的拓扑结构和等效开关模型如图1、图2所示。
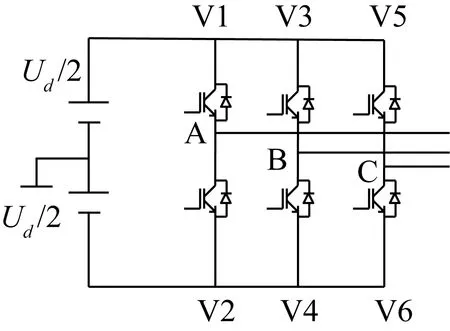
图1 逆变器拓扑结构
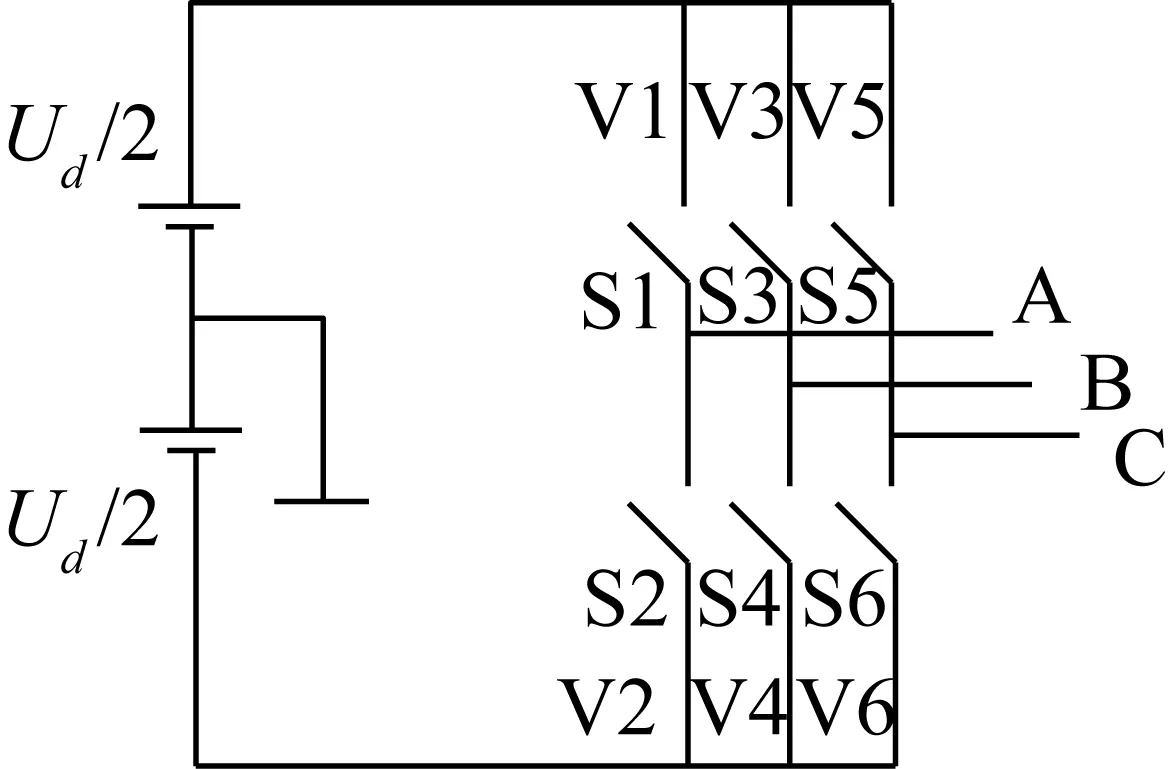
图2 等效开关模型
SVPWM通过控制6个功率管的开关状态,控制三相电压空间矢量的合成,从而逼近理想圆形磁链。用SA、SB、SC分别标记3个桥臂的状态,规定当上桥臂器件导通时桥臂状态为1,下桥臂导通时桥臂状态为0,当3个桥臂的功率开关管变化时,就会得到8种开关模式,其中有6个非零电压矢量,分别为U1=(001),U2=(010),U3=(011),U4=(100),U5=(101),U6=(110),两个零矢量为U0=(000),U7=(111),每种开关模式对应一个电压矢量,矢量的幅值为2/3Ud。有两种开关模式对应的电压矢量幅值为零,称为零矢量。
在某一时刻,设V1,V2,V3管处于开通状态,即Sa=Sb=1,Sc=0,设为三相对称负载,各开关管的开通电阻均相等,则逆变器的等效电路如图3所示。
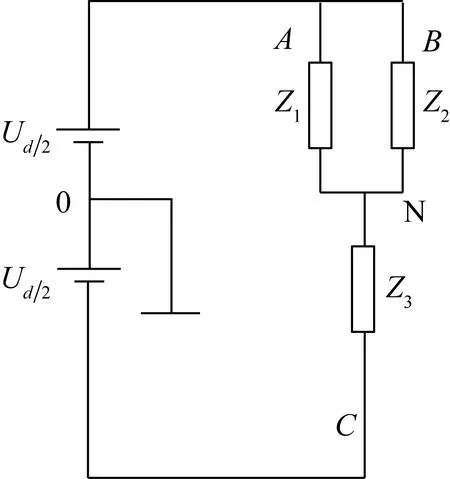
图3 Sa=Sb=1,Sc=0时逆变器的等效电路图
(1)
根据方程组(1)可得到该瞬时时刻的相电压为
(2)
将其在静止坐标系中表示出来,如图4所示。
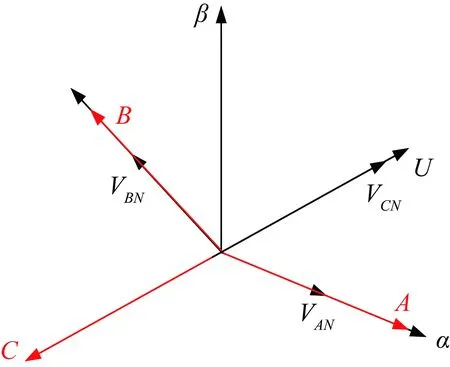
图4 α、β坐标系下电压矢量图
图4中,U是合成的电压矢量,在两相静止坐标系(α、β坐标系)下,利用相电压合成电压矢量U的表达式为
(3)
式中,k为三相静止坐标系向两相静止坐标系转换的变换系数,变换分为基于等功率的坐标变换和基于等量的坐标变换,这里选择等量的坐标变换,则k=2/3,则有:
(4)
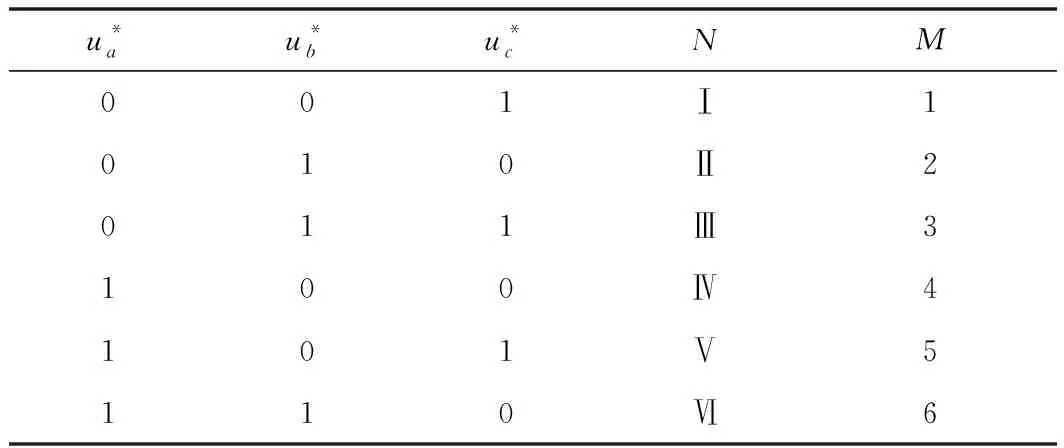
这样就得到了Sa=Sb=1,Sc=0开关状态下的电压矢量,按照同样的方法分析另外7种开关状态,可以分别得到每种开关状态所对应的电压矢量如表1所示。
图5为8个基本空间电压矢量,显然,仅靠这8个基本空间电压矢量是无法形成圆形旋转磁场的,因此必须引入多个中间矢量以逼近圆形电压矢量。
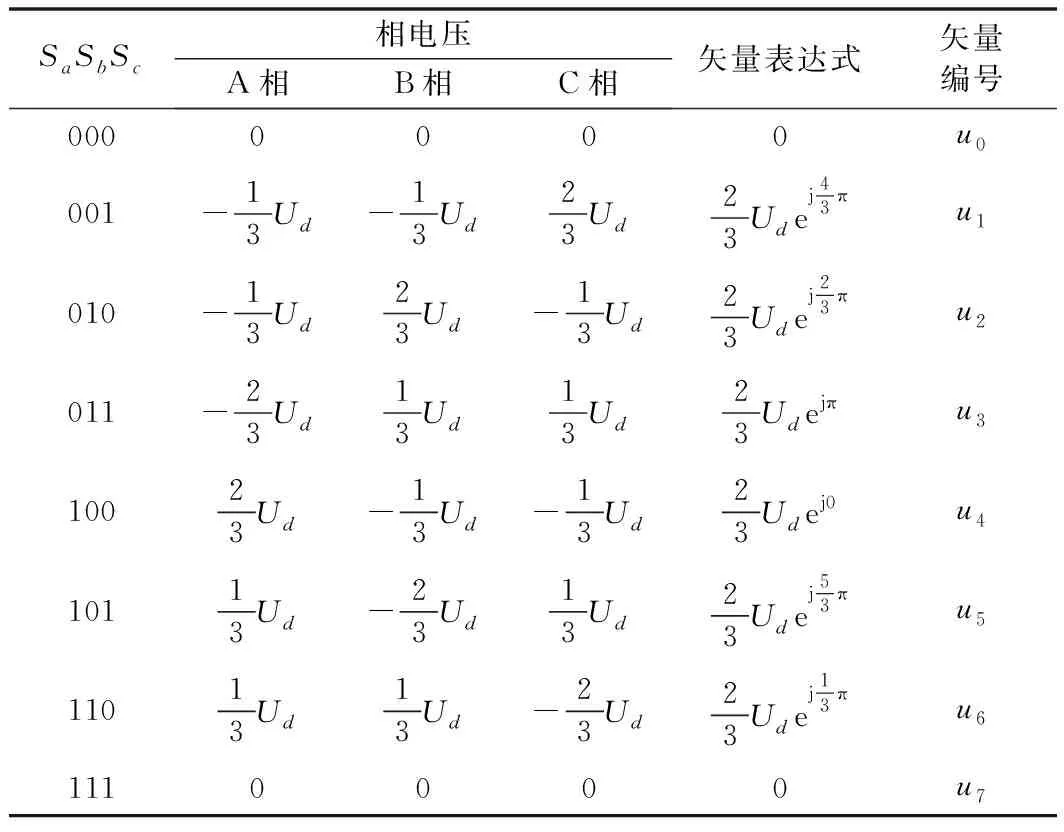
表1 不同开关状态对应的空间矢量表
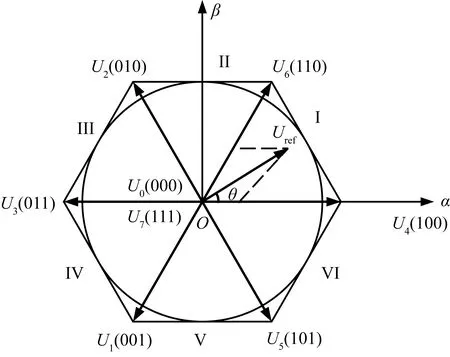
图5 基本空间矢量图
通过利用空间电压矢量合成技术,从基本电压矢量U4(100)位置开始,逆时针旋转,每个采样周期电压矢量旋转增加一个角度,利用每个扇区内相邻的两个基本非零电压矢量和零电压矢量合成。这样旋转一周后,就在空间电压矢量平面上近似等效形成一个平滑旋转的空间电压矢量,如图5所示的圆形轨迹。旋转的空间电压矢量投影于三相静止坐标系上,就为三相正弦波电压,便可实现SVPWM的目的,实现对电机三相电流的控制。
2.2 自抗扰ADRC算法
自抗扰控制技术是一种能够改善PID控制算法的非线性控制理论,该算法在PID的基础上,引入了“安排过渡过程”和同时合理“提取微分信号”的方法,并加入了扩张状态观测器对系统的未知模型和外部扰动总和作用量进行实时估计和补偿,从而改善控制器的性能[12]。
自抗扰控制器主要由以下3个部分构成:跟踪微分器(Tracking Differentiator,TD)、扩张状态观测器(Extended State Observer,ESO) 和非线性状态误差反馈控制律(Nonlinear States Error Feedback,NLSEF)[13]。
2.2.1 跟踪微分器原理
对于给定的输入信号v(t),TD将输出x1(t),x2(t)两个信号,如图6所示,其中x1(t)为跟踪v(t)的光滑可微信号,即安排适当的过渡过程;x2(t)为x1(t)的微分信号。

图6 跟踪微分器
假设二阶被控对象为式(5),其中w(t)为系统扰动。
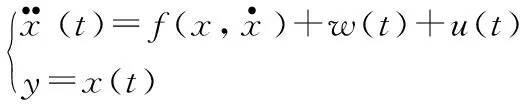
(5)
TD滤波器在实现时通常采用式(6)所示的离散化跟踪微分器:
(6)
式中,x1为跟踪输入信号v(k)的输出;x2为x1的导数;fst(·)为非线性函数,表示为
(7)
式中,h为积分步长;α为非线性因子;h0为TD的滤波因子,h0越大滤波效果更好,但跟踪信号的相位损失越大;r为速度因子,即r越大跟踪速度越快,但噪声也越大。当h>h1时,对于含有噪声的信号,TD滤波器有较好的滤波功能,此时输出x1即为输入信号v(t)滤波后的信号。大量仿真实验证明,离散TD能够快速、无超调、无震颤地跟踪输入信号,且能给出较好的微分信号。
2.2.2 扩张观测器原理
ESO是一种通过对不确定转改对象的观测器形式的跟踪微分器进行改造而获得的状态观测器[14]。通过将ESO观测出的对象模型的内、外扰动的实时作用量补偿到控制中,可将不确定非线性系统动态地转化为积分器串联型结构系统。对于二阶被控对象:
(8)
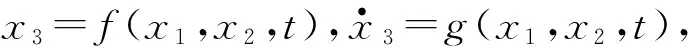
(9)
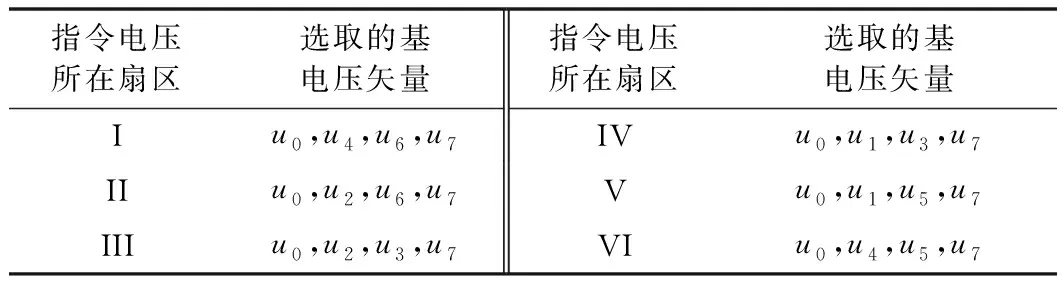
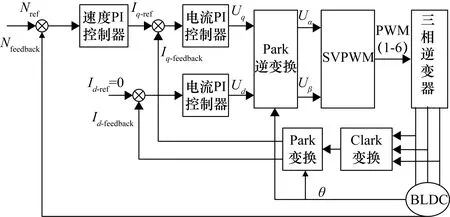
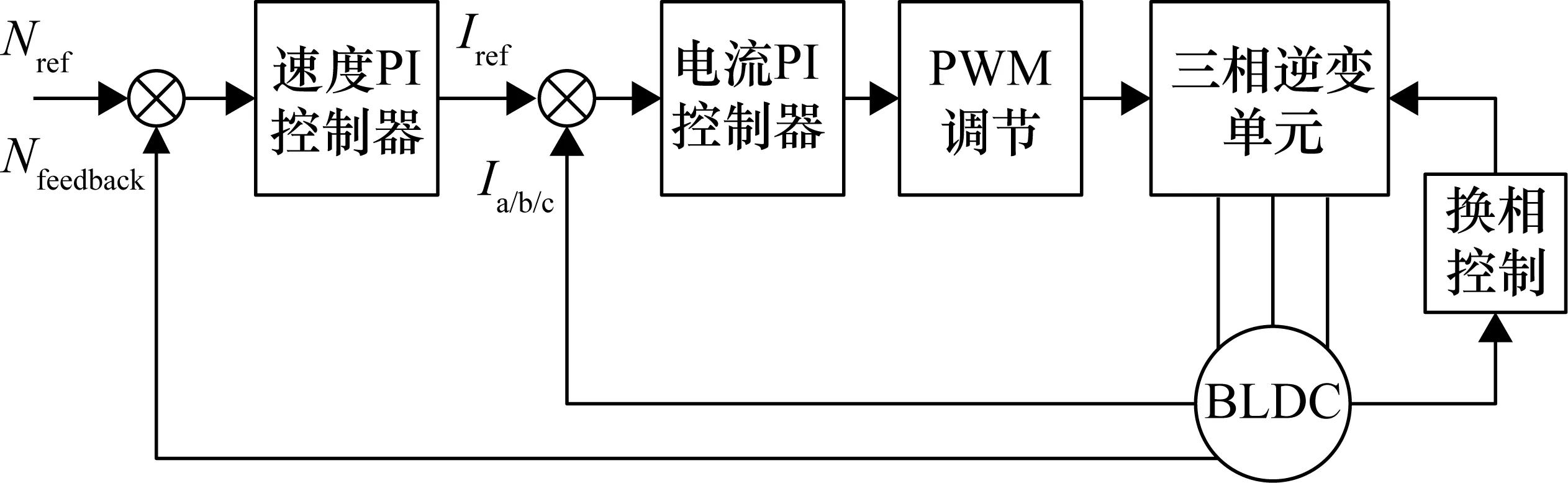
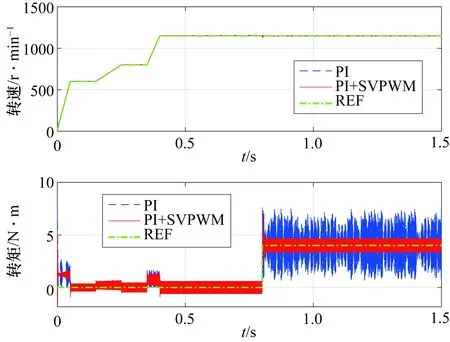
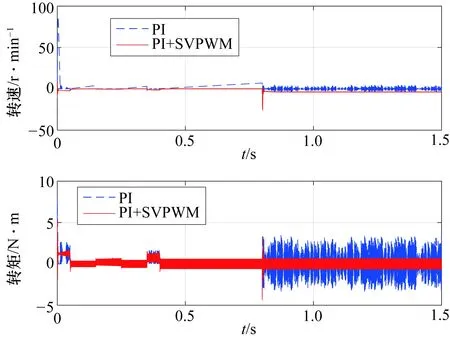
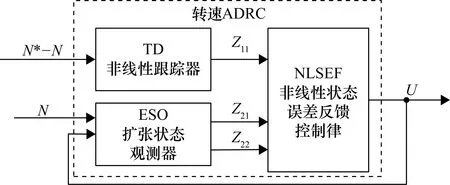
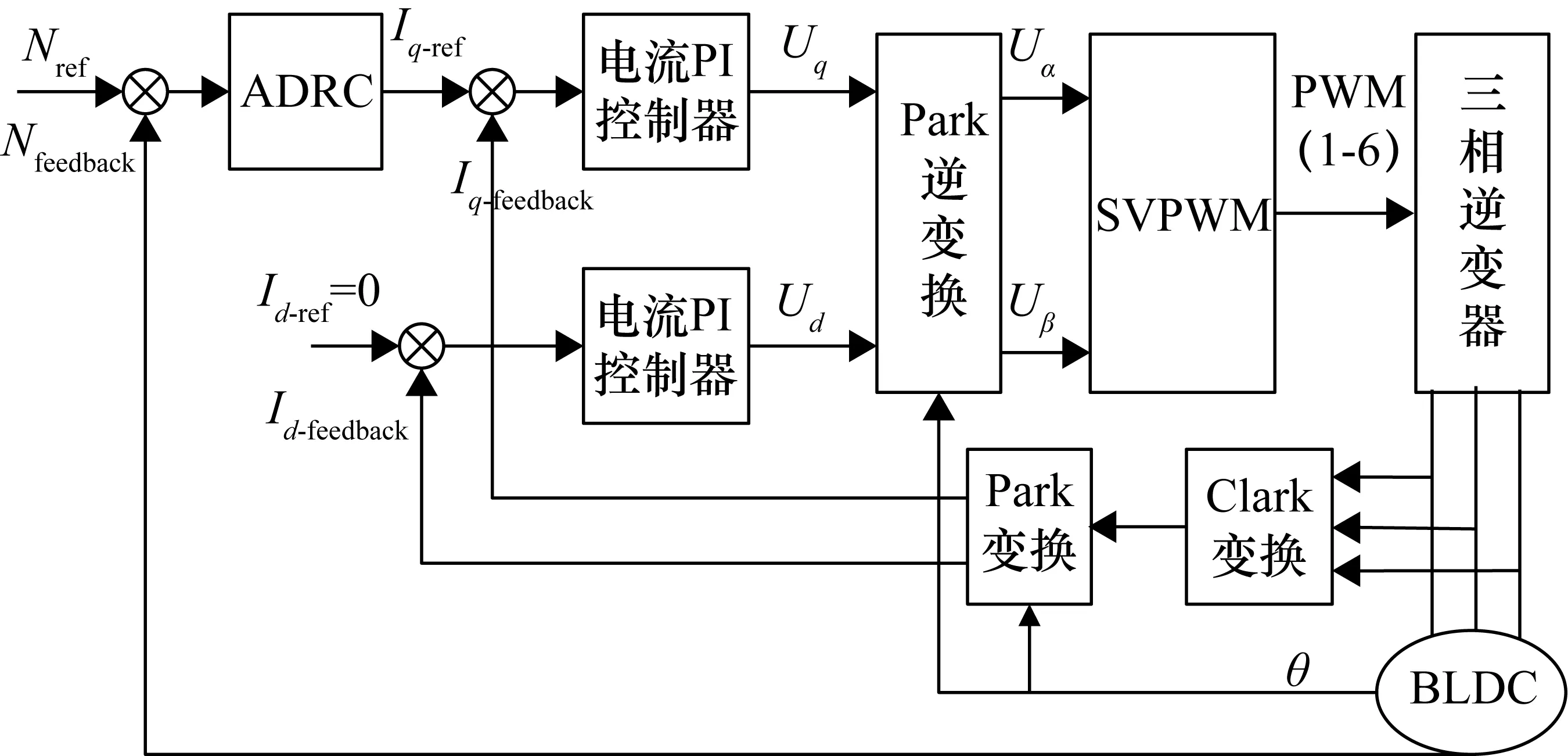
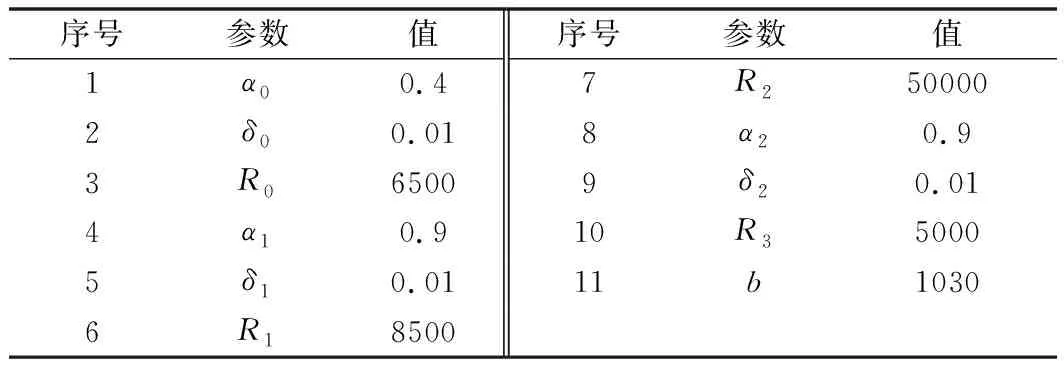
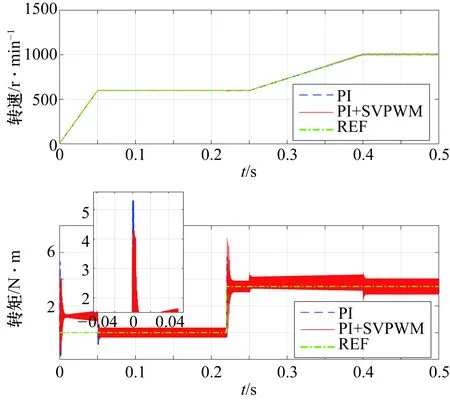
式中,a2 式(9)称为式(8)的扩张状态观测器。离散化状态观测器见式(10)。 (10) 式中,e(k)=z1(k)-y(k),且 式中,z1(t),z2(t)为状态变量的估计值;z3(t)为估计对象的所有不确定模型和外部扰动的实时作用和;β01,β02,β03为可调参数;δ为滤波因子,该参数越大,滤波效果越好,一般地,δ取值为5T≤δ≤10T。 2.2.3 非线性状态误差反馈控制律原理 非线性状态误差反馈控制律采用了一种独立于对象模型的非线性控制器结构。系统的控制律为u=u0-zn+1/b,即通过扩张状态观测器将含有位置扰动的非线性不确定性对象划为积分串联型对象,这样就能用状态误差反馈来设计理想的控制器,控制律的选择可采用非线性配置,即可采用非线性状态误差控制律——NLSEF[15],数学表达式为 (11) 式中,xi-zi为安排过渡过程及其各阶倒数和对象的状态变量之间的差。非线性状态误差反馈控制律NLSEF的离散算法为 (12) 式中,x1为安排的过渡过程,x2为该过渡过程的一阶导数,x1,x2为TD的输出。ESO的输出z1,z2,z3为对象的状态变量。TD、ESO输出端两组变量的误差为e1=x1-z1,e2=x2-z2,为对象跟踪参考输入v(t)时的状态误差。 系统的“内部扰动”(将系统模型视为系统的“内部扰动”)和“外部扰动”综合为整个系统的“扰动”。NLSEF自动检测系统“扰动”,并给予补偿分量,若ESO的速度足够快,那么这个补偿分量就能精确地反映出系统的扰动情况。被控对象被化为“积分器串联型”后,就可构造出理想控制器,这完全归功于该分量的补偿作用。补偿分量作用的实质是一种“抗扰”作用。 6个长度不为零的矢量将一个周期分成了6个扇区,为了减少管子的开关次数以及增加系统的稳定性,合成目标矢量采用其所在扇区最近两个基本矢量和两个零矢量共同合成。例如当电压矢量指令u*出现在第I扇区时,应当用u0,u4,u6,u7来合成中间电压矢量以追踪电压指令。基本矢量选择表如表2所示。 表2 基本矢量选择表 表3 扇区判断表 (13) 在判定了指令电压矢量u*所在的扇区和所需要的基电压矢量后,接着计算两空间矢量的作用时间。根据一个开关周期T*内“合成分矢量分别作用时间T1,T2之和等于T*”、“合成分矢量与作用时间乘积之和等于u*”可得u*在各个扇区的作用时间T1,T2如表4所示。 表4 各个扇区中T1,T2对应关系表 其中,X,Y,Z的值为 (14) 基于SVPWM及传统PI算法的系统框图分别如图7、图8所示,包括速度环PI调节模块、电流环PI调节模块、坐标变换模块、SVPWM模块、无刷直流电机模型和信号检测模块等。 图7 基于SVPWM算法的控制系统 图8 经典电流转速双闭环控制系统 图9为分别为采用传统PI控制算法、PI+SVPWM算法、期望值对比的转速及转矩图,从图9中可以直观地看出,基于SVPWM算法的无刷电机控制器的转速及转矩的波动相对更小。图10为两种算法下的误差,相比于传统PI控制,基于SVPWM算法的无刷电机控制器不仅在电机启动时产生更小的波动,在整个控制过程中,跟踪转矩期望值也具有更好的效果。 图9 转速及转矩响应 图10 转速及转矩的误差对比 为了设计自抗扰系统,将无刷直流电机视为一个二阶非线性系统。 (15) 结合二级对象离散化方程(15),本控制系统中的转速自抗扰跟踪微分器的公式为 (16) 式中,v为给定信号;z11为跟踪给定信号的TD的输出信号;R0为决定跟踪快慢的参数;fal为抑制误差的非线性函数: (17) 式中,e为输入误差;α为反映增益变化率的参数,当0<α<1时,α越大,增益的变化速率随误差的增大而越快;δ为避免函数在原点振动的较小参数,决定函数增益线性变化的区间大小。 本控制系统中的扩张状态观测器的公式为 (18) 式中,z11为跟踪给定信号的TD的输出信号;z21为状态变量的估计值;z22为所有不确定模型和外部扰动的总作用量;y为实际测量值;δ1为滤波因子;R1,R2为扩张状态观测器针对系统的可调参数。 本控制系统中的非线性状态误差反馈控制律的公式为 (19) 转速ADRC的结构如图11所示,基于转速ADRC无刷电机转矩脉动抑制器的架构如图12所示。 图11 转速ADRC结构 图12 基于转速ADRC无刷电机转矩脉动抑制器设计 基于以上架构,控制器中的转速ADRC的相关参数选择见表5。 表5 转速ADRC的参数表 基于以上架构及参数设置,仿真结果如图13、图14所示。图13中二者转速响应对比并不明显,但通过图14中转速误差的对比即可看出,增加了ADRC算法的控制器误差更接近于0,即转速响应更好;图13中可以明显地看出仿真初始阶段,增加了ADRC算法的转矩响应超调更小,通过图14的转矩误差对比可看出给定转矩变化时,ADRC算法可以更加有效地抑制转矩的脉动。 图13 仿真结果对比 图14 仿真误差对比 本文开展了针对无刷电机运行中转矩脉动抑制的控制系统建模与仿真,从仿真波形可以看出,相比传统PI控制系统,基于SVPWM及ADRC算法的控制系统可以很好地降低无刷电机运行中的转矩脉动,从而降低对功率器件的影响,使电机更加可靠、稳定地运行。3 无刷直流电机转矩脉动抑制器建模与仿真
3.1 基于SVPWM算法的无刷电机转矩脉动抑制器建模与仿真
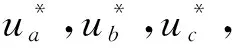
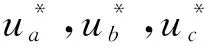
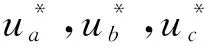

3.2 基于ADRC算法的无刷电机转矩脉动抑制器建模与仿真

4 结束语

