输电线路工程地锚受力计算修正

单 军，郑亚平

（1.山东送变电工程有限公司，山东 济南 250118；2.济南鲁源电气集团有限公司，山东 济南 250012）

0 引言

施工地锚在送电线路施工中主要用于组塔、架线过程中的地面锚线作业，它体积小、重量轻，在保证埋深的前提下承载力大，是施工中不可替代的受力工器具之一，其抗拔力计算正确与否直接影响线路施工安全。在高压送电线路工程的施工指导手册中［1］，地锚抗拔力（承载力）的计算源自土力学的土重法。由于地锚拉线与地面不垂直，施工指导手册在对地锚抗拔力使用土重法计算的理解上存在偏差。通过对经典公式及配图进行分析，对经典公式进行修正，使地锚抗拔力的计算结果更加准确，保障地锚的施工安全。

1 经典公式分析

1.1 经典公式概述

依据《高压架空输电线路施工技术手册》，地锚的极限抗拔力是根据地锚受力后达到极限平衡状态时，在其受力方向上土壤沿抗拔角方向形成剪裂面后带动的倒截锥体土块重量来计算［2］，见式（1）。按地锚带动一斜向倒截锥体土块考虑，地锚抗拔力分析如图1 所示。

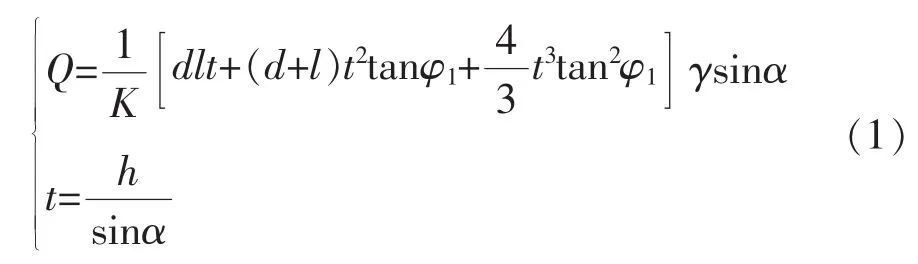
式中：Q 为地锚容许抗拔力，kg；φ1为土壤的计算抗拔角，°，粉砂φ1=22°，细砂φ1=26°，中砂、粗砂φ1=28°，稍密粉土φ1=10°～15°，中密粉土φ1=20°；密实粉土φ1=25°，软塑黏土φ1=10°，可塑黏土φ1=20°，硬塑、坚硬黏土φ1=25°；d 为地锚宽度，m；l 为地锚长度，m；h 为地锚顶面距地面埋深，m；γ 为土壤单位容重，kN／m3，粉砂γ=15 kN／m3，细砂γ=16 kN／m3，中砂、粗砂γ=17kN／m3，稍密粉土γ=15 kN／m3，中密粉土γ=16 kN／m3，密实粉土γ=17 kN／m3，软塑黏土γ=15 kN／m3，可塑黏土γ=16 kN／m3，硬塑、坚硬黏土γ=17 kN／m3；K 为抗拔安全系数，取2～2.5；t 为土中斜向长度，m；α 为地锚受力方向与水平方向的夹角，°。

图1 地锚抗拔力分析

1.2 理论分析

式（1）被称为经典公式，其作为输电线路工程组塔架线施工中地锚应力计算校核的重要公式，自20世纪70 年代一直延续至今，已在电网建设领域得到普遍应用，但仍存在一些问题。

经典公式中地锚抗拔力的概念与土力学的概念并不一致。经典公式表述的地锚抗拔力是指地锚受力方向沿拉线方向斜向上，与抗拔角倾斜方向一致；而在土力学和配电线路（高级工）教材［3］中均是指地锚受外力垂直向上的分力作用时，抵抗向上滑动的能力。依据经典公式理论，地锚的极限抗拔力是根据地锚受力后达到极限平衡状态时，在其受力方向上土壤沿抗拔角方向形成剪裂面后带动的倒截锥体土块重量来计算，即图1 中沿着外侧抗拔角虚线以内的土块重量。假设抗拔角φ1与地锚受力夹角α 相等，则一侧地锚抗拔角与地面相交，另一侧地锚抗拔角与地面平行无法相交，即包含在抗拔角内的土块体积无限大，显然这是不可能的。

经典公式理论表述的地锚抗拔力等于在其受力方向上土壤沿抗拔角方向形成剪裂面后带动的倒截锥体土块重量。但土的重力方向竖直向下，而抗拔力方向沿拉线方向斜向上，二者方向不一致，故不能直接对等。但如果按照土力学理论，地锚抗拔力是地锚斜拉力的垂直分量，竖直向上，则不存在不能直接对等的问题。

1.3 公式分析

经典公式通过转换可以变为式（2）的形式。

式中：V 为计算土体积，m3。

由式（2）可知，体积公式可以看作棱台由1 个棱柱、4 个楔形体和4 个棱锥组成，其中4 个棱锥体积相等，可知经典公式依据左右对称的棱台计算，这与公式理论不一致。若依据经典公式理论，土的体积为受力方向上土壤沿抗拔角方向形成剪裂面后带动的倒截锥体土体积，如图2 所示，可将所计算土的下平面近似看作通过中心点与地面平行的平面，则该土体积可以用棱台体积通用公式倒推得到式（3）。

式中：d1为计算土体上表面宽度，m；l1为计算土体上表面长度，m。

图2 所计算土的体积

由式（3）与式（1）对比可以看出原经典公式并不是受力方向上土壤沿抗拔角方向形成剪裂面后带动的倒截锥体土体积，且式（3）可以得出当α=φ1时，cot（α-φ1）无限大，进而得出V 无限大，这与理论分析结果一致。

由经典公式原理及经典公式本身分析得到，原经典公式在概念上存在误解，不能够准确反映抗拔力；虽然其计算相对简单，但与实际土重法计算存在偏差。

2 土重法计算

根据土力学中基础抗拔力的概念，采用土重法对地锚抗拔力重新进行计算。地锚抗拔力依据土力学知识定义为地锚受外力垂直向上的分力，即抵抗向上滑动的能力［4］。依据DL／T 5219—2005《架空送电线路基础设计技术规定》，采用土重法计算抗拔力时，存在临界深度hc。不超过临界深度计算土重时，存在抗拔角使土体积增加至抗拔角范围以内，可看作深度为h、下平面与地面平行的棱台；超过临界深度计算土重时，应分为临界深度以上含抗拔角土重和临界深度以下无抗拔角土重两个部分之和［5］，如图3 和图4 所示。

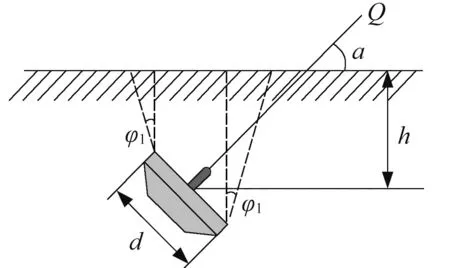
图3 h≤hc 时地锚抗拔力

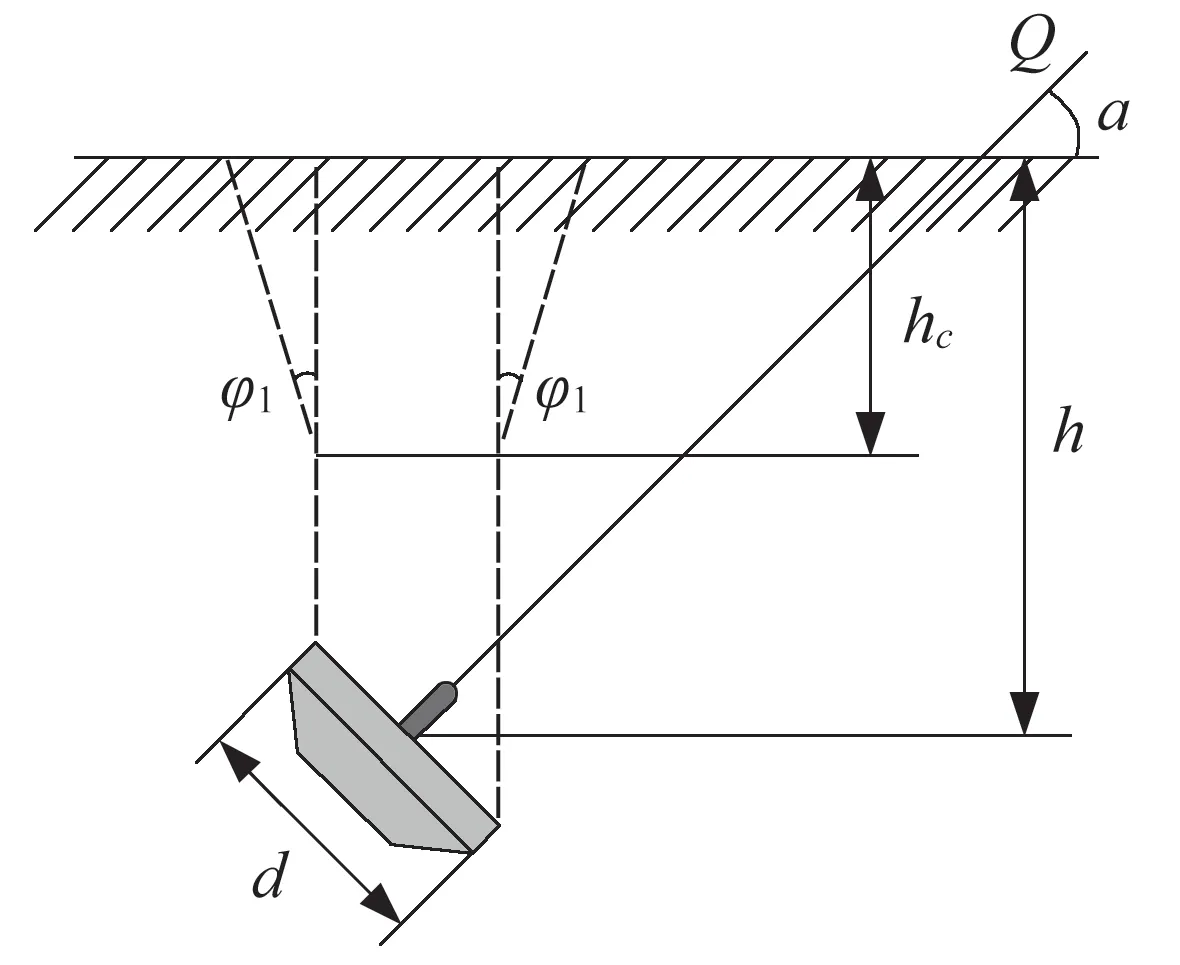
图4 h＞hc 时地锚抗拔力

当h≤hc时，地锚抗拔土壤体积为

当h>hc时，地锚抗拔土壤体积为

式中：k 为土质系数，稍密、密实砂类土k=3.0，坚硬、硬塑黏性土k=2.5，可塑黏性土k=2.0，软塑黏性土k=1.5［6］。

此时，图4 中Q 为地锚斜向上拉力，抗拔力只是Q 拉力的垂直分量，故地锚斜拉力的计算公式应为

按照式（6）可计算不同规格地锚在不同地质情况下的临界深度，详见表1。

在施工中，一般大号地锚埋深在距地面2.0～2.5 m 处，中号地锚埋深在距地面1.8～2.0 m 处，小号地锚埋深在距地面1.5～1.8 m 处。从表1 可以看出，在稍密、密实砂类土中，各类地锚临界深度数值较高，可以直接使用式（4）完成土体的计算，其结果与经典公式计算结果差距不大。随着土质逐渐变差，临界深度数值逐渐变小，至软塑黏性土所有规格地锚埋深值均大于临界埋深值，此时应使用式（5）完成土体计算，由于式（5）为部分埋深使用抗拔角计算土体，数值上会比经典公式小。经过计算，在软塑黏性土中埋设1.8 m 深的小号地锚采用修正后公式计算土体积为1.828 m3；采用原经典公式计算土体积为10.945 m3，经典公式计算结果是修正后公式计算结果的近6 倍。说明原经典公式增大了抗拔力的计算数值，且增大比例随地锚埋设深度增大而成倍增加。此时，经典公式计算结果已不能真实反映现场地锚实际抗拔力，会对地锚埋设安全产生错误判断，导致技术人员选择较小尺寸地锚，或认为同等尺寸地锚埋深相对浅就可以满足现场实际抗拔力要求，大大降低施工及线路运行的安全性。

表1 地锚土重法临界深度

3 结语

经过理论和公式分析可知，原地锚受力计算存在理论上和公式上的偏差。在土质较差、地锚埋设较深的情况下经典公式计算偏差较大，已严重影响对地锚抗拔力是否满足安全要求的判断。采用土重法对公式修正后更能准确计算地锚抗拔土壤体积，得到更加准确的抗拔力和斜拉力及符合抗拔安全要求的地锚埋深。通过输入地锚实际埋深，可计算出地锚可承受最大斜拉力与计算拉力进行比较，确定地锚受力是否安全。

需要注意的是，所述地锚埋深为地面至地锚上表面的深度，在实际开挖深度计算时需要在此基础上增加地锚高度。