地铁工程钢筋混凝土梁疲劳损伤演化和寿命预测模型研究

陈梦成, 温清清, 罗 睿, 谢 力

(1. 华东交通大学 土木建筑学院，江西 南昌 330013；2.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室， 江西 南昌 330013； 3. 华东交通大学 理学院，江西 南昌 330013)

采用直流供电牵引方式的地铁列车在运行时，部分电流泄漏到土壤中，会对主体结构造成腐蚀。地铁混凝土主体结构通常距地面较深，土壤透水性较强时，氯离子极易经混凝土渗透至钢筋表面，诱发钢筋腐蚀[1-4]。此外，地铁在运行过程中会对地铁钢筋混凝土结构施加带有周期性的循环荷载，通常称为疲劳荷载。多种因素协同作用，势必加剧结构的损伤劣化，给地下列车的安全运行造成极大威胁。多种不利因素协同作用时，地铁钢筋混凝土结构弯曲疲劳损伤劣化及寿命预测模型也更趋复杂[5]。因此，有必要对地铁钢筋混凝土腐蚀疲劳损伤预测模型进行深入研究。

关于钢筋混凝土疲劳损伤预测，已有很多学者做了相关方面的研究。Dang等[6]通过三点弯曲试验研究了长期处于氯离子环境中的钢筋混凝土服役寿命演化规律。Ma等[7]基于概率分析方法，提出了考虑各种影响因素来源不确定性的疲劳寿命预测。王海超等[8]以钢筋混凝土梁为研究对象，在空气环境、淡水环境和盐水环境中开展疲劳试验，对疲劳荷载下三种环境中梁的变形发展过程以及疲劳寿命进行研究。试验结果表明，疲劳往复荷载与环境共同作用下，钢筋混凝土梁的挠度-荷载循环次数曲线呈明显的三阶段特征。根据试验结果给出了三种环境下不同荷载循环次数时钢筋混凝土梁的挠度公式及S-N方程。吴瑾等[9]通过8根锈蚀钢筋混凝土梁弯曲疲劳试验，研究了疲劳荷载下锈蚀钢筋混凝土梁的破坏形态、变形性能、疲劳强度与寿命。李士彬等[10]通过钢筋混凝土梁疲劳试验，引入剩余刚度和损伤度概念，研究疲劳损伤对构件造成的刚度衰减规律，结果表明：工程应用中可以损伤度D为1作为失效判据，再依据少量循环的疲劳试验确定混凝土梁刚度衰减速率k的大小，预测钢筋混凝土梁的疲劳寿命。季家林等[11]通过对钢筋混凝土梁的连续超声波检测，选取有关数据建立了其损伤演化方程和内、外损伤变量之间的关系，并基于有限元分析建立了梁疲劳破坏的极限状态方程，最终运用以上关系分析了钢筋混凝土梁的剩余寿命。朱红兵等[12]通过疲劳试验观测，得出钢筋混凝土梁刚度退化呈现出非常明显的三阶段规律，刚度退化曲线显“S”形形态，并根据刚度退化规律拟合得到了钢筋混凝土梁刚度退化计算公式。陈梦成等[13-15]通过钢筋混凝土梁在空气环境、杂散电流环境、氯盐环境和两者耦合环境下的疲劳试验，研究了这4种环境下梁的变形发展过程、刚度损伤过程和电化学腐蚀参数。结果表明，在不同腐蚀疲劳环境作用下，梁挠度-循环比和刚度损伤变量曲线呈三阶段特征，其变化程度在空气环境最慢，氯盐环境到疲劳后期较快，杂散电流环境较快，耦合作用下最快。对于钢筋混凝土梁在杂散电流、氯离子和疲劳荷载三因素耦合协同作用下的疲劳损伤预测，目前仍缺乏深入、有效的研究。这显然无法适应当下中国城市轨道交通高速发展对地铁钢筋混凝土结构安全性和耐久性研究的要求。

本文拟通过试验测定钢筋混凝土试验梁跨中挠度，跟踪钢筋混凝土梁在腐蚀环境与疲劳荷载作用下的腐蚀疲劳损伤演化全过程。根据试验梁跨中挠度演化规律建立腐蚀环境下四点弯曲疲劳寿命和损伤累积预测模型，包括单因素变化下的疲劳寿命预测模型、累积损伤模型以及多因素耦合下的疲劳寿命预测模型。并使用这些模型对腐蚀环境下地铁钢筋混凝土梁寿命进行预测和评估，同时将预测值和试验值进行对比验证。

1 预测模型

在预测结构材料的服役寿命和损伤时，国内外专家一般采用剩余强度、剩余刚度作为主要参数，对构件的服役寿命及损伤情况进行描述[16-18]。受以上学者研究成果启发，本文拟对杂散电流、氯离子和弯曲疲劳荷载共同作用下钢筋混凝土梁的疲劳寿命和损伤建立半经验解析预测模型，并试图通过该预测模型对钢筋混凝土试验梁的疲劳寿命和损伤状态进行预测和评估。

1.1 挠度演化半经验解析模型

四点弯曲疲劳试验采用荷载控制。疲劳试验中变化参数应力水平取值为0.6、0.7、0.8，腐蚀环境杂散电流强度取值为10、20、30、40 V，氯离子浓度则取值为2.5%、3.5%、5%、10%(质量分数，以下同)。依据材料力学理论，钢筋混凝土试验梁的刚度退化与其挠度增加有关，因此，在疲劳试验中，可记录下钢筋混凝土试验梁跨中挠度d0max/dmax随疲劳荷载循环次数变化情况。d0max是指第1次疲劳荷载循环过程中的试验梁跨中最大挠度；dmax则为疲劳荷载循环过程中记录的试验梁跨中最大挠度。钢筋混凝土试验梁在腐蚀环境和疲劳荷载耦合下跨中挠度比值随疲劳循环次数增加的典型演化趋势见图1，图1中N为加载过程中的疲劳荷载循环次数，Nf为试验梁疲劳寿命对应的疲劳荷载循环次数。由图1可知，跨中挠度增长从初始加载到试验梁最终疲劳损伤破坏阶段，挠度演化经历了比较明显的3个阶段：①初始快速下降阶段。此阶段试验梁由于受到预腐蚀开裂的影响，在疲劳荷载加载初始阶段，其挠度快速增加，挠度比值则快速递减，该阶段对应的疲劳荷载循环次数很少；②稳定下降阶段。该阶段试验梁挠度逐渐增大，其增长速率逐渐趋于平缓，相应挠度比值则逐渐平缓递减，疲劳损伤累积逐渐增加，疲劳损伤与试验梁形状、尺寸、材料属性、腐蚀环境和荷载条件有关，情况极为复杂，此阶段末端对应的疲劳荷载循环次数为试验梁的疲劳寿命；③损伤破坏急剧下降阶段。此阶段试验梁挠度急剧增加，直至断裂破坏。该阶段内疲劳荷载循环次数极少。

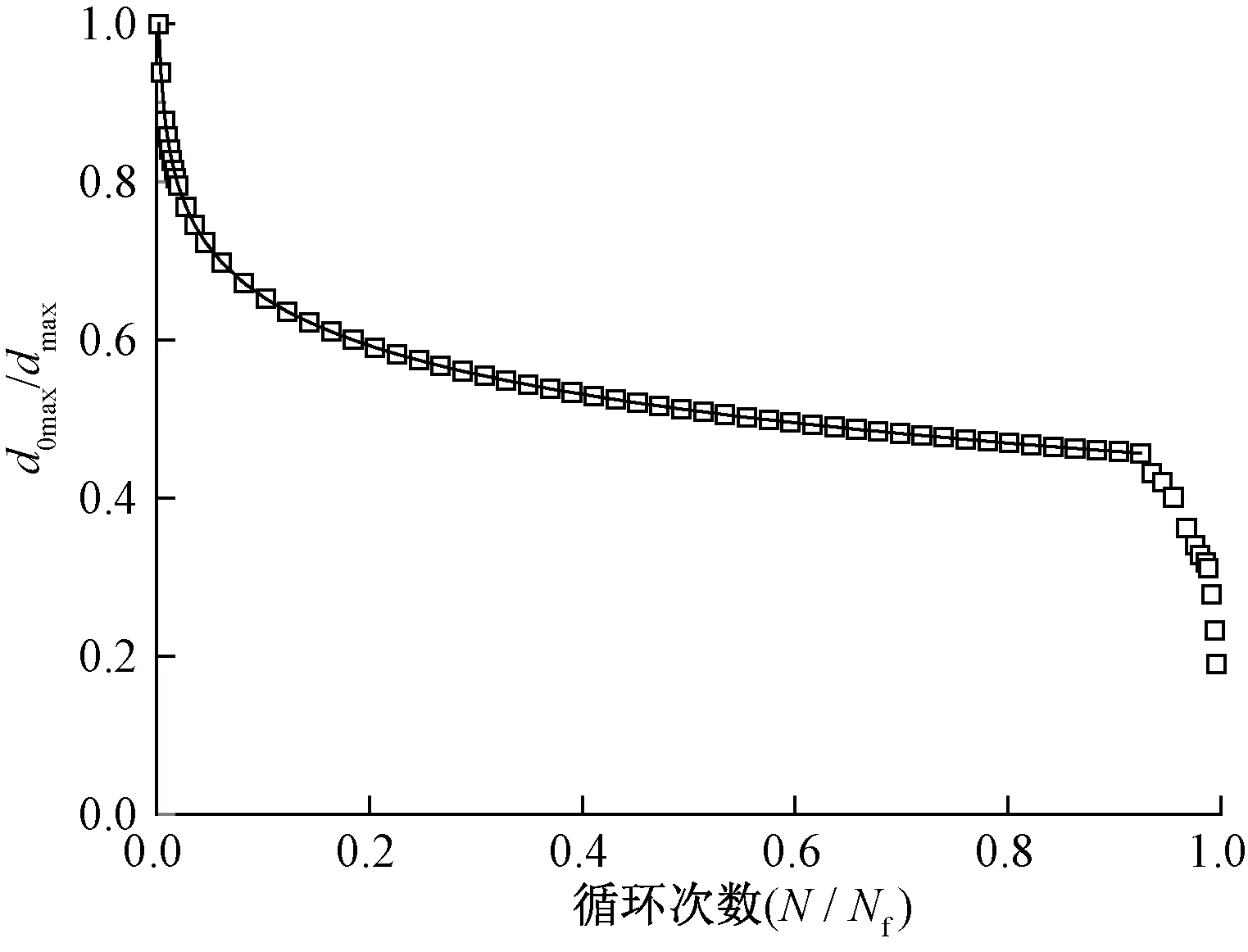
图1 腐蚀环境下钢筋混凝土试验梁挠度演化趋势

钢筋混凝土试验梁挠度增加导致其疲劳弯曲模量(亦称刚度)退化。试验结果表明钢筋混凝土试验梁挠度增加可以表示为疲劳荷载循环次数的对数函数(见图1)，其函数表达式为

(1)

式中：A为与试验初始条件有关的参数；B为与应力水平、腐蚀环境和材料属性相关的参数；Nif为疲劳试验过程中验梁跨中最大挠度dmax的初始记录所对应的循环次数，这主要是考虑到初始疲劳加载记录的不确定性和试验结果的分散性。

式(1)可以用来描绘试验梁跨中挠度演化的最初两个阶段，如图1中实线所示。考虑到钢筋混凝土试验梁跨中最大挠度dmax的初始记录所对应的循环次数Nif一般都很小，dmax和第1次循环中的d0max也相差不大，因此，为了解析上的便利，在疲劳试验分析中通常dmax的初始记录可近似视为d0max。据此，可以得到A=1，那么式(1)可以进一步改写为

(2)

另外，根据试验结果，可以假设式(2)中的模型参数B的变化遵循幂函数规律，即

B=b1rb2+b3

(3)

式中：系数b1、b2、b3与腐蚀环境、荷载条件与材料属性相关，可由试验数据和回归分析方法确定；r为应力水平。

将式(3)代入式(2)，可进一步得到试验梁跨中挠度的演化公式为

(4)

1.2 疲劳寿命预测模型

在荷载控制的疲劳试验中，定义钢筋混凝土梁刚度折减α时所对应的临界循环次数作为试验梁的疲劳寿命[11]，即

d0max=(1-α)dαmax

(5)

根据式(4)、式(5)，钢筋混凝土试验梁的疲劳寿命可以表示为

(6)

式中：β=1-α。

1.3 疲劳累积损伤预测模型

试验梁疲劳损伤累积到一定程度后，常常会发生疲劳损伤破坏断裂。由于本文试验是在杂散电流、氯离子腐蚀环境和疲劳载荷协同作用下进行的，加上混凝土材料具有各向异性特征，骨料之间也会出现脱粘现象，因此钢筋混凝土试验梁疲劳损伤机理极为复杂。为了度量钢筋混凝土试验梁在某一时刻所达到的损伤程度，根据损伤力学理论，通常将其所有损伤用一个损伤变量D来描述，它与试验结果有关。通常假定疲劳荷载循环开始时名义损伤变量DF为零，试验梁发生疲劳损伤破坏时名义损伤变量DF为1，其数学表达式为

(7)

对于控制荷载的疲劳试验而言，可以用钢筋混凝土试验梁的跨中挠度变化来描述其疲劳损伤演化，即损伤变量DF可以表示为

(8)

式中：dαmax为刚度折减α时对应的试件跨中位移最大值。

将式(4)、式(5)和式(6)代入式(8)，得到钢筋混凝土试验梁的疲劳损伤演化方程为

(9)

2 腐蚀环境下疲劳试验

2.1 试验梁设计

试验梁采用强度等级为C40的混凝土，设计配合比为水泥∶砂∶石子∶水=1∶1.35∶2.51∶0.35，坍落度为150 mm。水泥为P·O42.5级普通硅酸盐水泥，砂为赣江江砂，石子最大粒径为25 mm，采用自来水拌合。混凝土28 d立方体抗压强度为42.67 MPa。

表1 试验用钢筋力学性能

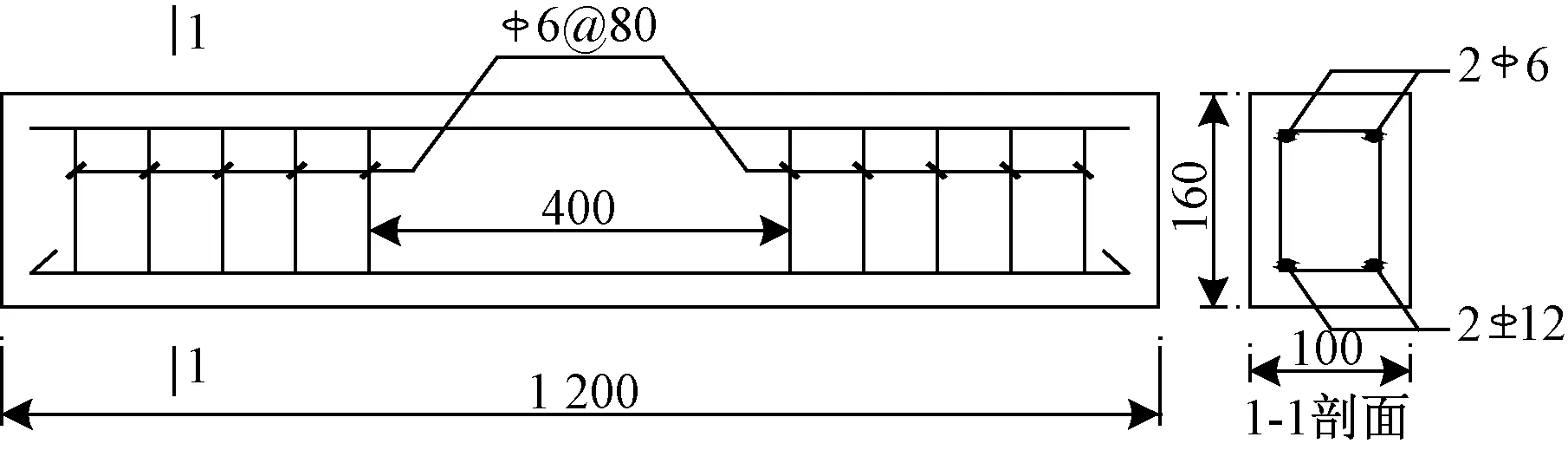
图2 钢筋混凝土梁配筋示意图(单位：mm)

2.2 试验装置

疲劳试验在MTS电液伺服疲劳试验机上完成，垂直荷载动静态最大值为500 kN，量程范围为±100 mm。腐蚀环境下疲劳试验装置如图3所示。

2.3 试验方法

钢筋混凝土梁的四点弯曲疲劳试验采用荷载控制，见图3。试验梁在自然环境下养护90 d后，将其置于盛有含不同浓度NaCl溶液(2.5%、3.5%、5%、10%)的腐蚀箱中，对试验梁浸泡1 d进行预腐蚀，然后将其放入疲劳试验装置中进行不同腐蚀环境下疲劳试验，与此同时施加杂散电流。试验参数设置为：应力水平r(即疲劳荷载极大值与试验梁的静载极限承载力比值：r=Fmax/Pu，式中Pu取75 kN)为0.6、0.7和0.8，加载频率为3.5 Hz，正弦波加载；氯离子浓度为2.5%、3.5%、5%、10%；杂散电流强度为10、20、30和40 V，具体试验方案如表2所示。疲劳荷载作用方式采用四点弯曲疲劳加载，四点弯曲试验梁的2个支撑点距离为1 000 mm。腐蚀箱中NaCl溶液静止液面与试验梁底部主筋齐平。杂散电流采用可控硅直流电源所提供的直流电进行模拟。试验梁主筋通过导线与电源正极、腐蚀箱中不锈钢板与电源负极相联。疲劳试验中，采用YHD-50动态挠度仪与306DF智能信号采集处理分析仪同步记录试验梁的跨中最大挠度dmax。因疲劳试验结果存在一定的离散性，所用数据结果均取3根试件试验数据的平均值。

图3 四点弯曲疲劳试验装置

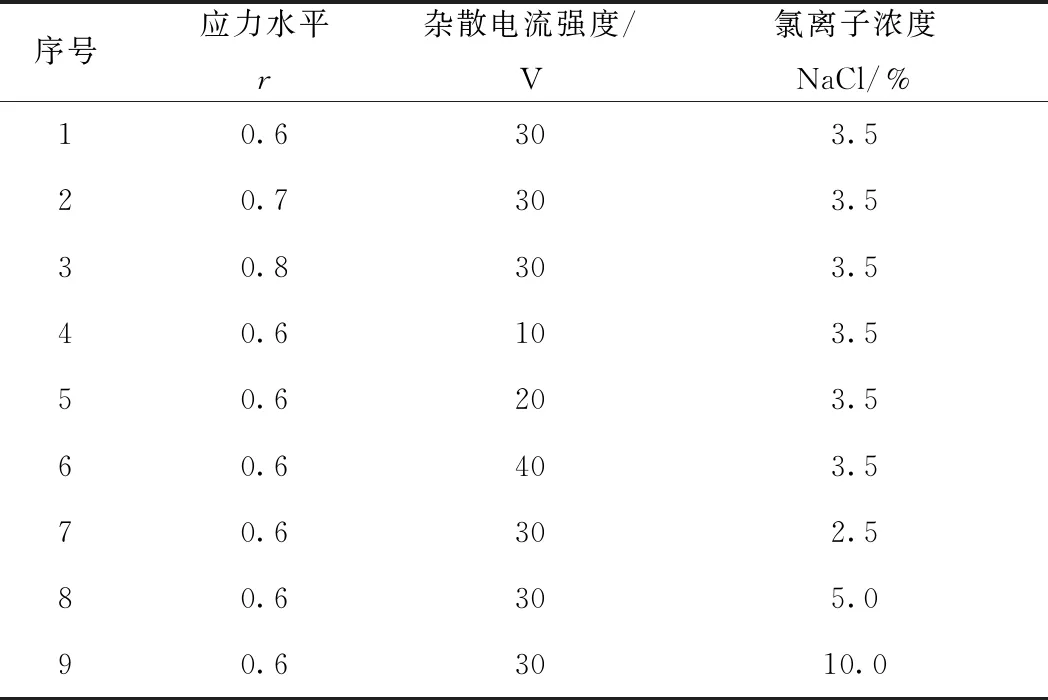
表2 试验方案

3 结果与讨论

3.1 跨中挠度演化

不同腐蚀环境下试验梁跨中挠度-循环次数演化过程见图4。由图4可知，挠度比值的演化过程呈明显的三阶段“S”形特征，具体为：初始阶段快速下降、中间阶段平稳下降和最后阶段损伤破坏急剧下降。图4中还给出了式(4)的模型理论预测值，如图中实线部分所示。从图4中理论预测值和试验结果比较可以看出，模型能够较准确地描绘钢筋混凝土试验梁跨中挠度演化的最初两个阶段。试验结果见图5，图5给出了对应于不同试验参数时模型参数B的变化规律，对应于不同试验参数时式(4)模型中系数b1、b2、b3回归值及其相关系数见表3。

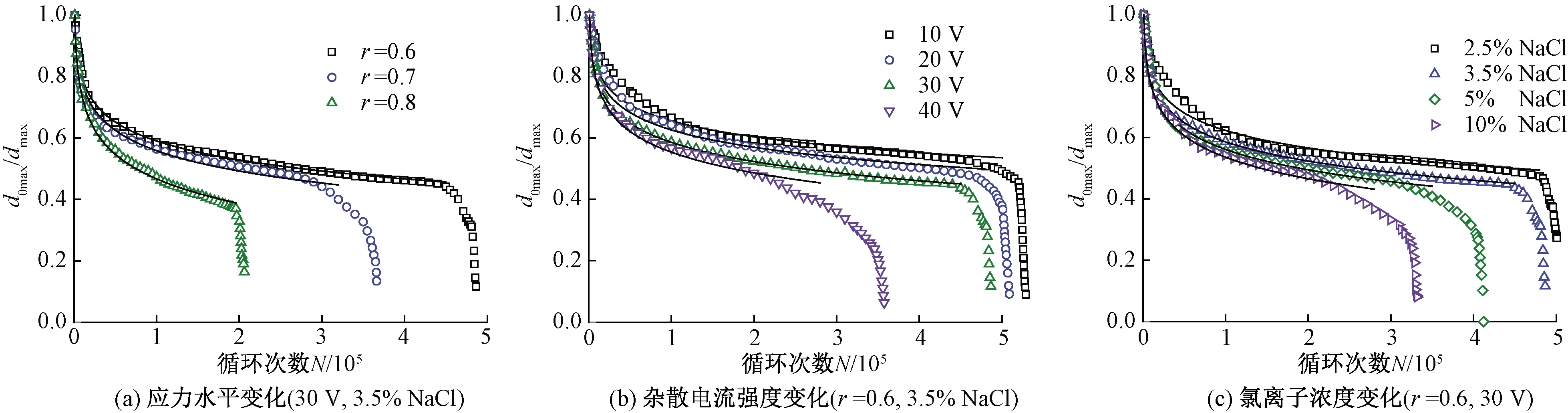
图4 不同腐蚀环境下挠度演化趋势

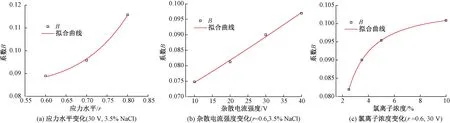
图5 系数B随影响因素演化关系

表3 试验数据拟合b1、b2、b3值

3.2 疲劳寿命预测

根据图4的试验结果，应力水平r、杂散电流强度及氯离子浓度变化时取刚度折减系数α分别为0.543 36、0.464 79和0.505 94，使用式(6)预测了不同试验参数变化下钢筋混凝土试验梁的疲劳寿命，预测值与试验结果比较如图6所示。

由图6可知，试验结果与模型预测结果吻合良好，说明本文建立的疲劳寿命预测模型是可行的和有效的。

由表3可知， 杂散电流强度为30 V，氯离子浓度为3.5%时，不同应力水平作用下地铁钢筋混凝土腐蚀疲劳寿命预测时B随应力水平r变化如下式，即

B=0.155 5r7.247+0.084 68

(10)

此时钢筋混凝土试验梁疲劳寿命预测模型，由式(6)和式(10)可得

(11)

为了考察杂散电流强度和氯离子浓度对钢筋混凝土试验梁疲劳寿命的影响，需要对式(11)进一步修正。设杂散电流强度与氯离子浓度的变化对疲劳寿命影响系数分别为记为KSC和KCl，则式(11)表示为

NFα(r,V,C)=KSC·KCl·Nif·

(12)

假定杂散电流强度30 V时对疲劳寿命影响系数KSC为1和氯离子浓度3.5%时对疲劳寿命影响系数KCl为1，那么，根据杂散电流强度和氯离子浓度对钢筋混凝土试验梁疲劳寿命的试验结果，疲劳影响系数KSC和KCl与杂散电流强度和氯离子浓度的回归曲线分别见图7(a)、图7(b)。

KSC和KCl的回归表达式分别为

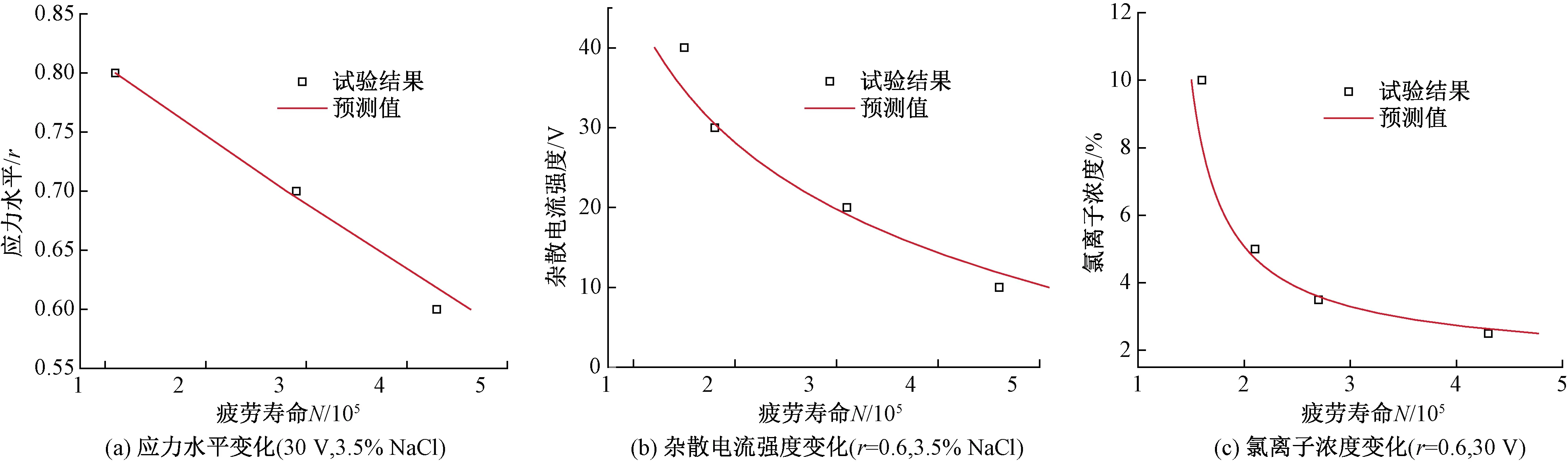
图6 不同腐蚀环境下疲劳寿命演化趋势

(13)

KCl=-2.676×10-6C3.061+1.084

(14)

式中：V为杂散电流强度，V；C为氯离子浓度，%。

将式(13)和式(14)代入式(12)，可得到杂散电流、氯离子和疲劳荷载共同作用下钢筋混凝土梁疲劳寿命预测公式为

NFα(r,V,C)=(-2.676×10-6C3.061+1.084)·

(15)

采用式(15)对杂散电流、氯离子和疲劳荷载共同作用下钢筋混凝土梁疲劳寿命进行预测，并将预测计算值与试验结果进行比较，对比结果如图8所示。

由图8可知，式(15)的预测理论值总体上与试验结果吻合较好，氯离子变化的情况下两者存在一定偏差。需要指出的是，由于疲劳试验时间和试验数据有限，式(15)并没有考虑杂散电流强度、氯离子浓度和应力水平之间存在的相互影响，该项工作有待下一步进行研究与完善。

图7 KSC和KCl回归曲线

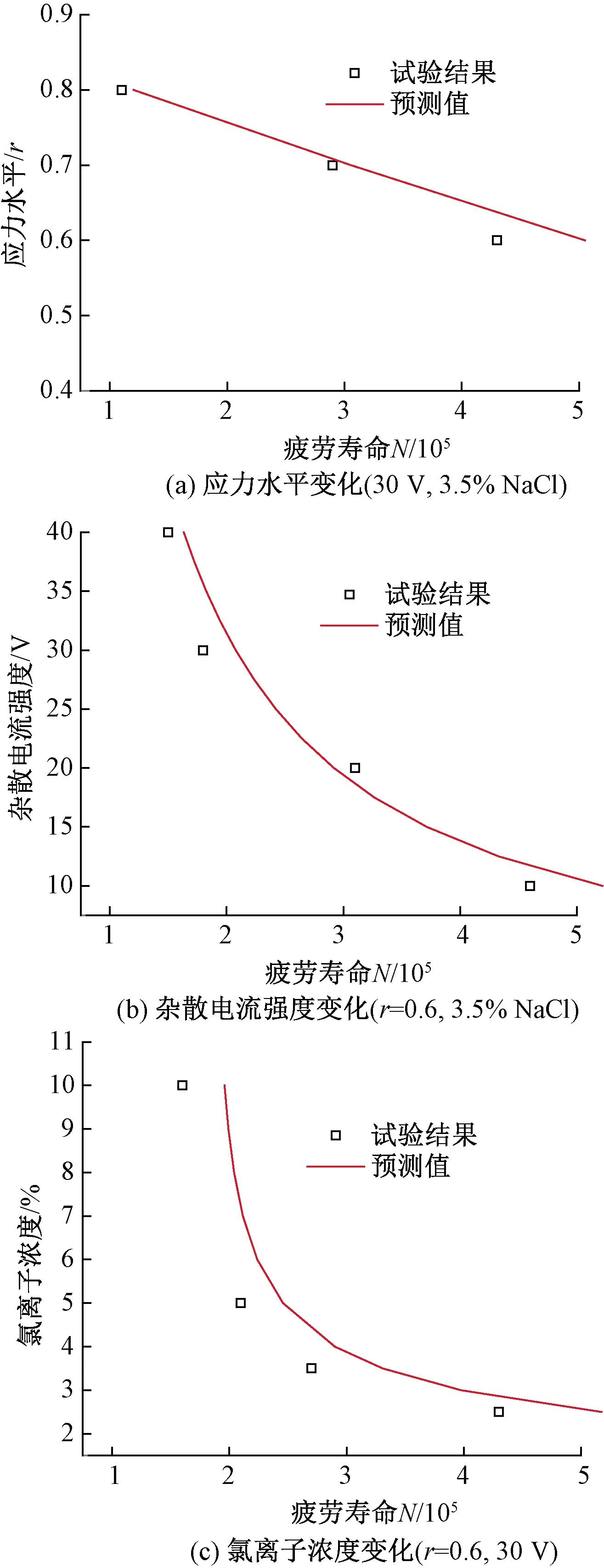
图8 疲劳寿命预测值与试验结果对比图

3.3 疲劳损伤预测

利用疲劳损伤模型式(9)，计算得到不同试验参数变化下的钢筋混凝土试验梁累积疲劳损伤演化过程，见图9。

由图9可知，无论是应力水平、还是杂散电流强度或氯离子浓度发生变化，试验梁疲劳损伤演化过程都大致相同。即在疲劳荷载初始循环次数中试验梁疲劳损伤发展较快，这主要归因于钢筋混凝土梁存在预腐蚀开裂，即初始损伤；经过一定循环次数后疲劳损伤便进入相对稳定发展阶段。当到达到试验梁疲劳寿命时，理论上名义损伤变量DF应该达到1。但图7中有些曲线末端DF并没有达到1，这可能应该归因于本文的分析中没有考虑试验梁的初始损伤和试验数据的分散性。

同理，为了研究散电流强度和氯离子浓度对钢筋混凝土试验梁疲劳损伤的影响，引入杂散电流强度与氯离子浓度对疲劳损伤的影响系数，分别记为DSC和DCl。依据式(9)，杂散电流、氯离子和疲劳荷载共同作用下钢筋混凝土梁疲劳损伤预测模型修正表达式为

(16)

同理，假定杂散电流强度为30 V时DSC取值为1和氯离子浓度为3.5%时DCl为1，那么，根据图9中疲劳损伤的预测结果，疲劳损伤影响系数DSC和DCl的拟合曲线如图10所示。

疲劳损伤影响系数DSC和DCl方程可分别表示为

DSC=-2.676×10-6V3.061+1.084

(17)

DCl=1.348 8C-0.234

(18)

因此，将式(10)、式(17)和式(18)代入式(16)，可得到任意杂散电流强度、氯离子浓度和疲劳荷载耦合作用时钢筋混凝土梁的疲劳损伤累积理论预测公式为

(19)

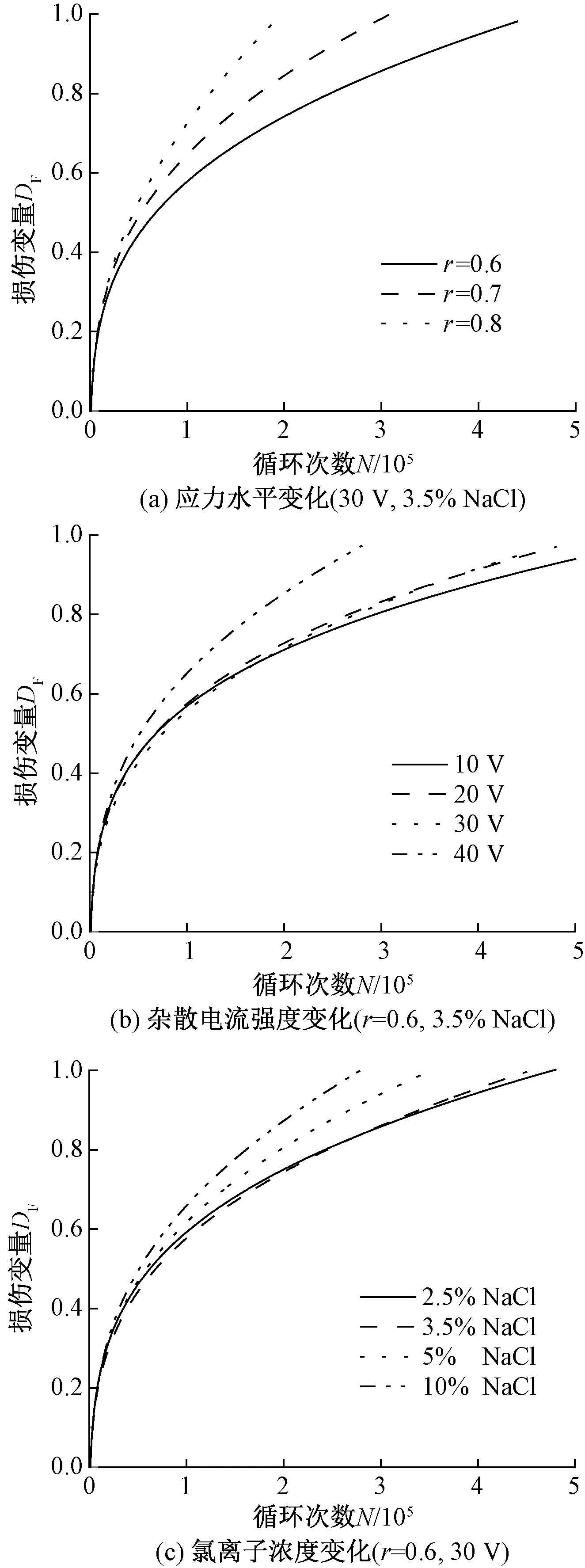
图9 不同腐蚀环境下累积损伤演化

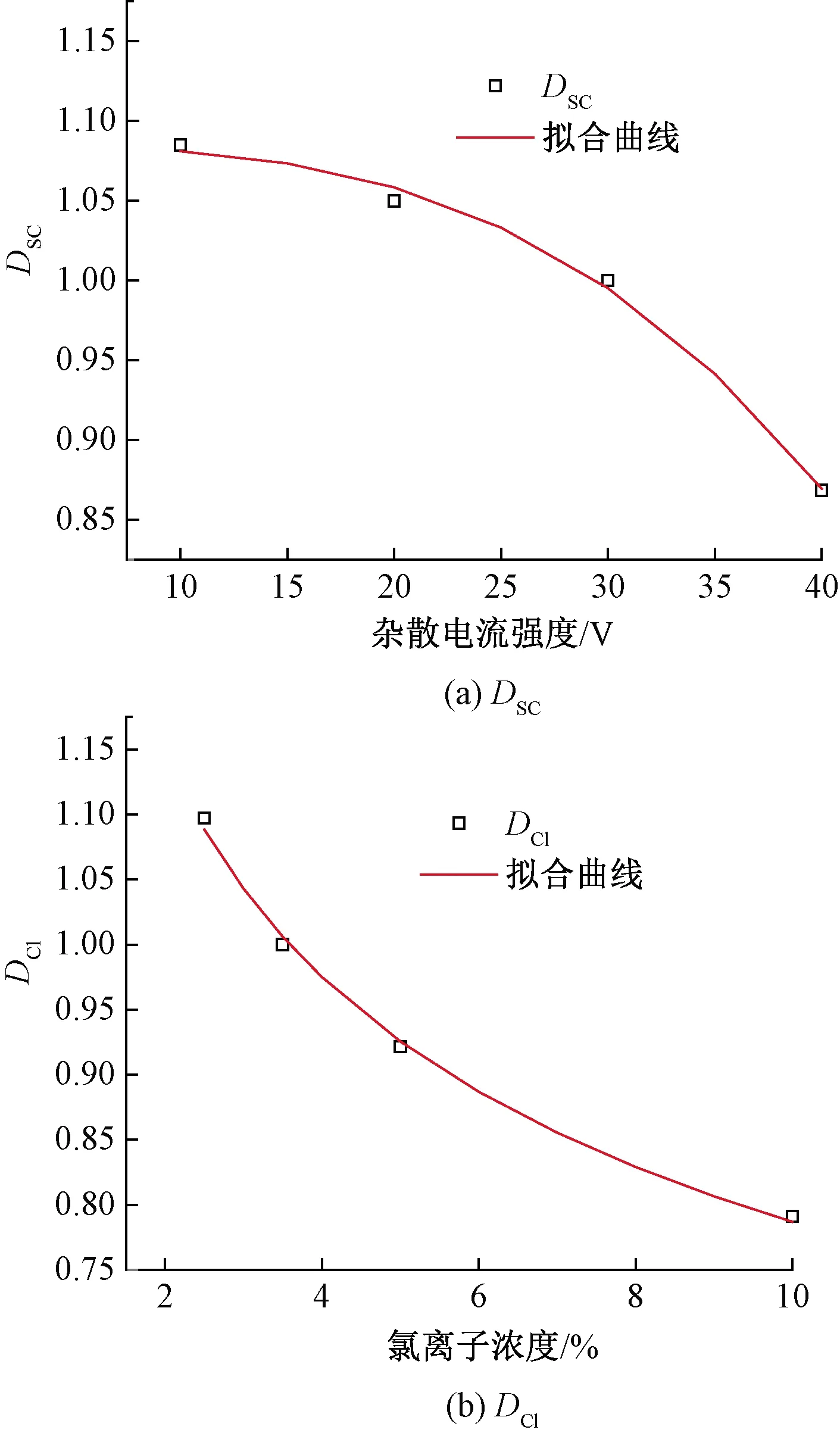
图10 拟合曲线

4 结论

本文依据地铁工程钢筋混凝土梁服役腐蚀环境和荷载工况，对钢筋混凝土梁进行了腐蚀-四点弯曲疲劳试验模拟和半经验理论分析。通过研究，得出以下结论：

(1)钢筋混凝土梁在杂散电流、氯离子等腐蚀环境和疲劳荷载作用下，其挠度演化呈三阶段“S”形特征。在疲劳荷载循环初始阶段挠度呈快速增加，而在试验梁疲劳损伤破坏阶段挠度则呈急剧增加，这两阶段在试验梁整个疲劳寿命中占据比极小，疲劳寿命主要由挠度演化平稳增加阶段控制。

(2)根据试验梁跨中挠度演化的试验结果，提出了挠度演化的半经验解析模型。模型预测值和试验结果比较证实该模型能够较准确地预测钢筋混凝土试验梁跨中挠度演化的最初两个阶段，说明了该模型的正确性。

(3)基于挠度演化的半经验解析模型，导出了杂散电流、氯离子和疲劳荷载共同作用下钢筋混凝土试验梁的疲劳损伤演化和疲劳寿命理论预测模型。经过进一步和试验结果比较，总体上证实了理论模型的可行性和有效性，但在反映氯离子浓度影响方面存在一定的偏差。

(4)模型参数与试验初始条件、腐蚀环境、荷载条件和材料属性等因素有关，它们可以通过试验数据回归得到。

(5)地铁工程钢筋混凝土梁疲劳损伤过程十分复杂，它与材料构成与性质、粗骨料和细骨料之间的粘合程度、钢筋与混凝土之间的粘合程度、腐蚀环境和荷载工况等因素有关。损伤过程包括初始损伤、损伤累积和损伤破坏三个阶段。

本文提出的地铁工程钢筋混凝土梁疲劳寿命和损伤演化预测模型方法是可行的和有效的，它能够较准确地预测在本文试验条件下钢筋混凝土梁的疲劳损伤演化情况和疲劳寿命，这在某种程度上可减少不必要的大量疲劳试验工作。由于地铁工程钢筋混凝土梁损伤破坏的影响因素复杂，本文仅针对杂散电流、氯离子和疲劳荷载等因素进行了研究，而且试验数据也不够全面，不能够反映这些因素之间的交叉影响。除此之外，还有干湿循环、加载方式以及其它腐蚀问题等，它们都对地铁工程钢筋混凝土梁损伤演化和服役寿命有影响，有待进一步更深入的研究。