计及分布式电源精确特性的配电网动态无功优化

荣德生，刘山林，刘健辰，宁 博

（1.辽宁工程技术大学电气与控制工程学院，葫芦岛 125105；2.国网辽宁省电力有限公司葫芦岛供电公司，葫芦岛 125105）

近年来环境保护、能源短缺、气候变化等问题引发各方的重视，分布式电源DG（distributed generation）以其经济、灵活、环保的特点越来越受到人们的关注[1-2]。随着DG大量接入配电系统，配电网由传统的单电源、辐射状结构逐渐变为遍布电源和负荷的复杂网络，且随着DG在配电网中渗透率的增加易引起线路功率越限，增大了配电网运行控制的难度[3]。无功优化是配电网中降低网损、改善潮流分布的主要方法。研究含DG的配电网动态无功优化，通过无功优化改善系统潮流分布，降低系统的有功网损，保证配电网安全稳定的同时提高配电网的经济运行，对我国的配电网升级改造，节能减排等具有重要意义。

含DG的配电网动态无功优化既要处理DG的无功出力，又要处理无功补偿分组投切电容器的投切组数和时间变量等整数变量，且配电网的潮流约束是非线性的，本质上是一个非线性非凸规划问题。目前国内外学者对配电网无功优化问题多采用非线性规划、二次规划等传统的规划方法或者采用启发式算法。启发式算法由于简单、复杂约束易模拟，在求解非线性规划模型中得到广泛应用，如遗传算法、粒子群算法、蚁群算法、免疫算法[4-7]等，能求解无功优化问题，减少损耗，但这些方法不能保证全局收敛，容易陷入局部最优。且动态无功优化寻求的是多时段下的全局优化，变量在各时段间有一定的耦合关系，增加了求解难度。近年一些国内外学者研究了交流潮流的二阶锥规划SOCP（second-order cone programming）凸松弛模型并广泛应用到配电网无功优化。文献[8]提出了将二阶锥松弛技术用于配电网潮流计算；文献[9-10]给出了辐射状配电网二阶锥松弛准确性的充分条件；文献[11-12]对配电网潮流凸松弛的准确性、可行性进行了分析；文献[13]将二阶锥松弛方法推广应用到最优无功补偿；文献[14-16]研究了混合整数二阶锥规划的动态无功优化。但都未精确考虑DG的节点注入类型，将DG接入节点处理为恒功率PQ型节点，忽略了DG所具有的多种运行控制方式对潮流优化问题的影响，且未将预测DG出力和负荷综合考虑，与实际情况偏差较大。已有的研究大多将PQ、PV、PI和PQ （V）类型DG直接近似处理为PQ型DG，即将无功出力近似固定为额定值。考虑到DG常常具有间歇性、随机性和不可控性，导致系统工作状态可能大幅偏离额定工作点，产生显著的误差。已有报道中，仅文献[17]精确计及4种类型的DG精确模型，但其采用微粒群启发性算法求解，无法保证全局最优解。

针对以上问题，本文提出一种有效的二阶锥松弛算法，求解含 PQ、PV、PI和 PQ（V）4 种类型 DG的配电网动态无功优化问题，给出了不同类型DG并网的模型转化方法，将动态无功优化问题转化为一个凸的混合整数二阶锥规划问题，降低求解复杂度，提高优化精度，保证全局最优。精确建立PQ、PV、PI和PQ（V）4种类型DG模型，避免产生建模误差，使优化结果更加符合实际情况，在保证支路电压、电流安全约束的同时考虑储能装置，离散无功补偿电容器作用于配电网的约束，以多时段有功网损最小为优化目标，根据预测DG出力和负荷曲线，以IEEE69节点系统为例进行仿真实验，验证所提方法的有效性。

1 动态无功优化模型

配电网的稳态运行方式均为辐射状运行，其某一支路拓扑结构如图1所示，其中，Pij、Qij为支路ij首端的有功功率和无功功率，Sij=Pij+Qij，Vi、Vj分别为支路ij的首、末端电压，rij、xij为支路ij的电阻和电抗，Pj、Qj为节点j注入的有功功率和无功功率，n（j）为网络中所有以j为末端节点的支路首端节点集合，m（j）为网络中所有以j为首端节点的支路末端节点集合，Nbus为电网节点数。

图1 配电网中某支路Fig.1 One branch of distribution network

以调度周期内的有功网损最小为优化目标，可得

式中：Ploss为总有功网损；t为时段；T为调度周期总时段数；Iij,t为支路ij在t时段的电流；Δt为时段间隔。其支路潮流约束为

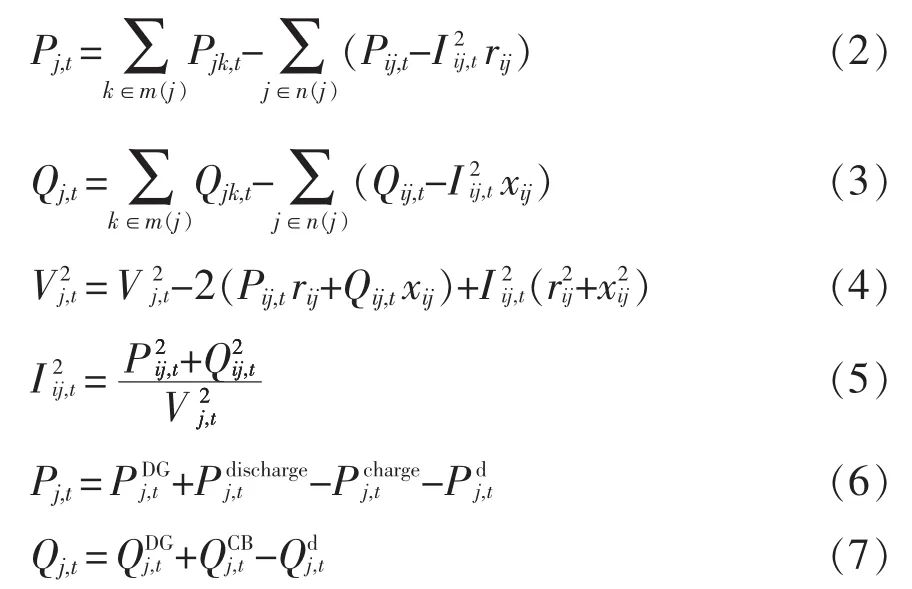
式中：Pij,t和Qij,t为t时段配电网中支路ij首端的有功和无功功率；Pj,t和Qj,t分别为t时段节点j注入的有功和无功功率；分别为 t时段节点j上DG注入有功功率、储能装置ESS放电功率、储能装置ESS充电功率、负荷有功功率；分别为t时段节点j上DG注入无功功率、电容器组CB的离散补偿功率、负荷无功功率。

储能装置ESS运行约束为

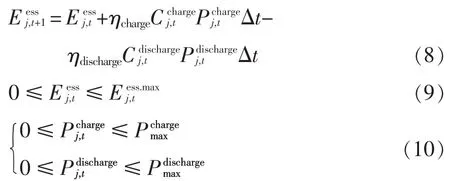
其和小于等于1，也就是储能设备不能同时处于充电和放电，只能处于充电、放电、不充不放3种状态中的一个。

电容器组CB运行约束为

2 分布式电源并网模型

传统配电网主要是平衡节点和PQ节点，随着DG渗透率的不断增加，如何精确处理不同类型的DG并网成为无功优化的重要前提。根据运行模式和控制特性，DG 可以分为 PQ、PI、PV 和 PQ（V）4种类型，设定各种DG在t时段节点j注入有功功率为，其无功出力如下。

（1）采用功率因数控制同步发电机作为接口的双馈感应发电机、内燃机与传统汽轮机等为PQ型DG，其无功出力为

（2）通过电流控制逆变器接入电网，如光伏发电、储能系统、燃料电池等为PI型DG，此类DG接入电网的电流Is恒定，则无功注入功率可表示为

（3）采用电压控制逆变器接入电网的光伏发电系统、部分风机、燃料电池、储能系统等为PV型DG。PV型DG的并网接口电压VDG通常为额定电压VN，PV型DG注入的无功功率由系统潮流决定，PV型DG并网接口变换器的容量有限，其无功注入满足

式中，M为一个任意大而非无穷大的正数。

（4）采用异步发电机并网的风力发电机属于PQ（V）型DG，其运行时需要吸收无功功率来建立磁场，采用补偿电容提供异步风机所需的无功功率以减少对电网的影响，降低网损。其实际注入无功功率为

式中：Qn为风机的无功补偿量；n为电容器投切组数；Qd为单位容量；Qs为风机吸收的无功功率；xm为励磁电抗；xσ为定子漏抗x1与转子漏抗x2之和。

此外，各类DG在各时段的投入功率都应满足

3 模型转化

由于配电网无功动态优化属于非凸规划问题，收敛性难以得到严格保证，且上述模型中包含的非线性约束式（2）～式（5）、式（16）、式（24）难以求解，对此利用二阶锥松弛技术将其转化成凸的二阶锥约束，降低模型复杂度，保证全局最优。令，潮流方程模型转化为

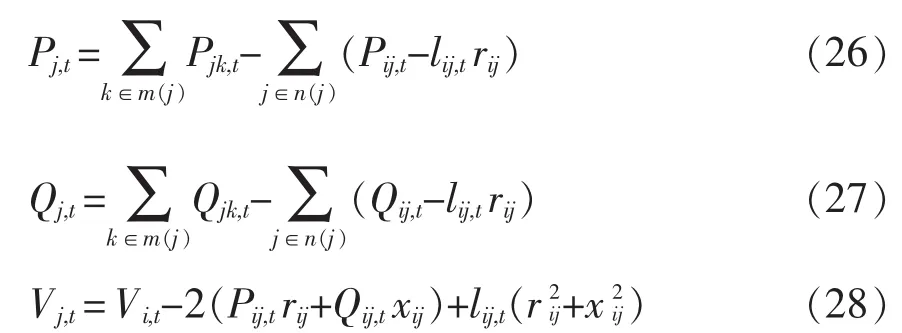
对式（5）进行松弛变化，将其转化为二阶锥约束，即

目标函数驱使lij,t逐渐减小使式（29）两边趋于相等，这也是二阶锥松弛收紧的过程，则松弛误差，可以保证解的精确性，经过等价变换写成标准二阶锥形式为

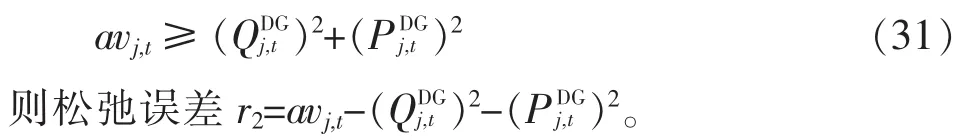
设 b1＞0，，式（24）松弛为二阶锥约束和线性约束，即

为使二阶锥约束式（31）、式（32）收紧，将目标函数变为

式（34）类似于多目标函数。式中，w1、w2为松弛部分的权重因子，根据接入的DG类型对w1、w2取值，如接入PQ型DG时w1、w2均为0，接入PI型DG时w1为1，w2为0，可以通过总的松弛误差反映优化结果的精确性，r=r1+w1r2+w2r3。

4 算例分析

在常见的IEEE69节点系统上验证本文方法的有效性。该系统的原始节点数据和线路参数等详见文献[18]。系统节点20为DG接入点，节点40为电容器补偿接入点，节点50为储能装置接入点，如图2所示，节点电压约束范围为0.92～1.02 p.u.。以一天为一个调度周期，分为24个时段，根据我国北方某地区2015年8月某日的24 h标么负荷曲线构造得到系统各节点24 h负荷数据，如图3所示[16]，DG预测出力如图4所示。在Matlab R2014b环境下基于Mosek算法包进行程序计算，系统硬件环境为i3-3110M CPU 2.4GHz，4GB RAM，操作系统为Win7 64bit。

图2 IEEE69节点配电系统Fig.2 IEEE 69-bus distribution system

图3 系统标么负荷曲线Fig.3 Per-unit load curve of system

图4 预测DG出力Fig.4 Predicted DG output

在节点20分别接入4种类型的DG，其中，PQ型DG的功率因数为0.95，PI型DG的控制电流为50 A，PV型DG的给定电压为0.98 p.u.，为1 000 kvar，为100 kvar，PQ （V）型异步风力发电机额定电压0.69 kV，经过变比为0.69/12.66的变压器并网，励磁电抗xm=2.205 9 Ω，定子电抗x1与转子电抗x2之和xσ为0.199 9 Ω，转子电阻R2=0.004 8 Ω。补偿电容器每组为100 kvar，投切组数为0～8，储能装置初始值均为100 kW，最大为300 kW，设定每次充放电充电功率最大为50 kW，假定ESS工作在理想状态时充、放电效率都为1。潮流计算结果见表1，无功优化前后各时段网损如图5所示。

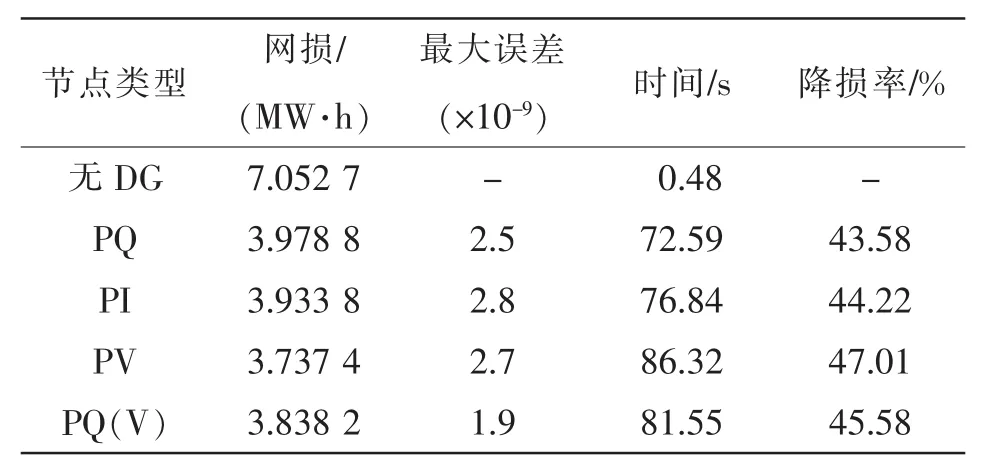
表1 不同DG潮流计算结果Tab.1 Power flow calculation results of different DGs

由表1可以看出，没有进行无功优化时，一天的网损为7.052 7 MW·h，时间为0.48 s；而加入DG优化后，网损明显下降，时间明显增多，这是因为预测DG下寻找最优结果迭代次数增加，而无DG接入时不需要寻优，只是进行潮流计算。各类DG并网后网损均有很大的降低，且最大松弛误差仅为2.8×10－9，可见其结果精确度较高。

以PQ型DG并网为例，电容器组在各时段的投切情况如图6所示，储能装置出力情况如图7所示，可以看出电容器组和储能装置得到一定的优化，ESS充放电调整系统潮流分布，在负荷比较大的16～18时段，储能装置放电较多，符合预期效果。

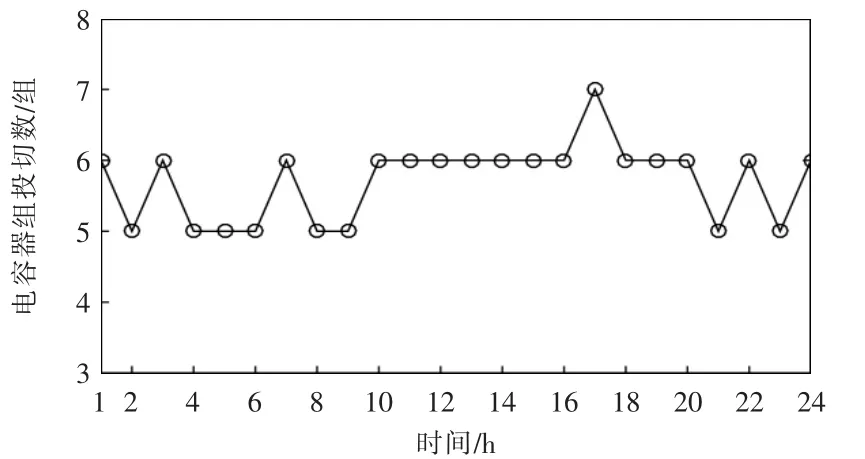
图6 电容器组全天投切情况Fig.6 Switching operation of capacitor bank in one day

图7 ESS各时段出力Fig.7 ESS output in each period

为测试本文方法的有效性，在前述负荷的基础上分别升高5%和10%、下降5%和10%，形成5个负荷场景，受环境影响负荷下降30%、升高30%、下降50%这3种变化模拟负荷曲线变化趋势差别较大的情况，其无功优化后的网损如图8所示。可以看到，负荷场景下调度周期内的网损变化趋势相近，都能有效降低有功网损，负荷曲线变化趋势差别较大的情况，该优化算法依然可以取得良好的有功网损优化效果。而在IEEE33系统[12]中节点14接入PQ型DG，节点20为电容器补偿接入点，节点28为储能装置接入点，网损下降幅度为41.33%，优化时间为21.6 s；在136节点系统[12]的节点20、40、80接入PQ型DG，节点60为电容器补偿接入点，节点50为储能装置接入点，网损下降幅度为27.44%，优化时间为217.6 s。可见本文模型在较小系统和较大系统中都取得了良好的计算效果。

本文PV型DG精确模型下的计算结果与文献[14，16]模型结果在同一系统下优化结果对比如表2所示。由表可见，文献[14]存在模型误差与松弛误差，总误差相对较大，网损下降相对较少；文献[16]模型中没有考虑DG的接入，网损下降较少；本文计及DG的精确模型，避免产生建模误差，优化结果更加符合实际情况，牺牲一些计算时间，达到更好优化效果。

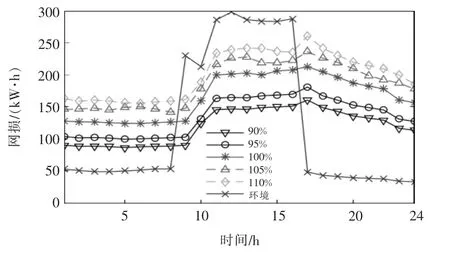
图8 不同负荷场景下每个时段的网损Fig.8 Network loss in each period under different load scenarios

表2 不同模型下的求解对比Tab.2 Comparison of solution among different models

5 结语

针对不同类型DG并网的动态无功优化这一复杂的非线性非凸混合整数规划问题，本文利用二阶锥松弛法将潮流方程中的非线性约束转化为二阶锥约束，给出了不同类型DG并网的模型转化方法，将动态无功优化问题转化为一个凸的混合整数二阶锥规划问题，降低求解复杂度，提高优化精度，保证全局最优。建立的动态无功优化模型能够精确地处理不同类型DG并网下的无功优化问题。算例表明多时段下的无功优化寻优效果明显，大大降低了网络的损耗且保证电压质量，为我国的电网升级改造，DG并网提供了依据，具有较强的应用价值。

本文采用优化算法包Msoek求解更大规模的系统时，计算时间较长，如何进一步降低DG并网多时段下寻优需要的时间，寻求更高效的无功优化以及对无功补偿设备的选址是有待进一步研究的课题。