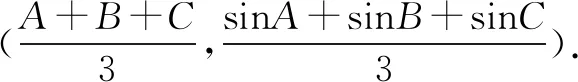借助转换思想 扫除数学解题障碍

王陈俊

(江苏省南通田家炳中学 226001)

对于高中阶段学生来说，数学是一门非常困难的学科，习题就是学生学习的拦路虎，想要帮助学生突破解题障碍，应当引导学生掌握数学思想方法，深入理解知识内容，对其进行转换和利用.转化思想是高中数学的重要思想方法，通过对题目内容的观察和分析，对其进行相应的转换，将原有问题转变成新问题，完成问题的思考和解答.运用转换思想解题，其关键点是发掘题目本质，了解知识点的形式，实现陌生问题向熟悉问题的转换，提高学生的解题效率.

一、深入分析概念性质，巧妙利用转换思想

有些数学题目看似题目信息不全，缺少一些解题条件，学生想要很好地完成解题，需要挖掘题干中的概念，加深对概念性质的理解，再结合概念性质完成转化，明确解题思路，突破学生解题障碍，有效解决数学问题.

例1已知数列{an}为等差数列，Sn是其前n项和，如果3S3=S2+S4，a1=2，则a5=( ).

A.-12 B.-10 C.10 D.12

在整个题目的思考和解题中，需要对题干中的“等差数列”进行分析，在这个概念中包含着等差数列的性质，属于隐含性条件.结合问题的分析，灵活利用数学性质，实现问题的有效转化，提高学生的解题效果.

二、注重解题思维转化，突破数学解题障碍

高中数学解题中，部分数学题目的难度比较大，按照常规方式解题比较困难，影响学生解题效率.作为数学教师，需要根据数学题目进行分析，实现学生解题思维的转化，帮助学生找到解题关键点，突破数学解题障碍，提高学生的解题质量.

例2已知x，y，z三个数字为正数，并且成等差数列，求证：x2-yz，y2-xz，z2-xy也是等差数列.

在解答此题的过程中，如果学生从正面进行解答完全没有解题思路，解题会非常困难.在这样的情况下，让学生利用逆向思维解题，根据求证的结果进行反向推导，通过充分必要的推导，避免学生解题疏漏，保证解题效率和准确性.

如果x2-yz，y2-xz，z2-xy为等差数列，则有2(y2-xz)=x2-yz+z2-xy.

所以2y2+(x+z)y=(x+z)2.

因为x,y,z为等差数列，所以2y=x+z.

所以等式成立.

因此，x2-yz,y2-xz,z2-xy为等差数列也成立.

高中数学解题中，一些问题通常正向求解比较复杂，教师可以引导学生转化解题思维，借助逆向思维进行推导，实现求解问题的转换，借助相应的推导验证，完成题目思考和解答.

三、深入发掘隐含条件，利用转换思想解题

高中数学教学中，知识内容比较多，数学问题中的知识点相互联系，使得问题更加复杂，增加了解题难度.因此，在解题的过程中，需要引导学生发掘题目中隐含的条件，有效利用转换思想，降低题目解答难度，找到问题解题思路，完成题目的有效解答.

例3数列{an}为等比数列，其前n项和为48，前2n项和为60，求解其前3n项和是多少？

首先假设其前3n项和是S，通过对题目条件进行分析，发现其前n项和、前2n项和与前3n项和有着共同的联系.前2n项其实是前n项和次n项的组合，而前3n项和则是在前2n项的基础上加上后n项和组合而成.通过这样的分析，得出次n项和为12，后n项和为S-60.同时，题目中隐藏着另一个条件，即等比数列前n项和、次n项和与后n项和是等比数列.学生通过对这个隐藏条件的发掘和利用，计算得出S=63.

因此，在解题的过程中，深入发掘题目的隐含条件，根据题目条件进行分析，结合知识点之间的联系，完成问题的转换，突破解题中的困难，从而提高学生解题的效果和质量.

四、利用数形转换思想，明确问题解题思路

不等式问题是高中数学的重要问题，在解题中利用转换思想，通过图形将抽象问题展示出来，能有效解决数学问题.在解题过程中，数形转化是常见的方式，将代数问题转化成几何问题，可以提高学生的解题效率.根据问题中的已知条件，实现问题形式的转换，借助图形的辅助分析，解决数学问题.

通过观察题目，可以得知此题属于正弦三角函数问题.构建相应的函数y=sinx，且0

相对于初中数学来说，高中数学知识的难度非常大，并且知识内容更加复杂.在学生解题的过程中，由于知识基础、思维方式等限制，使得学生出现解题障碍.面对学生的解题障碍，教师应当引导学生利用转换思想，借助多样化的方式，实现问题对象和目标的转换，转换解题方式和思维，降低解题难度，提高解题效果.高中数学解题教学中，转换思想是重要的数学思想，实现复杂问题简单化，借助直观方式展示抽象问题，需要灵活利用，提高解题效率.