光伏电池热电压动态模型及其仿真分析
刘 昶,肖志权,杨 炎,张家昌,杨剑尧
(1.武汉纺织大学机械工程与自动化学院,湖北 武汉 430200;2.广州穗华能源科技,广东 广州 510000)
当今世界,化石燃料的消耗,能源的短缺注定会是我们将要面临的问题,研究可再生能源发电系统,如光伏发电系统有了重大意义。构建实际工况下光伏电池输出电流I与电压U之间的关系曲线,是研究光伏发电技术的必要前提。
很多学者对光伏电池的建模问题进行研究,得到了一些可行的数学模型,但很多模型存在着一些缺点,例如,文献[1]通过在光伏电池三参数模型的基础上,提出了光伏电池的Bezier函数建模方法。该方法建模过程繁琐,且在构建过程中控制点的选取容易造成误差。文献[2]利用Lambert W函数推导了光伏组件的显式单二极管模型,提出一种基于重启边界约束Nelder-Mead单纯形算法的参数提取方法rbcNM,缺点在于采用了复杂的智能算法增加了模型的复杂性和求解难度。文献[3]提出简化单二极管模型中的电阻,将电流方程由隐式方程转化为显式方程,缺点是忽略了电阻后与光伏电池实际误差较大。
因此,如何建立简单、准确的光伏电池工程用数学模型成为太阳能应用领域中的重要问题。本文对光伏电池的单二极管模型进行研究,引入光伏电池热电压,得出光伏电池的热电压模型,引入环境修正公式,得到光伏电池的热电压动态模型。通过对仿真结果的分析表明,该模型与光伏电池输出特性匹配度好,为光伏电池最大功率点跟踪提供了参考。
1 光伏电池等效电路模型
光伏电池由半导体二极管组成,半导体的P-N结在太阳光的照射下将光能转换成电能。在光照强度一定时,光生电流Iph可以看作一个恒流源,即每片光伏电池单元可以看作是一个恒流源与一只正向二极管的并联回路,假设二极管支路的电流为IDO,光伏电池等效并联电阻为Rsh,光伏电池板前后表面的电极以及材料引起内部串联损耗为Rs,其等效电路模型的典型形式是单二极管形式,如图1示。

图1 光伏电池单二极管等效模型
光伏电池等效电路模型对应的输出特性方程为:

式中:V、I分别为光伏电池的输出电压和电流;Iph为光生电流;IDO为P-N结等效二极管的反向饱和电流;q为电子电荷(1.602×10-19C);A为P-N结等效二极管理想因子,一般取值1~1.25;T为电池温度;K为Boltzman常数(1.38 × 10-23J/K);Rsh、Rs分别为等效并联电阻和等效串联电阻[4]。
2 光伏电池热电压动态模型的建立
2.1 四参数行为模型
在光伏电池模型中,使用最广泛的是单二极管模型,是代表了准确性和简单性之间的良好折中,考虑在单二极管模型的基础上进行改进。
式(1)为光伏电池的单二极管模型方程。式中包含了光生电流Iph、二极管反向饱和电流IDO、串联电阻Rs、并联电阻Rsh、二极管理想因子A等五个未知参数,故被称为光伏电池的五参数模型。该方程为隐式方程无法直接求解。
目前工程上为了分析的简便与实用就在式(1)的基础上进行了工程简化推导,将其变为显性表达式,忽略Rs、Rsh的影响简化为下列式子[5]:

式中:I为输出电流;V为输出电压;Isc为短路电流;Voc为开路电压;C1、C2为未知数。C1、C2可由最大功率点处电压Vmpp、电流Impp、短路电流Isc,开路电压Voc求出,式(2)中只有Isc、Voc、C1、C2这四个未知参数,故称为四参数行为模型(后面全部称作四参模型)。然而进行仿真时,发现仿真得到的输出特性曲线与实测曲线的误差较大,特别是不同温度下的输出特性曲线明显不符合光伏电池的温度特性[5]。
2.2 热电压模型
在式(1)中,有电子电荷q、P-N结等效二极管理想因子A、电池温度T、Boltzman常数K四个参数,由此引入热电压的概念。由热电压公式VT=ATK/q,对式(1)简化得:

该方程为输出电压V、电流I的隐式方程,无法直接求解,需要对该式进行一些化简。通过忽略分流电阻Rsh,以闭合的方式求解方程,电压可表示为电流的解析函数;同样,忽略串联电阻Rs,电流可以表示为电压的解析函数[6]。
由相关文献[5]可知,串联等效电阻对光伏电池的输出功率影响较大,串联等效电阻越小,光伏电池的功率越大,最大功率点越高,等效电阻Rs对光伏电池的输出功率影响较大,不可忽略。
并联电阻Rsh是P-N结生产制造过程中产生的,Rsh增大会导致开路电压减小,短路电流基本不变,对电池的影响不大。又由于Rsh值为千欧级,流过其上电流近似为零,因此在简化的建模中可以不予考虑[7]。
故在光伏电池的实际等效简化过程中,忽略并联电阻支路的影响,保留串联电阻Rs,并经过移项化简后,式(3)被简化为:

式中:V为输出电压;VT为热电压;Iph为光生电流;IDO为二极管反向饱和电流;Rs为串联电阻;I为输出电流。
在等效电路开路的情况下,输出电流I=0,即可得出IDO:

联立求解式(4)、(5),并化简得:

由于短路电流Isc相对于二极管反向饱和电流IDO来说特别大,可以假设短路电流近似等于光生电流,且由于热电压VT远小于开路电压Voc,综合这两点式(6)近似表达为:

式(7)即为改进的单二极管串联模型-热电压模型。图2描述了式(7)的等效电路。
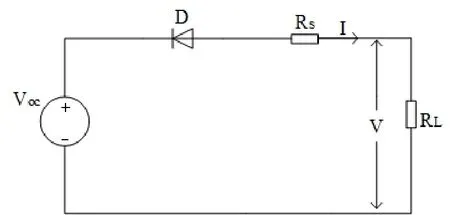
图2 热电压模型等效电路
此模型具有传统单二极管模型相同的输出特性,由于Voc与Isc的获取十分简单,通过查表可知,该模型的确立只需要确定热电压VT以及串联电阻Rs即可,相对来说更加简单。
由于热电压VT和串联电阻Rs是两个未知量,由式(7)的最大功率点及其定义联立可求出串联电阻Rs和热电压VT:
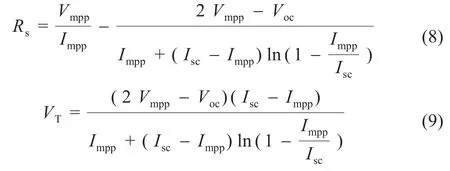
2.3 热电压动态模型
外界环境对光伏电池的参数影响很大,当在不同光照强度和环境温度时,引入环境修正公式十分必要,此时光伏电池的模型需要考虑开路电压、短路电流、热电压的变化。美国桑迪亚国家实验室(Sandia National Laboratories)基于实验数据的光伏电池参数模型参数修正公式,得出了环境对光伏电池参数影响的表达式[8]:
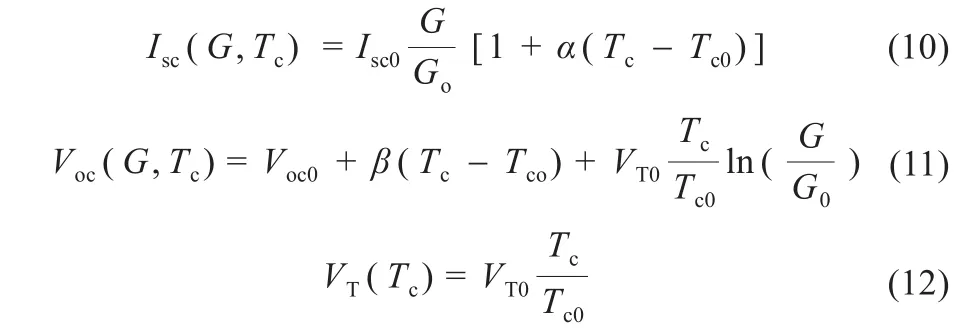
式中:Isc为短路电流;Voc为开路电压;VT为热电压;Isc0、Voc0、VT0分别为标准测试环境下光照强度1 000 W/m2和光伏电池温度298 K时的光电流、开路电压、热电压;Tc为电池温度;α和β分别为短路电流温度系数和开路电压温度系数;串联电阻Rs随温度变化很弱,故可认为是一个常数[9]。
式(7)表达了对单二极管模型简化后的模型,引入热电压的概念,提出电压串联-热电压模型,然后加入开路电压、短路电流、热电压相对于温度与光强的修正,由于热电压只随温度变化,是一个动态的参数,且开路电压、短路电流都是随着温度及光强动态变化的,所以将式(7)与式(10)、(11)、(12)联立称为热电压动态模型。
3 热电压动态模型的建模分析
3.1 热电压动态模型的MATLAB/Simulink建模
利用简化的工程数学模型在MATLAB/Simulink中进行建模,本文选用的是某光伏公司所产的260 W光伏板进行建模仿真。根据出厂参数可知,该电池在标准状况下(AM为1.5,298 K,1 000 W/m2),最大工作电流Impp=7.47 A,最大工作电压Vmpp=34.8 V,开路电压Voc=44 V,短路电流Isc=8.09 A,A取1,短路电流温度系数α=0.000 317 A/K,开路电压温度系数β=-0.187 4 V/K[10]。
将上述数据代入式(8)(9)中,得出Rs=0.307 Ω,VT=2.7 V,将其代入式(9),且在Simulink中进行建模,并将数据代入式(10)~(12)得出修正后的参数,再将公式中的各组成参数分别建模封装,可得到如图3所示仿真模型。
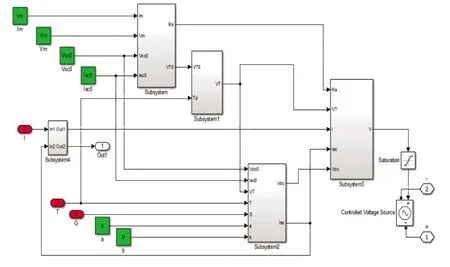
图3 仿真模型
3.2 仿真结果分析
利用Simulink建立的光伏电池热电压动态模型进行改变光照强度G和温度Tc的仿真,可以得到如图4、5的仿真结果图。
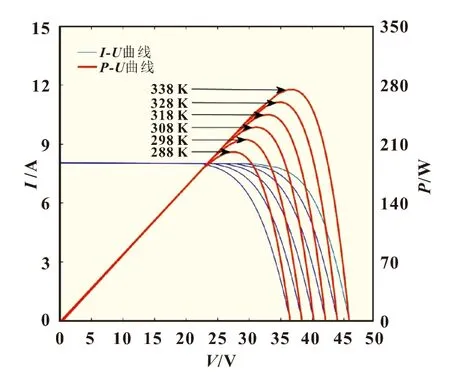
图4 G=1 000 W/m2时,不同温度下的P-U和I-U图
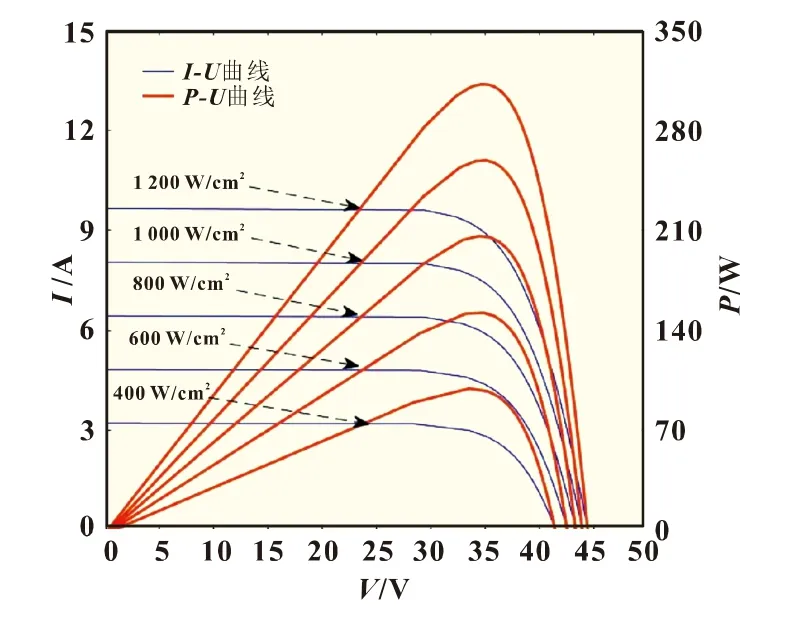
图5 298 K时,不同光强下的P-U和I-U图
图4中,在G=1 000 W/m2的标准光照强度下,改变温度由288~338 K,得到温度对光伏电池输出功率及输出电流的影响。温度越高,光伏电池的最大功率点越低,光伏电池的输出功率下降,开路电压越小。负载电压较小时,改变温度,输出电流变化不大,在负载电压接近开路电压时,输出电流开始不同程度的下降。
图5中,在298 K的标准温度下,改变光照强度,得到光照强度对光伏电池输出电流及输出功率的影响,可以看出光照强度越强,光伏电池的最大功率点越高,光伏电池的输出功率也越大,短路电流和输出电流也越大。
由于光伏电池的等效模型为超越方程,Simulink环境下的仿真模型难以建立,为了验证热电压动态模型的准确性,进行热电压动态模型仿真与四参模型仿真结果的比较。四参模型的仿真来源于参考文献[10],在四参模型的基础上,加入环境修正方程,得到仿真结果。图6和图7为不同光强与温度下的两个模型最大功率的比较曲线。
图6是在相同的温度下,改变光照强度进行的两种模型的最大功率Pm的对比。由图可知,随着光照强度的增加,在最大功率方面,热电压动态模型与四参模型差距是越来越大的。温度由298 K变化到343 K时,相对误差由0变化到最大的7.7%。温度在298 K以上时,热电压模型优于四参模型。同时在相同的温度下时,光强越大,两条曲线的差距也越大。因为四参模型忽略了串联电阻Rs,即四参模型Pm相比于光伏电池实际Pm偏高,所以热电压动态模型Pm更加靠近光伏电池的实际Pm,温度影响热电压模型的精确程度,温度越高越精确。

图6 不同光强下不同模型最大功率Pm比较
图7是在相同的光强下,改变温度进行的两种模型的最大功率Pm的对比。光强越小,两曲线的交点处的温度越大,温度不超过298 K;光强越大,两曲线交点处温度越低;在光强相同的情况下,温度越高,差距越大,最大相对误差为9.1%。因为四参模型忽略了串联电阻Rs,即四参模型Pm相比于光伏电池实际Pm偏高,所以热电压动态模型Pm更加靠近光伏电池的实际Pm,光强越大,热电压动态模型的适应性越好,越精确。

图7 不同温度下不同模型最大功率Pm比较
3.3 热电压的影响
图8是在标准工况即298 K、1 000 W/m2下得到的改变热电压的P-U和I-U曲线,从图中可以看出热电压越大,光伏电池的最大功率点越低,开路电压与短路电流不变。
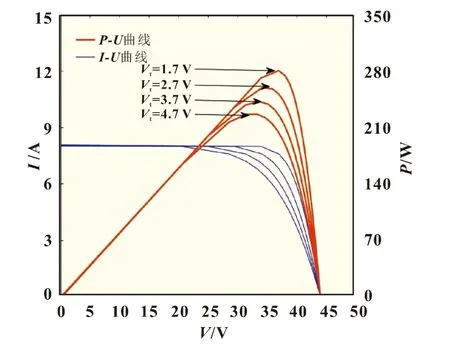
图8 改变热电压的P-U和I-U曲线
4 结论
本文将光伏电池等效模型进行了简化,使得模型只需要获得厂商提供的短路电流、开路电压以及最大功率点的电压电流这四个参数就能计算出热电压模型的所有参数。建立了光伏电池的热电压动态模型,同时在MATLAB/Simulink环境下进行了基于模型的改变光强和温度对模型的模拟和分析。与四参模型进行了仿真结果比较,结果表明在298 K以上环境中,热电压动态模型的最大功率Pm始终小于四参模型的最大功率Pm,最大功率Pm的最大相对误差达到9.1%,由于四参模型Pm比实际光伏电池Pm偏大,所以热电压动态模型优于四参模型,且温度与光强越高,相对误差越大,温度是主要影响因素。热电压动态模型在实际工程建模仿真的应用中,可以比较准确地建模和评估光伏发电系统的输出功率及效率。

