基于电压偏移序列的电池健康状态估计方法

叶健诚，叶建德， 杨洪涛

(国网电力科学研究院有限公司实验验证中心，江苏 南京 210000)

锂离子电池在持续使用过程中不能避免老化和性能衰减，也进一步制约着电动汽车的使用寿命和安全可靠性[1]。精确的SOH估计不仅为电池组荷电状态(state of charge,SOC)提供依据，也能有效避免电池的过充、过放和加速老化。数据驱动方法是根据锂离子电池历史数据进行建模，使用模型和机器学习等方法实现电池健康状态估计的方法，这种方法的优点是不需要深入理解电池的老化机理，但需要大量的历史数据进行模型训练，且算法精度受数据质量的影响[2]。而电池衰退机理模型虽能有效地分析各个部分的退化规律，但复杂的经验模型计算使其无法用于实际工况[3]。基于容量增量曲线(IC曲线)的SOH估算方法不仅能够有效表征内部老化路径机理层面，还能从IC曲线上提取可以反映电池老化的特征参数，包括峰高度、峰位置和峰面积[4-5]等，并结合数据驱动的方法[6]建立容量估计模型[7-8]。基于IC曲线的估算方法需要全SOC区间的数据，而在实际应用过程中初始SOC依赖于驾驶员充电意图，说明现有的方法难以用于实际工况。因此，研究出一种能采用少量历史数据并考虑驾驶员充电意图的SOH估算方法十分重要。

为解决现有方法依赖于驾驶员充电意图和数据质量的问题，本文提出一种以新电池的充电曲线为基准，分区间构建电压偏移序列的估算方法，并采用PCA方法提取序列的分布特征，建立不同初始SOC下的SOH估算模型。实验结果表明：该方法能利用少量的历史数据进行快速的SOH估算，在不同初始SOC下的SOH估算最大误差仅为1.10%，在初始SOC误差±5%下的鲁棒性，电池SOH估算最大误差仍能保持在4%以内。

1 基于电压偏移序列的特征分布

基于电压偏移序列的电池健康状态估计方法分为构建电压偏移序列、提取特征参数、建立回归模型三个部分，在任意初始SOC下充电过程的算法流程如图1所示。

1.1 构建电压偏移序列

(1)获取实验数据：选取10只相同型号但不同老化状态的样品三元锂电池Li[Ni0.8Co0.1Mn0.1]O2，进行25℃1C倍率下的充电测试，样品电池标定的SOH值如表1所示。

图1 算法流程图

表1 样品电池健康状态标定 %

(2)重构基准序列：以表1中标定SOH大于96%的样品电池作为基准样品，并以步骤(1)中所测得全区间充电电压曲线为基线，记SOC和电压分别为Sb、Ub。根据基线bl构建1%等分间距的序列SOC0和充电电压序列U0=[U01,U02,…,U0N]T，以SOC0-U0为基准序列，其中N为基准序列的长度。

(3)重构老化序列：将步骤(1)中所测SOH小于96%的样品电池作为老化样品。按照步骤(2)中构建1%为等分间距的老化SOC序列SOCj和端电压序列Uj=[Uj1,Uj2,…,UjM]T，其中j为SOH值，M为老化序列的长度。

(4)选取数据区间：如图2所示，由于驾驶员不确定的充电意图，设可充电的初始SOC分别为10%，20%，30%，40%。假设充入电量大于10%的，选取每10%为一个间隔，如图2黑框所示区域，从而获取4组数据区间。因此，仅需起始SOC值即可确定构建电压偏移序列所需的数据区间。

图2 不同初始SOC下的基准序列和老化序列

(5)构建电压偏移序列：按步骤(4)中SOC初值选取的数据区间，并以步骤(2)和(3)中重构的基准序列SOC0，U0和老化序列SOCj、Uj为基本数据，选择特定SOC区间内的基准和老化序列，取L为重构序列长度，电压偏移序列的计算公式如下：

式中：URj=[UR1,…,URL]T；UR0=[UR01,…,UR0L]T。

1.2 序列分布特征分析

根据上一节所述构建电压偏移序列的步骤，以样品编号的电池为例，假设编号6的初始充电SOC为5%，在充电过程中选取10%～20%SOC区间的电压数据构建电压偏移序列。该序列的频数分布特征如图3所示，在0～100 mV的电压偏移量中分布特征呈正态分布。

图3 电压偏移序列的分布直方图

为确保所有样品电池的4组电压偏移序列均满足正态分布，进行Kolmogorov-Smirnov检验，结果表明p值均小于0.05且满足正态分布特征。因此以正态分布来描述全寿命周期的序列分布特征：

治疗后24 h尿微量白蛋白和24 h尿蛋白定量对比：观察组均低于对照组，差异有统计学意义（P＜0.05）。见表3。

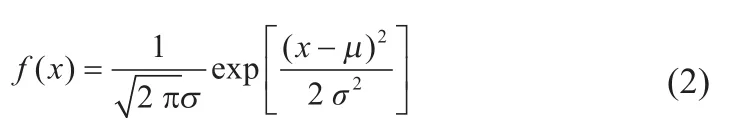
式中：μ、σ分别为正态分布的均值和方差。

2 基于主成分回归的SOH估计模型

2.1 分布特征提取

针对10只样品电池在不同SOC初值下的电压偏移序列e的分布特征进行分析，提取可表征该序列分布状态的特征值。均值、四分之间距、峰度、偏度计算公式分别如(3)～(6)所示：

式中：eave为均值。

Q用以表征分布的离散程度，反映各数据远离其中心值的趋势。其计算公式如下：

式中：Q1和Q3分别是1/4分位数、3/4分位数。

峰度Kurt表征概率密度分布曲线在平均值处峰值高低的特征数，其计算公式为：

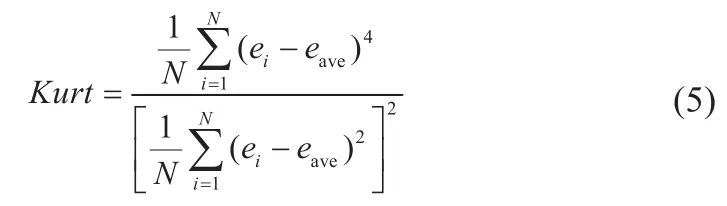
偏度Skew是统计数据分布偏斜方向和程度的度量以及统计数据分布非对称程度的数字特征。其计算公式如下：

根据式(3)～(6)计算4个分布特征参数，进一步以较少特征参数和计算量的原则筛选有效特征值。首先对不同初始SOC下的4个分布特征参数与SOH的相关性进行分析，其相关系数如表2所示。

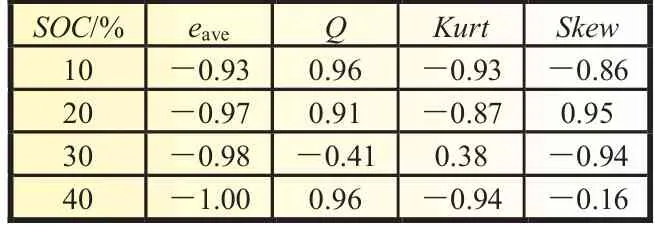
表2 特征参数与SOH的相关系数

如表2中各特征参数相关系数所示，在初始SOC分别为10%、20%、30%和40%的条件下，随机统计量eave、Q1、Q2、Q3与电池的健康状态之间均存在高度负相关性，且相关度均大于0.93。因此可判断4个特征存在严重的多重共线性，并且由于eave计算简单作为第一有效特征。为了防止多重共线性引起的模型失真，以方差膨胀因子(VIF)定量表征共线性严重程度，VIF=187＞100，说明变量之间存在较严重的共线性，不能直接使用简单的多元线性回归直接估计。其中KMO值是表征数据是否适用于PCA分析的参数，介于0～1之间，其值越接近1说明数据越适用于PCA分析。特征参数数据的KMO值为0.709，说明PCA方法适用于此数据的多重共线性处理。

2.2 基于主成分回归法的SOH模型

主成分回归的一般步骤为：

(1)标准化处理：把原始自变量和因变量数据标准化，计算公式如下：

式中：Zxi为任意变量标准化之后的特征参数；μi、σxi分别为第i个特征参数正态分布的均值和方差。

(2)主成分分析：对原始变量进行主成分分析，根据特征值和累积解释程度确定主成分个数N。

(3)主成分回归：将步骤(2)获得的主成分对标准化后的因变量进行普通最小二乘回归，得到主成分与标准化后的因变量多元线性关系。

(4)建立标准化参数之间的关系：将步骤(2)中获得的主成分与原始变量的关系代入式(3)中，获得标准化因变量和标准化原始变量的关系。

(5)逆标准化：按照式(1)将各自变量与因变量还原到非标准化数据，得到因变量与自变量的关系。

按照上述步骤进行初始SOC的主成分回归，PCA分析结果可知两个主成分的累计方差百分比达到98.97%，说明两个主成分包含原4个变量98.97%的信息，因此选择前两个主成分并命名为Zp1和Zp2。根据载荷矩阵与主成分的特征值，计算得到Zp1和Zp2的表达式：

按照式(8)(9)计算得出Zp1和Zp2的数据。将Zp1和Zp2作为自变量，标准化后的SOH值Zs作为因变量，使用最小二乘法建立回归模型，得出Zp1、Zp2与Zs的关系：

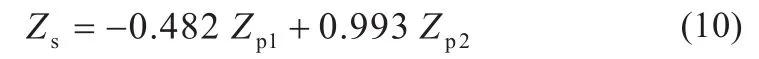
将公式(8)(9)代入(10)，得标准化后的容量与标准化后的4个自变量的关系为：

将所有变量还原到非标准化的原始变量，得到最终的SOH估计模型公式为：

式中：x1～x4分别对应2.1中的特征参数。

在不同初始SOC下，基于PCA的回归模型的拟合系数如表3所示。

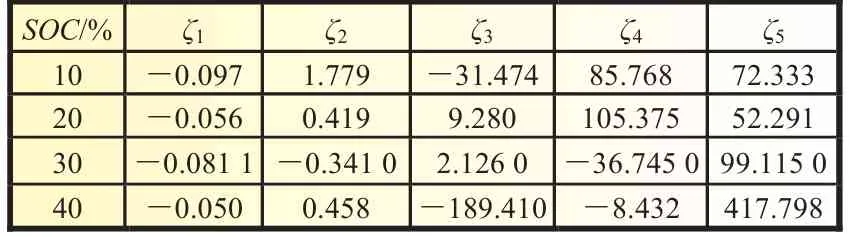
表3 不同初始SOC下估计模型的拟合系数

3 结果与分析

为了验证所提算法的鲁棒性，选取SOH分别为92.16%、86.38%和83.26%的3块样本电池A、B和C在初始SOC分别为10%、20%、30%和40%进行算法验证，其估计值和真实值对比结果如表4所示。

表4 算法估计与真实值的结果对比 %

从表4可以看出，在不同初始SOC下所提算法均能获得2%以内的SOH绝对相对估计误差，其中最大误差为1.10%，最小误差为0.02%，分别在初始SOC为10%和30%下，样品A和B的估计误差。在初始SOC为10%下样品A、B、C的估计误差分别为1.10%、0.62%和0.09%；在初始SOC为20%下样品A、B、C的估计误差分别为0.44%、0.07%和0.64%；在初始SOC为30%下样品A、B、C的估计误差分别为0.54%、0.02%和0.33%。

为了进一步验证所提算法在初始SOC误差下的鲁棒性，选取样本电池A、B、C进行初始SOC为30%且偏差为±5%条件下的算法验证，其算法估计值和真实值的结果对比如图4所示。

图4中，实心和空心圆圈分别代表+5%偏差估计和误差值，实心和空心三角分别代表-5%偏差估计和误差值，*代表真实值。样品A在+5%偏差下SOH估计误差最大，为3.65%，其在-5%偏差下SOH估计误差最小，为0.95%。样品B在+5%偏差下的SOH估计误差均在3%左右，样品C在+5%偏差下的估计误差为1.21%，在-5%偏差下的估计误差为3.12%。因此，在±5%的初始SOC偏差下，所提算法的SOH估计精度能保持在4%以内，说明在驾驶员的不明确充电意图下仅需要少量数据就能实现SOH快速估算。而且不同成分电池的dQ/dV曲线各峰的位置和面积是由相变电位和反应锂离子数量决定的，即电压曲线平台区的位置和高度。随电池老化的电压曲线变化被量化为某段SOC区间内电压平台区的偏移量。因此针对不同成分的电池，该方法仍然适用。

图4 初始SOC偏差±5%下的SOH估计结果

4 结束语

文中提出了一种基于电压偏移序列的电池健康状态估计方法，该方法以不同SOH下的充电数据为基础，构建不同SOC区间的电压偏移序列，并采用PCA法提取分布特征参数，进行回归建模。实验结果表明：利用基于电压偏移序列对电池SOH进行预测，在不同初始SOC下的最大误差仅为1.10%，并进一步验证其在初始SOC误差±5%下的鲁棒性，电池SOH估算误差仍能保持在4%以内。该方法能用于多种类型的电池，并能够在考虑驾驶员的充电意图下仅需少量历史数据进行快速SOH估算，对提高系统计算效率、降低成本具有重要意义。