基于SOM-K-means算法的番茄果实识别与定位方法

李 寒 陶涵虓 崔立昊 刘大为 孙建桐 张 漫

(1.中国农业大学现代精细农业系统集成研究教育部重点实验室， 北京 100083;2.中国农业大学农业农村部农业信息获取技术重点实验室， 北京 100083)

0 引言

在农业生产中，由于果实的状态存在差异性、局部植株样貌存在复杂性[1-2]，因此目前绝大多数采摘工作由人工完成。为了节约成本、提高采摘效率，采摘机器人已广泛使用，机器人自动采摘时对果实的准确识别已成为研究热点[3-4]。自动采摘一般分为果实识别、定位、采摘，果实识别和定位的准确与否对采摘结果至关重要。

基于果实二维图像信息，孙建桐等[5]提出一种基于几何形态学和迭代随机圆相结合的目标提取算法，以分割粘连番茄果实。李寒等[6]提出，对粘连或被遮挡的番茄果实采用局部极大值法和随机圆环变化检测圆算法进行目标提取，再使用SURF算法进行目标匹配。SI等[7]提出通过立体匹配和随机环算法进行苹果果实定位。由于没有结合果实的深度信息，这些方法对于复杂自然环境下粘连或被遮挡的果实识别效果有限。MEHTA等[8]提出通过多个相机得到伪立体视觉，进而对番茄进行定位，虽然引入了立体视觉，但是需要多个相机，成本较高，算法也较为复杂。

随着科学技术的发展，RGB-D相机(可以独立获取彩色图像和深度图像的相机)的出现为解决该问题提供了思路[9-10]。虽然已经有大量研究成果[11-14]，但其正确识别率和识别速度还不能满足大批量采摘的要求。

根据采摘机器人对果实进行识别和定位的要求，需要研究一种快速、准确的重叠果实分割方法[15-17]。聚类方法在图像分割中的应用有很多研究成果。聚类(Clustering)方法可分为划分法、层次法、密度法、网格法、模型法等。自组织映射(Self-organizing map，SOM)算法在聚类模型法中较有代表性，它可以通过自身训练，自动对输入模式进行聚类，具有简明性和实用性[18-19]。K-means算法在划分法中有代表性，具有设计简单、收敛快速、聚类有效的特点[20-22]。

本文以番茄为研究对象，使用ZED相机采集图像，综合颜色信息和深度点云信息，对番茄果实的识别、分割和定位进行研究，将SOM神经网络和K-means算法相结合，提出一种基于RGB-D图像和K-means优化的SOM算法(SOM-K-means)的番茄果实识别与分割方法，以解决因番茄果实粘连、遮挡而造成的图像难以分割的问题。

1 材料与方法

1.1 试验材料与设备

试验所用番茄图像拍摄于中国农业科学院番茄种植大棚内。拍摄时间2019年1月3日15:00—16:30和2019年1月8日14:00—16:00，光线良好，试验图像如图1所示，并用游标卡尺对每个番茄的实际半径进行测量。大棚内所种番茄果实品种是实验品种，果实大小适中且多处存在番茄重叠现象。番茄是否成熟由有经验的番茄采摘人员确认。

使用Stereolabs公司生产的ZED相机采集图像，该相机为双目相机，可以获取图像的深度信息。在Windows平台上，通过Visual Studio 2015将ZED相机与OpenCV库以Cmake为编译器进行结合，成功实现了对图像三维信息的处理。

1.2 果实识别与定位方法

果实识别与定位方法包括3个步骤：RGB图像预处理；深度点云处理；点云数据聚类及果实轮廓拟合。具体流程如图2所示。

1.2.1RGB图像预处理

考虑到番茄果实颜色与周围种植环境的显著差异，将采集到的RGB位图进行转换，运用HSV空间对番茄进行处理，其中H、S、V分别表示图像的色调、饱和度和亮度。首先对图像的亮度分量V进行脉冲噪声判断，若存在噪声则对图像进行滤波增强处理。通过反复试验，获得成熟番茄果实的H、S、V分量的灰度取值范围，对不在该范围里的点进行过滤，再经过二值化得到将番茄果实与其他物体分开的二值图像。关于阈值的选取，由于实际果实检测时是实时拍摄，使用自适应取值会导致延迟较长，不利于实际采摘。所以本文方法以番茄果实是否成熟为界限，经数据分析和测试，设定H、S、V分量的灰度范围分别为0～20、170～180，110～255，46～255，从而对图像进行分割，剔除灰度范围外的部分，实现成熟番茄果实的分割。对二值图像进行分割，利用形态学闭运算去掉内部轮廓、小轮廓以降低误识别率。但由于在实际采摘过程中，番茄会出现叶子遮挡、粘连的情况，因此还需要根据图像的深度信息对不同番茄果实进行分离。

1.2.2深度点云处理

ZED相机提供了双目立体视觉的功能，因此可以生成图像的深度图，如图3所示。ZED相机可以检测的有效范围是0.3～5 m。较浅的颜色表示距离较小；较深的颜色表示距离较大。完全黑色的点表示检测距离超出了ZED相机的有效检测范围。这些点的深度是非数字的，被滤除。

在图3中，不同颜色轮廓上点的深度差大于同一个番茄果实轮廓上点的深度差的最大值，表明这些点属于不同的番茄果实轮廓。

使用ZED相机获取图像分割信息的同时也可以获得轮廓矢量信息。轮廓矢量中的每个元素都是一个点结构。在深度图中读取每个点的三维坐标信息；之后遍历这些点，通过ZED相机自带的getValue函数对图像进行三维重建，将世界坐标系转换为相机坐标系进而得到点云中的点在相机坐标下的三维坐标信息。通过输入输出流把点云的三维坐标信息导入到本地文件中并具体分为二维坐标和深度信息。考虑到ZED相机识别距离范围的局限性，为了提高SOM神经网络聚类的准确性，在获取数据文件后，对数据进行过滤，通过密度聚类对具有高分散性的点进行滤波，以获得精度更高的点。

1.2.3点云数据聚类及果实轮廓拟合

本文用K-means算法对SOM算法进行优化，提出SOM-K-means聚类算法。将已获取的点云数据进行处理后，使用SOM-K-means算法对其进行聚类，进一步得到识别和定位结果。

(1)SOM算法

SOM算法是一种聚类和高维可视化的无监督学习算法。SOM 神经网络是一种非监督、自适应、自组织的网络，它由输入层与输出层(也叫作竞争层)组成，输出层中的一个节点代表一个需要聚成的类。训练时采用“竞争学习”的方式，每个输入的样例在输出层中找到一个和它最相似的节点，称为激活节点。接着对激活节点的参数进行更新，同时，和激活节点临近的点也根据它们距激活节点的距离适当更新参数。

设输入样本为X=(x1,x2, …,xn)，是一个n维向量，则输入层由n个输入神经元组成；输出层Wi=(wi1,wi2, …,win)，1≤i≤m，有m个权值向量，则输出层由m个输出神经元组成。输入层与输出层中的神经元互相连接，其结构如图4所示。

SOM算法的步骤如下：①初始化，设定网络的权值、学习率初值、邻域半径以及学习次数。权值使用较小的随机值进行初始化，并对输入向量和权值做归一化处理

X′=X/‖X‖

(1)

W′i=Wi/‖Wi‖

(2)

式中X′——进行归一化处理后的输入向量

W′i——进行归一化处理后的权值向量

②采样并随机选取输入量，将数据集中的样本输入到神经网络中。③样本与权值向量做点积，进行竞争，点积值最大的输出神经元记为该样本的获胜神经元。④对权值进行更新，对获胜的神经元及其拓扑邻域内的神经元的权值进行更新。

W(t+1)=W(t)+η(t,d)(X-W(t))

(3)

其中

η(t,d)=η(t)e-d

(4)

式中t——训练时间

d——获胜神经元的拓扑距离

η——学习率，是关于t与d的函数

W(t)——更新前的权值

其中，η(t)一般取迭代次数的倒数。⑤更新学习率η及拓扑邻域N, 其中，N随时间增大距离变小。⑥判断模型是否收敛，如果学习率η≤ηmin或达到预设的迭代次数，结束算法，否则跳转到步骤②。

该算法的优点是无需监督，无需提前告知分类数便能自动对输入模式进行聚类，容错性强，对异常值和噪声不敏感。其缺点是在训练数据时会出现有些神经元始终不能胜出，导致分类结果不准确；SOM网络收敛时间较长，运算效率较低。

(2)K-means算法

K-means算法采用距离作为相似性的评价指标，即数据对象间的距离越小，则它们的相似性越高，越有可能为同一个类簇，并把得到紧凑且独立的簇作为最终目标。

K-means算法步骤如下：①从数据集中随机选取k个数据对象作为k个簇的初始聚类中心点。②计算剩余每个数据对象与各个簇的聚类中心之间的距离，并把每个数据对象归到距离它最近的聚类中心的类。③更新每个簇的聚类中心，即根据聚类中现有的对象重新计算每个簇的聚类中心，以各个簇内所有对象的平均值作为新的聚类中心。④重复步骤②、③直至新的聚类中心与原聚类中心相等或小于指定阈值，算法结束。

该算法的优点是算法快速、简单，收敛速度快；缺点是初始聚类中心的设定对于聚类结果影响较大；聚类种数k需要预先给定，而在很多情况下k的估计是非常困难的。

(3)SOM-K-means算法

基于SOM算法和K-means 算法的步骤以及各自的优劣，本研究将二者结合，对SOM算法进行优化。由于SOM算法无需提前告知分类数便能自动对输入模式进行聚类，但在训练数据时可能出现有些神经元始终不能胜出，导致分类结果不准确，且网络收敛时间较长；而K-means算法的优点便是收敛速度快，但初始聚类中心和k的大小很难提前确定。因此，本文提出SOM-K-means算法，即SOM的优化算法，将SOM与K-means算法结合，既解决了K-means算法中初始聚类中心和k的设定问题，又克服了SOM算法中网络收敛较慢、分类结果不准确的缺陷。

SOM-K-means算法步骤如下：①将数据集输入到SOM神经网络中进行聚类，输出分类种数以及初步分类结果。②将步骤①中得到的分类种数作为k值，分类结果中每一类中随机取一个数据对象作为初始聚类中心，执行K-means算法进行聚类并得到最终结果。

本文算法在保持 SOM 网络自组织特性的同时，创新性地将SOM算法和K-means算法相结合，融合了SOM和K-means算法的优点，又弥补了两种算法的缺陷，在分类结果的准确度和运算效率上都有了较大的提高。SOM-K-means算法的流程图如图5所示。

1.2.4算法性能评价

经上述操作后能得到番茄识别结果，进而对识别和定位结果进行分析。本试验通过正确识别番茄个数与图中实际番茄数是否相等来评价识别结果；通过果实实际半径与拟合轮廓半径比较来对果实定位精度进行评价。

在结果分析中，首先将图像的相机坐标系转换为世界坐标系，以便与真实值进行比较，进而对识别结果和定位精度进行评价。

对于识别结果的评价，统计图像中实际番茄个数、算法识别番茄个数、算法漏识别番茄个数、正确识别番茄个数、错误识别番茄个数。输出结果中，黄色的圆为算法识别的番茄轮廓，算法识别番茄个数即为图中黄色圆的个数，正确识别番茄个数即为图中黄色圆本身与实际番茄果实半径和圆心误差分别不超过5.00 mm和3.00 mm的黄色圆个数，错误识别番茄个数即为图中黄色圆本身与实际番茄果实半径和圆心误差分别大于5.00 mm和3.00 mm的黄色圆个数。由正确识别的番茄个数占实际番茄个数的比例计算出识别的正确率。

对于定位精度的验证，随机抽取结果图的部分样本，通过比较实际番茄半径和拟合轮廓半径，计算出识别结果的均方根误差、平均偏差、平均相对误差。

2 试验结果与分析

从采集的图像中随机选取80幅作为样本，每幅图像根据番茄果实的数量和尺寸可以得到600～2 000个信息点。使用SOM-K-means算法对其处理之后，统计识别结果的混淆矩阵来对该方法进行评估。通过统计和计算得到试验的准确率、精确率、灵敏度、特异度4个指标值，并对该算法的可靠性进行分析。

2.1 图像处理与数据采集

图像预处理过程中的中间图像如图6所示。

对捕获的图像进行预处理，获得分割的番茄轮廓点云。从原始图像及其深度图获得点云的3D信息。经过三维重建后，真实世界点云的信息通过C++中的输入和输出保存到创建的试验文件中。

在试验中发现实际拍摄过程中，点云信息中会有一些误判的点，这种点一般比较离散。选取最小轮廓的点数为30，运用密度聚类方法，把偏离密集区域的点去掉，提高点云矩阵信息的容错性和正确率。

2.2 SOM-K-means算法识别结果

执行SOM-K-means算法后，果实轮廓点云的聚类结果如图7所示。图中每个点表示轮廓上的一个点，纵坐标是深度，横坐标表示二维信息。由图7可知，该算法共识别出3个番茄果实。

利用最小二乘法分别拟合出各类点所属的圆，结果如图8所示。在图8中，有3个成熟的番茄果实。将相机坐标系转换为世界坐标系，并通过测量和计算得到拟合圆与对应番茄果实的半径和圆心误差均小于误差阈值，即3个番茄果实均识别正确。另外，由于番茄果实轮廓并不是完全的圆形，因此拟合的圆与果实实际轮廓有一定的误差。

2.3 结果统计与验证

对80幅样本图像进行预处理，执行SOM-K-means算法并输出结果，统计图像中实际番茄个数、算法识别番茄个数、算法漏识别番茄个数、正确识别番茄个数、错误识别番茄个数，并对识别结果进行分析。以图8为例，根据1.2.4节的评价指标，图中实际番茄果实个数为3个，算法识别番茄果实个数为3个，算法漏识别番茄果实个数为0个，正确识别番茄果实的个数为3个，错误识别番茄果实的个数为0个。

此外，试验中的80幅图像样本包含了不同自然环境下的番茄果实图像，图9为部分图像的果实识别和定位结果。从图中可以看出，本文算法对于有叶子遮挡的多个粘连番茄果实、有未成熟番茄遮挡的多个成熟番茄果实、较暗环境下的重叠番茄果实、较强光照下的重叠番茄果实均具有较强的鲁棒性。

对80幅图像样本的识别结果进行统计和计算，得到试验的识别率、漏识别率、正确识别率和错误识别率如表1所示，识别率为92.0%，正确识别率为87.2%。

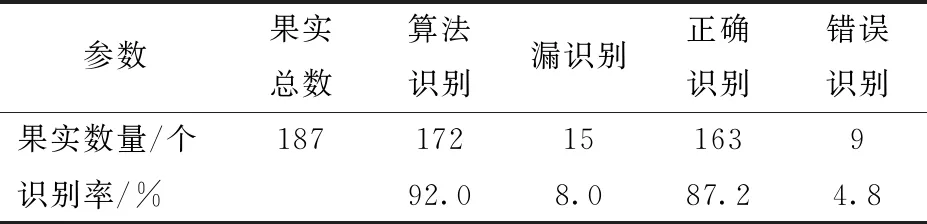
表1 果实识别结果Tab.1 Fruit recognition results

随机选择15幅图像以测试定位精度。表2为番茄果实拟合轮廓半径、实际测量半径、偏差和相对误差。拟合轮廓半径为图中拟合圆的半径，实际测量半径为用游标卡尺手动测量的番茄果实半径，单位均为mm，精度均为0.01 mm。识别结果的均方根误差(RMSE)为1.66 mm，平均相对误差为3.95%。

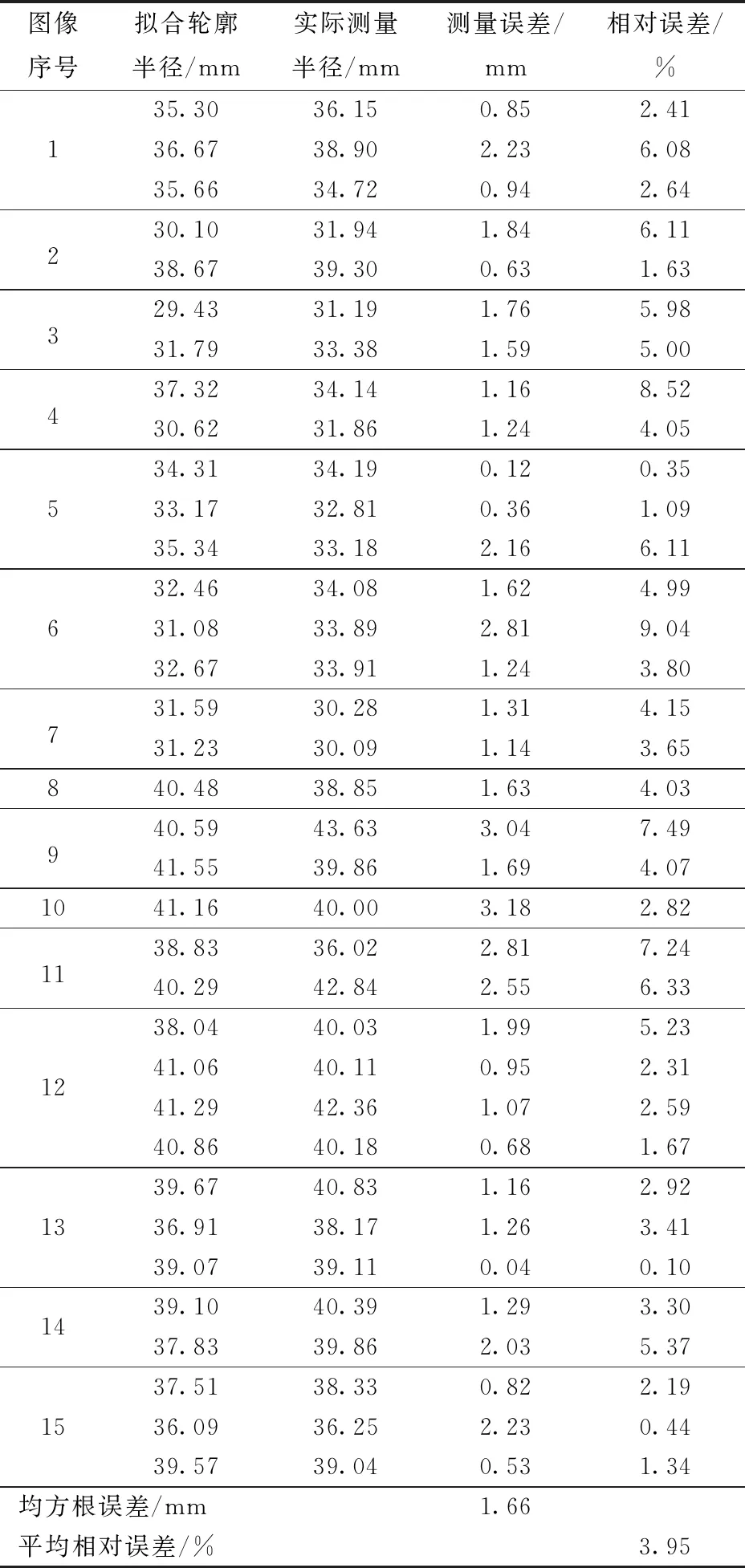
表2 番茄果实实际测量半径与拟合轮廓半径Tab.2 Actual measured radius and fitted contour radius of tomato fruit

3 对比试验与分析

为进一步验证本文方法的性能，加入对比试验，将其与在二维图像上利用Hough变换进行果实识别的传统方法进行比较。

选取与上述试验相同的图像样本，采用在二维图像上利用Hough变换进行果实识别，将其识别结果与本文方法进行对比。对比试验中，根据采集的输入图像对Hough变换进行了改进：修改CIRCLE_HOUGHPEAKS函数中的Threshold变量，改成对圆投票数矩阵最大值的0.99倍，相当于取最大值投票数99%的圆心和半径。由此得到的识别结果如表3所示。

表3 对比试验的番茄果实识别结果Tab.3 Tomato fruit recognition results of comparative experiments

由对比试验结果可知，采用二维平面上的霍夫圆方法对果实进行识别的正确识别率为69.0%，比本文方法低了18.2个百分点。因此，在番茄重叠情况比较复杂的情况下，本文方法的性能相较在二维平面上利用Hough变换的方法有了明显的提升。

结合试验过程和结果，将两种方法进行对比分析。在二维图像上利用Hough变换的方法需要提前输入的参数较多，包括番茄果实个数和半径范围，以及设置参数投票矩阵阈值，选取投票率高的圆心和半径；且其在识别过程中对于图像中干扰项的处理能力不强，导致在非番茄区域也出现了很多圆，从而有相当一部分的投票从番茄区域流失，增加了错误率。本文方法则首先对图像进行预处理，通过颜色、亮度等信息能够很好地识别番茄区域，然后利用果实轮廓的三维信息进行聚类从而识别到重叠番茄，其中深度信息的获取对于识别和定位重叠番茄尤为重要。因此本文提出方法的正确识别率较高，且在比较复杂的情况下具有较强的鲁棒性。

4 结论

(1)针对重叠番茄果实难以分割与识别的问题，提出一种基于RGB-D图像与改进的SOM-K-means算法的番茄果实识别方法。在二维图像的基础上，提取轮廓点的深度信息进行三维聚类；聚类时结合SOM算法和K-means算法的优点对SOM算法进行优化，提出改进的SOM-K-means算法，有效提高了运算效率和果实识别的综合性能。经过大量试验，得出本文方法的正确识别率为87.2%。

(2)RGB-D相机对成熟番茄果实的定位结果均方根误差(RMSE)为1.66 mm，平均相对误差为3.95%，基本满足采摘机器人的要求。

(3)本试验综合轮廓的深度信息，通过聚类将重叠果实的轮廓分开，然后分别进行圆拟合，在番茄果实识别定位方面，比传统的在二维平面上利用Hough变换进行果实识别定位的方法具有更高的准确性和更强的鲁棒性。