美国加州Ridgecrest 地震的地震动特性分析

张琪，陈希†，郑向远

（1.清华大学 土木工程系，北京 100084；2.清华大学 深圳国际研究生院，广东 深圳 518055）

基于地震动工程特性，选取适当的地震动进行结构物的动力响应分析，对于土木工程结构抗震设计和安全评估具有重要意义.目前世界范围内各地震活跃国家或地区正逐渐建立起覆盖整个区域的强震观测台网，这些观测台网的布设为地震动研究提供了丰富的数据来源.长期以来，地震动的研究主要集中在研究地震动三要素（峰值加速度、反应谱和持时）等时频域工程特性，以及基于地震动数据研究不同场地条件下的地震动衰减关系等.

近年来，基于实际地震动数据，冀昆等人[1]结合震害调查，对云南鲁甸MS6.5 地震从幅值特征、衰减关系等方面对地震动参数加以分析.在此基础上，戴嘉伟等[2]将云南鲁甸MS6.5 和云南景谷MS6.6 地震进行对比，发现鲁甸地震地震动参数衰减快于景谷地震，该现象可能与Q 值（介质品质因子）的区域差异性相关.王恒知等[3]采用H/V 单台谱比法分析了地震的场地放大效应，表明台站场地对地震动存在明显的放大现象.夏坤等[4]对汶川地震部分台站记录进行分析，研究了传播距离和场地条件对远场地震动的影响.国内外多年来涌现出与上述成果类似的研究[5-6]，不一一列出.

2019 年7 月4 日和7 月6 日，在美国加州同一地点相隔不到34 h 相继发生6.4 级和7.1 级强震，是一个较为特殊的事件.这两次强震同属于一个地震断裂带，且震源相近，属于同一个地震序列.因此，对这两个事件的地震动特征及其影响进行梳理和分析研究具有重要意义.本文基于美国工程强震数据中心（CESMD）获取的地震动信息，首先对地震动衰减关系进行研究；其次，鉴于它们震源相近，本文还对比研究了两次地震动PGA、反应谱和持时等时频域特性的差异，并利用希尔伯特-黄变换研究了地震动能量在时-频域的分布特征.

1 数 据

1.1 地震信息

2019 年7 月4 日10 时33 分，美国加利福尼亚州南部科恩县里奇克莱斯特（Ridgecrest）附近发生6.4 级地震，震中位于瑟尔斯谷西南12 km 处，震源深度10.7 km.相隔不到34 h，该地区再次发生强震，震级达7.1 级，震源深度8.0 km，震中与早前发生的6.4 级地震震中十分接近，仅相距17 km.虽然二者震级仅相差0.7 级，但基本上不属于双震型事件.目前一致的看法是，后者为主震，前者为前震[7].事实上，在二者之间还发生过一个5.4 级前震.

这是加州近20 年来破坏性最强的两次地震，均发生在长约45 km、宽约15 km 的利特尔莱克断裂带上，震中附近地表出现大量裂痕及偏移，房屋倒塌，道路损毁，甚至引起火灾等次生灾害，造成1 人死亡，数十人受伤，及超过50 亿美元的较严重经济损失[8-9].图1[10]和图2[11]展示了由7.1 级地震造成的地表开裂和房屋损坏情况.同时，距离震中约300 km的洛杉矶和周边城市以及内华达州拉斯维加斯都有明显震感.

图1 7.1 级地震引起的地表裂痕[10]Fig.1 Surface rupture during the MW 7.1 earthquake[10]

图2 7.1 级地震引起的房屋损坏[11]Fig.2 House damage by the MW 7.1 earthquake[11]

1.2 数据选取

本文中强震动记录数据来源于美国工程强震数据中心（CESMD）.CESMD 自7 月4 日至7 月11 日，包括主震及次大地震（7.1 级和6.4 级）在内，共记录到105 次地震（≥MW3），剔除震源深度小于等于0（可认为是地面塌陷或人为引起的震动）的数据后，得到94 次地震.各地震震中分布如图3 所示.图4所示为各次地震震级随时间变化曲线，从图中可看出，在6.4 级的次大地震和7.1 级的主震之间发生的地震，震级主要集中在MW3～4.5，余震震级主要集中在MW4～5.5.图5 为地震震级与相应的震源深度分布散点图，从图中可知，震源深度主要集中于0～13 km，均属于浅源地震（震源深度小于70 km），因此对地面建筑物带来的破坏较为严重.

图3 各地震的震中位置分布Fig.3 Distribution of the selected earthquake epicenters

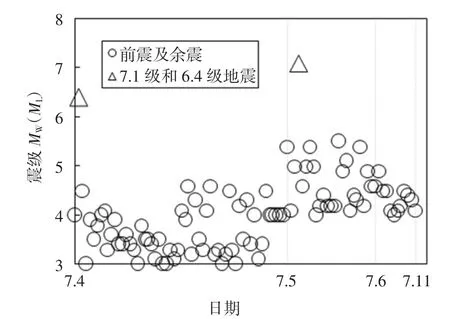
图4 地震震级随日期变化曲线Fig.4 Earthquake magnitude varying with date

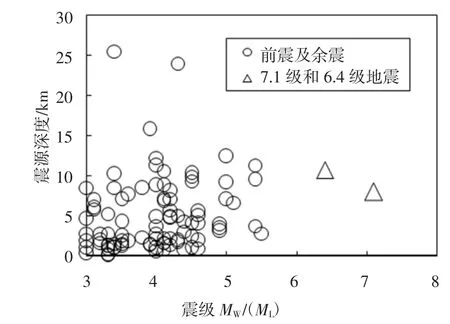
图5 地震震级与相应的震源深度分布Fig.5 Earthquake magnitude with corresponding focal depth

2 衰减关系

6.4级和7.1级地震震级均较大且相差仅0.7级，在同一地震序列中能量较接近，因此以这两次地震动记录为例，进行地震动参数衰减关系的讨论.在给定震级、震中距等条件下，利用地震动参数的衰减曲线能够对地震动进行参数估计，从而用这些估计参数作为结构抗震和安全评估计算的输入[12-15].

鉴于这两次地震在加州的台站均有记录，本文分别选取了两次地震动中峰值加速度（PGA）和峰值速度（PGV）较大的地震动记录，7.1 级地震中选取前49 条水平地震动记录，6.4 级地震中选取前34 条水平地震动记录，并分别与已有模型对比.该模型为俞言祥[16]基于美国西部NGA 强震数据库建立的基岩场地水平衰减关系模型，结果如图6 所示.

图6 地震动衰减模型和测得的PGA 与PGV 对比Fig.6 Seismic ground motion attenuation models versus measured PGA and PGV

从图6 中可看出，对于7.1 级和6.4 级地震的PGA 和PGV 的实际记录值，俞言祥模型曲线基本从这些散点中间穿过.这些记录数据能够较好地反映出PGA 和PGV 随震中距的增大而衰减的趋势.其中，6.4 级地震对应的PGA、PGV 的残差平方和（SSR）均小于7.1 级地震，如表1 所示.这说明该模型对6.4 级地震的地震动参数预测更加准确.此外，值得注意的是，在7.1 级地震中，震中距R=34.5 km的台站CLC，其PGA 和PGV 均远远高于俞言祥模型的预测值，造成此差异的原因有二：1）台站CLC 虽然震中距较大，但是其断层距Rrup=2.8 km 远远小于其余台站，说明该台站与发震断层十分接近，地震波传播路径较短，因而地震动参数较大；2）台站CLC 所处场地条件为C 类（软基岩），不满足俞言祥模型的基岩场地条件，可能存在较大程度的场地放大效应，因而地震动参数较大.

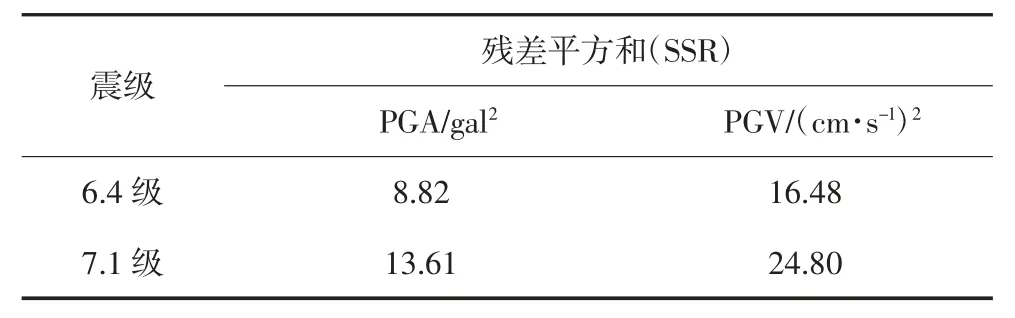
表1 所测地震动衰减参数和俞言祥模型间的残差平方和Tab.1 SSR of measured seismic ground motions against Yu’s attenuation model

3 地震动三要素

为了研究该地震活动中地震动的时频域特性，本文从6.4 级和7.1 级两次较大地震中分别选择了137 条和126 条地震动记录，并按照震中距的大小分为＜100 km，100～200 km 以及＞200 km 三类（见表2），研究两次主要地震中震中距所造成的差异.

表2 地震动记录分类情况Tab.2 Classification of earthquake ground motions

3.1 PGA 和持时

表3 给出了6.4 级和7.1 级地震中不同震中距下水平和竖向地震动峰值加速度（PGA）平均值，同时也给出了竖向和水平PGA 的比值关系.从表3 中可看出在同一次地震中，随着震中距的扩大，无论是水平还是竖向地震动PGA 都减小，这与PGA 随震中距变化的一般规律相同[17].同时，竖向和水平PGA 的比值PGAV/PGAH也随着震中距变大而减小.对于不同震级（MW6.4 vs.7.1）同一震中距分类地震动而言，震级越大则PGA 越大；另外，震级增大时，PGAV/PGAH也会增大.

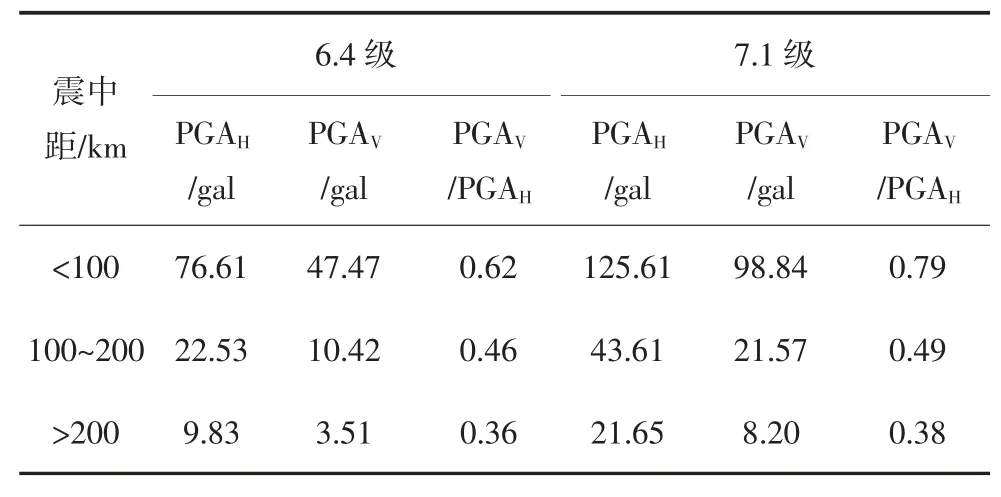
表3 不同震中距下的水平和竖向地震动平均PGATab.3 The horizontal and vertical PGA of seismic recordings with different epicenter distance

表4 列出了6.4 和7.1 级地震中不同震中距下水平和竖向地震动持时的平均值.本文采用90%能量持时[18-20]来确定地震动持续时间（一般又称为强震持时），是由于这种方法能够更充分地反映地震动的原始特征.该持时定义为地震动能量从总能量的5%累积到95%所经历的时间，见式（1）和式（2）.

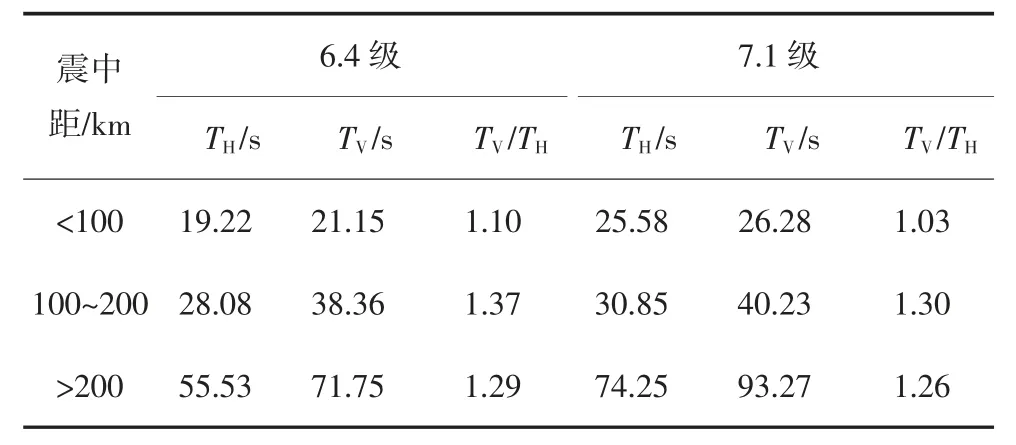
表4 不同震中距下的水平和竖向地震动平均持时Tab.4 The averaged horizontal and vertical duration of seismic recordings with different epicenter distance

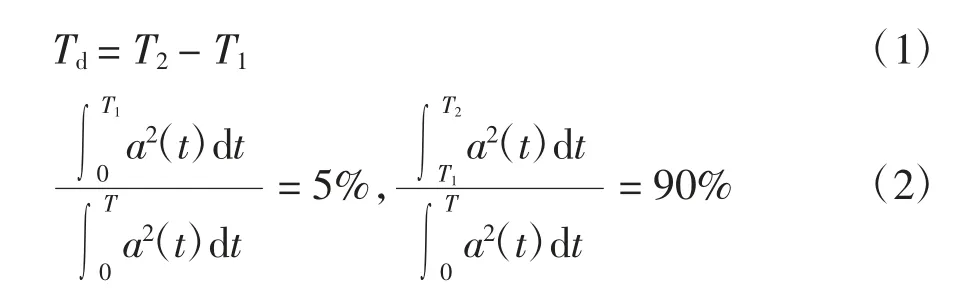
式中：T 为总持时，其分为3 段，分别是0～T1，T1～T2和T2～T，T1、T2分别是总能量的5%和95%所对应的时间点，Td表示90%能量持时.从表4 中可以看出，随着震中距增加，地震动加速度持时也相应增加，尤其在震中距大于200 km 时，无论是水平向还是竖向地震动，加速度持时增幅最大.另外，对于竖向和水平持时比值TV/TH，震中距在100～200 km 内最大，震中距小于100 km 最小.值得注意的是，与PGA 水平和竖向数值大小关系不同的是，对于地震动90%能量持时而言，竖向持时始终大于水平向持时.不同的震级也会影响持时大小，在本地震事件中，震级大地震动持时也变大，但是TV/TH却略有减小.

3.2 反应谱

利用精确法计算地震动的5%阻尼比加速度反应谱[21-22]，并将所有反应谱归一化处理，计算每一类别的平均反应谱，从而对比研究其差异.

图7（a）（b）分别表示两次地震中不同震中距类别的水平和竖向地震动加速度反应谱，纵坐标β 为归一化的加速度反应谱值.从图中可看出，无论是水平还是竖向反应谱，对于同一次地震（6.4 级或者7.1级），随着震中距增大，其谱值向长周期偏移，对于震中距超过200 km 的地震动反应谱，其特征周期超过0.8 s，这反映出地震动传播距离越远，高频部分被削弱越多，而低频成分则不断扩大.另外，对于同一震中距分类，不同震级的2 条反应谱的差别较小，尤其是对应第一类和第二类震中距（皆小于200 km）的地震动.造成如此结果的原因是这两次地震属于同一个地震序列，同时两次地震震源相近.

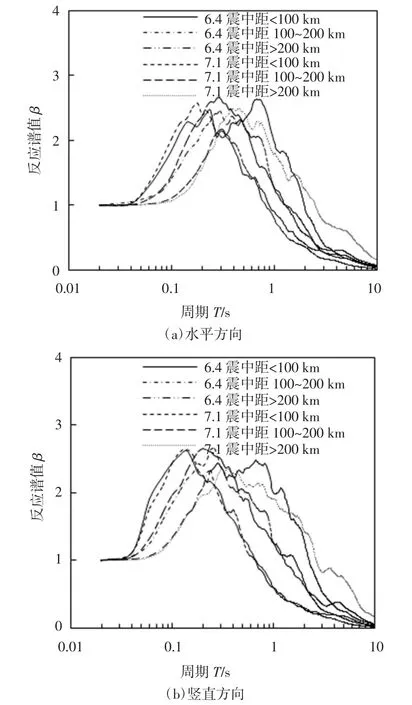
图7 两次地震中不同震中距下的平均地震动反应谱对比Fig.7 Comparison of averaged seismic response spectra in the two earthquake events by epicenter distances

为了对比7.1 级和6.4 级地震中最显著反应谱的差别，本文选择了获取的所有地震动数据中7.1 级地震PGA 最大的地震动，以及对应于该地震动观测台站记录得到的6.4 级地震的地震动数据，分别为R1 和R2，具体信息见表5.图8（a）（b）分别表示R1和R2 的水平和竖向地震动反应谱（β 为归一化的加速度反应谱值）.对于水平方向的反应谱，在周期0.2 s ＜T ＜0.5 s 时，R1 反应谱值显著大于R2，因此考虑到7.1 级地震在6.4 级之后发生，如果在此场地上的结构经受6.4 级地震的地震动荷载后产生结构损伤，自振周期变长，在此情况下遭受7.1 级地震，结构会受到更加严重的破坏.此外，从竖直方向的反应谱也可看出，R1 的反应谱峰值要大于R2.

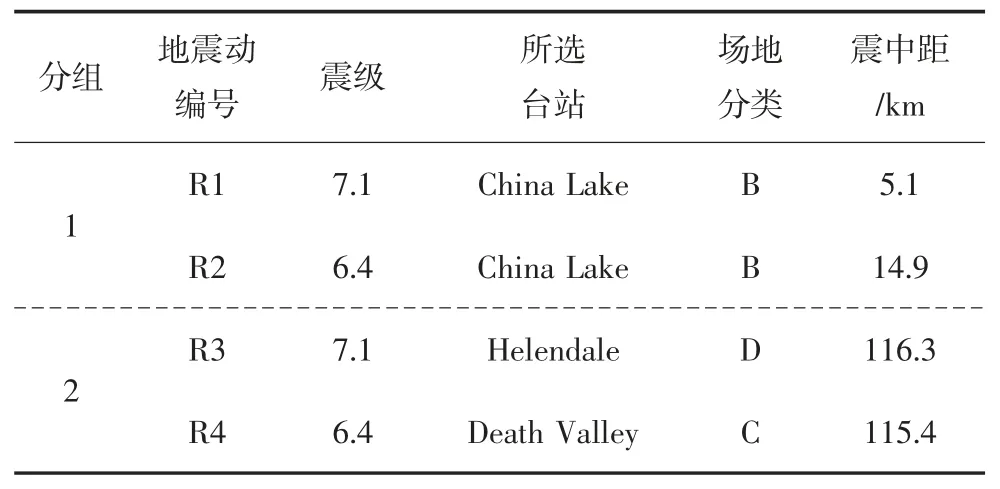
表5 选取的地震动信息Tab.5 The selected seismic recordings

图8 R1 和R2 地震动反应谱对比Fig.8 Comparison of response spectra of R1 and R2

图9（a）（b）分别给出了7.1 级和6.4 级地震中水平地震动反应谱峰值所对应的周期（下称峰值周期）在不同范围的分布图.除了图9（a）中最后一个柱形代表周期大于1.8 s 的数据量，其他直方柱的周期间隔都是0.2 s.直方柱的高度表示峰值周期落在某一周期范围内的地震动数量，直方柱顶端数据表示落在此周期范围内的各地震动反应谱峰值的平均值.从图中可看出，无论是7.1 级还是6.4 级地震，两者大部分地震动峰值所对应的周期都落在0.2～0.4 Hz，在此周期内，7.1 级地震的地震动平均反应谱峰值为3.75，比6.4 级的平均反应谱峰值3.61 略大.另外两个差别是，对于6.4 级地震，落在0.6～0.8 s 范围内的地震动反应谱峰值个数超过30 次，明显多于7.1 级地震的地震动；对于7.1 级地震的地震动，存在3 条峰值周期大于1.8 s 的较长周期地震动，而6.4 级地震则没有.

4 HHT 谱分析

4.1 希尔伯特-黄变换

针对地震动频域特征所采用的方法一般是傅里叶变换[23]，它更适用于平稳随机过程，即假设频率不随时间变化.然而实际中地震动记录的幅值和频率成分不断随时间变化，在严格意义上是一个非平稳随机过程[24]，传统的傅里叶变换方法无法对地震动特性进行精细化研究.为了较好地描述地震动从开始激发到强震段，然后衰减结束的全过程，本文采用希尔伯特-黄变换（HHT）[25-26]，研究地震动能量在时间和频率成分中的分布情况.

为了利用HHT 谱对7.1 级和6.4 级地震动进行特征分析，本文从收集的地震动数据库中选择了2组数据进行研究.每组中共2 条地震动，其中第一组中一条是7.1 级地震中记录到的最大水平地震动，该条地震动由“China Lake”地震台站记录得到，编号记为R1，另一条是该强震观测台站所获取的6.4 级地震的水平地震动，编号记为R2，该组数据可以用来对比不同震级对地震动造成的影响差异.由于该组地震动是两次地震中分别记录的最大和次最大地震动，研究它们的差异是很有意义的.第二组是为了对比不同场地条件地震动HHT 谱的差异，包含了7.1级和6.4 级地震中不同台站获取的水平地震动数据，它们对应的震中距分别是116.3 km 和115.4 km，十分接近，编号分别记为R3 和R4，具体信息见表5.

4.2 HHT 谱

4.2.1 第一组

图10（a）分别给出了第一组中7.1 级和6.4 级地震中记录的两条地震动R1 和R2 的时程和HHT 谱.由于这两条地震动都是从同一个强震观测台站获取的，因此它们所在的场地条件是相同的，属于B 类场地，不同的是震级以及震中距的差别.从图中可看出，R1 的PGA 为466.28 gal，而R2 的为184.95 gal，这主要是因为R1 的震级比R2 的震级大所致，而且震中距明显偏小.另外，R1 的能量持时也比R2 的大，分别是15.14 s 和11.52 s.

图10（b）（c）反映了R1 和R2 的能量在时间和频率上的分布情况.其中，R1 的HHT 谱中显示最大瞬时能量为442.7 gal2，所对应的瞬时频率为5.06 Hz，发生在地震动时程的第15.6 s.R2 的HHT 谱中最大瞬时能量为209.2 gal2，比R1 最大瞬时能量小很多，这也体现在两者的PGA 的大小上，其所对应的瞬时频率为7.21 Hz，大于R1 的瞬时频率.由此可见，该台站所记录的7.1 级地震的地震动与6.4 级地震动相比，主要能量偏向于更低频成分.考虑到7.1级地震在6.4 级之后，这会对结构造成更严重的破坏，这与针对它们反应谱的分析结果一致.

由于通常情况下针对地震动特性的讨论是利用传统傅里叶变换进行频域分析，本文同样用该方法计算了地震动的卓越频率，即地震动功率谱中最大谱值对应的频率.另外，进一步在时程上计算了各地震动PGA 所在那个循环的峰-谷频率，具体结果见表6.从表6 中可看出，卓越频率是三者中最低的，而峰-谷频率更接近于HHT 瞬时频率.

图10 第一分组中地震动及其HHT 谱（R1 和R2）Fig.10 The selected horizontal recordings and the corresponding HHT spectra from Pair 1（R1 和R2）

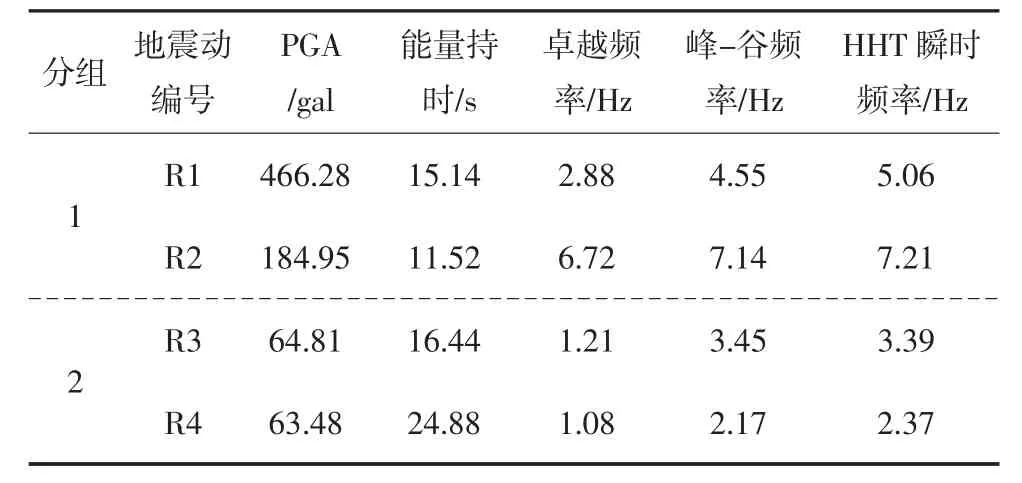
表6 选取的地震动计算结果Tab.6 The selected seismic recordings and their statistics

4.2.2 第二组

图11（a）给出了第二组中7.1 级和6.4 级地震中记录的两条地震动R3 和R4 的时程和HHT 谱.这两条地震动对应的震中距分别为116.3 km 和115.4 km，基本一致，而强震观测台站所在场地分类不同，分别是D 类和C 类场地.从图中可看出，R3 的PGA为64.81 gal，R4 为63.48 gal，两者的PGA 基本相同，但是考虑到R3 和R4 的震级不同，一般来说，震级越大则PGA 越大，如第一组地震动数据一样，但是这一组地震动PGA 却十分接近，主要原因在于其场地条件的差异.

图11（b）（c）是R3 和R4 的HHT 谱.其中，R3的HHT 谱中显示最大瞬时能量为62.36 gal2，所对应的瞬时频率为3.39 Hz，而R3 的卓越频率为1.21 Hz，峰-谷频率为3.45 Hz，故而与第一组数据类似，峰-谷频率和HHT 谱中最大能量对应的瞬时频率更加接近，而卓越频率是三者中最小的.R4 的HHT 谱中最大瞬时能量为55.28 gal2，略小于R3，与PGA 的大小关系一致，其所对应的瞬时频率为2.37 Hz，小于R1 的瞬时频率.其卓越频率、峰-谷频率和HHT谱瞬时频率的关系与R3 一致，见表6.

图11 第二分组中地震动及其HHT 谱（R3 和R4）Fig.11 The selected horizontal recordings and the corresponding HHT spectra from Pair 2（R3 and R4）

5 结论

近期美国加州Ridgecrest 发生的较大地震中，同一地震序列中存在6.4 级和7.1 级两次较大震级的地震活动，且两者的发生时间及震源较接近，本文分别收集了二者的地震动记录，研究它们相应的地震动特性，得到以下主要结论：

1）两场地震中所选地震动的PGA、PGV 的衰减趋势与俞言祥模型吻合较好，其中6.4 级地震的地震动参数与模型的吻合度更高.PGA 和PGV 大致随震中距的增大而衰减，但是断层距和场地条件的差异也可能造成PGA 和PGV 数值的异常.另外，地震动的能量持时随震中距和震级的增大而增大，同一观测台站记录的竖向地震动能量持时大于水平向持时.对于同一次地震，随着震中距增大，其反应谱值向长周期偏移.同一地震序列中的两次地震（如本文6.4级和7.1 级），它们的反应谱基本相似，尤其是在震中距小于200 km 的情况下.

2）HHT 变换可以获得地震动的HHT 谱，从而用来分析地震动能量在时间和频率上的分布情况.从频率成分来看，地震动HHT 谱最大能量所对应的瞬时频率和地震动时程PGA 所在循环的峰-谷频率很接近，卓越频率明显小于HHT 瞬时频率和峰-谷频率.由于两次地震的震中和发震时间比较接近，因此两次地震中地震动的时-频特性基本相似.但也注意到，二者存在着差异，比如在震中的相同场地条件下，7.1 级地震中所测记录（R1）的卓越频率和HHT瞬时频率都明显小于6.4 级地震的记录（R2），因而对所处区域内的结构的动力响应自然也造成不同程度的影响.

3）通过对上述地震动分析可知，结构若经历6.4级地震之后产生损伤，其自振周期会变长，如果再次遭受主要能量更偏向长周期成分的7.1 级地震的地震动作用，就可能会对结构造成更为严重的破坏.这将通过后续的具体震害调查予以进一步确认和深入分析.