虚位移原理在求解梁式杆件内力方程中的应用
何燕青,吴佳俊,李湘岳,张飘阳,朱兵见
(台州学院 建筑工程学院,浙江 台州 318000)
0 引言
虚位移原理又称为虚功原理,虚功是指力在虚位移中所做的功。虚位移原理是分析静力平衡问题的主要方法之一,广泛应用于未知力和未知位移的求解,尤其在结构力学中,在其基础上推导而来的积分法和图乘法使得位移计算量较之材料力学方法大大减小。同时虚位移原理也是分析动力学的重要基础,它为人们求解平衡问题提供了一个极佳的工具,在经典力学中起着支撑作用[1]。
在材料力学中,梁的内力主要包括轴力、剪力和弯矩。计算梁的内力的方法主要是截面法,这一解题方法计算量大,且一般需要求出支座约束反力。如果利用虚位移原理进行求解,则不需要求出支座约束反力,就能够求解任意截面的弯矩与剪力,这一方法不失为对内力方程求解的有用补充。
1 虚位移原理的概念及应用
1.1 虚位移原理的概念
设一质点系具有理想约束,其中某质点受力如图1所示。FNi的虚功之和为零,其平衡的充要条件是:作用于质点系的所有主动力在任何虚位移上所做虚功的和等于零[2],表达式如下:

其中,Fi是作用在质点上的主动力,δγi是该质点上给定的虚位移,两者都为矢量形式。
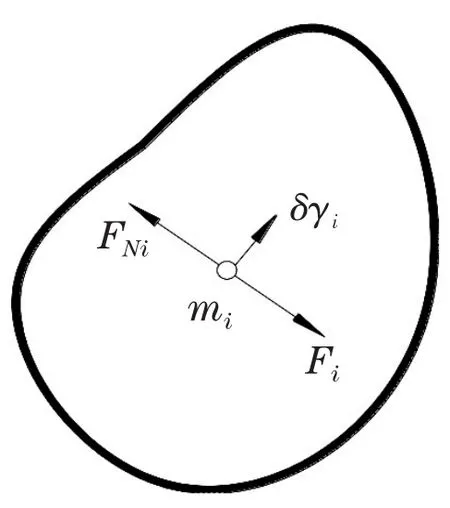
图1 质点受力与虚位移
1.2 虚位移原理的应用
1.2.1 虚设位移状态求未知力
如图2所示的计算简图,在求解此平衡体系中的未知力或者约束反力时,如果利用平衡方程进行求解,需要至少两个方程才能解出FA,求解过程见表1。
而利用虚位移原理进行求解时,把杆件看作刚体体系,虚设位移状态,求未知力。例如利用表1中的计算简图求解A点竖向约束反力,只需要将A点固定端支座变为滑动支座,同时把竖直约束力FA画在图上,然后在A点虚设单位位移AA'=1,画出此机动体系位移图,如表1图中虚线所示。应用虚位移原理,用一个方程即可求出FA。
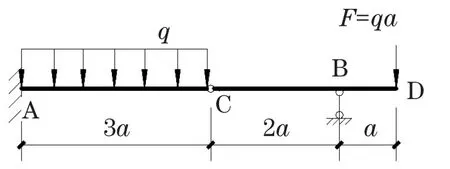
图2 计算简图示例
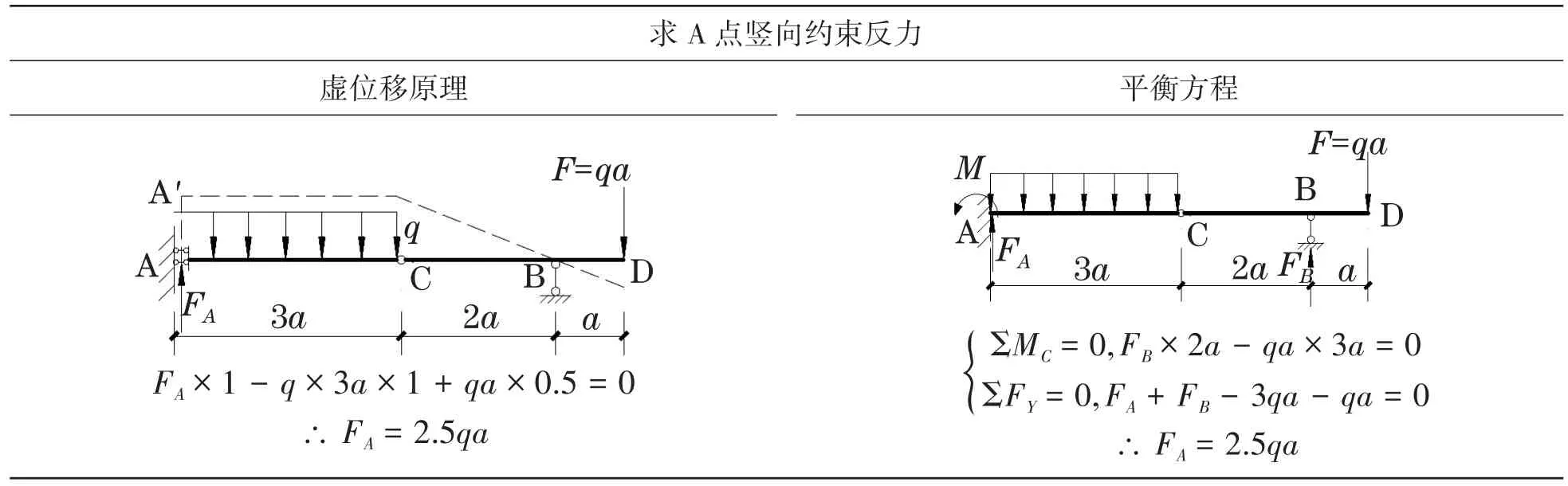
表1 虚设位移状态求未知力
1.2.2 虚设力状态求未知位移
在求解梁式杆件中某点位移时,我们还可以利用挠曲线近似微分方程EIw′′=-M(x)进行求解,也可以利用叠加法进行求解。利用挠曲线近似微分方程求解时,需要积分两次得到挠度方程,再利用边界条件和连续条件求出积分常数。如果杆件的内力方程有3个,积分常数就会有6个,联立6个方程进行求解,工作量较大,且很容易出错。
利用虚位移原理求解时,把梁式杆件看作变形体体系,虚设力状态,求未知位移。同样如图2所示的计算简图,要求解D点竖向位移。首先求出结构在外荷载作用下的轴力FNP,剪力FQP,弯矩MP,接着单独在D点作用一竖向单位荷载1,计算结构在单位荷载作用下的轴力N,剪力Q,弯矩M[3],对梁来说,轴力和剪力对其变形影响很小,可以忽略不计,只考虑弯矩的影响。因此利用下面公式中最后一项即可求得D点竖向位移,见表2,并且由此公式演化而来的图乘法,可以简化计算,不再赘述。
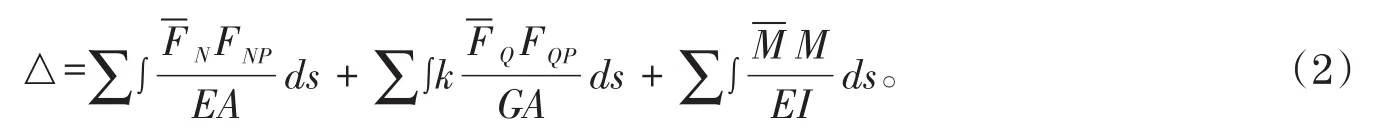
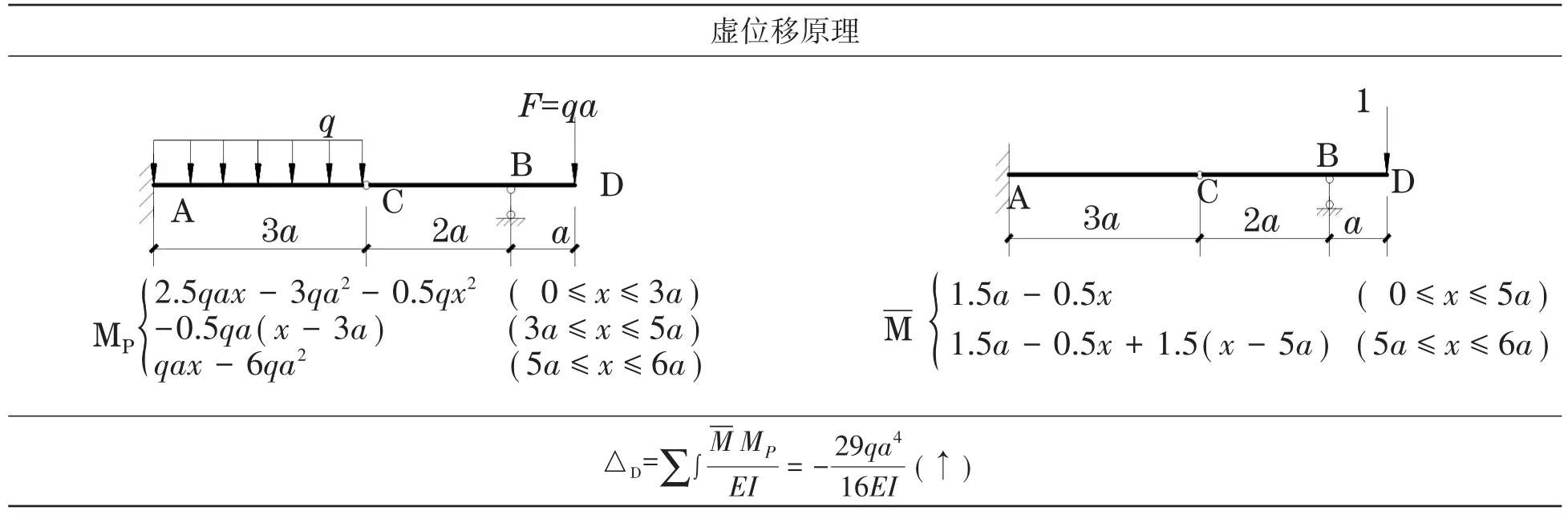
表2 虚设力状态求未知位移
2 虚位移原理求解内力方程
内力方程是画内力图的前提,传统教材中求解内力方程都是采用截面法,一般解题步骤为:求解支座约束反力,在某一截面处切割杆件后选取研究对象,在梁上截切梁段,在截面处代之以内力,画出已知的主动力和约束反力,在截面处画出轴力、剪力、弯矩等内力,并列出平衡方程求解内力方程。使用截面法,需要先求出支座反力,步骤较多,而且一旦支座反力求解错误,就会导致后续计算失效。使用虚位移原理进行求解内力方程,只需要把某梁段左右截面之间变成铰接点或者滑动支座,代上一对大小相等、方向相反的弯矩或者剪力,画出此时机动体系的位移图,根据几何关系求解各主动力相应的位移,列出虚位移方程,即可获得该段梁的内力方程。这种方法省去了求解支座约束反力这一步骤,直观易懂,不失为一种有效的方法。下面将以图2所示的计算简图为例,阐述利用虚位移原理求解内力方程的方法。
2.1 虚位移原理求弯矩方程
首先,将在AC段的F点连接变成铰接点,代上一对大小相等,方向相反的内力M,如图3(a)所示。然后做出机动体系的位移图,图中虚线表示相对位移,使∠CFE=1,如图3(b)所示。
则由虚位移原理可得:
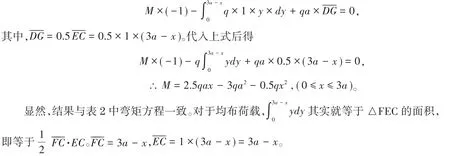
同理可以得到CB段和BD段的弯矩方程计算简图,如图3(c)、图3(d)所示。
经过位移分析,由虚位移原理得到:
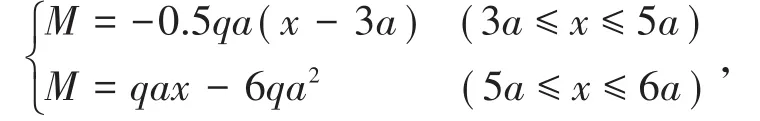
此结果与表2中弯矩方程也一致。
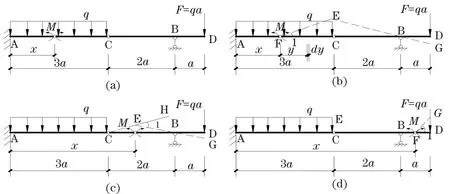
图3 梁式杆弯矩方程计算简图
2.2 虚位移原理求剪力方程
首先,将在AC段的F点连接变成滑动支座,代上内力FS,如图4(a)所示。然后做出机动体系的位移图,使,如图 4(b)所示。
则由虚位移原理可得:

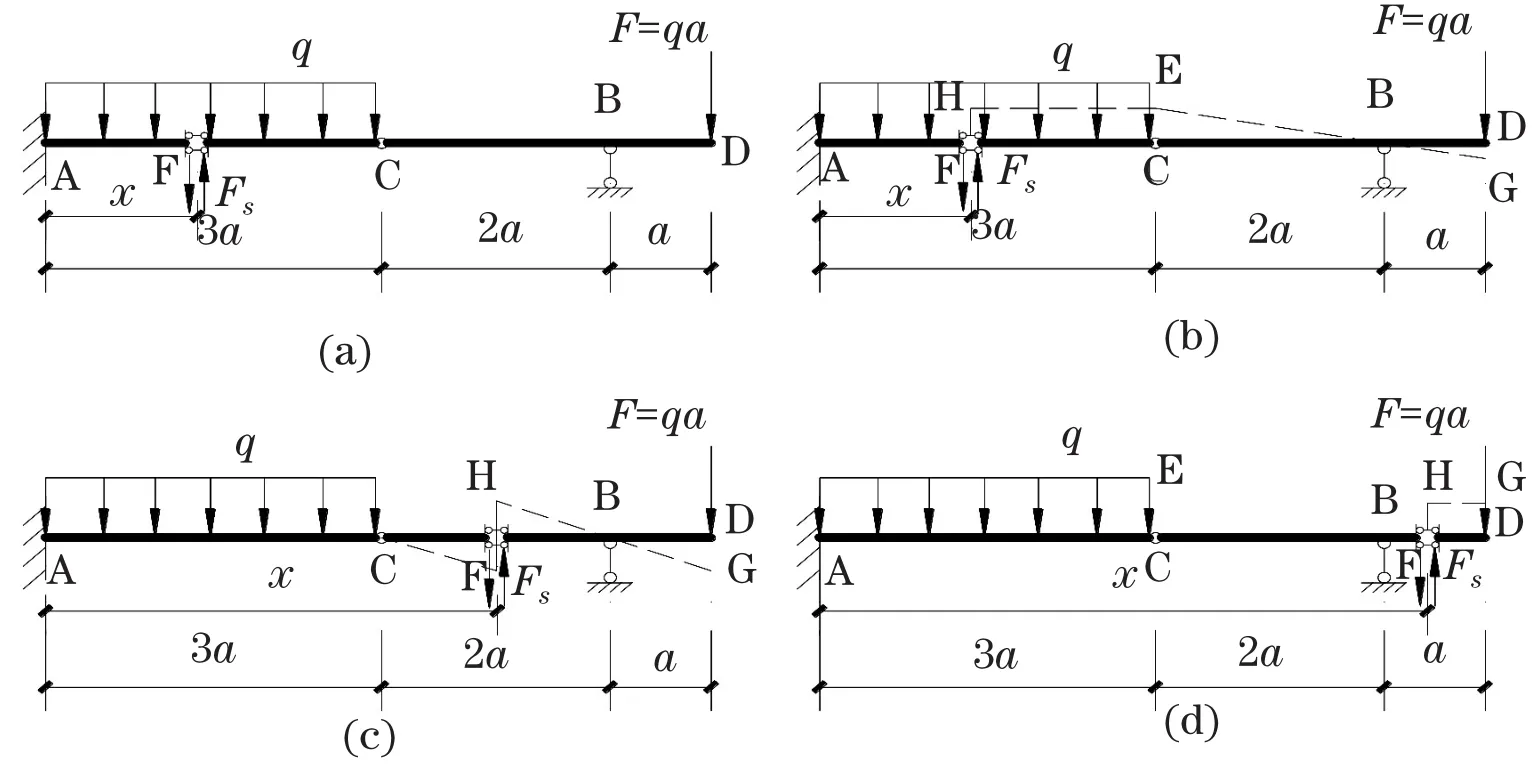
图4 梁式杆剪力方程计算简图
根据虚位移原理求得以下剪力方程:
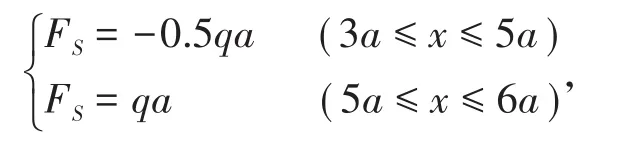
此结果与静力平衡计算结果一致。
3 结语
虚位移原理是基于功能的概念分析系统的平衡问题,在力学求解中应用广泛,是解析法与几何法的有机结合。利用虚位移原理求解弯矩方程和剪力方程,形象直观,思路清晰,计算结果准确可靠,是一种行而有效的方法。

