全变换图Gxyz∗

李亚平，吴宝音都仍

(新疆大学 数学与系统科学学院, 新疆 乌鲁木齐, 830046)

0 引言

设G=(V(G),E(G)) 是一个简单无向图. 对没有说明的术语和概念可参考[1, 2]. 图G的一个点v, 在G中的度记为dG(v),v的邻点记为NG(v) 是{u∈V(G)|uv∈E(G)}. 两个点u和v之间的距离dG(u,v)是它们之间最短路的长度.

我们用符号∆(G),δ(G),κ(G),λ(G),α(G),α′(G) 和ω(G) 分别表示G的最大度, 最小度, 连通性, 边连通性,独立数, 匹配数和团数. 图G的连通性(边连通性)记为κ(G)(λ(G)), 被定义为使G是k−连通的(k−边连通的)最大整数k. ∆′(G)=max{dG(u)+dG(v)|uv∈E(G)}.

图G的补图, 记为, 它的点集与G的相同, 且其两个点相邻当且仅当它们在G中不相邻. 图G的线图, 记为L(G), 它的顶点为E(G), 两个点相邻当且仅当在G中它们作为边是相邻的. 图G的全图T(G) 的点集是V(G)∪E(G), 且两个点相邻当且仅当它们在G中相邻或关联.

设G=(V(G),E(G)) 是一个图, 且α,β是V(G)∪E(G)的两个元素. 如果α和β在G中是相邻的或关联的,我们就说它们的关系是+. 设xyz是集合+,−的3-置换. 如果α和β都在V(G)中(分别地,α和β都在E(G) 中或α和β中的一个在V(G)另一个在E(G)中), 我们就说α和β对应于xyz的第一项x(分别地, 第二项y或第三项z).

图G的变换图Gxyz定义在点集V(G)∪E(G)上,Gxyz的两个点α和β是由一条边相邻的当且仅当它们在G中的关系和xyz的对应项相一致.因为有+,−的8个不同的3-置换,我们得到了8个图G的变换图. 有趣的是G+++恰好是G的全图T(G), 且G−−−是T(G)的补图. 又对给定的图G,G++−和G−−+,G+−+和G−+−,G−++和G+−−是其它的3对互补图.

变换图Gxyz作为全图的变换是由吴和孟[1]在2001年首次引进的，所有这些变换图都具有很多好的性质.

1 基本性质

若uv是G中的一条边, 则我们用euv记为Gxyz中的点. 吴和孟[1]给出了Gxyz是连通的充分必要条件, 对每个xyz, 他们证明了Gxyz有好的连通性质.

定理1(吴和孟[1]) 对给定的图G,G+++连通当且仅当G是连通的.

定理2(吴和孟[1]) 对给定的图G,G++−连通当且仅当G至少有两条边, 且G2K2.

定理3(吴和孟[1]) 对给定的图G,G+−+连通当且仅当G没有孤立点.

定理4(吴和孟[1]) 对一个图G,G+−−连通当且仅当G至少有两条边.

定理5(吴和孟[1]) 对任何图G,G−++是连通的.

定理6(吴和孟[1]) 对一个图G,G−+−连通当且仅当G不是星图.

定理7(吴和孟[1]) 对任何图G,G−−+是连通的.

定理8(吴和孟[1]) 对一个图G,G−−−连通当且仅当G既不是星图也不是三角形.

2 直径

有趣的是，对一个图G, 除了当xyz=+++ 时的情况, 如果Gxyz是连通的, 则它的直径不大（不超过4）.

定理9(吴和孟[1]) 若G连通, 则

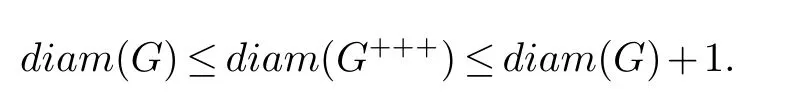
定理10(吴和孟[1]) 若G至少有两条边, 且G2K2, 则

等号成立当且仅当G2K2mK1,m>0.

定理11(吴和孟[1]) 若G没有孤立点, 则

等号成立当且仅当G同构于两个星图的不交并.

定理12(吴和孟[1]) 若G至少有两条边, 则

等号成立当且仅当GP3.

定理13(吴和孟[1]) 设G是一个图, 则

等号成立当且仅当diam(L(G))>2.

定理14(吴和孟[1]) 若G不是星图, 则diam(G−+−)≤3.

定理15(吴和孟[1]) 对任何图G,diam(G−−+)≤3, 等号成立当且仅当G包含一个三角形, 且图G有一个度为2的点.

定理16(吴和孟[1]) 若G既不是星图也不是三角形, 则diam(G−−−)≤3.

3 正则性

很明显G是正则的当且仅当是正则的. 林和束[3]对Gxyz是正则的给出了充分必要条件.

定理17(林和束[3]) 若G是简单图, 则G+++和G−−−是正则的当且仅当G是正则的.

定理18(林和束[3])设G是一个n≥3 阶的连通图,G++−和G−−+是正则的当且仅当GCn或K2,n−2或K4.

定理19(林和束[3]) 设G是一个n≥2 阶图, 且边数为m,G+−+和G−+−是正则的当且仅当G=C5或K2或K7或K3,3或C3□K2.

定理20(林和束[3])设G是一个n阶图,且边数为m≥1,G−++和G+−−是正则的当且仅当G是正则图.

4 平面性

在平面上画一个图时, 如果它的边只相交在端点, 则称这样的图为可嵌入平面的, 或可平面的. 图的这种画法叫做图的平面嵌入. 著名的Kuratowski’s 定理[4]说一个图是可平面的, 当且仅当它不含K5或K3,3的剖分图.

下面所有的定理都可从Kuratowski’s 定理推导出. 若两个图G和H满足V(G)∩V(H)=∅, 则它们的不交并记为G+H.

定理21(Behzad[5]) 图G的全图G+++是平面的当且仅当∆(G)≤3 且每个度为3的点是一个割点.

定理22(袁和刘[6]) 给定一个图G,G++−是平面的当且仅当|E(G)|≤2 或G∈{C3,C3+K1,P4,P4+K1,P3+K2,P3+K2+K1,K1,3,K1,3+K1,3K2+K1,3K2+2K1,C4,C4+K1}.

定理23(王和刘[7]) 设G是边数为m的图, 则G+−−是平面的当且仅当m≤2 或G同构于下列图中的一个:C3,C3+K1,P4,P4+K1,P3+K2,P3+K2+K1,K1,3,K1,3+K1,3K2,3K2+K1,3K2+2K1,C4,C4+K1,2P3.

定理24(吴, 张, 张[8]) 给定一个图G,G−++是平面的当且仅当|V(G)|≤4.

定理25(王[9]) 给定一个图G,G−+−是平面的当且仅当n≤4 且G不同构于K4−e.

定理26(王[9]) 给定一个图G,G−−+是平面的当且仅当n≤3 或G同构于下列图中的一个: 2K1+K2,K1+K1,2,K1,3,K1+C3.

定理27(刘[10]) 设G是阶数为n的图, 则G−−−是平面的当且仅当n≤3 或G同构于下列图中的一个:2K2,C4,K4−e,K4,2K+K3,K1,4,K1+K1,3,2K1+P3.

现在只有当xyz=+−+ 的情况还没有解决.

5 同构

Gr¨unbaum[11]对任何图的变换构造了如下两类基本问题: (1)确定性问题. 确定哪些图有一个给定的图作为它们的Gxyz；(2)刻画性问题. 刻画那些图, 它是某个图的变换图Gxyz.

定理28(吴和孟[1]) 给定一个图G,

(i)G+yz=G当且仅当G是一个空图;

(ii)G−yz=G当且仅当G=K1.

定理29(吴, 张, 张[8]) 给定两个图G和G′,G−++=G′−++当且仅当G=G′.

定理30(吴, 张, 张[8]) 给定两个图G和G′,G+−−=G′+−−当且仅当G=G′.

猜想1(吴, 张, 张[8]) 给定两个图G和G′,G++−=G′++−当且仅当G=G′.

猜想2(吴, 张, 张[8]) 给定两个图G和G′,G+−+=G′+−+当且仅当G=G′.

有关Gxyz刻画问题未被解决.

6 哈密顿性, 连通性和独立数

6.1 哈密顿性

设G是一个图. 如果一个圈包含图G的所有顶点, 则这个圈称为G的哈密顿圈. 一个图若包含哈密顿圈, 则称这个图是哈密顿图. 由Chv´atal 和Erd˝os[12]的定理, 我们知道阶至少是3的图G, 如果满足κ(G)≥α(G), 则G是哈密顿的.

EPS-子图是由Fleischner 在文献[13]中首次引入的, 图G的EPS-子图是一个连通的支撑子图S,S是图E和森林P的边不交并,E(不一定连通)的所有顶点的度数都是偶度, 森林P(可能为空)的每一个分支是一条路.

定理31(Fleischner和Hobbs[14]) 设G是至少有两个点的有限图, 则G的全图G+++是哈密顿的当且仅当G包含一个EPS-子图.

以下关于Gxyz的哈密顿性的大部分定理都是从上面Chv´atal-Erd˝os定理推导出来的.

定理32(马和吴[15]) 设G是一个图. 则G−−−是哈密顿的当且仅当G不同构于以下的任何图{K1,r|r≥1}∪{K1,s+K1|s≥1}∪{K1,t+e|t≥2}∪{K2+2K1,K3+K1,K3+2K1,K4}.

定理33(吴, 张, 张[8]) 若G是阶数为n的图,G−++是哈密顿的当且仅当n≥3.

定理34(徐和吴[16])若G是阶数为n≥4的图,G−+−是哈密顿的当且仅当G不同构于以下的任何图{K1,n−1,K1,n−1+e,K1,n−2+K1}{2K1+K2,K1+K3}.

定理 35(甄和吴[17]) 若G是没有孤立点的图,G+−−是哈密顿的当且仅当G既不是星图, 也不是G∈{2K2,K3,K1,1}.

定理36(伊和吴[18]) 设G是阶为n≥6的图, 且边数为m. 若m≥α(G)+1, 则G++−是哈密顿的.

推论1(伊和吴[18]) 设G是阶为n≥6的图, 且边数为m. 若m≥n, 则G++−是哈密顿的.

6.2 连通性

定理37(Sim˜oes-pereira[19])

上述下界可进一步改进.

定理38(Hamada和Nonaka和Yoshimura[20])

定理39(Bauer 和Tindell[21]) 若λ(G)≥2, 则λ(G+++)=δ(G+++)=2δ(G).

定理40(张和黄[22]) 给定一个图G,κ(G+−+)=δ(G+−+) 当且仅当下面三个条件都不满足:

(1)G至少有两个分支, 其中一个是K2, 且δ(G)≥1;

(2)G至少有两个分支, 其中一个是K3, 且δ(G)≥2;

(3)G=K1,n.

推论2(张和黄[22]) 若G2K2, 则λ(G+−+)=δ(G+−+).

定理41(徐和吴[16])设G是阶为n的图,且边数为m,则或min{δ(G−+−),n+κ(L(G)),m+κ(G)}.

定理42(伊和吴[18]) 设G是阶为n≥6的图, 且边数为m≥3, 则κ(G++−)≥min{m−1,n+κ(L(G))−1}.

推论3(徐和吴[16]) 设G是阶为n≥4的图, 则以下情形等价:

(1)κ(G−+−)≥2;

(2)δ(G−+−)≥2;

(3)G/∈{K1,n−1,K1,n−1+e,K1,n−2+K1}.

推论4(徐和吴[16]) 设G是阶为n≥4的图,κ(G−+−)=2 当且仅当δ(G−+−)=2.

定理43(甄和吴[17]) 设G是阶为p的图, 且边数为q,

6.3 独立数

引理1(马和吴[15]) 对一个给定的图G, 如果∆(G)=1则α(G−−−)=3, 否则α(G−−−)=∆(G)+1.

定理44(马和吴[15]) 对任何图G,

等号成立当且仅当G包含一个三角形, 且∆(G)=2.

定理45(徐和吴[16]) 对任何图G,

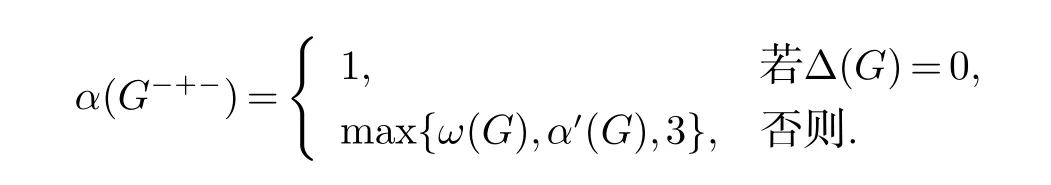
定理46(吴, 张, 张[8]) 对任何图G,λ(G−++)=δ(G−++).

定理47(甄和吴[17]) 对任何图G,

定理48(伊和吴[18]) 对任何图G,

7 超边连通性和圈边连通性

7.1 超边连通性

若图G满足λ(G)=δ(G), 则称它为极大边连通的, 或简称G是max-λ. 如果对图G的每个最小边割T,G−T有孤立点, 则称它为超边连通的, 或简称G是super-λ.

定理49(陈和孟[23]) 若G是连通图, 则G+++是super-λ当且仅当下面两个条件之一成立:

(1)λ(G)≥2, 若G有一个割点x, 且dG(x)=δ(G), 则在x和G−x的任何分支之间存在3条或更多边;

(2)λ(G)=1, 若e=xy是一个桥, 则min{dG(x),dG(y)}≥2δ(G).

定理50(陈和孟[23]) 设G是没有孤立点的连通图,G+−+是super-λ当且仅当G没有孤立边且GK1,n.

定理51(陈和孟[23]) 给定图G,G−++是super-λ当且仅当GK1,n或K1,n∪K1.

推论5(陈和孟[23]) 对任何图G,λ(G−++)=δ(G−++).

定理52(陈和孟[24]) 对任何图G,G−−+是max-λ并且G−−+是super-λ当且仅当G既不同构于K1,2也不同构于K2∪K1.

推论6(陈和孟[24]) 对任何图G,λ(G−−+)=δ(G−−+).

定理53(陈和孟[25]) 若G是至少有两条边的图,G++−是super-λ当且仅当下面条件成立:

(1)G2K2∪mK1,K1,2∪mK1,K3∪mK1, 2K3,m是非负整数;

(2)GK2∪K3,K2∪P3,P4,Pi是一条长为i−1 的路.

推论7(陈和孟[25]) 若G至少有两条边, 且G2K2, 2K2∪K1,K2∪P3, 则λ(G++−)=W(G++−).

定理54(陈和孟[26]) 给定图G，G+−−是max-λ当且仅当G至少有两条边, 且G2K2.

定理55(陈和周和黄[27]) 所有的连通变换图G−+−是max-λ.

定理56(陈和孟[23]) 给定图G, 若G−−−是连通的, 则λ(G−−−)=δ(G−−−).

7.2 圈边连通性

设G是连通图.G的一个边割是它的边子集F⊆E(G)使G−F中至少有两个连通分支. 图G的圈边割是它的一个边割F使得G−F至少有两个连通分支包含圈. 圈边连通度cλ(G) 是最小圈边割的基数. 所有的圈可分图G满足cλ(G)≤ϖ(G)[28], 这里ϖ(G)=min{ϖ(X)=[X,] :X能导出G的最短圈}.

定理57(陈,朱,江[29])对于一个图G,G++−是连通的且是圈可分的当且仅当G至少包含两条边,G/=2K2且G/=K1,2∪mK1,m≥0.

推论8(陈, 朱, 江[29]) 对于一个图G,G++−是连通的且是圈可分的当且仅当G至少包含三条边, 或G=2K2∪mK1,m≥1.

定理58(陈, 朱, 江[29]) 对于一个图G, 若G++−是连通的且是圈可分的, 则

定理59(陈, 朱, 江[29]) 设图G是连通的, 且G++−是连通的且是圈可分的, 则

8 拓扑指标

一个分子图是把分子的原子看作图的点, 把分子的键看作图的边得到的. 分子图的图理论的不变量被认为是拓扑指标, 用来预测相应分子的性质.

8.1 Zagreb 指标

第一和第二Zagreb指标是最早的著名拓扑指标之一,是Gutman等人在文献[30]中引入的,他们用来测量全π-电子能对化学结构的依赖性. 第一Zagreb和第二Zagreb指标分别定义为：

和

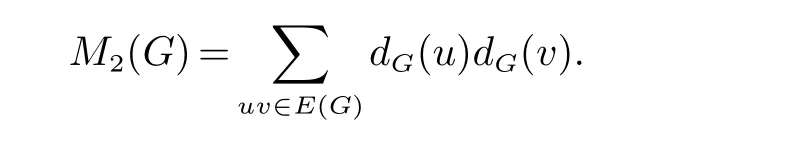
图G的补图的所有边的和,这样的不变量叫做Zagreb补指标.更确切地,图G的第一第二Zagreb补指标在[31]中分别定义为:

和

在[32]中, De 定义了

在[33]中, 对正整数k∈{1,2,3}, 定义了则ξ1(G) 是G边数的两倍,ξ2(G) 是第一Zagreb 指标.

定理60(Hosamani 和Gutman[33]) 若G是阶为n的图, 且边数为m, 则

推论9(Hosamani 和Gutman[33]) 若G是阶为n的图, 且边数为m, 则

8.2 F-指标

一个拓扑指标在[30]中被证明能影响全π-电子能, 这个指标被定义为图顶点的度的立方的和. Furtula 等人在[34]中研究了这个指标并且给出了一些基本性质. 他们把这个指标命名为“遗忘拓扑指标”或F-指标, 记为F(G), 因此

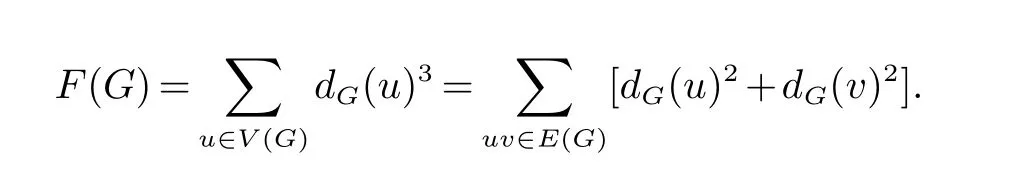
Ranjini等人在[35]中引入了新的Zagreb指标:

定理61(De[32]) 若G是阶为n的图, 且边数为m, 则

定理62(De[32]) 若G是阶为n的图, 且边数为m, 则

定理63(De[32]) 若G是阶为n的图, 且边数为m, 则

定理64(De[32]) 若G是阶为n的图, 且边数为m, 则

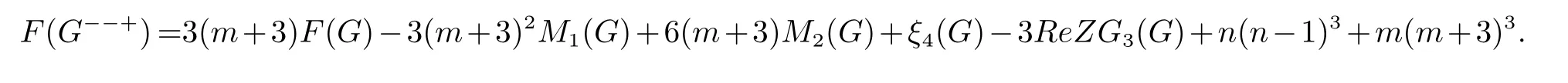
定理65(De[32]) 若G是阶为n的图, 且边数为m, 则

定理66(De[32]) 若G是阶为n的图, 且边数为m, 则

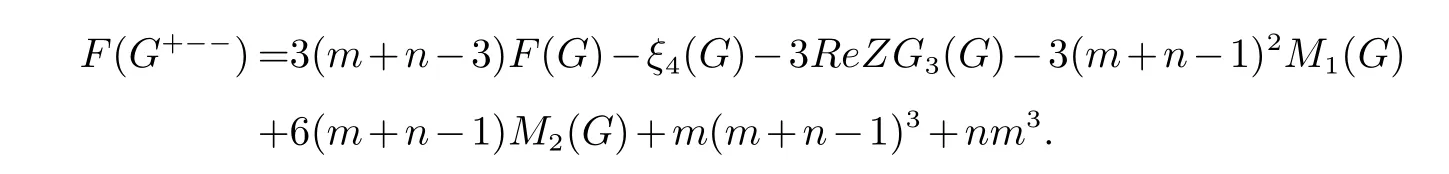
定理67(De[32]) 若G是阶为n的图, 且边数为m, 则

定理68(De[32]) 若G是阶为n的图, 且边数为m, 则

8.3 NK-指标

在1984, Narumi 和Katayama 在[36]中引入了图的一个乘法的不变量，用于表示饱和烃的碳骨架，并命名为“简单拓扑指标”. Tomovic 和Gutman 在[37]中把这个指标重新命名为“Narumi-Katayama 指标”或“NK-指标”并且记为NK(G). 图的Narumi-katayama指标定义为所有顶点度的乘积, 即

Eliasi, Iranmanesh和Gutman在[38]中引入了一个新乘法的图的不变量称为乘积形式的Zagreb 指标，其定义为:

定理69(De[39]) 若G是阶为n的图, 且边数为m, 则

定理70(De[39]) 若G是阶为n的图, 且边数为m, 则等号成立当且仅当G是正则图.

定理71(De[39]) 若G是阶为n的图, 且边数为m, 则

等号成立当且仅当G是正则图.

定理72(De[39]) 若G是阶为n的图, 且边数为m, 则

等号成立当且仅当G是正则图.

定理73(De[39]) 若G是阶为n的图, 且边数为m, 则

定理74(De[39]) 若G是阶为n的图, 且边数为m, 则

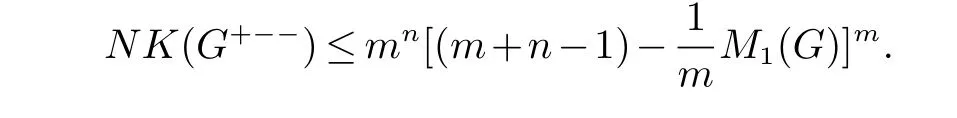
等号成立当且仅当G是正则图.

定理75(De[39]) 若G是阶为n的图, 且边数为m, 则

等号成立当且仅当G是正则图.

定理76(De[39]) 若G是阶为n的图, 且边数为m, 则

等号成立当且仅当G是正则图.

9 谱

图G的邻接矩阵是n×n矩阵A(G):=(auv), 其中auv是连接顶点u和v的边数. 矩阵A(G)的特征多项式叫做图G的特征多项式, 记为PG(λ).

定理77(Cvetkovi´c 和Doob 和Sachs[40])设G是一个有n个点,m条边的r−正则图(r>1). 如果G的特征值是λ1≥λ2≥···≥λn, 则G+++有m−n个特征值是-2, 其余的2n个特征值是:

由定理77证明可得:

定理78(颜和许[41]) 设G是一个有n个点,m条边的r−正则图. 如果G的特征值是λ1≥λ2≥···≥λn, 则

10 谱半径

设G是一个阶为n的简单图, 设A(G)为图G的邻接矩阵. 图G的谱半径ρ(G)定义为邻接矩阵A(G) 的最大的特征值.

定理79(林和束[3]) 设G是一个有n≥3 个点,m条边的连通图. 则

定理80(林和束[3]) 设G是一个有n≥2 个点,m≥2 条边的连通图, 且G/=2K2. 则

定理81(林和束[3]) 设G是一个有n≥3 个点,m条边的连通图. 则

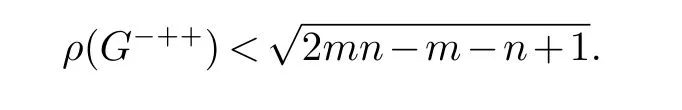
定理82(林和束[3]) 设G是一个有n≥2 个点,m条边的连通图, 且G不是星图. 则

定理83(林和束[3]) 设G是一个有n≥3 个点,m条边的连通图并且没有孤立点. 则

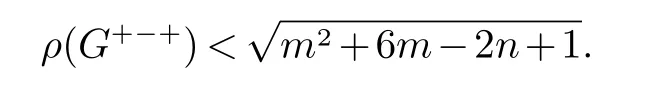
定理84(林和束[3]) 设G是一个有n≥2 个点,m条边的连通图并且没有孤立点. 则

定理85(林和束[3]) 设G是一个有n≥3 个点,m条边的连通图并且没有孤立点. 则

定理86(林和束[3]) 设G是一个有n≥3 个点,m条边的连通图并且没有孤立点, 又G既不是K3也不是星图. 则

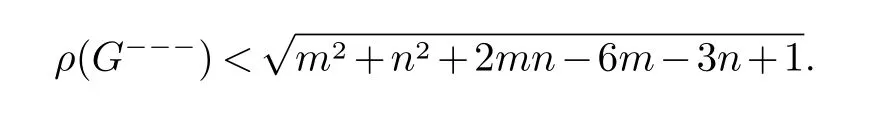
11 Laplacian 谱

设D(G) := (dij) 是n×n的矩阵,dii=dG(vi) 且dij= 0,i/=j. 矩阵D(G) 和L(G) =D(G)−A(G) 分别是图G的度矩阵和Laplacian矩阵. 图G的Laplacian 多项式, Laplacian 谱和Laplacian 特征值分别是特征多项式L(λ,G)=det(λI−L(G)),L(G)的谱和其特征值.

定理87(邓和Kelmans 和孟[42]) 设G是一个有n个点,m条边的r−正则图. 则

定理88(邓和Kelmans 和孟[42]) 设G是一个有n个点,m条边的r−正则图, 并且设s=n+m. 则

12 控制

在图G中如果一个点和边是关联的, 则称这样的点和边是相互覆盖的. 点覆盖是覆盖图G中所有边的点集,边覆盖是覆盖图G中所有点的边集. 图G的点覆盖的最小基数叫做G的点覆盖数, 记为β(G). 图G的边覆盖的最小基数叫做G的边覆盖数, 记为β1(G).

如果V−S中的每个点在S中至少有一个邻点, 则S⊆V(G)是一个控制集. 图G的所有控制集的最小基数叫做G的控制数, 记为γ(G). 边控制的概念是由Mitchell 和Hedetniemi在[43]中提出的, 如果不在X中的每条边在X中有一些相邻的边, 则边集E(G)的子集X叫做图G的边控制集. 图G的边控制数γ′(G)是G的所有边控制集的最小基数[43].

Sampathkumar 和Latha在[44]中引入了强控制和弱控制的概念. 若uv∈E(G), 则u和v相互控制. 进一步, 如果dG(u) ≥dG(v), 则u强控制v且v弱控制u. 如果V(G)−D中的每个点v被D中的一些点强控制, 则集合D⊆V(G)是G的强控制集(sd−set).G的强控制数γs(G)是强控制集的最小基数. 类似地, 如果V(G)−W中的每个点被W⊆V(G)中的点弱控制，则W被称作G的弱控制集(wd−set).G的弱控制数γw(G) 是wd−set的最小基数.

Ayta¸c和Turaci对Gxy+的控制数给出了一些界[45]. Jebitha 和Joseph 对G+−+的控制数给出了一些上界[46],Jebitha 和Joseph 引进了一个新参数叫做图G的独立边控制数(记为从而对任何图G确定了G−+−的控制数[47].

定理89(Ayta¸c 和Turaci[45])设H是有n个点的连通图并且仅包含一个悬挂点. 若对dH(u)=1 和v∈NH(u),图G=H−euv有n个点, 且是r−正则的, 则

定理90(Jebitha 和Joseph[46]) 对任何图G,γ(G)≤γ(G+−+)≤γ(G)+2 且界是紧的.

定理91(Jebitha 和Joseph[46]) 设G是阶为n≥5的连通图. 则且界是紧的.

定理92(Jebitha 和Joseph[46]) 若G是一个连通图, 且∆(G)=n−2, 则γ(G+−+)≤3.

定理93(Jebitha 和Joseph[46]) 如果一个图G的diam(G)=2, 则γ(G+−+)≤δ(G)+1 且界是紧的.

定理94(Jebitha 和Joseph[46]) 对任何连通图G, ∆(G)

定理95(Jebitha 和Joseph[46]) 设G是阶为n >2的连通图, ∆(G) =n−1 且v是一个度为∆(G)的顶点.则γ(G+−+)=2 当且仅当〈N(v)〉 是非空的并且包含K1或K2或同构于K1,r,r≥2.

定理96(Ayta¸c 和Turaci[45]) 设G是一个有n个点,m条边的连通图, 则γ(G−++)≤1+γ′(G).

定理97(Ayta¸c 和Turaci[45]) 设G是一个有n个点连通图, 并且是r−正则的. 若n>2r+1, 则

定理98(Ayta¸c 和Turaci[45]) 设G是一个有n个点连通图, 并且是r−正则的. 若n<2r+1, 则

定理99 (Ayta¸c 和Turaci[45]) 设G是一个有n个点,m条边的连通图, 则γ(G+−+)≤β(G).

定理100(Ayta¸c 和Turaci[45])设G是一个有n个点,m条边的连通图,若G仅包含一个悬挂点且点的最大度为∆(G)=n−1, 则γ(G+−+)=2.

定理101(Ayta¸c 和Turaci[45]) 设G是一个有n个点的连通图, 并且是r−正则的. 若r >3, 则γ(G−−+)=γw(G−−+)≤β(G) 和γs(G−−+)≤n−β1(G).

定理102(Jebitha 和Joseph[47]) 对任何图G,γ(G−+−)≤3. 进一步,

(i)γ(G−+−)=1 当且仅当δ(G)=0;

(ii)γ(G−+−)=2 当且仅当diam(G)≥3 或G有一个边数为2的匹配.