基于“以线带面”的交通信号网络协调控制方法

（北方工业大学城市道路交通智能控制技术北京市重点实验室，北京 100043）

城市交通拥堵日益严重，交通控制成为解决交通拥堵的快速有效的途径之一，城市路网中交叉口之间息息相关，各个交叉口之间的交通状况相互影响。人们采用“绿波带”的形式对道路交通进行协调，取得了良好的效果。何永明[1]提出了采用模糊控制的方法设计城市交通绿波协调控制，将多路口的绿波带划分为若干个协调控制相位差优化的双路口子系统。通过子系统的逐级串联，完成整个绿波干线上的相位差计算。该方法避免建立绿波带内各路口的综合模型，减少了模糊规则和计算量，避免了多路口综合协调控制下的模糊规则爆炸问题，同时减少了多个路口控制机之间的数据交换。曲大义、万孟飞[2]等提出了基于交通波理论的干线绿波协调控制方法，考虑到了城市干线各交叉口间的关联性，运用交通波理论阐释了干线车流排队现象，揭示了大流量线控系统绿波交通产生的内在机理。从周期、相位相序、绿信比、相位差等4种控制参数入手，对干线绿波交通进行了优化研究。吴中、张静伟[3]提出基于路中变速的城市双向绿波研究，通过在路段中设置最佳变速点，消除变速产生的交通波对交叉口的影响，并使绿波车流能够以恒定的速度通过交叉口，提高了交叉口的安全性和通过能力。利用变速提示牌指示驾驶员变速的方法成本低可操作性强实施方便。但是“绿波带”的协调是以牺牲支路的通行能力为基础的，只能实现干线通行能力的提高，对整个路网的提升效果不高。为此，2016年，潘科[4]在综合绿波控制的基础上进一步拓展，提出子干线的概念，建立了基于子干线模型的干线双向绿波带优化模型。并以此为基础，将子干线模型绿波带控制方法应用到路网中，设计了一种基于子干线模型的南北、东西向均有绿波效果的网络绿波带。王昊、姚东成[5]提出了约束可松弛的网络绿波模型，可以通过松弛网络外圈闭环约束条件，获得网络绿波控制模型的最优解。但大多数学者的研究都未能解决区域绿波外圈约束问题。为此，本文采用“以线带面”的控制策略，将区域路网划分为若干条相交的干线，将干线绿波协调控制的方法拓展到区域路网中同时避开外圈闭环，以减少整体路网平均延误为目标，对路网进行协调控制优化，以缓解日益严重的交通拥堵问题。

1 研究对象

本文的研究对象为三条横向干线和三条纵向干线组成的理想交通路网，共形成9个交叉口，如图1所示。该路网也可拓展为实际复杂路网，具有普遍适用性。相位转换如图2所示。

图1 理想交通路网图

图2 相位转换图

图中每个交叉口相位为4相位分别为东西直行、东西左转、南北直行、南北左转。

2 控制策略

“以线带面”控制策略是采用分解协调的控制思想，将复杂的网络交通控制系统分解为多个干线交通控制，将干线交通控制的方法应用到网络交通，降低了控制的难度。

“以线带面”协调控制总体过程：

（1）根据交通流量和道路饱和度确定关键交叉口，此步骤依靠交通管理经验人为指定。

（2）根据道路交通流量和饱和度，将道路分级。

（3）按照道路等级依次设计协调路径。

一般来说关键交叉口的协调等级为最高，注意在设计过程中不能出现“闭环”。

（4）合理优化协调路径的相位相序。

控制策略流程如图3所示。

图3 控制策略流程图

以图1交通路网为例：

（1）人为指定4号路口为关键交叉口。

（2）假设道路划分等级。

第一等级：路段1→4→7和路段4→5→6；

第二等级：路段2→5→8；

第三等级：路段1→2→3、路段7→8→9、路段3→6→9。

（3）根据道路等级协调控制路径。在协调过程中，对每一次协调都要检查协调路径是否形成闭环，以防止出现“锁死”现象。首先对第一等级道路进行协调，把路段1→4→7和路段4→5→6设定为双协调路径进行协调。然后对第二等级道路进行协调，把路段2→5→8设定为双协调路径。最后对第三等级道路进行协调，为防止出现闭环，采用分段协调的方法，把路段2→3和路段8→9设定为单协调路径进行协调。最终协调结果如图4所示。1号、3号、6号、7号、9号为单协调交叉口，2号、4号、5号、8号为双协调交叉口。以上关键交叉口、单协调交叉口、双协调交叉口均为人为设定。

图4 协调后理想交通路网图

3 相位相序优化

目前我国常用的相序方案多数都是基于单环结构，至少会有两个方向的车流公用一个相位，但是由于城市道路交通流时空分布的不均衡性，公用相位中某一方向的车流必定不能有效使用该相位的全部绿灯时间。降低了该相位的绿灯时间使用效率[6]。故本文为提高绿灯时间的使用效率，采用NEMA双环、双段结构相位。

以上图路网单环相位转换图为例，转换为双环结构示意如图5所示。

图5 双环结构示意图

NEMA相位中，任意调整位于同环、同段的两个相位的时长和顺序，完全不会对交叉口中其他相位的正常运行产生任何不良影响。故相对于传统单环结构的配时方案，NEMA相位在处理相序和相位时长方面有着更高的灵活性[6]。双环结构绿波如图6所示。

图6 双环结构绿波示意图

gi(i=1,2,3,4)为每个相位的绿灯时长，Δt为相位重叠时长，Δg为隔断时间。可以根据交通流量的大小自由变换g1、g2或g3、g4的长度和，以节省交叉口车辆通行时间，提高通行效率。

4 相位差计算

相位差是指相邻路口同一相位绿灯（或红灯）起始时间之差，是由两个相邻路口之间的路段长度L和路段上行驶的实际车速v来决定的，相位差分为上行相位差ti,i+1和下行相位差ti+1,i，有：

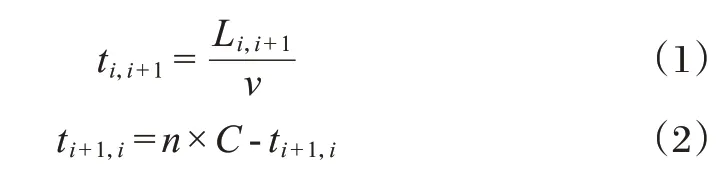
式中：i——控制子区内的某个交叉口；i+1——与i路口相邻的另一个路口；Li,i+1——从路口i到路口i+1之间的距离（m）；v——路段上实际车速（m/s）；n——整数；C——共同周期长（s）。

5 绿灯启动时间协调［7］

（1）将含有关键路口的第一等级道路进行协调。以关键路口的绿灯启动时间作为该协调路径上相位启动的基准时间，依次确定协调路径上其他路口的绿灯启动时刻。

（2）协调与（1）形成的协调路径相交的交叉口。且除（1）的道路外等级最高。并将该交叉口对应的相位启动时刻作为协调该路径上其他交叉口相位启动时间的基准时刻，同时将其生成的协调道路看作一个整体。

（3）协调与（2）生成的协调道路相交且协调等级最高的道路，并以该相交路口对应的相位启动时刻作为基准时刻，依次确定协调带上其他路口的启动时刻，同时将其生成的协调道路看作一个整体。

（4）以此类推，直到协调完毕。

以图1研究路网为例：

（1）4号交叉口为关键交叉口，包含4号交叉口的协调路径有2个，分别为路径1→4→7和路径4→5→6，选取路径1→4→7为主协调路径，以4号交叉口相位启动时刻作为基准时刻，分别确定1号交叉口和7号交叉口的相位启动时刻。

（2）与协调路径1→4→7形成4号关键交叉口的最高等级协调路径为4→5→6，故以4号交叉口相位启动时刻作为基准时刻对路径4→5→6中5号、6号交叉口进行协调。

（3）与协调路径4→5→6相交的最高等级协调路径为2→5→8，交叉口为5号交叉口，故以5号交叉口的相位启动时刻作为基准时刻对路径2→5→8中2号、8号交叉口进行协调。

（4）与路径2→5→8相交的路径包括2→3和8→9，以2号交叉口和8号交叉口的相位启动时刻为基准时刻，对3号交叉口和9号交叉口进行协调。至此，整个路网协调完毕。

6 验证与仿真

本文采用vissim对试验进行仿真验证，仿真路网如图7所示。

图7 仿真路网

各交叉路口进口道流量均为800 pcu/h。各交叉口之间的距离相等，均为386 m。设计车速为50 km/h。采用交互式协调控制方式，公用周期为60 s。仿真结果如表1所示。

表1 不同策略方案车辆平均延误表 单位：s

7 结语

本文采用“以线带面”的控制策略，将干线绿波协调控制方法应用到交通路网上，以形成网络绿波带的控制策略。通过这种控制策略的协调控制方法与普通固定信号配时策略进行对比，对比结果显示，采用“以线带面”控制策略的平均延误比普通固定配时策略的平均延误低29%。由此可见，“以线带面”的控制策略比普通固定配时更具有优越性。