低渗透油藏转向压裂产能预测及影响因素

蒲晓，郭大立，兰天，贺勇，赵运祥

（1.西南石油大学 理学院，成都 610500；2.中国石油 新疆油田分公司a.采油一厂；b.百口泉采油厂，新疆 克拉玛依 834000）

随着油气勘探开发难度不断增大，低渗和特低渗油藏逐渐受到关注[1-2]。低渗透油藏自然产量低，采油速度和采收率也都普遍偏低。水力压裂作为油气井增产的主要措施，为低渗透油气田的稳产做出了重要贡献[3-4]。但经过常规压裂改造后，很多区块会很快进入高含水阶段，达不到稳产增油的目的[5-6]。为了提高这类区块的产量，在克拉玛依油田进行了暂堵转向压裂技术的研究和应用。

暂堵转向压裂是在裂缝内实时添加暂堵剂，迫使裂缝转向的压裂技术[7-11]。转向压裂后，主裂缝周围存在多分支转向裂缝，多分支转向裂缝近似替代裂缝网络，增加了泄油面积，达到增产目的。产能模拟与产能影响因素分析是转向压裂优化设计的重要环节[12]，转向压裂后形成的转向裂缝系统分布无规律，增加了油藏产能的预测难度。前人对复杂裂缝网络产能预测的研究较多，但大多对复杂裂缝网络进行简化处理，并没有对裂缝网络进行精细表征，而且针对转向压裂进行产能预测的研究更少[13-18]。

本文利用局部网格加密技术，对转向裂缝系统进行表征，建立产能预测模型，并研究渗透率、裂缝导流能力和转向裂缝长度对产油量的影响。

1 产能预测模型

经过转向压裂形成的分支裂缝并不是简单的双翼对称裂缝，会在初级压裂裂缝周围产生多分支转向裂缝。因此，预测转向压裂的产能时，需要对转向裂缝系统进行分析，主要包括整体裂缝系统的分布特征，以及主裂缝和转向裂缝在坐标系中的位置、方位及大小。为了简化说明，假设转向裂缝系统中包含了9 条裂缝，对每条裂缝进行编号，裂缝1 为主裂缝，裂缝2—裂缝9为转向裂缝（图1）。在坐标系中，主裂缝平行于x轴，一级网格长度为20 m，可以确定每条裂缝的起始位置、长度、倾角以及平均曲率。确定裂缝的方位以及大小后，只对井附近和存在裂缝的地方进行局部加密，对转向裂缝进行三级网格剖分。本文采取在裂缝区域及井底附近对网格进行加密，其他区域为粗网格，减少了网格数量，提高了计算效率。

图1 转向裂缝精细描述及局部加密Fig.1.Detailed description and local refinement of steering fractures

对储集层中转向裂缝分析处理后，需要建立储集层中流动的渗流数学模型。模型假设条件：①考虑二维平面内的流体流动；②储集层中流体为微单相和微可压缩；③忽略储集层岩石的压缩性；④考虑储集层的非均质性和各向异性，储集层中的渗透率随位置的变化可改变；⑤不考虑重力的影响。则储集层中单相流动的数学模型为

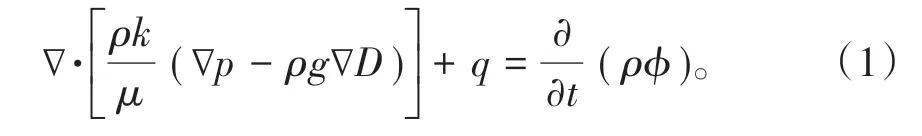
将（1）式简化为二维平面内的非均质油藏，若忽略重力的作用，在考虑网络裂缝系统的条件下，可表示为

假设条件岩石不可压缩和流体微可压缩，（2）式可表示为

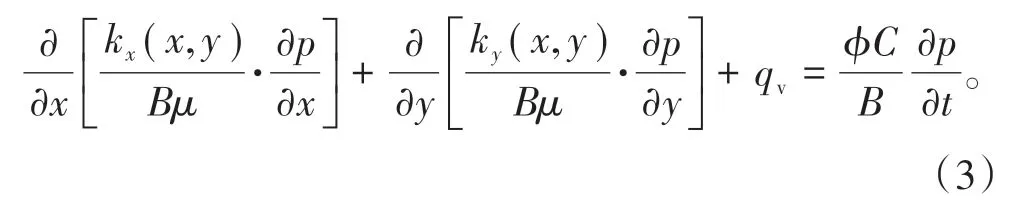
其中，初始条件为p（x,y,0）=pi，（0≤x≤Lx，0≤y≤Ly）。根据建立的模型和网格系统特点，采用隐式差分格式的有限差分法，对数学模型进行差分，得到差分方程：

令Qvi，j为网格（i，j）的源汇项，vi，j为网格（i，j）的孔隙体积，Txi±1/2为x方向的传导系数，则（4）式可以表示为

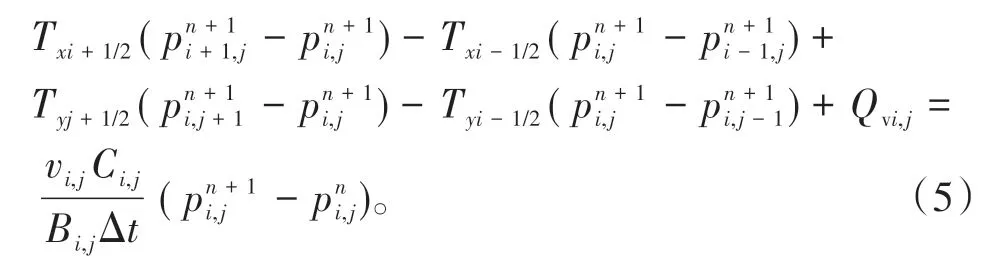
根据模型及初始条件，对该模型的边界条件、转向裂缝及传导系数进行处理，便可以计算出预测的产量。

2 实例应用

依据转向压裂产量预测及因素分析，利用Visual Basic 6.0 及Matlab 2014（a）研制相应的模拟软件。选取克拉玛依油田X 井进行模拟，X 井目标层埋藏深度为2 053.5 m，有效厚度为17.5 m；孔隙度为17.65%，渗透率为0.25 mD；地层温度为62.3 ℃，地层压力为14.2 MPa；施工排量为3.5 m3/min，前置液体积分数为40.4%，总液量为255.9 m3，总砂量为60 m3，平均砂比为21.6%。

X 井经过转向压裂后，一共形成7 条裂缝（图2），裂缝1为主裂缝，裂缝2—裂缝7为转向裂缝。主裂缝长度为170.9 m，导流能力为21 D·cm；裂缝2和裂缝7长度为49.2 m，裂缝3和裂缝5长度为56.0 m，裂缝4和裂缝6长度为10.1 m。X井在转向压裂前平均产油量为2.00 m3/d，经过转向压裂后平均产油量为12.68 m3/d，转向压裂后产油量比过去常规压裂井压后产油量提高5.3倍。将裂缝信息输入转向压裂产量预测软件，经过计算预测产油量为12.44 m3/d，实际产油量为13.75 m3/d，相对误差为9.5%。

图2 克拉玛依油田X井裂缝局部网格加密Fig.2.Local grid refinement in Well X of Karamay oilfield

3 产能影响因素

3.1 储集层渗透率

储集层渗透率是影响转向压裂开发井增产效果的主要因素之一。渗透率对产量的影响较大，需要对其进行敏感性分析。利用X 井的参数，固定其他参数不变，初次人工裂缝导流能力为30 D·cm，分支裂缝导流能力为20 D·cm，转向裂缝半长为60 m。针对渗透率为0.1 mD、0.5 mD、1.5 mD、2.5 mD、3.5 mD 和5.0 mD 的储集层进行模拟（图3）。由模拟结果可知，日产油量与累计产油量都随着储集层渗透率的增加而增加，储集层渗透率越高，初始日产油量越高，但产量递减速度都很快，在生产250 d 后都趋于平稳（图3a）。同时，在对渗透率进行敏感性分析时，也考虑了随着生产时间的增加，储集层渗透率对转向压裂后增产效果的影响。当储集层渗透率较小时，累计产油量增幅明显，当储集层渗透率达到2.5 mD 后，整体生产井的产油量增幅并不明显（图3b）。综上所述，转向压裂对储集层渗透率较低的生产井的改造具有良好的效果。

图3 克拉玛依油田X井不同渗透率产油量模拟Fig.3.Oil production simulation at different permeability in Well X of Karamay oilfield

3.2 转向裂缝导流能力

图4 克拉玛依油田X井不同裂缝导流能力组合产油量模拟Fig.4.Oil production simulation at different steering fracture conductivity in Well X of Karamay oilfield

利用X 井的参数，保持其他参数不变，储集层渗透率为1.5 mD，转向裂缝半长为60 m，设置模拟不同的初次人工裂缝和分支裂缝导流能力组合（图4）。模拟结果表明，裂缝导流能力组合不同，日产油量曲线在初值上差别较大，递减速度都很快，200 d后趋于平稳（图4a）。在生产的前期，较高导流能力组合的生产井的产油量增幅比低导流能力组合的生产井的产油量增幅要高很多；但在生产后期，高导流能力组合并不能使生产井维持较高的产油量，后期产油量增幅减小（图4b）。初次人工裂缝的导流能力能够维持更好地效果，且无须很高的分支裂缝导流能力。

3.3 转向裂缝长度

对转向裂缝长度对产油量的影响进行分析，利用X 井的参数，固定其他参数不变，储集层渗透率为1.5 mD，初次人工裂缝导流能力为30 D·cm，分支裂缝导流能力为20 D·cm，初次人工裂缝长度为170.9 m，设置模拟转向裂缝7 的长度分别为20 m、40 m、60 m和80 m（图5）。由模拟结果可知，日产油量与累计产油量随着转向裂缝长度的增加而增加。初期各条件下的日产油量相差不大，递减速度快，都呈直线递减，250 d 后几乎重合。与不转向压裂井相比，转向裂缝长度变长之后，可以扩大泄油面积，能达到有效增产的目的。转向裂缝越长，日产油量越高，但随着开发时间的增加，累计产油量增长变缓。

图5 克拉玛依油田X井转向裂缝不同缝长产油量模拟Fig.5.Oil production simulation at different steering fracture lengths in Well X of Karamay oilfield

4 结论

（1）本文根据转向压裂形成的转向裂缝进行精细描述，在坐标系中确定转向裂缝的分布位置、长度和角度。利用局部网格加密技术及数值模拟方法对产能进行预测，并对产能影响因素进行分析。

（2）依据转向压裂产油量预测及影响因素分析，自主研制相应的模拟软件，并进行现场应用。X 井在转向压裂前平均产油量为2.00 m3/d，经过转向压裂后平均产油量为12.68 m3/d，比常规压裂产油量提高5.3 倍。

（3）对产能影响因素进行敏感性分析得出：产油量随着渗透率的增加而增加，转向压裂对储集层渗透率较低的生产井的改造具有良好的效果；产油量随着裂缝导流能力的增加而增加，初次人工裂缝的导流能力能够维持更好的效果，且不需要很高的分支裂缝导流能力；与不转向压裂井相比，转向压裂后能有效增产，且转向裂缝长度越长，日产油量和累计产油量越高。

符号注释

B——体积系数；

C——压缩系数；

D——从某一基准面算起的垂直方向的深度，m；

g——重力加速度，m/s2；

k——储集层的渗透率，m2；

kx(x,y)——（x，y）处x方向的渗透率，m2；

ky(x,y)——（x，y）处y方向的渗透率，m2；

Lx——储集层在x方向的长度，m；

Ly——储集层在y方向的长度，m；

p——压力，Pa；

pi——原始地层压力，Pa；

q——储集层条件下单位体积岩石内注入或者采出的质量流量，kg/s；

qv——地面标准状况下单位体积岩石中注入或者采出的体积流量，m3/s；

Qvi，j——网格（i，j）的源汇项；

t——流体流动时间，s；

Txi±1/2——x方向的传导系数；

Tyi±1/2——y方向的传导系数；

vi，j——网格（i，j）的孔隙体积；

ρ——流体密度，kg/m3；

μ——流体黏度，Pa·s；

φ——储集层孔隙度；

Δxi——x方向第i网格宽度，m；

Δyj——y方向第j网格宽度，m。